基于土水特征曲线硫酸盐渍土渗透吸力试验研究

毛雪松，张腾达，刘飞飞，李颖颖

(长安大学 公路学院，陕西 西安 710000)

土水特征曲线是研究非饱和土力学性质的重要工具，主要表征非饱和土中体积含水率，或重力含水率，或饱和度和土中吸力的关系[1].非饱和土中的吸力由基质吸力和渗透吸力(或称溶质吸力)两部分组成，两者之和称为总吸力[2-3].对土水特征线曲的研究最早见于农业土壤学和土壤物理学[4].孙德安等[5]采用滤纸法和压力板法分析了氯盐渍土中含盐量对基质吸力和渗透吸力的影响，发现含盐量对基质吸力的影响较小而对渗透吸力的影响较大，但没有通过拟合工具得出含盐量与渗透吸力的具体关系式.于沉香等[6]利用Ku-pF 非饱和导水率仪测试了不同干密度状态下盐渍土试样的土水特征曲线发现渗透吸力的存在使土水特征曲线转化阶段变的平缓，同时发现干密度随土水特征曲线的影响较大.陈东霞[7]等采用滤纸法测定基质吸力，并且利用数学模型对所获取的含水量和吸力值进行拟合，从而得到土水特征曲线.根据已有研究发现，几乎没有学者对含盐量与渗透吸力的关系进行深入研究，土水特征曲线研究中多考虑干密度、含水率和含盐量与基质吸力的关系[8].同时以往研究多集中于氯盐渍土和碳酸盐渍土，或者笼统的仅说明对盐渍土的研究，具体针对硫酸盐渍土的研究较少.由于硫酸盐渍土的土水特征曲线受多种复杂因素的影响，目前仍不能定量的推导出体积含水率和总吸力值以及和含盐量与渗透吸力的关系，故本文现采用滤纸法[9]测定不同含盐量硫酸盐渍土土体的吸力值，从而绘制不同含盐量条件下的土水特征曲线，并绘制渗透吸力与含盐量、体积含水率的三维曲面图，来揭示一定范围内体积含水率与总吸力的关系以及含盐量、体积含水率对渗透吸力的影响规律.

1 滤纸法测试试验

1.1 试验原理

硫酸盐渍土中除了水分自身迁移引起土体力学性能变化外，盐渍土中所含的盐分也会随着水分发生迁移.水分迁移的动力来源于毛细管作用、薄膜水迁移、吸附-薄膜水迁移和土水势作用，尤其受到土水势中多种势能的影响.本实验主要研究基质势和溶质势的影响.滤纸法主要遵循热力学平衡原理，土体发生水分迁移时，盖在上面的滤纸也将产生迁移现象，直至水分迁移稳定后，滤纸和土体的吸力值相等，但两者的含水量并不相同，从而间接确定土样的吸力值.通过率定试验获取所用滤纸的率定曲线，经过计算得到滤纸的吸力值，并最终获取土体的总吸力值.本试验采用英国whatman42号无灰级定量滤纸，直径为55 mm和47 mm[10]，率定公式如公式(1)所示.根据滤纸与土体接触程度的不同分为接触法和非接触法，本文采用滤纸法[11]中的非接触法来测定硫酸盐渍土的总吸力.

(1)

式中：s为土体的总吸力值，kPa；wf为滤纸的质量含水率，%.

1.2 试验样品

试验所需土样采取人工挖土的方法，间隔相应距离各挖深50 m后在土坑中取圆柱形土柱20个，为保证试验质量，取样后立即用塑料薄膜密封放置铝筒内，如图1所示.在室内采用“干盐加湿土法[12]，模仿大多学者的硫酸盐配制方法，自行完成硫酸盐渍土的配制，同时完成水分盐分标定.土体的基本物理性质指标，如表1所示.

表1 土样的基本物理特性指标

图1 取土试样Fig.1 Soil sample

1.3 试验方法及步骤

实验采用土样含盐量分别为0%、0.4%、0.8%、1.2%和1.6%，每组质量含水率分别为5%、8%、12%、15%和18%.首先根据上述范围配制25组不同含盐量不同含水率的土样，圆形土柱的高度和直径都是50 mm，每组配制6个试件，配制过程应尽量均匀，以致完成后土柱各个方向都均匀平整.下一步将烘干后的滤纸进行称量计数，然后将滤纸与土体非接触放置.将处置好的土柱用保鲜膜密封，在恒温恒湿箱中放置7天，以便于滤纸和土柱的含水率达到平衡状态.平衡结束后，快速取出滤纸，将滤纸放在洁净干燥的铝盒中称量，记录下铝盒和滤纸的质量.然后把放有滤纸的铝盒标记好后放入烘箱中，温度设置为105 ℃，烘干时长为8 h.然后将烘干后的滤纸快速称量，滤纸称重的操作过程要求在5 s内完成，快速记录称量的滤纸质量.这个过程完成后在试验土柱中取出适量土样放置烘箱内进行烘干，测定其质量含水率.每一组试验都同上述步骤一样，重复该试验过程即可，此处不做赘述.

2 硫酸盐渍土总吸力与体积含水率的关系研究

2.1 硫酸盐渍土的土水特征曲线

通过试验获取的数据，带入已知的率定公式，计算土体总吸力值.为了更加直观而准确地反映土体中体积含水率和总吸力的关系，绘制不同硫酸盐含量条件下土体的总吸力与体积含水率变化关系曲线，如图2.

图2 不同硫酸盐含量的盐渍土土水特征曲线Fig.2 Soil water characteristic curve of saline soil with different sulfate content

由图1可知，同经典的土水特征曲线相比，该试验曲线符合其大致趋势，主要特点如下：

(1)在一定的范围内，所有试样的总吸力值随体积含水率的增加而不断减少.(2)同一般土体的土水特征曲线相比，该土水特征曲线在体积含水率为10%～20%期间有明显的凹陷，原因主要是盐分的浓度在饱和前以先快后慢的速率增加，而基质吸力是呈线性变化，两者重叠便出现明显的突变现象.(3)不同含盐量的SWCC曲线分布有明显的差异性，整体上发现，含盐量小的试样曲线始终处于含盐量大的试样曲线下方，说明在土中总吸力一定时，含盐量大的试样体积含水率也较大，同时对水分的吸持能力也较强.即含盐量越大试样的持水能力也越强.含盐量0%的试样总吸力值在整个过程中均最小，即说明素土的总吸力值明显小于盐渍土.(4)各试样土水特征曲线在20%含水率之前曲线较陡，后面则趋于平缓，直至同种同样不同含盐量的体积含水率趋于一致出现交叉现象，说明在含水率较小时，总吸力对体积含水率的变化的敏感程度明显高于体积含水率较高时.交叉重合现象大致出现在吸力值在10 kPa及以下，说明在该吸力值条件下含盐量对试样的持水能力几乎没有影响.

2.2 土水特征曲线拟合分析

以往研究土水特征曲线拟合的数学模型Van Genuchten[13]，Fredlund and Xing[14]以及 Garder[15]大多针对非饱和土类这一较大范围，但硫酸盐渍土由于不同盐分的掺入属于特殊土.本文采用专业函数绘图软件Origin对所测定的数据进行曲线拟合分析，旨在得到硫酸盐渍土中体积含水率和总吸力值的关系.试拟合多次后发现函数类型Exponential中的Exp2PMod1函数拟合效果最好.数据拟合后得到在一定的含盐量条件下，土体体积含水率和总吸力呈现指数关系，且拟合后的相关系数均大于0.98.这样，不同含盐量的硫酸盐渍土的基质吸力和体积含水率有一个共同的关系式：s=Ae-Bθw，如表2所示.这个公式可以帮助对硫酸盐渍土土水特征曲线预测模型的建立.

表2 基质吸力和体积含水率关系的拟合方程

3 渗透吸力与含盐量、体积含水率关系的研究

非饱和土中的土水势由重力势、压力势、基质势、溶质势和温度势五部分组成.本试验中各组试验是在同一的环境下进行的，则土体重力势和温度势可以不考虑，并且以同一个面为参考，同时盐渍土属非饱和土，压力势为零.因而该试验中硫酸盐渍土土水势仅有基质势与溶质势.不同含盐量硫酸盐渍土的吸力值减去素土吸力值，即得到硫酸盐渍土含盐量与渗透吸力关系图，如图3.

根据土中曲线的走向趋势，可以看出如下特点：(1)在一定范围内同一含水率条件下渗透吸力随含盐量的增加而不断增加，呈正比例关系.由前述可知，此时渗透吸力的数值为相同含水率下盐渍土与素土的吸力差值，所以导致渗透吸力增加的主要原因是因为含盐量的增加.并且含盐量越大，渗透吸力也越大.这种现象的解释是因为盐分的加入，土体中的水分与盐分融合成盐溶液，盐分越大，溶质含量越大，浓度增加，随之土体中的孔隙水压力降低，最终表现为渗透吸力值不断增加.

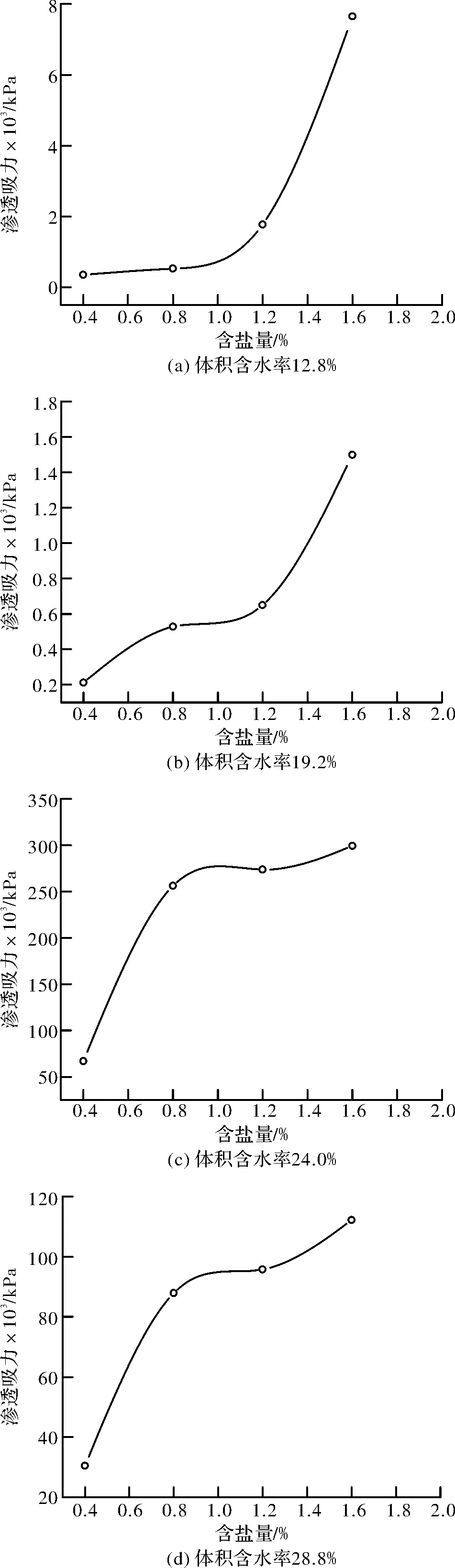
图3 含盐量与渗透吸力关系曲线图Fig.3 salinity and osmotic suction

(2)从曲线的变化可以看出，在含盐量小于1.2%的初始阶段，渗透吸力增长的速度较快，当含盐量大于等于1.2%时，渗透吸力的增长速度有所减慢，曲线相对更加平缓.说明试样渗透吸力在含盐量1.2%时发生突变，注意到在渗透吸力与含盐量关系图中该突起尤其明显，说明突起的形成与渗透吸力有很大的关系.硫酸盐渍土中盐分浓度在饱和前随着水分和盐分迁移呈先快后慢的速度增长，溶质含量的变化即反应在渗透吸力的变化上.同时注意到在随着含盐量的继续增加，渗透吸力并没有持续增加而是趋于一个稳定值，这是因为土中自由水的含量有限，当土中硫酸盐全部变成盐溶液后，随后即使再加大盐分掺入量，渗透吸力并不能保持持续增长的趋势.

研究吸力时，体积含水率是其宏观的主要影响因素，含盐量的增加对渗透吸力[16]产生较大的影响，故对渗透吸力与含盐量、体积含水率的关系建立显得十分必要.根据图1中数据，体积含水率取值0～30%，含盐量取值0～1.6%.由于没有经验模型作为参考，现依托MATLAB[17]拟建立“渗透吸力=f(含盐量，体积含水率)模型，采用cftool工具箱进行拟合分析.首先导入数据初建三维曲面图(图4)；然后选择Interpolant执行Biharmonic(V4)算法对图形进行曲面的圆滑处理(图5)，最后选择Polynomial算法，多次试拟合后，确定拟合函数z=f(x,y)，即渗透吸力=f(含盐量，体积含水率)的三维曲面图(图6).

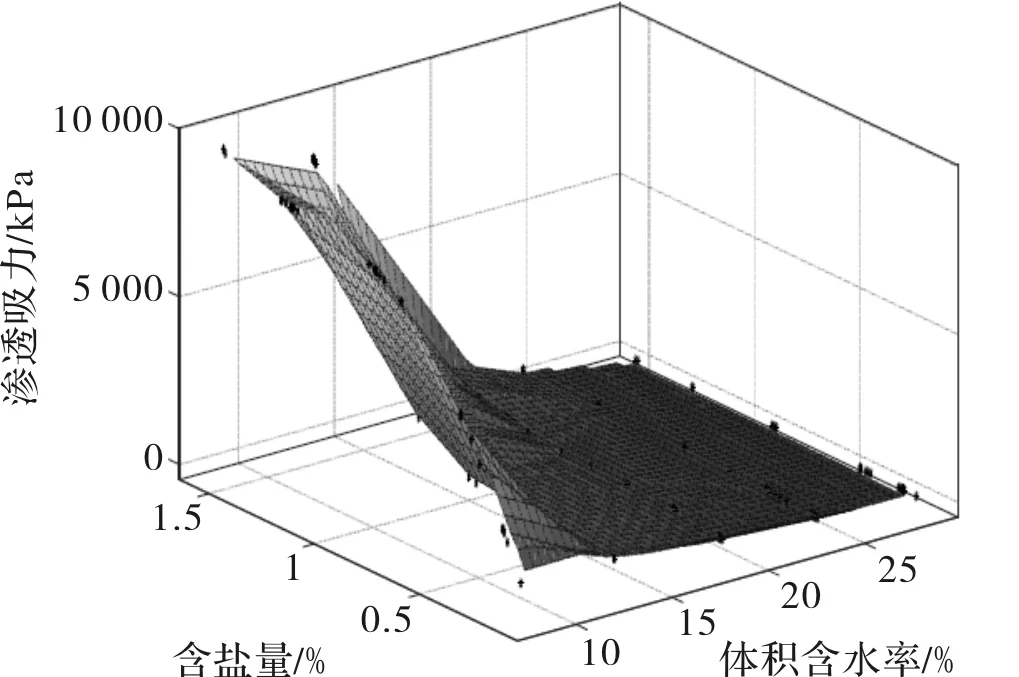
图4 渗透吸力与含盐量、体积含水率的双变量关系Fig.4 Bivariate relationship between osmotic suction and salinity and volumetric moisture content

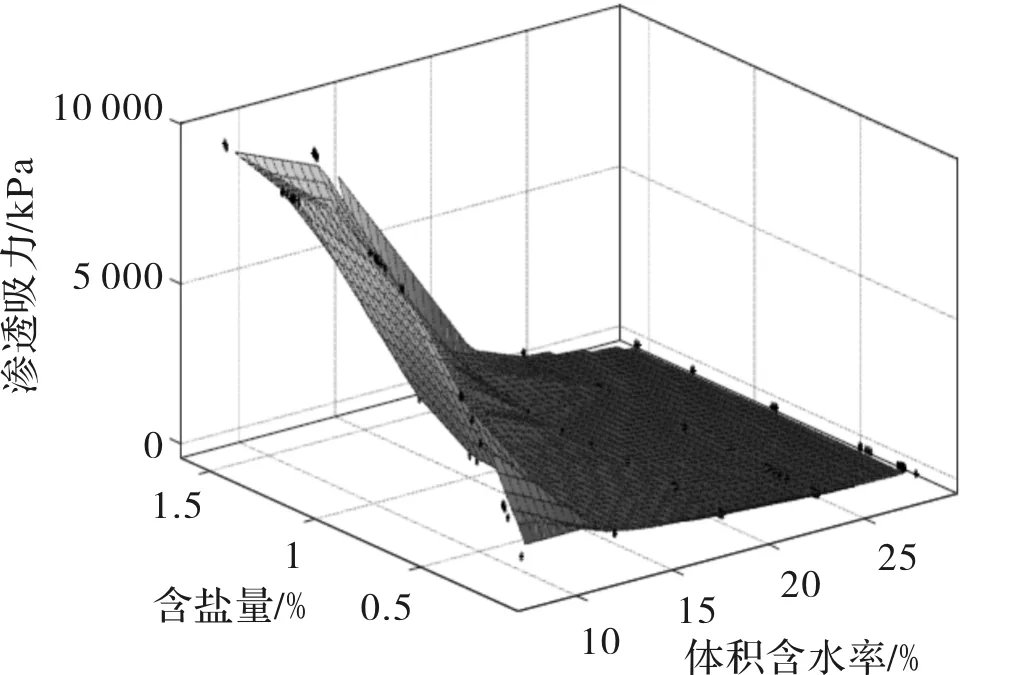
图5 渗透吸力与含盐量、体积含水率圆滑处理Fig. 5 Osmotic suction and salinity , volumetric moisture content smoothing

图6 渗透吸力与含盐量、体积含水率的三维曲面图Fig.6 Three-dimensional surface map of osmotic suction and salinity and volumetric moisture content

拟合函数的确定系数R-square和Adjusted R-square值均在0.95以上，从而拟合的曲面方程效果较好，可以反映三者之间的关系.因此选用linear model poly 21作为“渗透吸力=f(含盐量，体积含水率)”的模型，表达式为见公式(2)：

f(x,y) = 583.3-1 953x+776.1y+
1 077x2-1 059xy

(2)

4 结论

(1)使用滤纸法测定硫酸盐渍土总吸力和体积含水率，研究发现，硫酸盐渍土的土水特征曲线符合非饱和土经典土水特征曲线，但同时由于盐分的加入表现出了不同之处，即硫酸盐渍土土水特征曲线有明显的凹陷现象.

(2)通过对数据的拟合分析发现，一定范围内，硫酸盐渍土体积含水率和总吸力之间呈指数关系：s=Ae-Bθw.这为以后硫酸盐渍土数学模型的预测提供借鉴作用.

(3)根据计算机语言MATLAB的拟合结果表明，在一定的范围内，硫酸盐渍土渗透吸力与含盐量、体积含水率呈幂函数关系.拟合结果R2在0.95以上，拟合效果较好.拟合模型确定为linear model poly 21.

(4)同时研究发现，在一定的含水率条件下，含盐量的变化对渗透吸力的影响较大，对基质吸力的影响较小.