基于Morlet小波的辽河径流量变化及其成因分析

冯禹昊, 朱江玲

(北京大学 城市与环境科学学院, 北京 100871)

在全球人口增长和气候变化背景下，水资源的短缺和时空分布不均已经成为人类经济社会发展的重要挑战。因此，通过气候因子对河川径流量进行合理预测可以帮助实现对水资源的统筹规划和集约利用，具有十分重要的现实意义[1]。然而很多研究表明，河川径流量和各种气候因子受到众多自然和人为干扰过程影响，变化规律极端复杂且因素间存在着多时间尺度的非线性响应。因此必须引入新的适用于复杂时间序列数据的研究方法。小波分析作为多时间尺度分析的理想工具，已经广泛地应用于河川径流量和气候因子相关关系的研究中：陈效逑等[2]基于小波互相关分析方法分区域地讨论了各气候因子对黄河径流量变化的驱动机制，揭示了不同时间尺度上年均温和蒸发量对径流量的负向影响以及年降水量对径流量的正向影响；凌红波等[3]通过小波交叉谱识别了天山山区年均温、年降水量与区域径流量的相关关系。不同于黄河流域的是，干旱、半干旱区内陆河径流量与年均温、年降水量均存在着显著的正相关关系；此外，类似的研究还在玛纳斯河[4]、开都河[5]、渭河[6]、嘉陵江[7]、雅鲁藏布江[8]等流域开展。

然而，尽管这种以小波分析及小波互相关为主体的研究范式已经形成，并被应用于很多流域，其过程仍然有以下两项亟待改善之处：其一，小波尺度与真实时间尺度的混淆。两者之间的转换与所用小波的中心频率以及数据的采样频率密切相关。但很多研究[9-11]都没有阐明两者间的变换关系，从而导致了错用；其二，各气候因子间通常存在显著的相关关系，很多研究[2,12]在讨论单一因子的影响时并未排除其他因子的作用。

基于此，本研究将在规范使用小波分析方法的基础上，引入偏相关系数对小波互相关结果进行校正，以识别年均温、年降水量、蒸发量3个气候因子对径流量的独立影响，以期揭示引发径流量年际变化的主要因素。此外，本文还将研究区域设置在辽河流域，以期探究半湿润季风区河川径流量间对各气候因子的响应。

1 流域概况

辽河发源于河北省平泉县，全长1 345 km，干流长516 km，系中国七大河流之一。辽河流域位于40.5°—45.2°N，116.8°—125.5°E，覆盖河北、内蒙古、吉林以及辽宁部分地区，流域面积21.9万km2。辽河水系分布及流域内58个气象观测站的位置如图1所示。流域大部分地区属半湿润半干旱气候，年均温为5～9℃，年降水量为400～750 mm，径流量数据及各气候因子(取各站平均值)的年际变化情况如图2所示。

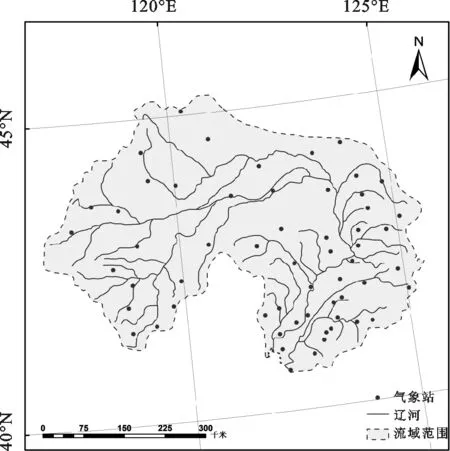
图1研究区域及气象站分布

图21956-2009年径流量及气候因子年际变化

流域多年平均径流量为27.8亿m3，1956—2009年总体上呈现出减少的趋势。从5年滑动平均值来看，流域径流量存在明显的波动特征，1956—1966年、1984—1996年为径流量较大的两个时段，平均年径流量达41.1亿m3；1967—1983年、1997—2009年径流量较少，平均值为16.6亿m3。流域多年平均气温为6.8℃。在全球气候变化背景下，年均温在研究时段内出现了显著的增长，增速约为0.03℃/a。年降水量也表现出周期性变化特征，且与径流量变化有较强的一致性：1956—1964年、1983—1995年降水量较多；1965—1982年、1996—2009年降水量较少。年蒸发量仅在1956年、2002—2009年出现了较小值，在其他时段并无显著的单调或周期性变化特征。

2 研究方法

2.1 数据预处理

小波系数是小波函数在特定尺度和相位下与时间序列数据间的相关性度量。从统计学的角度来看，样本量是进行两个相关系数大小比较的关键因素[13]。因此，为了确保小波系数间的可比性，研究中首先应将原始的时间序列数据向两端进行充分地拓展，以消除序列两端积分范围跨度不同造成的影响。本研究使用对称变换的方法向外增加资料，并在完成系数计算后，从中提取原始资料对应时段的小波系数值[14-15],详细方法如公式(1)—(3)所示：

f(1),f(2),…，f(n)

(1)

f(-i)=f(i+1) (i=0,1,…,n-1)

(2)

f(i+n)=f(n+1-i) (i=0,1,…,n-1)

(3)

式中：公式(1)为原始资料的抽象表示；n为样本量，公式(2)，(3)分别为向前和向后延伸n点的计算方法。

2.2 小波分析

小波变换通过伸缩和平移小波函数实现对时间序列数据的多时间尺度分解，从而得到原始信号在不同尺度上的周期性变化特征。具体地，连续小波变换可以定义为[16]：

(4)

式中：x(t)原始信号；ψ(t)为小波母函数；a为尺度因子；τ为位移因子；*表示共轭；积分结果W(a,τ)即为小波系数，反映了尺度为a，位移τ为时的小波函数与原始信号间相关性的强弱。

在众多的小波母函数中，由于复Morlet小波能够消除用实小波变换系数作为判据产生的虚假振荡且不具有正交性，所以它被很多地球物理过程的分析所采用[17]。复Morlet小波的母小波可以由公式(5)表示[18]：

(5)

式中：fb为小波带宽；fc为小波中心频率；i为虚数符号。在本研究中，为便于进行小波尺度与真实尺度的变换取fc为1，同时根据小波变换效果确定较优的带宽取值为1.5。

小波尺度a不等同于真实的时间尺度，两者的对应关系可以由公式(6)确定[19]：

fa=(fc/a)·Ta

(6)

式中：fc为小波中心频率；Ta为采样的时间间隔；fa为真实尺度的对应的频率，即真实尺度的倒数。在本研究中，由于采用的是年度数据，所以Ta值为1；又有fc被定为1，因此小波尺度在数值上等于真实时间尺度。

小波方差反映了特定时间尺度下信号的平均能量[20]，小波方差越大，信号在对应尺度上的周期性特征就越显著。其值可由公式(7)计算：

(7)

式中：|W(a,τ)|是尺度为a，位移因子为τ时的小波系数绝对值，对于复系数来说则是其模长；N为a尺度下求得的小波系数总数。

2.3 小波互相关分析

小波互相关分析能定量描述两个非平稳时间序列之间在某特定尺度上的相关关系，是基于小波变换系数进行多时间尺度驱动因子判定和评估的理想工具。由于小波系数实部值就能够反映信号在不同时间尺度的周期变化及其在时间域中的分布，因此为了简化计算，本研究只提取了实部值进行序列互相关分析。桑燕芳等[21]提出了基于连续小波变换的互相关系数求解方法，根据本研究所用数据的特点可将该方法提炼为公式(8)—(9)：

Wcovxy(a,k)=Eb[Wx(a,b)Wy(a,b+k)]

(8)

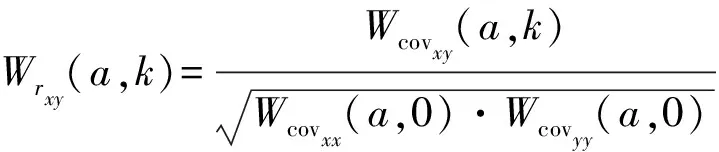
(9)

式中：Wx(a,b)表示序列x在时间尺度为a，时刻为b时的小波系数；Eb[ ]表示对括弧中的算式求关于b的期望；k为序列y对于x的时滞；公式(9)中互相关系数的计算在形式上与传统相关系数的计算相同。基于公式(9)：还可以对相同时滞k下的互相关系数求解加权平均值，计算小波互相关度[21]：

(10)

(11)

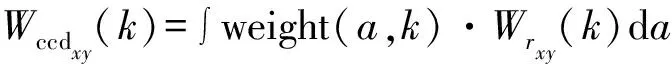
(12)

式中：Wccdxy(k)即为时滞k下序列x与y的互相关度；权重weight(a,k)实际上是固定时滞下的互相关系数平方占比。

与传统的二元相关系数类似，当序列数据受多个因素同时影响时，小波互相关系数无法表示单一因素对序列数据的独立作用。因此，本研究仿照偏相关分析方法[13]，在公式(9)的基础上定义小波偏相关系数如下：

(13)

近年来，红枫家政公司贯彻落实《商务部关于加快居民生活服务业线上线下融合创新发展的实施意见》，创新转变家政服务供给方式，积极向“互联网+”方向快速发展。2012年在绵阳成功建成“红枫家政信息化办公OA系统”，2015年底在成都市顺利开建“云尚家美好生活家政服务智能平台”。目前，红枫家政公司已基本实现了家政服务手段信息化，信息发布、自助下单、服务评价、纠纷处理等服务实现“一站式”在线提供，有效对接了家政服务的供需双方，促进了家政服务线上线下融合发展，提升了服务效率和水平。

(14)

式中：Wrxy_z(a)为a时间尺度下，固定序列z时，序列x与y之间的相关系数；基于公式(13)可以容易表达出涉及4个变量的偏相关系数，Wrxy_zw(a)表示固定序列z和w时，序列x与y之间的相关系数。值得注意的是，由于偏相关系数在计算过程中涉及全部二元相关系数，因此无法定义序列间的时滞关系，公式(13)与(14)的计算默认在k=0的条件下进行。

3 结果与分析

3.1 径流量与气候因子的多时间尺度特征

由图3可知，辽河流域径流量表现为以10 a和36 a为主周期的年代际变化，其中36 a尺度上小波系数等值线闭合值较高，具有全域性特征。根据公式(4)—(5)，Morlet小波函数关于t=τ呈轴对称，且在该处取得最大正值。因此，小波系数为正说明原始信号与小波函数的形态相似，在相同尺度，t=τ处取得较大值，在本例中即为径流量较多的时刻。小波系数过程线(图3C)是小波系数矩阵(图3A)在主周期处的横向剖面，因而可以反映流域径流量的丰枯变化情况。从10 a尺度上看，1959—1962年、1968—1973年、1979—1983年、1989—1993年、1999—2003年、2008—2009年为负位相，径流量较少为枯水期，其余年份是正位相为丰水期；从36 a尺度上看，1956—1965年、1984—2000年为径流量较多的年份。综合上述结果可知，尽管存在小幅度的短周期波动，辽河目前还处在径流量较少的年份且这种状态将持续到2020年前后。

图4展示了辽河流域年均温的多时间尺度特征。小波方差的计算结果(图4B)表明年均温存在长达47 a的周期性变化，考虑到研究涉及的时间跨度只有54 a，这一较长的周期实际上反映了年均温在全时间域的递增趋势。此外，在4～14 a尺度间，小波方差出现了很多局部最大值，提取其中最大的14 a尺度绘制小波系数过程线(图4C)可以发现小波系数的绝对值逐渐减小，这表明14 a周期随着时间的推移逐渐消失。转而观察小波系数矩阵(图4A)可知，取代14 a周期的是7～8 a周期性变化，但这种变化也在2000年前后消失，取代其的最新周期长度为4～5 a。周期长度的逐渐缩短表明极端气候出现的频率增加，这与近年来的实际观测相符[22]。

图3辽河流域径流量小波分析结果

流域年降水量与径流量有相似的多时间尺度特征，均存在以10 a和36 a为主周期的年代际变化(图5B,5C)。不仅如此，两者的小波系数矩阵也有相似的分布模式(图3A,5A)，因此可以认为流域降水量是径流量年际变化的重要影响因子。降水量的长周期变化体现了小波分析方法对时间序列数据总体趋势的响应，而短周期变化则与由某些周期性的自然干扰过程调控。很多研究结果表明降水量以10 a为周期的变化与太阳活动密切相关[23-24]。

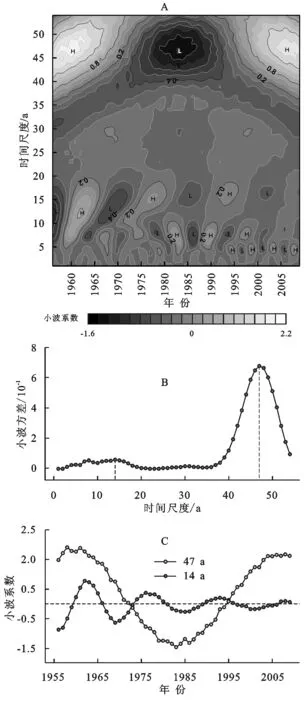
图4辽河流域年均温小波分析结果

与其他气候因子相比，蒸发量的周期性特征较为模糊，在15～40 a范围内其小波方差值均处于较高水平(图6B)。取18 a，29 a两个极大值点绘制小波过程线(图6C)可以发现，两个尺度上小波系数的绝对值大小近似相同且波形间不存在明显的同步或包含关系，因此可以认为蒸发量的年际变化是一种随机波动，无显著的周期变化规律。

图5辽河流域年降水量小波分析结果

3.2 径流量年际变化驱动因子分析

不同时间尺度下，辽河流域径流量与气候因子及各气候因子间的小波互相关分析结果如图7所示。其中，年径流量与年均温在1～35 a尺度上以负相关为主，最小值出现在7 a处为-0.84，然而在较大尺度上两者却表现为正相关，相关系数值在50 a尺度处达到了最大值0.81。根据公式(10)—(12)计算得到的小波互相关度为0.202 1，可以认为两序列总体上呈正相关关系；年径流量与年降水量在几乎全部时间尺度(1～51 a)上呈正相关，但相关系数在48 a之后出现了迅速下降并最终转为负值。高达0.874 3的小波互相关度表明两序列在总体上呈显著的正相关关系，即径流量的减少系年降水量的减少所致(图2A,2C)；年径流量与年蒸发量间的小波互相关系数随时间尺度的增大出现了明显的正负交替：1～11 a，14～26 a，49～54 a为负相关区间；12～13 a，27～48 a为正相关区间。这样的交替变化使得小波互相关度的计算结果接近于0(-0.158 8)，两序列呈微弱的负相关关系。

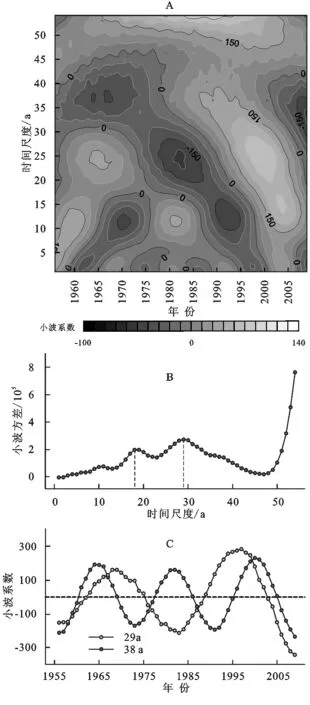
图6辽河流域年蒸发量小波分析结果

一般认为，在以自然降水为主要河流水源的地区，年均温与蒸发量对径流量有负向影响，降水量对径流量有正向影响[25-26]。然而，小波互相关的分析结果却得到了与之相矛盾的结论：其一，径流量与年均温的小波互相关系数在较大时间尺度上出现正值，导致互相关系数的加权平均值为正，即两者在总体上呈正相关关系；其二，径流量与年降水量在较大尺度上呈负相关关系。上述矛盾在陈效逑等[2]对黄河流域径流量与气候因子的互相关分析中也有出现。究其原因，我们认为各气候因子间的相关关系影响了互相关分析结果。如图7所示，年均温与年降水量、年蒸发量均存在较强的正相关关系(相关系数分别为0.489 9，0.668 6)。因此，在分析单一气候因子对流域径流量的作用时，必须对这些相关关系进行处理和排除。为此，本研究引入了偏相关系数对小波互相关系数进行校正。

校正后的小波互相关分析结果如图8所示。图中的不显著域由参与互(偏)相关系数计算的样本量(54)、置信度水平(95%)决定，通过查询统计用表[13]可知，本例中互相关系数的不显著域为[-0.273,0.273]；偏相关系数的不显著域为[-0.379,0.379]。

在排除年降水量和蒸发量的影响后，年径流量与年均温在几乎全部时间尺度(除54 a)呈负相关或不显著相关关系(图8A)，系数加权平均值由校正前的0.202 1变为-0.650 3，两序列从总体上的正相关转变为负相关。此外，尽管偏相关系数的不显著域范围大于互相关系数，前者落入不显著域中的值个数却少于后者，这表明经偏相关处理后，时间序列数据在不同时间尺度上的特征得到增强，更能够反映气候因子对因变量真实且独立的影响。

经校正，年降水量在全部时间尺度上表现出对径流量的正向影响(图8B)。互相关系数在48 a尺度后的迅速转负得到了控制并表现为显著的正相关，虽然在固定年均温和年蒸发量后，系数加权平均值出现了微弱的下降(由0.874 3降至0.860 9)，但依旧可以认为辽河流域径流量的波动变化与年降水量密切相关，且两者间具有很强的正相关关系。

虽然经过校正后年蒸发量与径流量间的负相关关系得到加强(系数加权平均值由-0.158 8变为-0.450 5)，但由于系数值落入不显著域内的个数过多，因此不能认为蒸发量对径流量存在显著的负向影响(图8C)。同时，由于大尺度上两者偏相关系数为负，可以归因于年蒸发量在研究时段两端出现的较低值对大尺度小波系数的控制(图2)，因此应优先考虑较小时间尺度上的系数值。以径流量的较大主周期36 a为界，考察小尺度上偏相关系数值的分布，可以发现：正值与负值数量基本持平(分别为17个和19个)，在不显著域外的负值对正值在数量上也没有绝对的优势(分别为10个和5个)。综上，我们认为年蒸发量与径流量的波动周期不存在显著的相关关系。

图7辽河流域径流量与气候因子及各气候因子间小波互相关分析结果

4 结 论

本研究综合利用小波分析、小波互相关与偏相关分析方法探究了辽河流域径流量、年均温、年降水量以及年蒸发量的多时间尺度特征及其相关关系。结论如下：(1) 1956—2009年，辽河流域径流量存在以10 a为主的短波动周期和以36 a为主的长波动周期；(2) 受极端气候出现频率增加的影响，流域年均温波动变化周期逐年缩短。此外，年降水量的周期性特征与径流量相似，存在以10 a和36 a为主周期的波动。年蒸发量不存在明显的周期变化规律；(3) 流域年均温的增加以及年降水量的减少是径流量减少的直接诱因。排除年均温影响时，年蒸发量与径流量之间不存在显著的相关关系，可以判定其为间接因素。

本研究通过引入偏相关系数更新了基于小波分析与小波互相关进行时间序列数据相关性研究的范式，得到了较已有方法更符合先验知识的结论，更好地解释了流域径流量年际变化的成因。研究所得的关于辽河流域径流量的周期性变化规律及其驱动因子的分析结果对流域水资源的管理和调度也有重要的参考意义。但同时需要指出的是，本研究还存在以下不足之处：(1) 研究仅考虑了气候因子对径流量的影响，没有考察人为因素对径流量的调控；(2) 研究仅给出了定性关系，没有深入分析各气候因子对径流量的贡献率；(3) 年蒸发量在研究时段两端的较低值对结论有较大的影响，因而需要使用时间跨度更大，更加精细的数据进行补充分析。上述不足之处需要在之后的研究工作中加以改善。

图8辽河流域径流量与各气候因子间小波互相关与偏相关系数比较