基于室内定位技术的智慧疏导系统设计
刘智恒
(西安市消防救援支队,陕西 西安 710003)
0 引言
现如今,城市化进程加快,大型人员密集场所越来越多,场所内高密度人群的出现频率大大增加。当发生火灾时,人群的流动往往被限制在有限空间内。由于大多数人员并不熟悉场所的内部环境,加之火灾烟气、热辐射等恶劣环境的影响,导致人群对疏散通道的选择从众化、盲目化,人员的疏散效率显著降低。疏散困难往往是导致踩踏事故和人员伤亡的主要原因,因此对发生火灾后进行快速、有效的疏散提出了更高要求。目前,智能疏导系统是根据探测火源位置,动态改变疏散指示标志的方向,结合消防广播引导人员进行安全疏散。智能疏导系统可帮助人员选取合理的疏散通道,避免人员进入火灾危险区域,提高疏散效率。但若在人员密集场所,智能疏导系统不能根据疏散通道的人员密度信息动态改变疏散指示标志的指向,人员潜意识选择自己熟悉的通道,并且智能疏导系统只能确定火灾发生时的区域人群疏散方向,不能结合个体(尤其两区域交界处人员)和现场情况对人员进行最佳路径推荐,这样极有可能造成单条通道过度拥挤,导致疏散效率降低,易导致踩踏事故的发生,因此有必要提高智能疏导系统的智慧化程度。李清泉等[1]最先提出了一种基于“时空拥挤度”的应急疏散路径优化方法,该方法能够为大型公共场所的人员疏散提供从建筑物内部经由路网离开危险区域的一个完整疏散路径方案。分析在疏散路径的分配过程中以最短路径为基础的疏散路径分配方案的拥堵情形,然后以缓解拥堵、减少疏散总时间为目标,设计疏散路径分配方案的优化方法。Mukherjee[2]提出了一种用于解决复杂环境下人员疏散的最短路径的算法模型。该算法为基于Dijkstra在复杂环境下的一种最优化路径算法模型,能有效解决复杂环境人员疏散问题,用于已知人员的具体位置[3]、数量、建筑的情况来预设疏散方案,不能用于流动性较大、人员具体位置不明确的场所疏散[4-10]。本文通过UWB室内定位技术,搭建智慧疏导系统设计框架。系统通过获取人员的实时位置、不同区域人员密度、火灾探测信息等,结合Dijkstra算法设计出疏导模型,通过对比不同疏散方向的疏散路径“权值”,确定人员的最佳疏散路径,并利用手机客户端的三维地图模型进行实时展示,以高效安全地引导人员进行疏散。
1 系统设计原理及方法
1.1 设计框架
本系统架构基于FengMap三维地图引擎、UWB室内定位技术、Spring-MVC设计模式,旨在结合各类现场实时信息,通过手机客户端为用户推荐一条符合用户当前位置的最佳疏散路径。系统实现框架如图1所示。
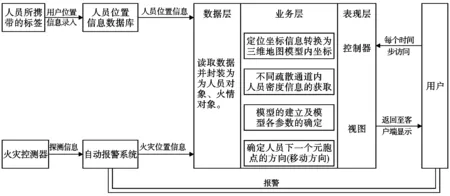
图1 智慧疏导系统设计框架
在图1中,系统首先根据场所的建筑施工图,建立基于三维室内地图的客户端软件,搭建室内定位基站,进行待定位人员信息的获取与校验。发生紧急情况时,用户打开客户端软件访问服务器,服务器端根据火灾报警位置信息确定火灾蔓延程度,结合人员位置信息、不同区域人员密度信息,确定人员的最佳疏散路线,通过可视化视图向用户进行实时展示。
1.2 数据获取
1.2.1 人员定位信息的获取
智慧疏导系统采取UWB(Ultra Wideband)定位技术获取所有人员位置信息,通过软件平台分析、计算所有位置信息并将信息反馈给用户。UWB技术是一种不用载波,利用纳秒至微秒级的非正弦窄波脉冲传输数据的无线通信技术,数据速率可达几十Mbps到几百Mbps。UWB室内定位技术抗干扰能力强、发射功率低、可全数字化实现,可以应用到静止或者移动的目标,提供十分精确的定位。
UWB室内定位系统原理如图2所示,标签发射极短的UWB脉冲信号,包含UWB天线阵列的传感器接收此信号,并根据信号到达时间差和到达角度计算出标签的精确位置。传感器按照蜂窝单元的组织形式布置,每个定位单元中,主传感器配合其他传感器工作,并负责与标签进行通信,可以根据需覆盖的范围进行附加传感器的添加。传感器可以通过以太网或无线局域网,将标签位置发送到定位引擎。定位引擎将数据进行综合,通过定位平台软件,实现可视化处理。
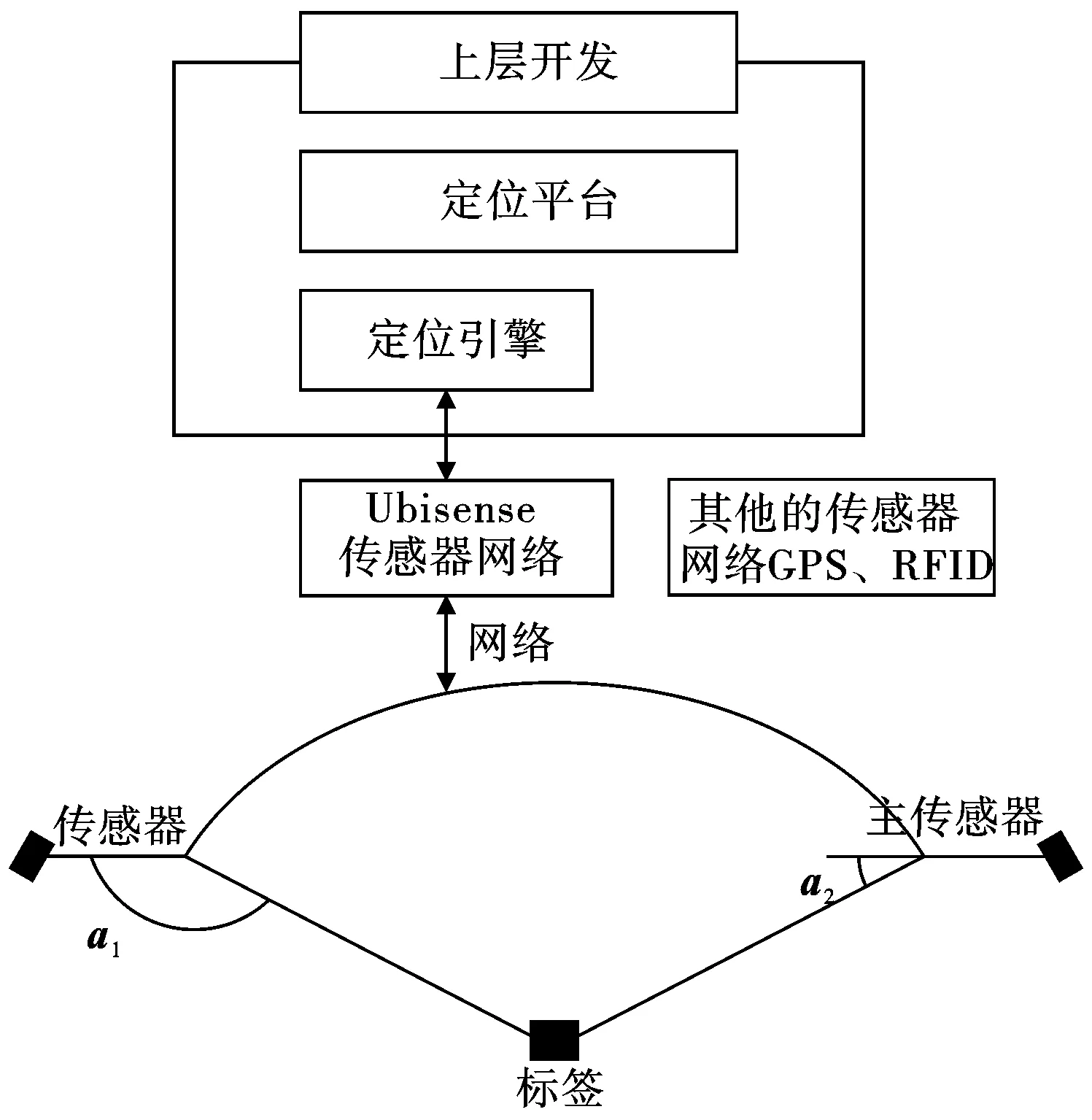
图2 UWB室内定位系统原理
1.2.2 火灾相关信息的获取
火灾相关信息获取的主要流程如图3所示,系统通过智能火灾探测技术,获取发出报警信号的火灾探测器地址,并根据地址信息从火灾报警系统数据库中获取与之绑定的火灾相关信息,如位置信息、可燃物类型、火灾荷载等。将获取的信息发往服务器端为智慧疏导模型提供数据基础。
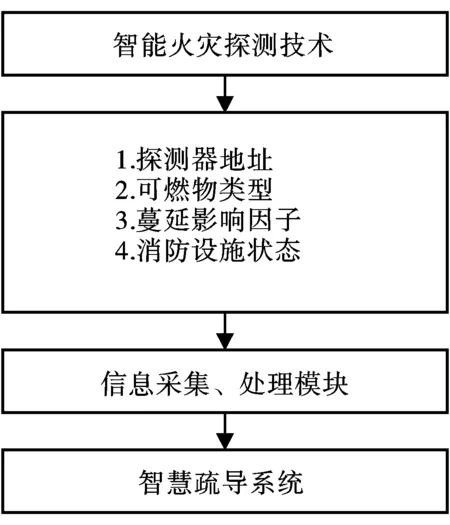
图3 火灾位置信息的获取流程
考虑到目前火灾探测器不能探测出可燃物类型,获取不到蔓延影响因素、烟气流动状态等,本文将可燃物类型、蔓延影响因子等信息与火灾探测器地址绑定,建立数据库表,提前在数据库表中录入绑定信息。这样,发生火灾时可以通过火灾探测器地址在数据库中查找到提前录入的绑定信息,为人员疏散提供数据支持。
2 智慧疏导系统疏散模型的开发
2.1 模型的初步建立
智慧疏导系统根据改进的单源最短路径Dijkstra算法建立人员疏散模型,确定最优疏散路径。系统模型的影响因素分为相对位置信息(Sij)、火灾排斥力(Fij)、人员密度信息(Fρij)、各个疏散通道的宽度(l)。模型引入转移概率和概率矩阵概念,每个位置设置为可以朝向8个方向疏散[11],如图4为Moore邻域所对应的邻域和转移概率矩阵。
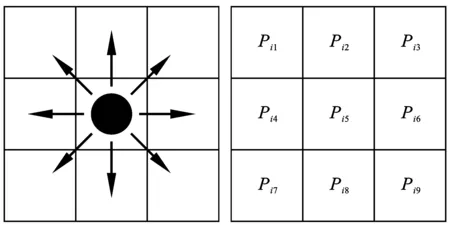
图4 Moore邻域和转移概率矩阵
转移概率的计算如下:
Pij=Nexp(ksSij+kfFij+kρFρij+kll)
(1)
N=[∑j∈Mexp(ksSij+kfFij+kρFρij+kll)]-1
(2)
式中,ks,kf,kρ,kl为各因素的影响系数;N为归一化因子,保证中心元胞向所有可能的目标格点转移的概率之和为1。
2.2 模型影响参数的量化过程
2.2.1 相对位置信息Sij
采用单源最短路径的Dijkstra算法确定Sij,假设人员起始位置为S,每个出口标记为G(j),将每条路径中的可中转点设为节点(用A,B,C等表示),R为路径权值,从起点开始使用算法,求出起点至集合点G(j)的最短路径集合,有障碍物或者起点到集合点之间无通路的,权值即为无穷大。图5为Dijkstra算法实现的简要流程图,Dijkstra算法的基本思路是对要求解的目标网络的节点与路径进行标记处理,首先将起始点S标记为已探知的节点T,再寻找与其相邻的其他节点与之的距离,标记最短路径,直至探寻到终点G,最后通过反向推算,将所有路径进行标记验证。图6为使用Dijkstra算法确定相对位置信息Sij,此处将路径长度设置为路径权值并通过Dijkstra算法求出最短路径。本文将最短路径的Sij值设置为最大值,设置最远路径Sij为0,通过迭代为其他路径的Sij进行赋值。
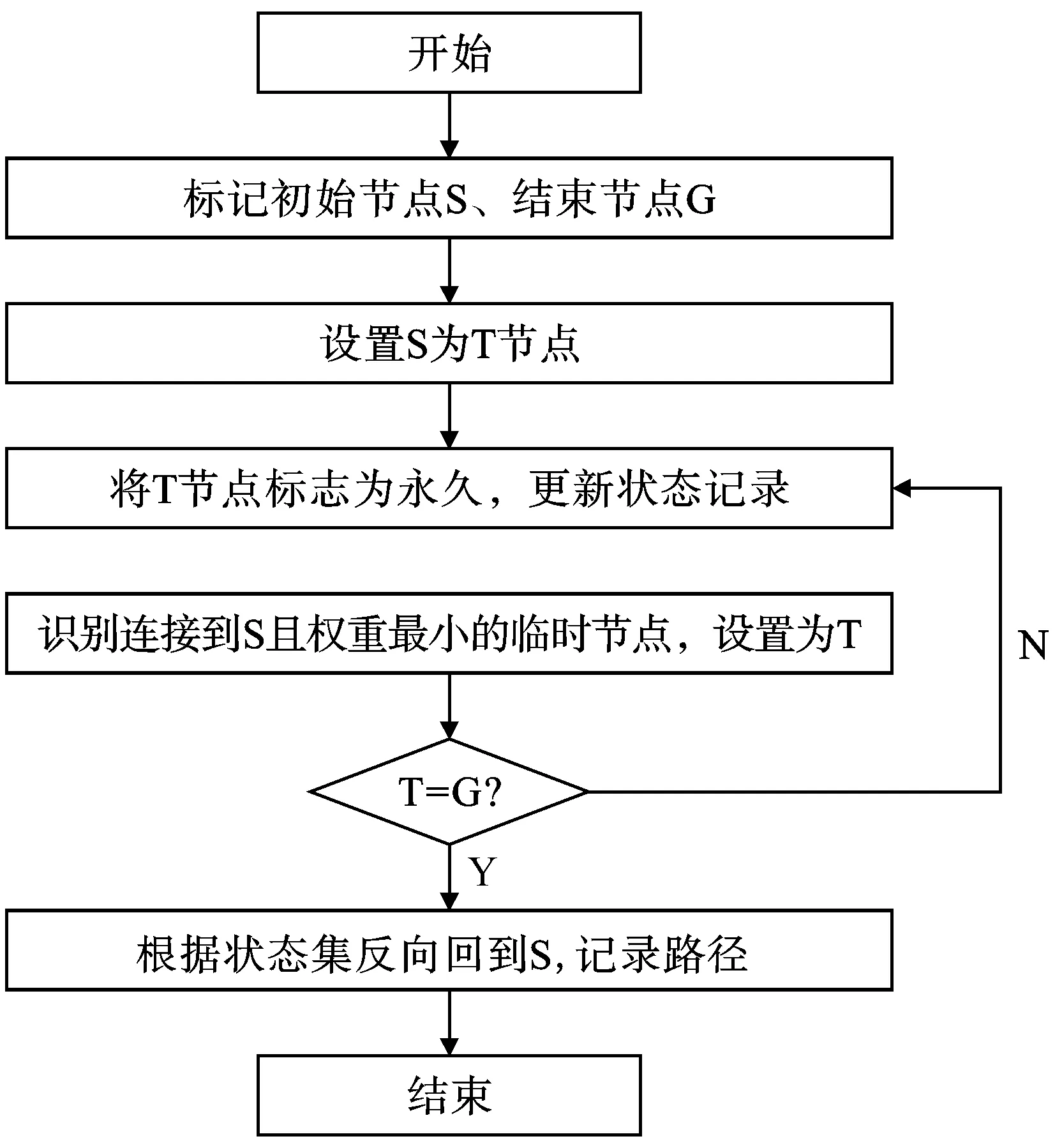
图5 Dijkstra算法简要流程图
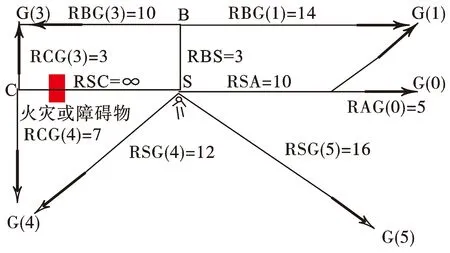
图6 Dijkstra算法简单示例
2.2.2 火灾排斥力Fij
根据火灾的发展和蔓延情况确定最危险区域的元胞格点(行人与疏散动力学的元胞自动机模型通常是二维的,选取正方形格点对区域进行网格划分),距离最危险元胞越近,火灾排斥力数值越大。根据元胞到火灾的距离确定每个火灾元胞对周围元胞的火灾排斥力大小[12],距火灾元胞的距离越小,火灾排斥力越大,距火灾元胞的距离越大,火灾排斥力越小,距离大于一定值时火灾排斥力为0,具体计算如式(3)所示:
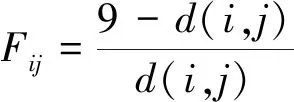
(3)
式中,d(i,j)表示元胞(i,j)到火灾边缘的距离,其相关取值示意图见图7(橙红色方块表示火灾)。在此设置火灾元胞的最大影响半径为8。
假设火灾以着火源为中心向四周以V(火灾元胞的蔓延根据火灾报警器间隔报警的时序进行计算)速度扩散蔓延,根据疏散通道人员密度信息确定
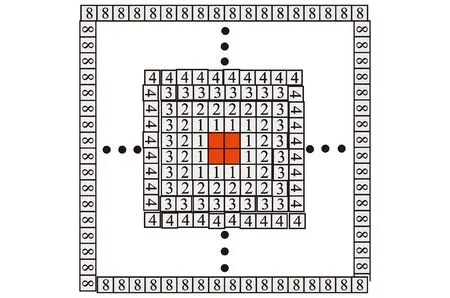
图7 火灾元胞对邻近元胞的影响
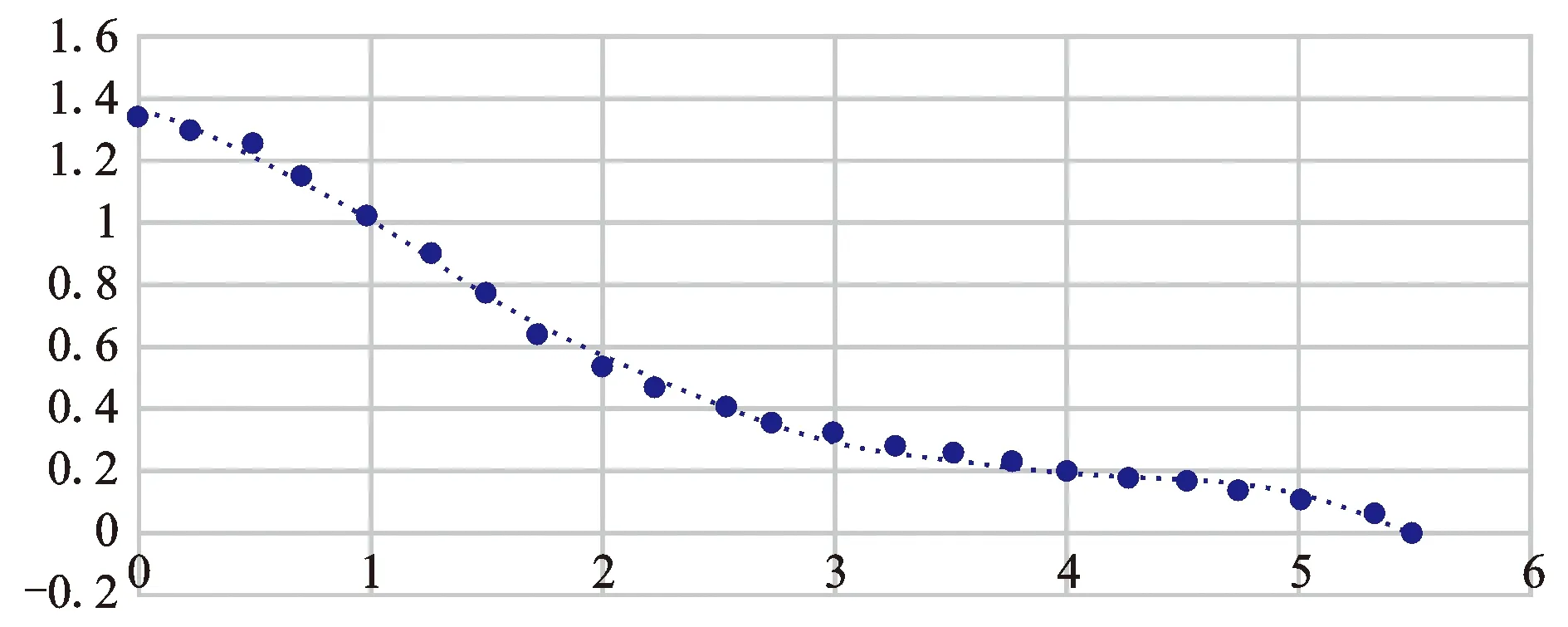
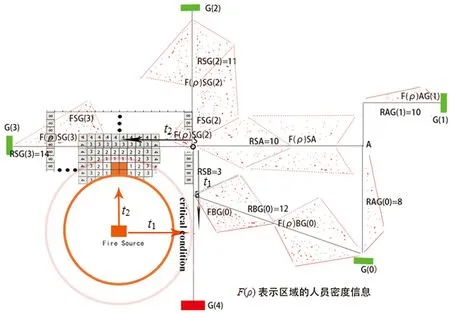
此通道人员的平均速度v。建立方程,确定火灾蔓延是否会影响人员疏散,人员移动下一个时间步概率要充分考虑人员移动到着火点附近Fij的影响。需要考虑的情况如图8所示,s为经过t时刻火灾蔓延的距离,t为人员的疏散时间,当s 图8 火灾蔓延对疏散的影响 2.2.3 人员密度信息Fρij Fρij为元胞j方向疏散通道的人员密度信息(ρij)对当前元胞的影响,决定人员疏散的速度,进而影响人员从当前位置到安全出口的时间。疏散时,并不是利用越近的疏散通道疏散所需的时间越短,在现实生活中,由于人员的盲目性和从众心理,大量人员同时拥挤到同一疏散通道,造成人员密度过大,疏散困难,极易引发踩踏事故。图9为Weidmann水平平面行人运动的经验v-ρ关系[13]。 图9 Weidmann水平平面行人 运动v-ρ经验关系 根据v-ρ经验关系图,经拟合可分析出v-ρ函数关系: 结合火场疏散实际情况,当ρ<0.7 人·m-2时,取v=1.4 m·s-1。 人员在疏散路径上大多数不是均匀分布的,在疏散过程中存在若干连续高密度区间和连续低密度区间,对人员疏散造成影响。距人员越近的连续高密度区间对人员疏散产生的阻力越大,距人员越近的连续低密度区间越有利于人员进行疏散。为区分疏散通道上不同距离高密度区间和低密度区间对人员疏散的影响,式(5)根据密度值将一条疏散路径分为i小段,Li为第i段的长度,ρi为第i段的平均密度信息(可根据视频识别技术提取疏散通道上摄像头的画面来获取),本文加入调节因子k1,k2,k3等,对疏散路径人员密度进行综合评判。 Fρij=[k1ρ1L1+k2ρ2L2+k3ρ3L3+…]/∑iLi (5) 基于对上述影响因素的分析,本文设计出基于Dijkstra算法的智慧疏导系统算法模型如图10所示。 图10 基于Dijkstra算法的智慧疏导模型 图10中G(1)~G(3)代表可以用于疏散的安全出口,G(4)代表因为火灾蔓延而不能选择进行疏散的出口,红色小点代表室内人员,其中火灾蔓延对疏散造成的影响详见图8。当发生紧急情况需要疏散时,算法模型需要综合考虑Sij,Fij,Fρij,l这4个因素的影响,挑选出一条符合用户的实时最佳疏散路径。模型将节点间路径权值R更新设置为综合影响因素φ(Sij,Fij,Fρij,l)(为1/Pij),通过Dijkstra最短路径算法,寻找从起点至终点的最短路径权值的集合,即φ(Sij,Fij,Fρij,l)最小值集合,通过对各路径最小值集合的迭代,找出总体的最小值,即为φ(Sij,Fij,Fρij,l)最小值,Pij的最大值,即所对应疏散方向的最大概率,也即为最优疏散方向。时间步设置为1 s,系统每过2 s或者距节点(A,B,C等)2 m处自动发送请求,重新规划路径。 通过对本模型的分析,确定更新规则为:(1)系统对所有人员进行编号,确保每个人员有独一无二的Id号。(2)确定运动人员,通过室内定位获取用户的具体位置、火灾信息及区域人员信息。(3)确定最佳疏散路径,根据自身坐标判断属于哪个预设子空间,确定此预设空间的出口位置(多个);根据现场路况建立人员密度预测模型,根据获取的当前信息预测当人员疏散至某疏散通道,此通道的人员密度,根据火灾位置信息,建立火灾蔓延模型,计算蔓延对疏散通道上元胞的影响;通过本文提出的基于Dijkstra算法的疏散模型选择当前最佳疏散路径,并保持更新。 智慧化疏散系统已成为未来发展趋势。智慧化不仅仅是单个产品之间实现简单的联动关系,更重要的是如自动处理信号、后台数据融合及计算、生成判定指令、动态调整前端显示等。本文通过了解传统智能疏散系统的优点,同时分析了现有系统存在的缺陷与弊端,引入基于室内定位的智慧疏导系统,较好地解决了现有智能疏导系统存在的问题,并根据基于Dijkstra算法的疏散模型求得疏散的最佳方向,可及时进行更新,以保证现场信息的实时性。本文实现了框架的构建和智慧疏导模型的确定,在今后的研究中,笔者将建立疏散时间预测模型来预测用户选择不同通道进行疏散的预计时间(如百度地图预测到达目的地时间功能);基于误差反向传播原则构建自更新模型对系统中存在的误差进行更新,使系统的判断越来越准确;基于卷积神经网络(CNN)搭建人员密度识别模型,通过分析疏散通道的监控来获取通道上实时人员密度;根据本文建立的框架完成智慧疏导系统的开发,当发生火灾或紧急情况时,软件可结合用户的位置、疏散通道的人员密度、火灾的蔓延发展等因素向用户推荐一条最佳疏散路径,并通过手机客户端显示协助用户进行疏散。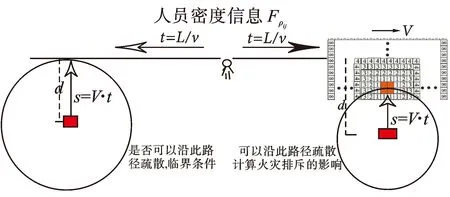
2.3 基于Dijkstra算法确定的智慧疏导模型
2.4 更新规则
3 结语

