大跨径混凝土斜拉桥施工稳定性分析

李海洋，查国鹏，李猛，王佐才

（1.合肥工业大学土木与水利工程学院，安徽 合肥 230009）（2.济南城建集团有限公司，山东 济南 250031）

0 前言

近年来，国内外出现的桥梁事故中，有相当一部分是发生在施工过程中，且大多表现为由局部失稳引起的整体失稳，而稳定性问题在斜拉桥中更为突出。大跨径混凝土斜拉桥一般采用悬浇法施工，在施工时，结构体系一直处于动态变化中，结构的稳定状态也在不断演变，这增加了结构失稳破坏的几率。结构整体失稳时，其势能瞬间释放，带来的结构破坏是灾难性的。因此，国内外有关学者针对斜拉桥施工阶段结构稳定性理论和工程应用问题开展了一系列的研究工作。

卫军、朱玉等[1]（2003）基于第一类稳定分析理论对澳凼三桥（主跨为180m的预应力混凝土双塔斜拉桥）进行了稳定分析。为了研究桥梁运营阶段和最大悬臂施工阶段结构的整体稳定性，采用3D梁单元建立有限元模型，为了研究结构的局部稳定性，采用实体单元建立了局部模型。沈东强、崔国宏等[2]（2006）以北盘江大桥（主跨为495的预应力混凝土双塔斜拉桥）为工程背景，采用MIDAS建立预应力混凝土双塔斜拉桥施工阶段结构模型，基于弹性稳定理论，分析研究双塔斜拉桥独塔施工阶段、最大悬臂施工阶段结构的稳定性，获得了预应力混凝土双塔双索面斜拉桥在施工过程中结构稳定性变化的规律。

罗涛[3]（2009）以营口辽河公路大桥（主跨370m的预应力混凝土双塔斜拉桥）为工程背景，基于非线性有限元理论，采用ANSYS计算程序建立了预应力混凝土双塔斜拉桥有限元模型，然后基于弹性稳定理论，研究了成桥阶段、最大双悬臂和最大单悬臂施工阶段结构在半漂浮和全漂浮两种不同体系下的稳定性，获得了相应的结构前5阶特征值和特征向量，即结构稳定安全系数和失稳模态，明确了边界条件以及配重对施工阶段结构稳定性的影响规律。

西南交通大学陈文元老师[4]（2011）以鄂东长江大桥（双塔混合梁斜拉桥）为工程背景，基于特征值屈曲理论，分别采用两种仿真计算软件独立进行仿真计算，经过对比分析，得到了该桥施工全过程的弹性稳定安全系数，明确了各施工阶段结构弹性失稳模态，获得了钢箱梁斜拉桥施工阶段结构稳定性变化规律。

Yang-Cheng Wang[5]（1999）以Agrawal论文中三个斜拉桥例子为研究背景，采用数值分析方法检验这些斜拉桥例子的二维有限元模型，通过特征值分析获得了斜拉桥最小临界屈曲荷载，并着重研究了斜拉索数量与桥梁整体屈曲荷载之间的关系。研究结果表明，随着斜拉索数量的增加，单根斜拉索索力减小、斜拉索最大索力值减小，但是主梁承受的轴力增大，此时，结构的失稳控制构件由斜拉索转变为主梁桥面板，由桥面板承受的轴向压力来控制临界屈曲荷载，因此增加斜拉索的数量不一定能导致结构临界屈曲荷载的提高。斜拉桥基本屈曲临界荷载与桥面板惯性矩和桥塔惯性矩的比值正相关，直到比值达到最优值；当比值超过了最优值时，斜拉桥屈曲临界荷载开始下降，同时，斜拉桥基本屈曲临界荷载不仅仅由桥面板惯性矩和桥塔惯性矩的比值决定，还与斜拉桥的类型一级斜拉索的数量有关。

Hoon Yoo、Ho-Sung Na和Dong-Ho Choi[6]（2011）提出一种简单的估算大跨径钢斜拉桥极限破坏荷载的新方法，为考虑梁柱效应的斜拉桥整体特征值迭代计算提出一种新的收敛判别准则。采用该方法和收敛判别准则对中型和大跨径两个斜拉桥例子进行了极限破坏荷载的估算，并与传统的非线性弹塑性理论计算的极限破坏荷载和破坏形式进行了比较，结果表明新方法可行。

1 结构稳定有限元理论

结构的稳定性是结构重要的安全指标，指结构在外荷载作用下，能够继续保持结构初始平衡状态的能力。稳定问题是力学问题中的一个重要的分支，是桥梁工程中常需解决的问题，有着十分重要的意义，通常可分为第一类稳定问题和第二类稳定问题。第一类求解过程简单，如著名的欧拉临界荷载问题，第二类稳定过程求解繁杂，需要进行全过程受力分析，但是其结果对工程实践更具有指导意义。

1.1 第一类稳定性问题

根据有限元和弹性力学稳定性理论，结构平衡方程的增量形式可表示为

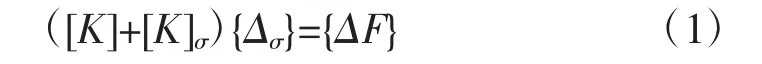
式（1）中[K]为弹性刚度矩阵，[K]σ为几何刚度矩阵，{△σ}为节点位移增量矩阵，{△F}为节点荷载增量矩阵。

结构达到临界状态时，{△F}→0，方程（1）有非零解，则

当结构处于小变形的状态时，[K]σ与结构的应力水平成正比，因而结构在临界荷载下几何刚度矩阵可以表示为

将式（3）代入式（2）中可以得到

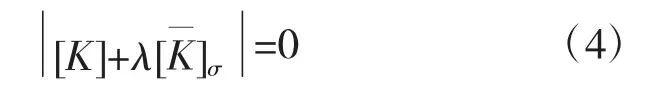
式（4）就是推导出的第一类稳定问题的控制方程。通过求解此控制方程，可获得矩阵的特征值与特征向量，它们分别对应结构的安全系数和失稳模态。

1.2 第二类稳定性问题

第二类稳定问题的实质是结构的极限承载力评估，它更接近于实际工程中常出现的失稳破坏，更具有参考价值。

计入几何非线性影响的结构平衡方程的增量形式

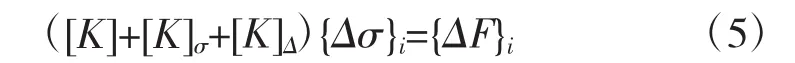
式（5）中[K]△为大位移刚度矩阵,{△σ}i为第 i次加载{△F}i时产生的节点位移增量。

第二类稳定问题常采用全过程分析方法，在分析时需要考虑结构的各种非线性影响，其主要求解思路是：通过逐级增加荷载，不断观察结构的受力变形特点，当结构出现规范规定的承载能力极限状态表现特征时，认定结构达到其极限承载力而破坏，此时结构的外荷载不再增加，但结构变形将急剧增加。

2 工程概况及有限元模型的建立

2.1 工程概况

宣城市水阳江特大桥是三跨双塔双索面半漂浮体系斜拉桥，桥梁全长620m,采用150+320+150m的跨径布置方式，其跨径布置如图1所示。

图1 水阳特特大桥跨径布置图（单位:cm）

2.2 有限元模型的建立

依据现场收集的监控资料结合设计图纸，建立水阳江特大桥有限元模型。整个计算模型划分为763个节点和572个单元，包括176个索单元和396个梁单元。斜拉索与主梁和塔柱之间锚固采用弹性连接模拟。水阳江特大桥有限元计算模型如图2所示。

图2 水阳特特大桥有限元计算模型

3 施工全过程稳定性分析

为确保每个施工阶段结构的稳定性满足规范要求，按照实际施工流程，对水阳江特大桥进行分阶段弹性稳定性分析，得到各施工阶段的弹性稳定安全系数并与规范对比分析判断出当前阶段结构是否安全。

在Midas/Civil通用仿真环境下，分别建立每一施工阶段结构的独立有限元模型，并以当前施工阶段结构块段的自重作为施工荷载基数计算结构稳定安全系数。通过Midas/Civil特征值屈曲分析模块，计算得到了结构整体失稳时的屈曲特征值、特征向量以及各个施工阶段结构的整体线弹性稳定安全系数和相应的失稳模态。计算得到的水阳江特大桥施工全过程弹性稳定安全系数变化情况如图3所示。

图3 水阳江特大桥施工全过程弹性稳定安全系数

从图3分析可知，水阳江特大桥施工过程中弹性稳定安全系数最小为12.75发生在中跨合龙施工阶段后，满足《公路斜拉桥设计细则》关于弹性稳定安全系数不小于4的要求。

由最大双悬臂状态到边跨合龙阶段，弹性稳定安全系数由21.49增大至40.43，是由于边跨合龙增强了结构体系刚度,因而增强了结构的稳定性。由最大单悬臂状态到中跨合龙施工阶段，弹性稳定安全系数由17.8降低至14.58，是由于在该阶段，结构体系转换，拆除了塔梁的临时固结和边跨临时支承，边界条件的减弱导致斜拉桥整体刚度有所降低，从而降低了结构的稳定性。

水阳江特大桥在施工过程中，结构失稳模态主要表现为主塔面外失稳和主梁面内竖弯。水阳江特大桥施工过程中最大单悬臂施工阶段失稳模态如图4所示。

图4 水阳江特大桥施工过程（最大单悬臂）失稳模态

4 设计参数对施工过程稳定性影响分析

由于实际施工过程中会出现部分不可控因素，这将会导致结构的实际参数与设计理论参数存在差异，并影响结构的稳定性，因此需要进行参数分析，厘清这些设计参数与结构稳定性之间的具体关系。论文选取混凝土容重、塔梁的刚度和施工临时荷载等相关设计参数对施工过程稳定性影响分析。

4.1 混凝土容重对稳定性影响分析

对于水阳江特大桥主梁和主塔采用混凝土材料，在施工过程中存在混凝土浇筑超方的现象，通过实际施工时混凝土容重与设计误差控制在5%范围以内，分别增大3%、5%，论文通过将主梁和桥塔的混凝土容重分别增加3%、5%，分析混凝土容重引起的误差对水阳江特大桥稳定性分析，在三种工况下计算得到施工过程稳定安全系数如图5所示。

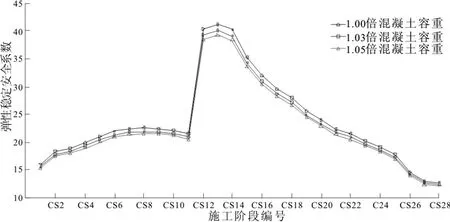
图5 混凝土容重对施工过程稳定性影响分析

由图5分析可知，混凝土容重增大导致各个施工阶段弹性稳定性系数有所下降，但是并不明显。施工过程中弹性稳定系数最小值发生在中跨合龙施工阶段以后，分别为14.58、12.96和12.75。

在最大双悬臂施工阶段，混凝土容重增加3%和5%导致该施工阶段稳定安全系数减少了3.2%和4.7%。在最大单悬臂施工阶段，混凝土容重增加3%和5%导致该施工阶段稳定安全系数减少3.5%和5.5%。

4.2 结构刚度对稳定性影响分析

斜拉索通常在工厂进行预制，其截面尺寸及弹性模量均能够得到保证，因而对结构刚度的影响可以不用考虑。对于水阳江特大桥，塔梁均采用混凝土现场浇筑施工，存在截面尺寸误差及弹性模量等与设计值有差异。根据单一变量的原则，选取弹性模量作为塔梁刚度控制变量进行施工过程稳定性影响分析，论文选取塔梁弹模的0.9倍和1.1倍进行施工过程稳定系数分析。其中主梁和对施工过程稳定性影响如图6所示。

由图6分析可知，主梁刚度在设计值的10%范围内变化，对各施工阶段稳定安全系数影响很小，且施工过程弹性稳定系数满足规范要求。

经过有限元模型计算得到桥塔刚度对施工过程稳定性如图7所示。

由图7分析可知，桥塔刚度在设计值的10%范围内变化，对施工过程稳定安全系数产生一定的影响，最大影响值可达11%，中跨合龙后桥塔刚度变化对弹性稳定系数基本没有影响。

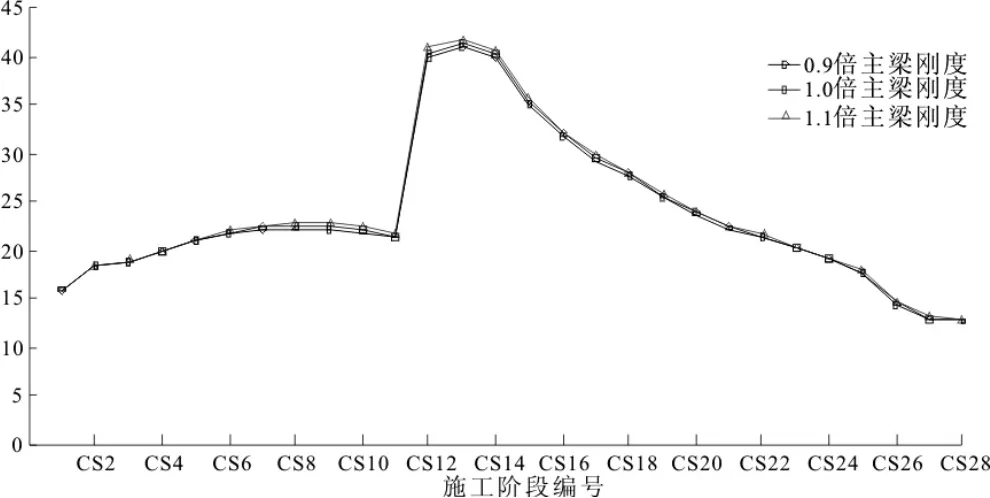
图6 主梁刚度对施工过程稳定性影响分析

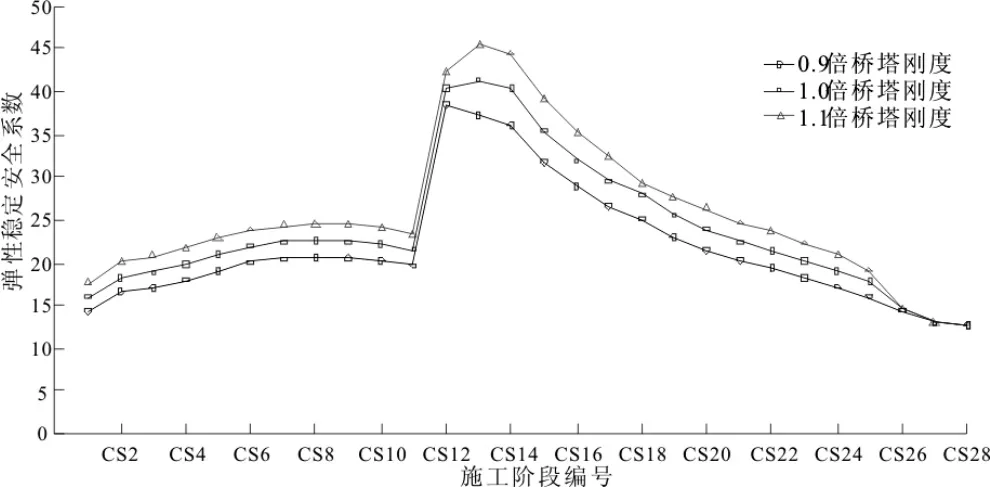
图7 桥塔刚度对施工过程稳定性影响分析

由图6和图7可知，桥塔的刚度变化对施工过程稳定性影响程度要高于主梁，施工过程中的各种失稳模态基本表现为桥塔的失稳。因此，在施工过程中要严格控制桥塔的弹性模量和截面尺寸，保证施工过程中结构稳定性满足要求。

4.3 施工临时荷载对稳定性影响分析

水阳江特大桥施工临时荷载主要有挂篮和其他施工临时荷载，设计中施工临时荷载总重量取值为2500kN，在实际施工过程施工临时荷载与设计中施工临时荷载有一定的区别。论文中按设计施工临时荷载总重量的0.8和1.2倍来考虑施工临时荷载对施工过程稳定性的影响，共选取0.8倍、1.0倍和1.2倍3个计算工况进行对比分析，三个计算工况如表1所示。

表1 施工临时荷载计算工况

通过有限元软件计算得到不同施工荷载工况对施工过程稳定性影响分析如图8所示。

由图8分析可知，施工临时荷载在设计值的0.8～1.2倍范围内，其改变值对施工阶段稳定性几乎没有影响，可以忽略不计。施工过程中施工临时荷载重量在设计值的0.8～1.2倍范围内对称布置施工机械不影响施工过程中稳定性。

图8 施工临时荷载对施工过程稳定性影响分析

5 结论

本文对水阳江特大桥进行了施工阶段全过程稳定性分析，研究了结构设计参数对施工过程稳定性的影响，主要内容与结论如下:

①对水阳江特大桥进行施工全过程稳定性分析，结果表明，整个施工过程中结构的弹性稳定安全系数均满足规范要求。从失稳模态上来看，边跨合龙前均以桥塔的平面内失稳为主，边跨合龙后以桥塔的平面外失稳为主。

②对混凝土容重、塔梁弹模和施工临时荷载等结构设计参数对施工过程稳定性进行分析，混凝土容重为设计值的1.03～1.05倍、主梁刚度为设计值的0.9～1.1倍和施工临时荷载在设计值的0.8～1.2倍范围内变化对施工过程稳定性影响较小。

③桥塔刚度变化在10%范围内，对施工过程稳定性影响较大，对施工过程稳定系数影响值最大可达11%，在施工过程中需要控制桥塔弹模和截面尺寸。