基于流固耦合的管道车振动运移水力特性数值模拟与试验
张春晋, 孙西欢,2, 李永业, 张学琴
(1.太原理工大学 水利科学与工程学院,太原 030024;2.晋中学院,山西 晋中 030600;3.章丘黄河河务局,济南 250200)
筒装料管道水力输送(是一种新型节能环保的运输方式,具有成本低、占地少、效率高和绿色环保等优势,适合运输工业材料、化工原料和农产品等固体物料。该技术原理是将物料密封在管道车内部,并借助流体的推力在管道内进行物料的长距离运输。
目前,许多国内外学者已经对筒装料管道水力输送展开了大量的研究。孙西欢等[1-3]分析了管道车临界启动状态下管道车荷载与起动流速之间的关系,并探讨了不同型号的管道车在管道内运移的水力特性。Khalil等[4-5]研究了在不同雷诺数条件下管道车运移时的水力特性,并结合管道车的动力学机理,将管道车的运移过程划分为悬浮,振荡和稳定等3个典型阶段。Mishra等[6-8]采用模型试验研究了在弯曲和倾斜管道内管道车运移时的水动力学特性,并建立了管道车速度与局部能耗之间的半经验公式。Wang等[9-10]研究了动边界条件下管道车平均运移速度与环状缝隙流流动特性之间的关系,并推导出了筒装料管道水力输送的最佳输送雷诺数。Sub等[11-13]结合紊流的基本关系和Von Karman相似性假设,分析了不同管道车直径比对动边界同心环状缝隙流的流速与动水压强的影响效应。Polderman等[14-15]研究了管道车运动时环状缝隙内部润滑流体、牛顿流体和非牛顿流体的水力特性,并将试验结果与三层梯度扩散模型进行了对比分析。张琪琦等[16-18]对管道车运移时的摩擦阻力、进流收缩和出流扩张等3种能耗损失进行了理论分析,并采用模型试验研究了不同环隙比条件下管道车单位水头损失与环状缝隙流轴向流速之间的分布规律。郭晓朦等[19-20]研究了不同输送荷载的管道车在平直管道运移时的管道车上游流场的三维流速分布与脉动强度。上述研究成果主要采用模型试验的方法进行分析,受到试验仪器和流场复杂性的诸多限制,目前无法全面获得管道车运移过程中管道内部流场复杂的水力特性。
随着电子计算机的飞速发展以及商业CFD(Computational Fluid Dynamics)软件的日臻成熟,近年来流固耦合数值模拟逐渐成为了分析流体机械水力特性的重要研究方法。流固耦合数值模拟考虑到了流体与结构之间的耦合作用,涉及到流体域和固体域的双重求解,计算结果将更加接近物理现象本身的变化规律。目前,流固耦合数值模拟在离心泵和水轮机等旋转机械方面[21]取得了一定的研究成果,但是对于筒装料管道水力输送流固耦合的研究还鲜有涉及。
筒装料管道水力输送技术中管道内部流场与管道车之间存在明显的流固耦合作用。一方面,管道车在流体载荷的作用下产生动力学响应;另一方面,管道车动力学响应反过来影响管道流场的水力特性,改变流体载荷的分布和大小。如果将管道车视为匀速运动,则忽略了管道流场水力特性对于管道车动力学响应的影响,这与试验结果存在较大误差。为此,对于管道车与管道流体之间进行流固耦合求解十分必要。
本文的研究目的是以车长为100 mm和直径为60 mm的管道车作为主要研究对象,运用ANSYS Fluent 12.0对管道车结构响应和管道内部流场进行流固耦合数值模拟,从而进一步分析管道车在平直管段振动运移的水力特性。本文的研究不仅弥补了试验研究中存在的不足,而且提高了管道内部流场水力特性与管道车瞬态结构响应的计算精度。
1 材料与方法
1.1 管道车设计
管道车结构包括料筒、支撑体和万向滚珠,如图1所示。料筒为空心的有机玻璃圆柱体。支撑体是由细圆柱体和薄钢板2部分组成,支撑体呈120°等间距放射状布置在料筒的前后端面,可使管道车在管道内保持同心位置,有效克服管道车运移过程中的不稳定问题。万向滚珠安装于支撑体末端,可减小管道车与管道间的摩擦阻力,起到节能作用。管道车荷载为8 mm直径的钢珠,钢珠间隙通过橡胶海砂填充。

图1 管道车结构
1.2 试验平台
试验平台包括动力装置、控制装置、输送管道和回收装置,如图2所示。动力装置包括试验水箱和离心泵。控制装置包括控制阀、电磁流量计和管道车制动装置。输送管道为有机玻璃管段和钢管段,全长28.62 m,直径100 mm,壁厚5 mm,不同管段间均由法兰密封连接。矩形水槽布置在有机玻璃管段用于防止试验测量时激光在管道内发生折射。回收装置包括管道车投放口、塑料集车箱、稳流板和海绵。试验时,水流由离心泵从试验水箱抽入有机玻璃管段。调节管道流量,待流量稳定后,将管道车从投放口注入输送管道内。当管道车运移到试验测试段面时,对管道内相应测点的流速与压强进行测量。试验结束后,管道车通过塑料集车箱离开输流管道。与此同时流体再次流回试验水箱,整个过程形成了闭合的循环回路。

图2 试验平台(m)
1.3 试验方案和试验流程
采用车长100 mm,直径60 mm的管道车进行试验,管道车荷载为600 g,流量为40、45、50、55、60、65及70 m3/h。试验方案中试验测试段为5.8 m,距下游弯管进口断面和上游管道车制动装置分别为2.7和4.7 m。试验测试段布置1#、2#、3#及4#测试断面,距离试验测试段进口断面分别为2.4、2.5、2.6及2.7 m,且4个测试断面的流速测点布置一致。测点位于间距为0.015 m的七等分水平线与间距0.01 m的五等分测环的交叉点,共布置43个流速测点。压强测点沿着试验测试段布置,间隔为0.5 m,共布置11个压强测点。试验时,每个试验测点重复测量3次,并取其平均值。
管道车在平直管段振动运移的水力特性包括管道瞬时断面流速、沿程瞬时测压管水头和管道车瞬时速度。根据试验方案,本文的试验流程为:其中美国TSI公司的多普勒激光流速仪和江苏扬泰光电公司的毫秒光电计时器用来联合测试试验测试段不同断面处管道瞬时流速分布。成都泰斯特电子信息有限责任公司的压力传感器和标准动态压强采集盒测量管道沿程瞬时测压管水头。日本NAC公司的Memrecam GX-3高速摄像机测量管道车的瞬时速度。最后,将所有试验数据都通过Excel 2013传输至计算机,并采用Suffer 11.0、Origin 9.0等软件对数据进行统计分析。
2 流固耦合计算方法
2.1 内部流场数值计算
采用Auto CAD软件建立筒装料管道水力输送的几何模型,如图3所示。几何模型包括管道模型和管道车模型2部分,管道模型5.8 m,该长度与试验测试段长度一致。管道模型包括进口管段、运动管段和出口管段。运动管段为5.2 m,进口管段和出口管段分别为0.3 m。进口管段使管道内紊流充分发展,而出口管段则降低了管道车对几何模型出口断面的影响。

注:AB表示几何模型进口断面,CD表示几何模型出口断面,E表示管道车模型
管道车模型参数:料筒长度为0.1 m,直径为0.06 m;支撑体细圆柱体长度为0.017 m,直径为0.008 m;支撑体薄钢板长度为0.015 m,高度为0.028 m,厚度为0.001 5 m;万向滚珠直径为0.008 m;管道车荷载为600 g。管道模型进口断面圆心为坐标原点,管道车中心的初始位置距管道几何模型进口断面为0.5 m。管道车初始时刻流场计算域和管道车固体域网格加密如图4所示。

(a) 流场计算域网格加密
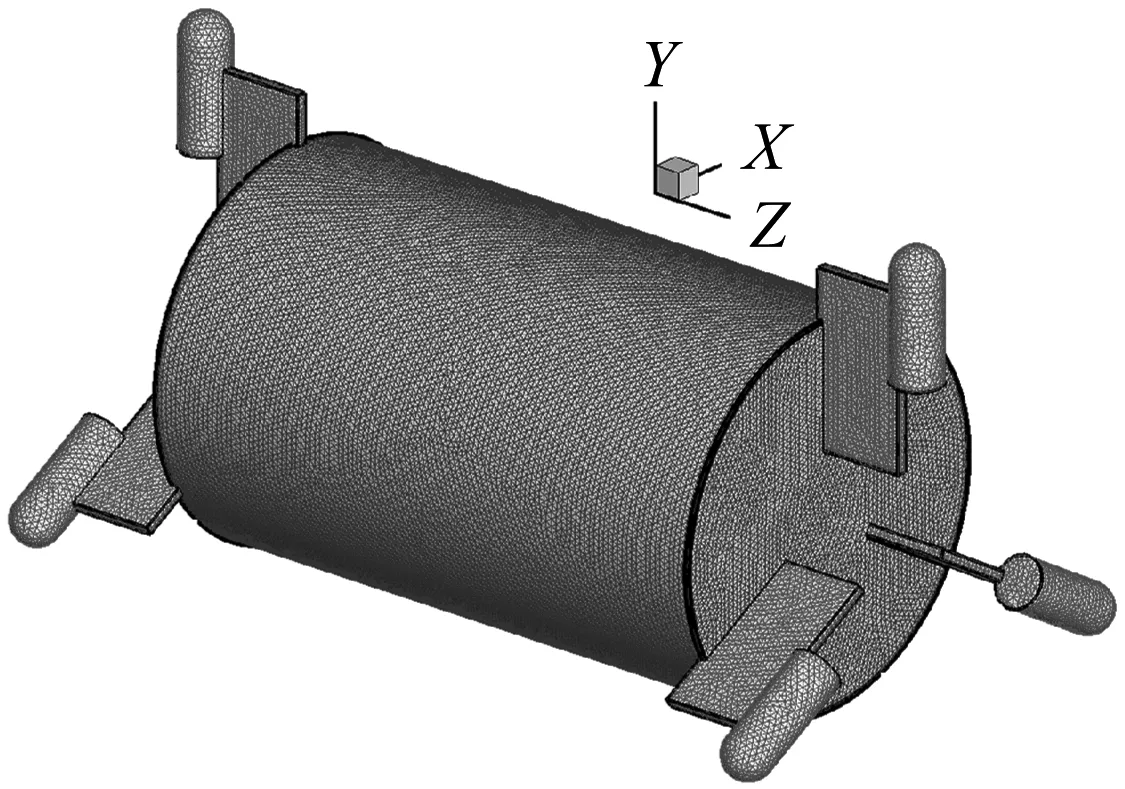
(b) 管道车固体域网格加密
采用ICEM软件对几何模型的计算域进行网格加密,如图5所示。本文的计算域分为流场计算域与管道车固体域2部分。流体计算域运动管段宜采用四面体的非结构化网格进行网格加密,而管道模型进口管段和出口管段均宜采用与四面体网格相同尺寸的六面体的结构化网格进行加密。通过2 mm与3 mm两套体网格对非定常计算进行网格无关性检验[22],两者的几何模型进出口断面压强差的相对误差小于1%,同时将模拟值与试验值进行对比,得出模拟值与试验值基本吻合。因此,本文选择2 mm网格对流场计算域进行数值模拟。为提高管流场的计算精度,还采取了管道近壁面边界层加密和管道车局部面网格加密。通过计算得到的管道近壁面黏性底层厚度约为0.000 6 m,为此第一层网格为0.000 1 m,递变梯度为1.2,共设置5层边界层网格。管道车局部壁面采用0.001 m的三角形非结构化网格进行加密。
采用压力-速度耦合的PISO算法求解不可压缩黏性流体的连续性方程和雷诺时均方程。紊流模型采用RNGk-ε紊流模型,可以精确模拟管道车近壁面流场区域的水力特性。控制方程的对流项均采用二阶迎风格式进行离散[23]。非定常计算时间步长为10-5s,各控制方程收敛残差为10-4。
根据图4,对筒装料管道水力输送的几何模型设置边界条件。进口边界(AB)为流速进口。本文根据试验测试段进口断面实测流速,采用UDFs(User Defined Functions)函数定义进口断面流速分布,其中流体密度为1.0×103m3/h,动力黏度为1.062×10-3Pa·s(水温18 ℃)。出口边界(CD)为压强出口,采用压强实测值定义出口断面的压强分布。紊流强度和紊流耗散率依据经验公式确定。管道边界(AC、BD)为无滑移边界,近壁区域采用标准壁面函数法处理。管道车边界(E)采用6DOF(6 Degree of Freedom)耦合模型和UDFs函数进行定义。UDF函数定义管道车转动惯量、摩擦阻力、运移范围和初始状态。管道车边界仅存在Z方向的移动自由度和Z方向的旋转自由度。管道车初始的瞬时速度采用管道车的实测瞬时速度进行定义。进口管段、运动管段和出口管段之间的对应面均设置为Interface边界条件。
2.2 结构动力学方程
6DoF耦合模型中,管道车结构动力学方程为[24]
Mu″+Cu′+Ku=Fs+FFSI
(1)
式中:M为质量矩阵,kg;C阻尼矩阵,N·s/m;K为刚度矩阵,N/m;u″为节点加速度,m/s2;u′为节点速度m/s;u为节点位移,m;Fs为非流体作用荷载;FFSI为流体作用于管道车的耦合力。为了提高计算的精度,采用Newmark隐式时间积分法对结构动力学方程进行求解。在耦合交界面处,流体与固体的位移和应力等相互耦合变量应相等或守恒。控制方程为[24]
nτf=nτs,rf=rs
(2)
式中:τ为耦合面处应力,Pa;r为耦合面处位移,m;n为法向矢量;下标f为流体;下标s为固体。
6DOF耦合模型是利用结构动力学方程求解管道车的瞬时速度与位移。结构动力学方程中的流体荷载可通过6DOF耦合模型直接求解,而非流体荷载则需通过UDFs函数进行辅助定义。本文中非流体荷载的滚动摩擦阻力是利用管道车与管道间的实测滚动摩擦阻力的摩擦系数与管道车Y方向的瞬时合力值的乘积进行计算。6DOF耦合模型中需考虑管道车的重力。
2.3 流固耦合求解方法
本文应用RNGk-ε紊流模型对管道车在平直管段运移的水力特性进行数值计算。结合6DOF耦合模型和UDFs函数对管道车结构响应进行分析。耦合界面实现流体域数据与固体域数据的实时交换。流固耦合作用引起管道车产生了位移效应,采用弹性光顺和网格重构的动网格技术对计算域网格进行实时修正[25]。
流固耦合分析流程,如图5所示。
(1) 根据固体的结构响应,结合动网格技术对流体域网格进行修正。并以固体的位移和速度作为流体域的初始边界条件进行流场的迭代计算,直至流场结果收敛,从而得到作用在固体结构表面的流体荷载;
(2) 通过耦合界面将该流体载荷施加到固体结构。采用6DOF耦合模型计算管道车的瞬时位移和速度;
(3) 当管道车位移在运移范围内时,将管道车速度和位移作为下一时刻流体域的边界条件继续求解。如此反复,直至管道车运移到计算域指定边界为止。

注:Sc为管道车中心到几何模型进口断面处的距离,S为管道车的运移范围
3 计算结果与分析
3.1 管道车运移速度模拟与验证
图6为管道车瞬时速度模拟值与试验值对照图。

(a) Q=50 m3/h, Vb=1.132 4 m/s

(b) Q=60 m3/h, Vb=1.571 1 m/s
从图6可知:
(1) 模拟值与试验值一致,相对误差不超过4.6%。
(2) 管道车运移过程中瞬时速度在一定范围内呈振动变化,因此,可以将管道车在平直管段的振动运移视为恒定运动。
(3) 管道车瞬时速度呈无规则振动变化。原因是流体脉动压强的无规则波动将引起管道流体对管道车的瞬时荷载产生波动性变化,进而引起管道车的瞬时加速度发生变化,使得管道车在管道内振动运移。
3.2 模型流速场模拟与验证
图7为管道车中心运移到距几何模型进口断面2.5 m位置时,不同断面水平极轴处轴向流速模拟值与试验值对照图。
从图7可知:
(1) 模拟值和试验值一致,相对误差不超过4.8%。
(2) 管道车上游流场断面轴向流速呈指数型分布趋势。原因是管道内流体仅向下游传播,因此管道车上游流场的轴向流速将呈现出指数分布的变化规律。
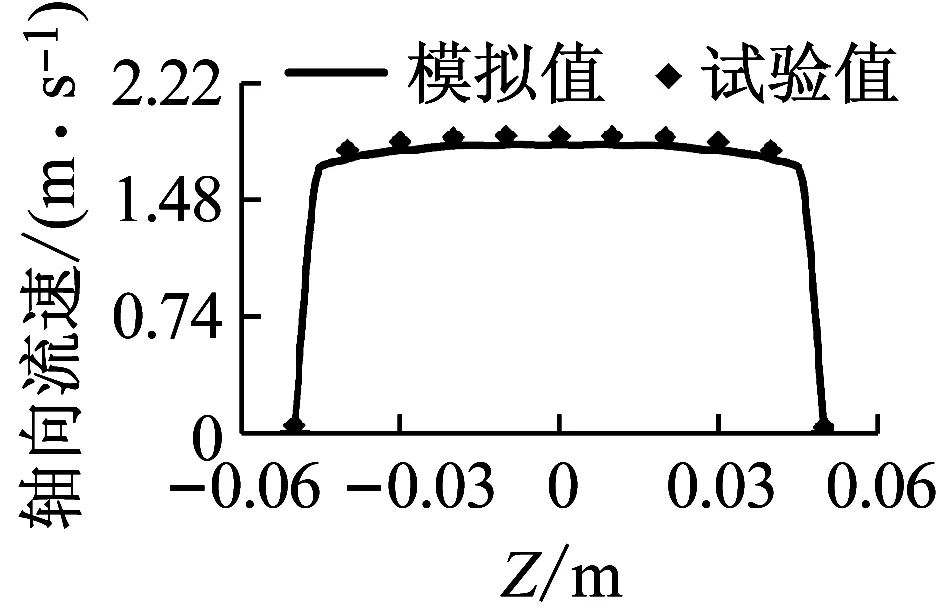
(a)Q=50 m3/h,1#断面区域

(b)Q=50 m3/h,2#断面区域

(c)Q=50 m3/h,3#断面区域

(d)Q=50 m3/h,4#断面区域

(e)Q=60 m3/h,1#断面区域

(f)Q=60 m3/h,2#断面区域

(g)Q=60 m3/h,3#断面区域

(h)Q=60 m3/h,4#断面区域
(3) 管道车下游流场断面轴向流速呈中间低,两边高的变化趋势。原因是管道车环状缝隙流与其下游管道流体产生相互作用,使得环状缝隙流向管道车下游流场扩散过程中引起了局部回流现象,因此管道车下游的近壁面中央区域将出现低流速区。
图8为Q=50 m3/h流量条件下,不同时刻管道车运移时水平断面轴向流速分布云图。
从图8可知:
(1) 管道车下游流场区域存在明显的低流速区。原因是环状缝隙流向管道下游流体过渡过程中在管道车料筒的近壁面发生了边界层分离现象,主流离开料筒曲面,而下游流体随即回填空腔区域。
(2) 管道车运移过程中环状缝隙区域出现了两处高流速区。第1处出现在环状缝隙流进口区域,由于环状缝隙进口区域产生的边界层分离现象所导致的;第2处出现在环状缝隙流的出口位置,由于管道车下游流体回流补充环状缝隙出口区域的流体所引起的。

(a) t=0.5 s,Sc=1.072 m,Vc=1.138 2 m/s

(b) t=1.0 s,Sc=1.638 m,Vc=1.122 5 m/s

(c) t=1.5 s,Sc=2.191 m,Vc=1.141 4 m/s

(d) t=2.0 s,Sc=2.769 m,Vc=1.132 7 m/s

(e) t=2.5 s,Sc=3.337 m,Vc=1.143 8 m/s
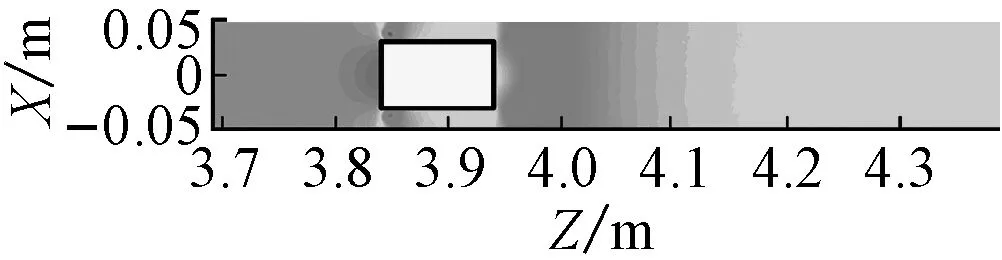
(f) t=3.0 s,Sc=3.891 m,Vc=1.125 6 m/s

(g) t=3.5 s,Sc=4.458 m,Vc=1.135 1 m/s

(h) t=4.0 s,Sc=5.031 m,Vc=1.129 3 m/s
(3) 管道车上游流场受到管道车的干扰较小。原因是管道内流体为急流,仅向管道车下游方向传播。
(4) 管道车运移时不同时刻的管道水平断面轴向流速分布基本一致。原因是管道车稳定运移过程中瞬时速度的变化幅度较小,使得管道车与管道流体之间组成的耦合系统的瞬态运动要素处于恒定状态。
3.3 模型压强场模拟与验证
图9为管道车运移到不同位置时,管道沿程测压管水头模拟值与试验值对照图。
从图9可知:
(1) 模拟值和试验值一致,相对误差不超过4.2%。
(2) 管道车运移位置的近壁面流场区域呈现出了“W”型的测压管水头分布规律。原因是管道流体受到管道车车后端面处支撑体的作用,引起管道断面突然束窄,流体流速升高,导致管道压强降低。随后流体进入环状缝隙区域,管道系统的流速降低,引起缝隙区域的压强逐渐回升。在管道车下游区域,环状缝隙流与管道车下游近壁面流体发生相互作用,使得管道车下游近壁面区域流场产生了巨大的旋涡损失,因此管道车下游近壁面区域压强急剧降低。与此同时,环状缝隙流体在扩散过程中将动能转化为下游流体的压能,使得流体压强又再次回升。因此,在管道车近壁面流场区域形成了“W”型的测压管水头变化趋势。

(a) Q=50 m3/h,Sc=1.5 m

(b) Q=50 m3/h,Sc=2.5 m

(c) Q=50 m3/h,Sc=3.5 m

(d) Q=50 m3/h,Sc=4.5 m

(e) Q=60 m3/h,Sc=1.5 m

(f) Q=60 m3/h,Sc=2.5 m

(g) Q=60 m3/h,Sc=3.5 m
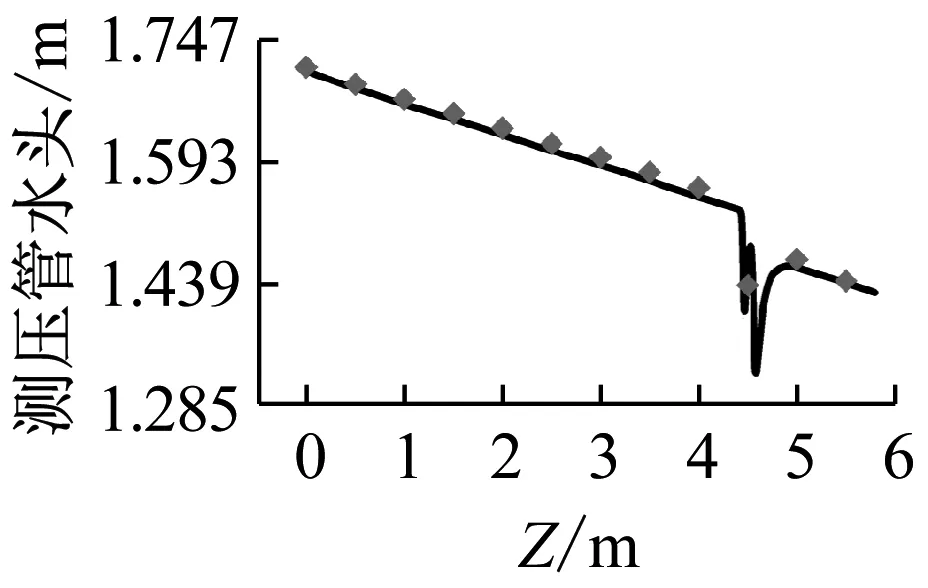
(h) Q=60 m3/h,Sc=4.5 m
(3) 管道车上、下游流场压强呈逐渐降低的线性变化趋势。原因是根据达西公式可知沿程压强损失与管道长度呈线性负相关。
图10为为Q=50 m3/h流量条件下,不同时刻管道车运移时水平断面压强分布云图。
从图10可知:
(1) 管道车上游近壁面区域出现了局部高压区。原因是管道车上游流体在管道车的作用下,流体将动能转化为了局部压能。
(2) 管道车下游近壁面流场区域出现了低压区。原因是管道车环状缝隙流体与管道车下游流体产生相互作用,环状缝隙流的动能逐渐转化为管道车下游流体的压能,并且环状缝隙流的边界层分离引起管道车下游产生了旋涡损失。在两者共同作用下,使得管道车下游近壁面流场区域的压强将急剧降低。

(a) t=0.5 s,Sc=1.072 m,Vc=1.138 2 m/s
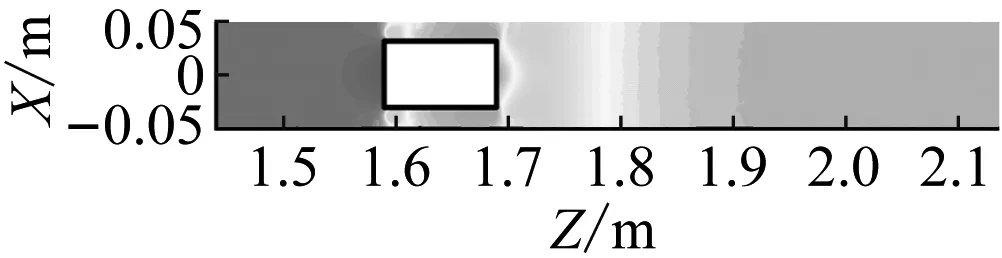
(b) t=1.0 s,Sc=1.638 m,Vc=1.122 5 m/s

(c) t=1.5 s,Sc=2.191 m,Vc=1.141 4 m/s

(d) t=2.0 s,Sc=2.769 m,Vc=1.132 7 m/s
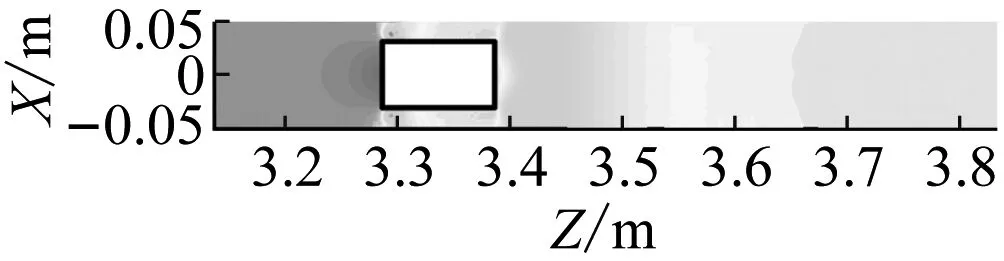
(e) t=2.5 s,Sc=3.337 m,Vc=1.143 8 m/s

(f) t=3.0 s,Sc=3.891 m,Vc=1.125 6 m/s

(g) t=3.5 s,Sc=4.458 m,Vc=1.135 1 m/s

(h) t=4.0 s,Sc=5.031 m,Vc=1.129 3 m/s
(3) 管道车车前端面出现了“半圆形”的高压区。原因是环状缝隙流向上游回流过程中受到管道车的阻碍作用,使得回流流体将动能部分转化为了压能。
4)随着管道车运移时间的增长,管道车局部压强分布呈现整体降低的变化趋势。原因是管道车局部压强与管道沿程压强变化趋势一致。由于管道内部压强沿程逐渐降低,所以管道车的运移位置越靠近下游区域,则管道车局部压强将表现出降低的变化趋势。
3.4 管道车能耗分析
图11为管道车运移时平均能耗随管道流量的变化规律。管道能耗是指管道车运移的局部能耗与管道流体引起的管道沿程能耗损失之和。管道车与流体之间的流固耦合作用使得管道车能耗随时间发生振动变化,为此采用平均能耗进行表征该物理量。

图11 管道车运移时平均能耗随管道流量变化图
从图11可知,管道车运移时平均能耗与管道流量呈线性关系。该规律对于进一步预测不同流量条件下管道车运移时的平均能耗具有重要的参考价值。
4 结 论
本文采用流固耦合数值模拟对管道车在平直管段振动运移时的管道内部流场与管道车瞬时响应进行了瞬态分析。主要结论如下:
(1) 对比模拟值与试验值,管道车瞬时速度、管道断面流速和管道沿程测压管水头等水力特性的相对误差均不超过4.8%,二者结论一致,说明流固耦合数值计算模型能够准确得到筒装料管道水力输送的水力特性,为评价管道车的输送效果提供了保证。
(2) 不同时刻的管道车运移过程中的瞬时速度在一定微小范围内振动变化,可以将管道车在平直管段的振动运移视为恒定运动。
(3) 管道车运移时平均能耗与管道流量之间呈线性变化规律。
(4) 管道车向下游运移时,轴向流速分布基本一致,而管道车局部压强却呈现出降低的变化趋势。
(5) 管道车运移时近壁面流场区域出现了“W”型的测压管水头分布。该压强分布与无限域的圆柱绕流流场压强分布有所不同,其中管道车运移时的管道流体动能不仅存在能量耗散,还存在能量转化。因此,管道车运移的能耗损失还需要进一步的深入的研究。

