带弹性膜的部分充液罐车罐体内液体横向晃动的瞬态响应分析
王琼瑶, Subhash Rakheja, 上官文斌
(华南理工大学 机械与汽车工程学院, 广州 510640)
贮箱内液体晃动问题是工程中常见的问题,液罐车,水坝,航天器的燃料贮箱等都存在液体晃动的问题[1-2]。液罐车为液体货物道路运输的最大载体,主要承担石油、液化天然气、危险化学品的运输。由于液体货物密度的不同以及车轴最大载荷的限制等原因,液罐车通常处于部分充液状态。罐车转向时,若行进速度较大,罐体内的液体将大幅度晃动并与罐车相互作用,从而降低了液罐车的侧倾稳定性[3]。事故统计表明,相比较于固体载货车辆,液罐车更容易发生侧翻事故,且造成严重的人员伤亡和财产损失[4]。因此研究液罐车罐体内液体晃动的动态特性以及如何限制液体晃动具有重要的现实意义。
限制罐体内液体晃动的主要方法一般是在罐体内添加隔板[5-7]或者防波板[8-10](带孔的隔板)。Rakheja等采用了准静态模型法研究了隔板的数目对液罐车侧倾极限的影响。研究结果表明隔板能够极大地提高液罐车的侧倾稳定性并减小罐体的部分充液状态。Popov等首次基于全非线性流体动力学方程研究了带隔板的罐体内液体复杂的晃动现象。结果表明,与防波板相比,隔板能使罐车转向时的侧倾力矩减小30%。Wang等对隔板的研究表明,在罐车直线制动过程中,等间距的隔板能使液体货物的纵向载荷转移量最小。刘小民等采用双向流固耦合的方法,对运动罐车在制动过程中罐体内液体的晃动现象进行了数值分析,研究了不同材料的防波板在载液罐体内的受力情况。研究表明,罐体端面受力随着充液比的增大而增加,当充液比为0.8时,罐体的总体受力最大。Kandasamy等研究了传统防波板、部分式防波板以及倾斜式防波板对液体晃动的影响。结果表明,传统防波板在罐车制动过程中能有效抑制液体的纵向晃动,但在罐车转向时对液体的横向晃动影响不大。倾斜式防波板既能抑制液体的纵向晃动,也能抑制液体的横向晃动。尽管隔板或者防波板能够有效限制液体晃动,但它们极大地增大了罐车的结构重量从而减小了运输效率。此外,隔板或者防波板的引入使得罐体内的清洁工作非常困难。
为了限制液体的晃动,一种新的抑制液体晃动的方法是在液体的自由面上覆盖一层弹性膜,弹性膜的边缘固定在罐体的内壁。相比较于隔板或者防波板,弹性膜结构简单,重量轻,能有效提高液罐车的运输效率。Bauer[11]研究了竖直圆柱形罐体内液体晃动的共振频率,其中液体表面覆盖了一层弹性膜,且假设液体为不可压缩无黏性的流体。研究结果表明,流体-弹性膜的耦合频率大于不耦合时液体的晃动频率。随后,Bauer等[12]进一步研究了液体的黏性对流体-弹性膜的耦合频率的影响,结果表明,液体的黏性会进一步增大耦合频率。Parasil等[13-14]采用了任意拉格朗日欧拉方法研究了二维/三维矩形槽内液体晃动的动力学行为,其中液体的自由面覆盖了一层弹性膜。研究结果表明弹性膜本身的非线性特性对液体的晃动的影响非常大。
以上关于弹性膜对液体晃动的影响的研究仅限于竖直放置的罐体,且研究中仅考虑了液体与弹性膜的耦合作用,并没有考虑空气介质。本文建立了流体-弹性膜耦合动力学模型(模型中考虑了空气介质),通过实验验证了模型的有效性。研究了二维水平圆柱形罐体在横向加速度激励下液体晃动的动力学现象。通过对比不带弹性膜的罐体内液体晃动的动力学响应,探究了弹性膜对液体晃动响应的影响。
1 流体-弹性膜耦合动力学模型
为了限制液体的晃动,本文提出了一种新型的抑制液体晃动的装置:弹性膜,即在自由液面上覆盖一层弹性膜,弹性膜的四周固定在罐体的内壁。图1为带弹性膜的液灌模型图。其中,罐体的横截面为圆形,直径为2.03 m。

图1 液体二维横向晃动的流体-弹性膜耦合模型
流体域采用的是二相流模型,即可压缩的气相和轻微可压缩的液相,气相和液相由弹性膜分开。在圆心位置建立笛卡尔坐标系,其中Y轴沿罐体的径向方向,Z轴竖直向上。流体-弹性膜耦合问题是通过将计算流体动力学与流固耦合仿真平台相结合来进行模拟的。在此流固耦合模型中,考虑了两个流固耦合面,即弹性膜的上表面与气相的交界面(流固耦合面1)以及弹性膜的下表面与液相的交界面(流固耦合面2);与液相接触的罐体部分采用壁面边界条件;与气相接触的罐体部分则采用自由边界条件,允许空气自由出入罐体,如图1所示。弹性膜的初始状态假设为无预应力,且其固定于罐体内壁的位置高度为当充液比(液体体积与罐体总体积的比值)为48%时自由液面的位置高度。因此,当充液体积比大于48%时,弹性膜将承受一定的预应力。
考虑到液体的黏性力与惯性力相比非常小,因此在建模中忽略了液体的黏性力。另外,由于液体晃动的过程中弹性膜较大的阻尼作用,导致液体晃动的幅值比较小,因此采用层流模型来模拟液体的晃动。弹性膜结构在ANSYS中被划分成结构网格。流体域的网格划分则通过CFX中的网格自动划分技术完成。由于在弹性膜邻近的网格变形量大,物理量的变化梯度大,因此对弹性膜邻近的网格进行局部网格细化处理。由于是二维分析,垂直于纸面的方向的长度恰好为一个网格单元的长度。
通过对流固耦合模型的动力学响应进行分析,可以确定液体晃动产生的作用在罐体上的力的瞬态和稳态值、液体载荷的转移量以及侧倾力矩的大小。液体载荷转移量是用液体的质心位置相对于液体处于静态时质心位置的变化量来表示的,如图2所示。对流体域进行网格划分(离散化),则流体域液相的质心坐标变化可通过流体域液相的体积积分求得
(1)
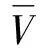
对于单元e,其对罐体壁面产生的作用力可由单元中心的压强Pe与单元的面积矢量Ae求出。因而,液体晃动产生的合力为
(2)
式中:Fi为晃动合力沿i(i=y,z)轴的分量,Aei为单元e的面积矢量沿i轴的投影面积。φ为液相与罐体壁面以及弹性膜的接触区域。

图2 液体的载荷转移量,力以及力矩的计算原理图
侧倾力矩的计算参考点为罐体几何中心点在罐体底部的投影点O′,通过单个单元的力矩在区域φ上的积分求得
(3)
式中:Fe为单元e产生的晃动力矢量,le为单元相对于O′的位置矢量,M为侧倾力矩。
2 模型有效性检验
图3为带弹性膜的罐体实验模型,其中罐体长1.99 m,半径0.268 m。罐体通过支撑架与支撑板固定在振动台上。实验用的液体为水,充液比为50%。

(a) 带弹性气袋的罐体模型实验图

(b) 带弹性气袋的罐体
在实验中,由于气密性的问题,故采用软质PVC材料制成的弹性气袋来替代弹性膜,为了更好地模拟气袋的密闭性,将与空气介质接触的罐体定义为壁面边界,而并非图1所示的开放边界。弹性气袋的横截面结构如图3(b)所示,整个弹性气袋的形状类似于一个半圆柱体(以满足实验中充液体积比为50%的设计要求),长度和半径均与罐体相同,以便于弹性气袋固定在罐体的上圆柱面上。弹性气袋通过尼龙搭扣被初步固定在罐体内壁上,然后通过工业强力胶水对气袋与罐体接触的边缘进行黏贴密封处理,其与液面接触的部分因此可以近似看成是一层弹性膜。
为了验证流体-弹性膜耦合动力学模型的有效性,首先需获得实验中弹性膜的材料参数。为此,对实验用的制成弹性气袋的材料样本在MTS实验台上进行了多次拉伸实验,如图4(a)所示,MTS实验台的拉伸速率恒定为0.1 mm/s。将测试结果取平均值即得到图4(b)的材料样本的应力-应变曲线。

图4 弹性膜材料拉伸实验示意图
从图4中材料的应力-应变曲线关系可以看出,实验用的材料可以看成是超弹性材料。在流固耦合模型中,采用Yeoh超弹性材料模型对弹性膜进行模拟。Yeoh模型主要用来模拟诸如橡胶等轻微可压缩、非线性弹性材料的变形。模型的弹性属性主要用应变能密度函数来表示,应变能密度函数一般用关于应变不变量I1,I2,I3的多项式表示。当模型用来模拟完全不可压缩的橡胶材料时,相应的应变能密度函数仅是关于应变不变量I1的多项式。此时的应变能密度函数可以写成
(4)
其中,应变不变量I1可以写成
(5)
式中:Ci为材料常数,λ1,λ2,λ3是主伸长比。利用ANSYS WORKBENCH中的超弹性曲线拟合工具,将实验得到的材料样本的应力-应变曲线拟合成Yeoh超弹性材料模型。相应的材料常数便可确定:C1=2.310 8 Pa,C2=0.549 6 Pa,C3=0.120 8 Pa。
在实验中,通过对液体横向自由晃动响应进行分析可知,液体横向晃动的固有频率为1.3 Hz。为了验证仿真模型的有效性,需对仿真模型在固有频率处进行验证。图5为实验结果与仿真结果的对比,其中横向加速度激励为ay=0.5sin(2πft),激励频率为1.3 Hz,激励的幅值分别为0.5 m/s2和1.0 m/s2。由于仿真模型是二维模型,因此实验结果和仿真结果均是相对于单位罐体长度后的结果。由图可知,仿真结果和实验结果基本吻合,但在峰值处还是有一些偏差,主要有以下几个原因:① 由于空间狭小,操作不便,弹性气袋边缘与罐体壁面处的黏贴情况在一些地方可能并不牢固;② 实验中,液体晃动的过程中,弹性气袋的气压会发生变化,而在仿真模型中,气压则不会变化。
3 流体-弹性膜耦合动力学模型的仿真分析
以实际液罐车的罐体尺寸为依据,建立了1∶1的简化几何模型。罐体的横截面为圆形,直径为2.03 m,由于是二维分析,垂直于纸面的方向的长度恰好为一个网格单元的长度:0.02 m。在液体的自由面上覆盖一层弹性膜,弹性膜的两端固定在罐体的内壁上,弹性膜的厚度δ为0.005 m。考虑了三种不同的充液体积比进行研究,即50%,65%和80%。液体载荷在不同的充液体积比时的密度并不相同,以保持液体载荷的总重量不变。不同充液体积比下,液体载荷的密度以及代表性的液体,如表1所示。



(a) 横向加速度激励:ay=0.5sin(2πft),f=1.3 Hz

(b) 横向加速度激励:ay=1.0sin(2πft),f=1.3 Hz

由于弹性膜的固定位置为充液高度为当充液比为48%时自由液面的位置高度,因此罐体内的初始充液体积比为48%。这意味着在这三种不同充液体积比的情况下,弹性膜的变形大小将会不同,其预应力的大小也将不同,图6为弹性膜在这三种充液体积比时的变形图。

为了达到目标充液体积比(50%、65%和80%),则需要往罐体内额外注入液体。因此本文中一个完整的仿真模拟一般包含以下两个阶段:
(1) 充液阶段:由于罐体内的初始充液体积比为48%,为了达到仿真模拟所需的50%,65%和80%的充液体积比,需要往罐体内注入额外的液体质量Δm,Δm=ρΔV,ρ为不同充液体积比时液体的质量密度;ΔV为仿真模拟所需的液体体积与罐体内初始液体体积的差值。为了往罐体内注入额外的液体质量,在罐体接近底部的位置设置一个质量点源,通过质量点源流进罐体内的质量流量如图7(a)所示,横坐标表示时间(s),纵坐标表示质量流量(kg/s),曲线与横坐标围成的面积即为往罐体额外注入的液体质量Δm。
(2) 加速度激励阶段:当充液阶段完成后,开始对罐体的流体域施加圆滑过渡的斜坡阶跃加速度激励,如图7(b)所示,其数学表达式为
G(t)=
(6)
式中:G(t)表示加速度激励,k表示上升速率,β表示圆滑过渡参数,一般取值0.2。

图7 一次完整仿真的两个阶段
由于仿真中加速度激励的大小为0.3g,液体晃动时弹性膜的应变不大,由图4(b)可知。且本文提出的模型为二维模型,因此,在应变较小的情况下,弹性膜的杨氏模量可近似为恒定值,以提高计算效率。因此在本文中,弹性膜假设为由具有各向同性的橡胶材料制成,其物理参数如表2所示。

由于在仿真计算中,弹性膜的杨氏模量为一恒定值1×107Pa,因此在液体晃动的过程中,弹性膜的应力σ可以通过其应变ε来求得
σ=E·ε
(7)
在二维分析中,弹性膜的应变即为弹性膜的伸长率—弹性膜的伸长长度ΔL与其初始长度L0的比值
(8)

(i=1,2,…,N,N→∞)
(9)
弹性膜的总长可以由以下表达式计算
(10)

图8 弹性膜的变形示意图
3.1 晃动力和力矩
图9分别为罐体内在有无弹性膜的情况下,横向晃动力的时间历程响应的对比和侧倾力矩的时间历程响应的对比。其中,充液体积比为65%,横向加速度激励圆滑过渡的为斜坡-阶跃加速度激励,大小为0.3g,如图7(b)所示。对比结果表明,罐体内在有无弹性膜的情况下,横向晃动力的峰值和稳态值大小相当(图9(a));但弹性膜使作用在罐体上的侧倾力矩的峰值和稳态均值均大幅减小(图9(b)),主要是因为弹性膜限制了液体自由面的运动,相应地便减小了液体的载荷转移量;此外,通过对液体晃动的稳态响应进行频谱分析可知:在罐体内有无弹性膜的情况下,液体横向晃动的固有频率分别为1.35 Hz和0.62 Hz,说明弹性膜明显增大了液体横向晃动的固有频率。

(a) 横向晃动力

(b) 侧倾力矩
图10和11分别为罐体内在有无弹性膜的情况下,横向力峰值和稳态均值的对比以及侧倾力矩峰值和稳态均值的对比。其中,加速度激励的幅值为0.3g,充液体积比分别为50%,65%和80%。由图可知,弹性膜使作用在罐体上的横向晃动力的峰值和稳态均值均增大了,主要是因为弹性膜限制自由面向上运动,导致聚集的液体对罐体壁面的压强增大。由图10(a)可知,当充液体积比为50%时,弹性膜的初始应力较小,使得自由液面的运动幅值相对较大,自由液面较大幅值的运动反过来又会使弹性膜产生较大额外应力。当充液体积比为65%或80%时,由于弹性膜的初始应力较大,使得自由液面的运动幅值相对较小,自由液面的运动使弹性膜产生的额外应力较小。因此,在有弹性膜的罐体内,充液体积比为50%时,作用在罐体上的横向晃动力的峰值最大。此外,通过对比图10(a)和(b)可知,当充液体积比为65%或80%时,由于弹性膜的初始应力较大,弹性膜产生的额外应力较小,使得横向晃动力的峰值和稳态均值之间的差异较小。

(a) 峰值

(b) 稳态均值

(a) 峰值

(b) 稳态均值
由图11可知,弹性膜使得作用在罐体上的侧倾力矩的峰值和稳态均值均明显减小。主要原因是侧倾力矩受横向和垂向载荷转移量的影响很大,而弹性膜极大地限制了液体晃动时的载荷转移量。以充液体积比为50%的情况为例,图12为罐体内有、无弹性膜的情况下,当充液体积比为50%时,横向和纵向载荷转移量的时间历程曲线。由图可知,在弹性膜的阻尼作用下,液体晃动时的横向和纵向载荷转移量均大幅减小。此外,从时间历程响应曲线可知,弹性膜增大了液体晃动响应的振荡频率,缩短了液体晃动进入稳态时所需的时间。

(a) 横向载荷转移量

(b) 垂向载荷转移量
3.2 晃动频率
对液体自由晃动响应进行频率分辨率为0.01 Hz的快速傅里叶变换即可得到液体晃动的固有频率。当充液体积比的范围在50%~80%时,在带弹性模的罐体内,液体横向晃动的固有频率是不带弹性膜罐体内液体横向晃动固有频率的2倍至2.5倍,如图13所示。当充液体积比从50%增大到80%时,不带弹性膜罐体内液体横向晃动的固有频率增加了15.5%,而带弹性膜的罐体内液体横向晃动的固有频率增加了30%,主要是高充液体积比下,弹性膜的应力值迅速增大引起的。由图可知,在一般充液体积比下,带弹性膜罐体内液体横向晃动的固有频率在1.16~1.51 Hz范围内,而液罐车的紧急转向频率一般在0.6 Hz作用。因此,弹性膜使液体横向晃动的固有频率远离了液罐车的紧急转向频率,从而避免了液罐车紧急转向时共振现象的发生。
3.3 弹性膜的变形分析
图14分别为弹性膜在液体晃动的初始状态、稳态以及弹性膜达到最大变形量时的轮廓图。当充液体积比为50%时,由于弹性膜的应力较小,弹性膜的运动主要受液体运动的影响且弹性膜对液体晃动的影响相对

图13 液体横向晃动的固有频率
较小。因此,在耦合模型中,除了晃动幅值相对较小外,液体的运动方式与晃动模型中液体的运动方式一致。值得注意的是,当晃动达到稳态时,弹性膜关于其初始位置对称。当充液体积比达到65%或者80%时,由于弹性膜的变形量急剧增大,其初始应力急剧增大,使得弹性膜在此变形基础上的进一步变形量非常小,如图14(b)和(c)所示。

(a) 充液体积比:50%

(b) 充液体积比:65%

(c) 充液体积比:80%
图15为弹性膜各个状态下的应力值随充液体积比的变化趋势。由图可知,随着充液体积比的增大,弹性膜的在这三种状态下的应力值都急剧增大,以晃动初始状态时弹性膜的应力值为例,当充液体积比为50%时,弹性膜的初始应力值为0.03 MPa,而当充液体积比为80%时,这个应力值增大到了2.95 MPa,增大了97倍。弹性膜在液体晃动的稳态时、弹性膜变形量最大时的应力值随着充液体积比的变化趋势也与之类似。但是,随着充液体积比的增大,弹性膜的应力值在这三种状态之间的变化却越来越小:当充液体积比为50%时,弹性膜的应力值从液体晃动初始状态时的0.03 MPa到弹性膜变形量最大时的0.68 MPa,应力值的增长率达到了2 167%;当充液体积为65%和80%时,相应的应力值的增长率分别为19.2%和2.0%。

图15 弹性膜在不通充液体积比、不同状态下的应力值
4 结 论
(1) 建立了带弹性膜罐体内液体晃动的流体-弹性膜耦合动力学模型。并通过实验验证了模型的有效性。
(2) 研究了弹性膜及其预应力的大小对液体晃动响应的影响。研究结果表明,弹性膜能限制液体晃动的幅值,从而减小液体晃动对罐体壁面产生的侧倾力矩。
(3) 弹性膜增大了液体横向晃动的固有频率。当充液体积比从50%增大到80%时,不带弹性膜罐体内液体横向晃动的固有频率增加了15.5%,而带弹性膜的罐体内液体横向晃动的固有频率增加了30%。此外,弹性膜使液体横向晃动的固有频率远离了液罐车的紧急转向频率,从而避免了液罐车紧急转向时共振现象的发生。

