基础隔震结构的隔震层刚度参数分析
卢晟,郭玉荣, 2
基础隔震结构的隔震层刚度参数分析
卢晟1,郭玉荣1, 2
(1. 湖南大学 土木工程学院,湖南 长沙 410082;2. 建筑安全与节能教育部重点实验室,湖南 长沙 410082)
基础隔震结构由于隔震层的水平刚度和上部结构的抗侧刚度相差较大,地震作用过程中隔震层消耗大量能量,能够有效地减小上部结构的地震响应,使上部结构处于弹性状态。将基础隔震结构简化为2质点模型,基于简化模型的质点位移函数推导出临界刚度比。采用有限元软件ETABS建立4个不同刚度比的基础隔震结构,并基于IDA方法进行易损性分析,得到倒塌概率曲线。研究结果表明:文中研究的刚度比会影响基础隔震结构发生破坏的形式,且存在最优的刚度比。分析结果可为基础隔震结构设计提供参考。
基础隔震;2质点模型;刚度比;易损性分析

我国地震活动强度大,频度高,而且地震活动范围广,2008年汶川地震的强度远超当时所在地的设防标准。随着隔震建筑在高烈度地区的逐步推广,关于隔震的研究也在不断进步。王栋等[1]基于整体结构的倾覆力矩和隔震支座的拉应力问题提出了基础隔震结构的高宽比限值。苏经宇等[2]提出了隔震结构2质点等效模型。尚守平等[3]研究了基础隔震中上部结构与隔震层刚度比限值。在JGJ 3—2010《高层建筑混凝土结构设计技术规程》[4]中,对楼层的抗侧刚度作出了相关规定,即本层与相邻上层的刚度比值不宜小于0.7,与相邻上部3层刚度平均值的比值不宜小于0.8。但此项条文是针对非隔震结构,而基础隔震结构的特点就是利用隔震层相对上部结构较小的水平刚度把地震能量大部分消耗在隔震层,故此项条文不适合用于指导隔震结构的隔震层刚度的设计。为此,对隔震层刚度与上部结构刚度之间的关系进行研究,为基础隔震结构设计提供相关参考。
1 基础隔震结构破坏方式
关于基础隔震结构,其破坏形式大致可分为3类:1) 支座拉压应力超过规定限值,结构发生整体倾覆;2) 上部结构相对位移过大,结构进入非线性,发生弹塑性破坏;3) 隔震支座相对位移超过规定限值,隔震支座失效,隔震层发生破坏导致整体结构失效。第1种破坏形式主要由结构的高宽比[1]控制;后2种破坏形式均与位移有关,究竟是上部结构先破坏还是隔震层先破坏主要由两者的刚度关系控制,即刚度协调问题。
2 基础隔震结构简化模型
2.1 2质点模型
将基础隔震结构简化为2质点模型,即将上部结构等效为单自由度体系与隔震层组成2质点模型。可以假定:1) 多自由度体系位移按假定形状;2) 基底剪力相等;3) 外力做功相等。
根据假定1,上部结构多自由度质点位移可表示为:
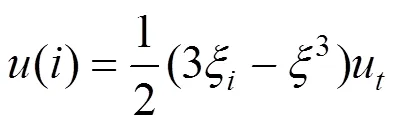
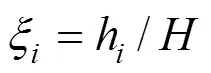
式中:u为结构顶点位移;h为任意截面高度;为结构总高度。
根据假定2和3,可得到的公式有:
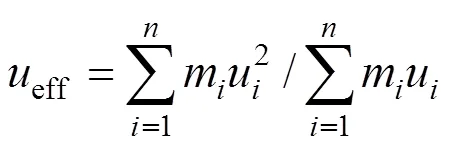
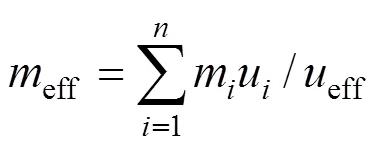
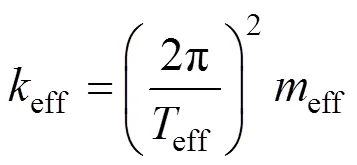
式(3)~(5)中:eff为等效位移;eff为等效质量;eff为等效刚度;eff为等效周期,可由位移反应谱[5]求得。
2.2 刚度比及质量比定义
2.3 运动方程
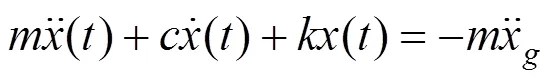
式中:
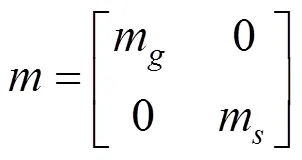
由结构动力学双自由度频率公式可求得:
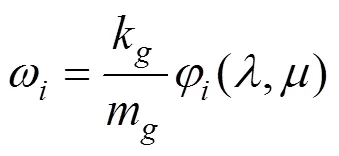
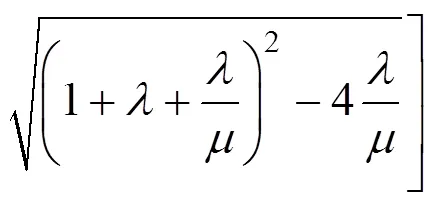
式中:=1,2。
2.4 2质点位移函数
苏经宇等[2]建议对于上部结构平立面规则的隔震建筑,其基底剪力可写为:
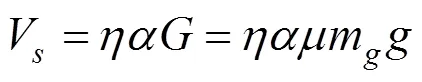
式中:为地震作用匹配系数;为水平地震影响系数;为重力加速度。
根据尚守平等[3]研究,隔震层的剪力可近似取为1+1/倍上部结构地震作用力,即为:
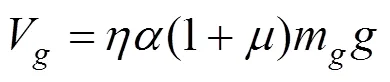
由式(7),(9)和(10)可得上部结构和隔震层的位移函数:
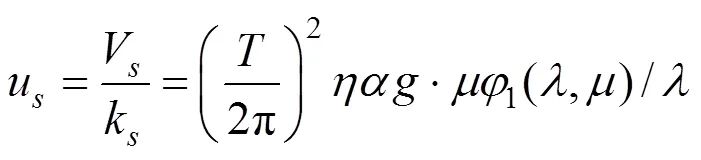
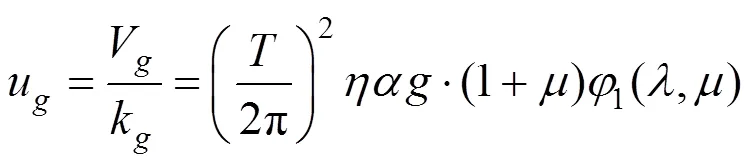
在式(11)和(12)中,令:
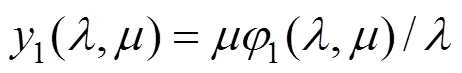
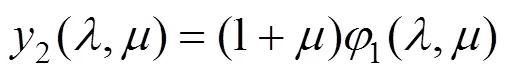
经过计算,取不同的和值,式(13)和(14)之和约恒等于1,则上式可写为:
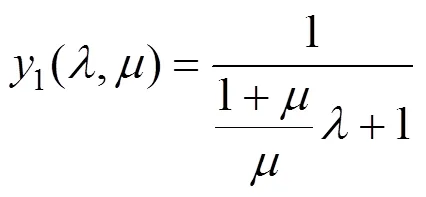
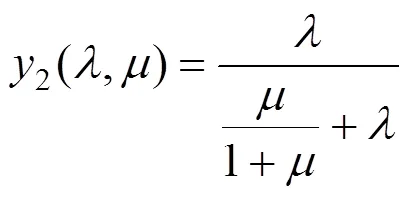
2.5 刚度比限值
由抗震规范[6]可知,基础隔震体系的上部结构和隔震层都有其位移限值条件,对于上部结构:
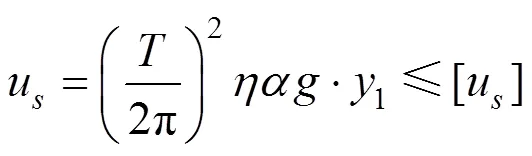
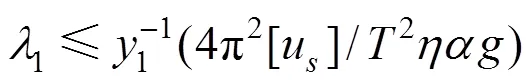
对于隔震层:
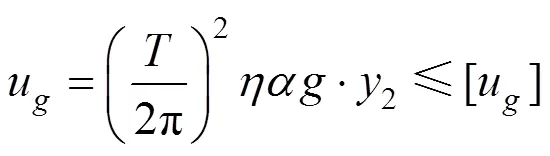
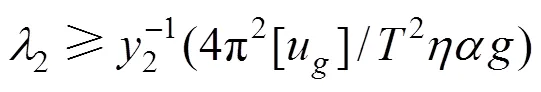
可设想,当刚度比大于某一临界值时,结构破坏由隔震层控制,反之则由上部结构控制。而当等于这个临界值时,上部结构和隔震层同时达到极限状态,此临界值设为λ。
当1=2时,即为上部结构和隔震层同时达到极限位移,可求得:
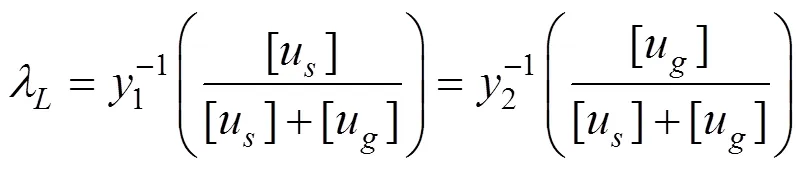
2.6 位移限值
2.6.1 上部结构的位移限值[u]
对于钢筋混凝土结构,Priestley等[7-8]用直接基于位移的方法,以层间位移角为控制条件,得出了结构某高度处的位移函数表达式,并且建议框架结构等效质点的位移为0.65u(u为结构顶层相对 位移)。
文献[9]中建议结构顶点屈服位移取/180~/220(为结构高度)。综上,可得到上部结构位移限值[u]。
2.6.2 隔震层的位移限值[u]
抗震规范表明隔震支座的水平位移,应符合下列要求:
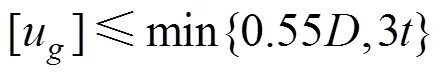
式中:为隔震支座有效直径;为隔震支座橡胶总厚度。
3 基础隔震结构分析模型
3.1 工程概况
本案例为4层钢筋混凝土基础隔震结构,隔震支座采用铅芯叠层橡胶支座。建筑物平面呈矩形分布,其平面尺寸为30 m×12 m,每层层高3.6 m,隔震层1.6 m,沿向的主梁间设置单根次梁。框架柱尺寸为500 mm×500 mm,主梁尺寸为500 mm×300 mm,次梁尺寸为450 mm×300 mm,板厚120 mm,混凝土等级为C30,梁柱纵筋为HRB335,梁柱箍筋为HPB300。该建筑抗震设防类别为乙类,设防烈度为8(0.2)度,场地类型为Ⅲ类场地,设计地震分组为第2组。每根框架柱与基础连接处均设置隔震支座,结构平面布置图如图1 所示。

图1 结构平面布置图
3.2 有限元模型
采用通用有限元软件ETABS建立基础隔震结构的三维空间模型。用ETABS自带的Rubber Isolator连接单元模拟隔震支座,并考虑支座2个水平方向的非线性属性。
经过试算,得到隔震支座最小直径不得小于319.4 mm,故选取的支座型号为LRB350,LRB400,LRB600和LRB1000,支座具体参数见表1。按章节2方法等效的上部结构相关参数见表2。
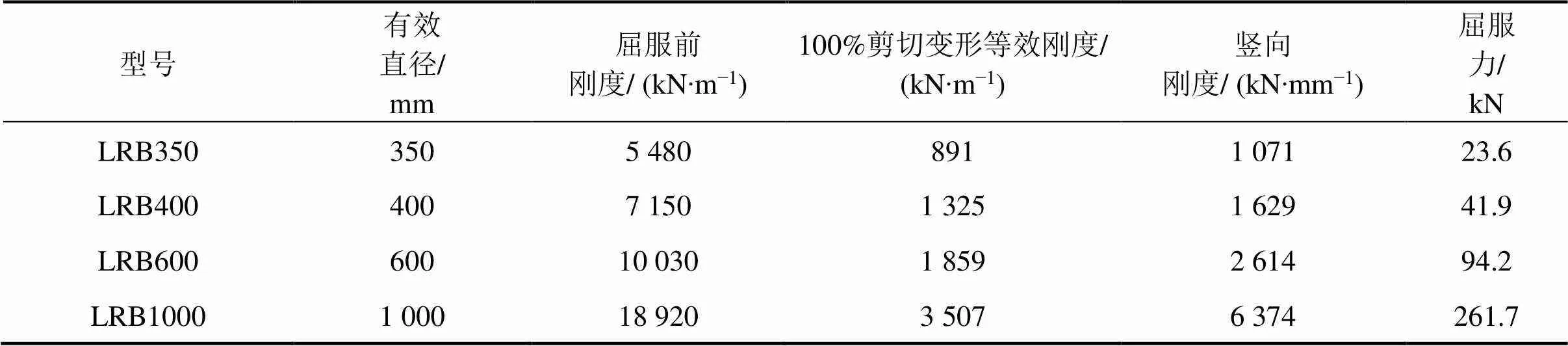
表1 支座参数

表2 等效参数

表3 刚度比与质量比

表4 不同隔震方案的结构周期
本文设计了4种隔震层支座方案,为便于比较,每种隔震方案的隔震层支座都选择同一种类型,以此得到的上部结构等效参数与隔震层相关参数的比值如表3。4种不同刚度比隔震方案的结构前3阶周期如表4。
4 结构地震倒塌易损性分析
4.1 基于IDA的地震倒塌概率分析及评价指标
基于IDA方法的结构倒塌易损性分析,是通过记录在不同地震动强度指标下,使结构发生倒塌的地震动条数collapse和选取的地震动的总数total之比[10]即结构的倒塌概率P为:
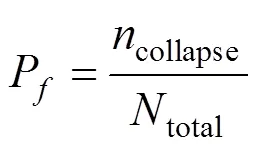
如果结构在某一地面运动强度下(本文取PGA),有50%的地震波输入使结构发生了倒塌,则该地震动强度就是结构体系的平均抗倒塌能力。将此地震动强度和结构的设计大震强度比较,就可以得到结构的倒塌储备系数[11],即
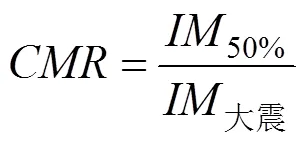
反映了结构抗倒塌能力的相对量,越大,则说明结构抗倒塌能力越强,该指标为结构的性能评价提供了一个比较科学的标准。
4.2 隔震结构性能水准和性能指标
关于基础隔震结构在地震作用下的性能水准划分和性能指标的量化,目前研究还不是很成熟。为方便对比隔震层刚度对结构性能的影响,在参考文献资料[12−13]后,将基础隔震钢筋混凝土框架结构的性能水准定为4个阶段,选取上部结构层间位移角作为性能指标,并确定相应的损伤限值,列于表5。

表5 基础隔震结构性能水准和指标限值
4.3 IDA分析
采用地震动峰值加速度PGA作为地震动强度指标,选取FEMA P695推荐的22条远场地震[11]记录。每条地震动按PGA调幅,1以内调幅步长为0.1,大于1步长为0.2,调幅后的PGA为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.2,1.4,1.6,1.8和2。为使结构损伤更符合结构在地震过程中的真实情况[14−15],将地震动水平双向输入,保持2方向输入的地震动强度之比为1:0.85。
这样得到基础隔震结构在各级地震动强度作用下上部结构的最大层间位移角max。每种刚度比的隔震结构得到的数据点有330个。
4.4 结构倒塌判别
在地震作用下,由于隔震结构的隔震层侧移刚度比上部结构侧移刚度小很多,出现大变形的往往在隔震层,而上部结构基本上为弹性响应,隔震层耗散了绝大部分地震输入能量,所以倒塌判定指标的选取要综合考虑上部结构和隔震层的变形。为了体现隔震结构的特点,本文将隔震层变形和上部结构最大层间位移角同时作为判定结构倒塌的依据,只要其中一点超过其极限值,即判定结构倒塌。隔震支座的极限变形如表6。

表6 支座极限变形
4.5 倒塌概率曲线形成
当隔震层刚度较小的时候,在某些地震强度作用下,可能出现隔震支座位移已经超过限值,但是此时对应的上部结构层间位移角并没有超限,而在隔震层刚度较大时,上部结构层间位移角超限时,隔震支座位移仍然处于安全范围,从而造成对基础隔震结构性能的误判。由于易损性分析无法在一条易损性曲线中同时选择隔震层变形和上部结构层间位移角作为控制指标,所以只用单一的易损性曲线评价基础隔震结构的抗震性能难免会有局限性,而倒塌易损性分析可以综合考虑上部结构层间位移角和隔震支座的位移,是评价隔震结构性能更合理的方法。
地震动强度指标仍然选择PGA,地震波输入方向和调幅均和前文一致。结合支座的最大位移和支座极限变形(表6)、上一章节得到的上部结构层间位移角和性能指标限值(表5),可得到在某个地震动强度条件下,22条地震波中使结构发生倒塌的地震动条数。经计算拟合可得到4种刚度比的隔震方案条件下,破坏发生部位百分占比如图2,以及结构倒塌概率曲线如图3。
4.6 倒塌概率曲线分析
从4种隔震方案的破坏占比图(图2)所示,方案1和方案2在地震动强度分别为0.6和0.7时,破坏部位只有隔震支座,随着地震动强度加大,上部结构逐渐出现破坏,方案1上部结构破坏的最高占比在地震动强度为1.6时达到68.4%,即在输入的22条地震波中有将近70%使方案1的上部结构发生破坏;方案3直到地震动强度达到1.4时才出现支座破坏,支座破坏最高占比在1.6时达到30.7%,方案4没有出现支座破坏,是由上部结构破坏造成结构失效。造成此现象的原因在于隔震层和上部结构的相对刚度关系。方案1和方案2由于隔震层刚度相对较小,在地震作用下,隔震层耗散的能量多,隔震层位移较大,造成隔震支座失效从而使结构破坏;方案3和方案4的隔震层刚度相对较大,故上部结构耗散的地震能量占比加大,造成了主要由上部结构控制的结构破坏。
从倒塌概率曲线图3可看出,当PGA<0.6时,4种方案的倒塌概率曲线区别不大;当PGA>0.6时,在相同地震动强度下,方案1和方案4的倒塌概率明显比方案2和方案3要大。由于在这4种方案抗震设防大震对应的PGA均为0.4,而方案1和方案4的50%倒塌概率对应PGA为1g,方案2的PGA50%为1.3,方案3的PGA50%为1.4,从而可以确定4种方案的抗倒塌安全储备CMR。方案1为2.5,方案2为3.25,方案3为3.5,方案4为2.5。
根据式(21)介绍的临界刚度比定义,可算得4种方案的临界刚度比为:方案1λ=4.4;方案2λ=5.0;方案3λ=7.5;方案4λ=11.1。对比表3中实际结构的刚度比可知,方案1和方案4的实际刚度比与建议的临界刚度比相差较大,说明隔震层刚度过小或过大;方案2和方案3与临界刚度比较接近,其中方案2的刚度比实际值和建议值最为接近。
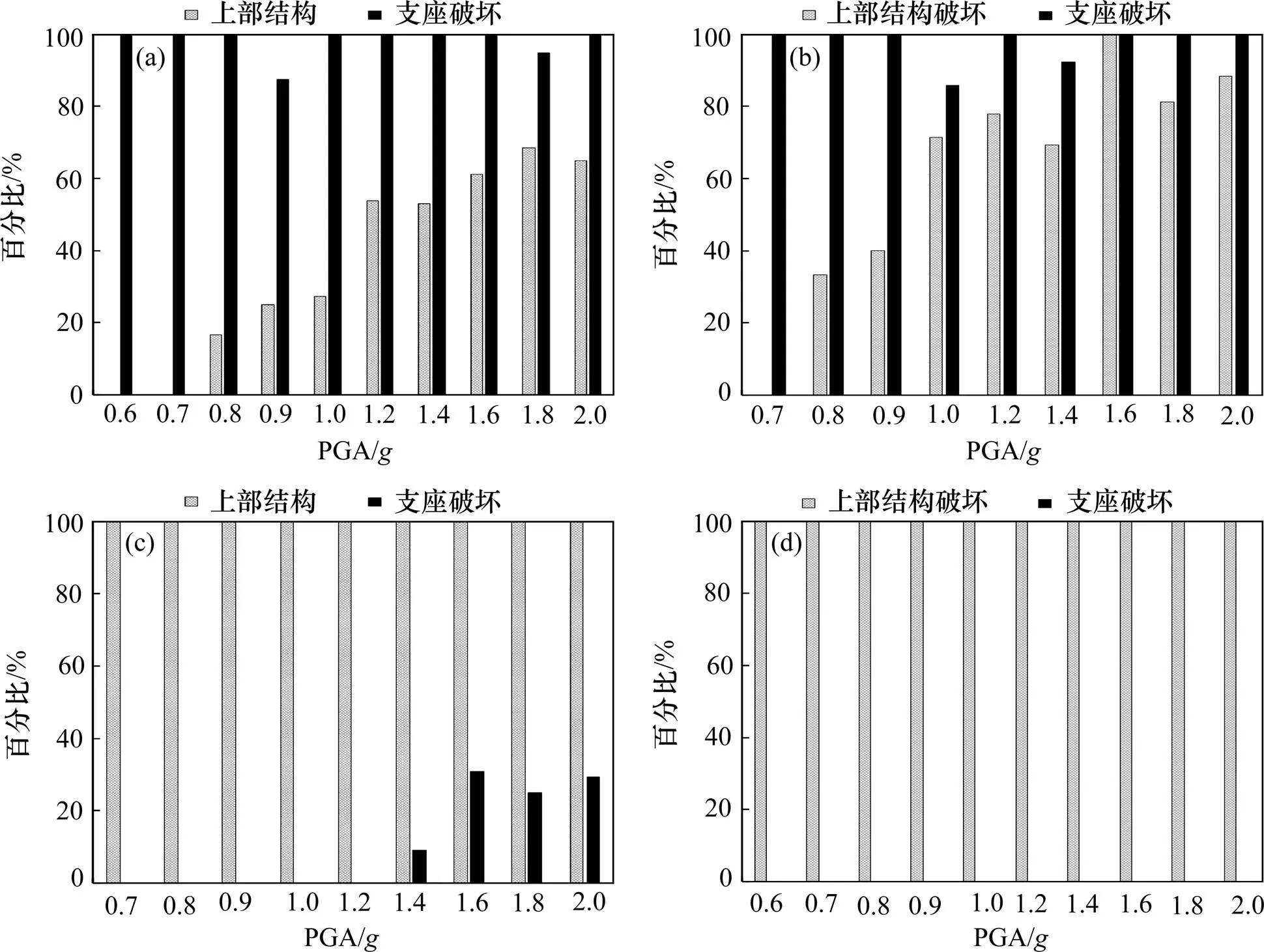
(a) 方案1的破坏部位占比;(b) 方案2的破坏部位占比;(c) 方案3的破坏部位占比;(d) 方案4的破坏部位占比
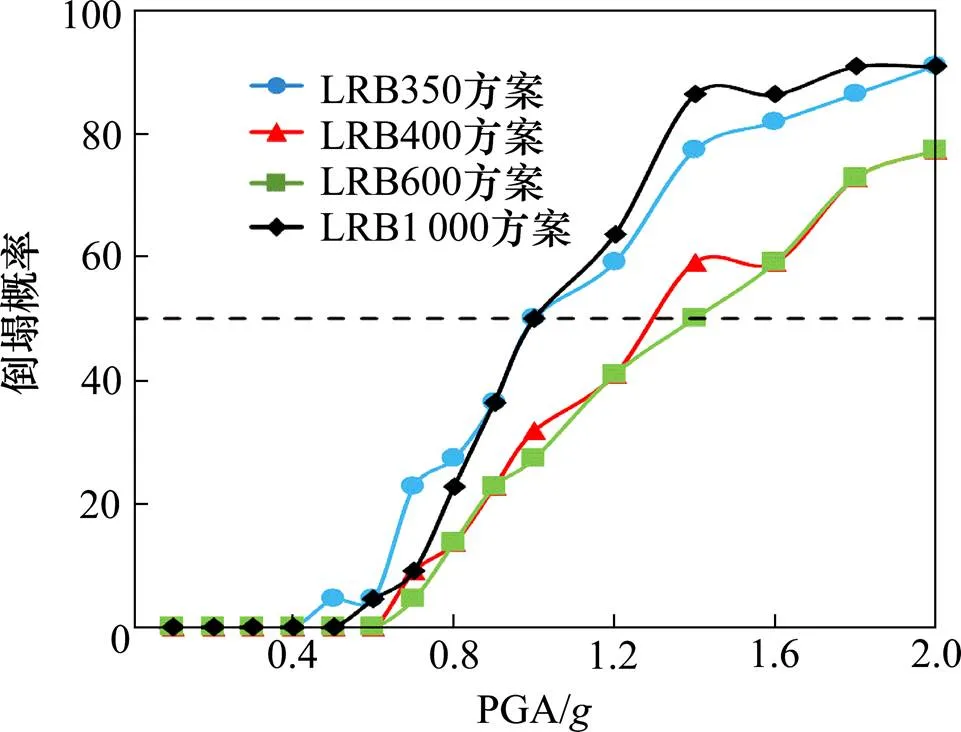
图4 结构倒塌概率曲线
总而言之,4种隔震方案都实现了大震不倒,方案2和方案3的倒塌概率相对较小,而且抗倒塌安全储备系数较大,抗倒塌能力较高。方案3的结构破坏主要由上部结构控制,隔震层基本没有发挥性能,失去了隔震的意义。
故方案2,即隔震层与上部结构等效刚度比值为6.4时,能够充分利用隔震层,抗震性能较高,且经济性更好,是更为合理的方案。
5 结论
1) 基础隔震结构上部结构和隔震层的刚度比控制着上部结构和隔震层各自的位移,会影响结构发生破坏的形式。
2) 基础隔震结构存在一个使得上部结构和隔震层同时达到位移限值的临界刚度比λ,能够最大限度的利用结构的性能,结构设计时可参考此值来选取相关参数。
3) 基础隔震结构性能评价需要综合考虑隔震层和上部结构,如果仅通过基于上部结构位移角得到的易损性曲线无法全面评价结构抗震性能,倒塌易损性分析综合考虑了上部结构位移角和隔震层的位移,是对基础隔震结构性能评价更合适的 方法。
[1] 王栋, 吕西林, 刘中坡. 不同高宽比基础隔震高层结构振动台试验研究及对比分析[J]. 振动与冲击, 2015, 34(16): 109−118. WANG Dong, LÜ Xilin, LIU Zhongpo. Shaking table test and comparison analysis for base-isolated high-rise buildings with different aspect ratios[J]. Journal of Viberation and Shock, 2015, 34(16):109−118.
[2] 苏经宇, 韩淼, 周锡元, 等. 橡胶支座基础隔震建筑地震作用实用计算方法[J]. 振动工程学报, 1999(2): 82− 89. SU Jingyu, HAN Miao, ZHOU Xiyuan, et al. Practical calculation method for seismic action of base-isolated buildings with rubber bearings[J]. Journal of Vibration Engineering, 1999(2): 82−89.
[3] 尚守平, 王彦. 基础隔震结构中上部结构与隔震层的刚度比限值研究[J]. 建筑结构学报, 2018, 39(3): 48−55. SHANG Shouping, WANG Yan. Study on limit of stiffness ratio between upper structure and isolation layer in base isolation structure[J]. Journal of Building Structures, 2018, 39(3): 48−55.
[4] JGJ 3−2010, 高层建筑混凝土结构技术规程[S]. JGJ 3−2010, Technical specification for concrete structures of tall building[S].
[5] 梁兴文, 谢俊强. 钢筋混凝土框架结构基于位移的实用抗震设计方法[J]. 建筑结构, 2006, 36(增1): 659−662. LIANG Xingwen, XIE Junqiang. Research on displacement-based seismic design method of RC frames[J]. Building Structure, 2006, 36(Suppl 1): 659− 662.
[6] GB 50011—2010, 建筑抗震设计规范[S]. GB 50011—2010, Code for seismic design of buildings[S].
[7] Priestley M J N, Kowalsky M J. Direct displacement- based seismic design of concrete buildings[J]. Bulletin of New Zealand National Society for Earthquake Engineering, 2000, 33(4): 421−444.
[8] Tjen N Tjhin, Mark A Aschheim, John W Wallace. Yield displacement-based seismic design of RC wall buildings[J]. Engineering Structures, 2007(29): 2946− 2959.
[9] 罗文斌, 钱稼茹. 钢筋混凝土框架基于位移的抗震设计[J]. 土木工程学报, 2003, 36(5): 22−29. LUO Wenbin, QIAN Jiaru. Displacement-based seismic design for RC frames[J]. China Civil Engineering Journal, 2003, 36(5): 22−29.
[10] CECS 392:2014, 建筑结构抗倒塌设计规范[S]. CECS 392:2014, Code for anti-collapse design of building structures[S].
[11] FEMA. Quantification of building seismic performance factors (FEMA-P695)[P]. Federal Emergency Management Agency, Washington, D C, 2009.
[12] 杜永峰, 王光环. 基础隔震钢筋混凝土框架结构的性能水准划分与量化分析[J]. 工程抗震与加固改造, 2013, 35(6): 87−92, 97. DU Yongfeng, WANG Guanghuan. Performance levels classification and performance index quantitative analysis of base-isolated RC frame[J]. Earthquake Resistant Engineering and Retrofitting, 2013, 35(6): 87−92, 97.
[13] 杜永峰, 白永利. 考虑近断层地震运动特性的隔震结构抗震性能分析[J]. 工程抗震与加固改造, 2017, 39(2): 78−84. DU Yongfeng, BAI Yongli. Seismic performance analysis of base-isolated structure considering the movement characteristics of near-fault ground motion[J]. Earthquake Resistant Engineering and Retrofitting, 2017, 39(2): 78− 84.
[14] 周长东, 田苗旺, 张许, 等. 考虑多维地震作用的高耸钢筋混凝土烟囱结构易损性分析[J]. 土木工程学报, 2017, 50(3): 54−64. ZHOU Changdong, TIAN Miaowang, ZHANG Xu, et al. Seismic fragility analysis for high-rise RC chimney considering multi-dimensional seismic actions[J]. China Civil Engineering Journal, 2017, 50(3): 54−64.
[15] Hosseinpour F, Abdelnaby A E. Fragility curves for RC frames under multiple earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2017, 98(7): 222−234.
Analysis of stiffness parameters of seismic layer of base isolation structure
LU Sheng1, GUO Yurong1, 2
(1. School of Civil Engineering, Hunan University, Changsha 410082, China; 2. Key Laboratory of Building Safety and Energy, Ministry of Education, Changsha 410082, China)
In the base-isolated structure, due to the large difference between the horizontal stiffness of the isolation layer and the stiffness of the upper structure, the seismic isolation layer consumes a large amount of energy in the process of seismic action, which can effectively reduce the seismic response of the superstructure and keep the upper structure in elastic state. The base isolation structure was simplified into a two-particle model, and the critical stiffness ratio was derived based on the mass displacement function of the simplified model. Four base-isolated structures with different stiffness ratios were established by using the finite element software ETABS, and vulnerability analysis was performed based on the IDA method to obtain collapse probability curves.The results show that the stiffness ratio studied in this paper will affect the damage form of the base isolation structure and there is an optimal stiffness ratio. The analysis results can provide reference for the design of the base isolation structure.
base isolation; two-mass model; stiffness ratio; vulnerability analysis
P315.9;TU311.3
A
1672 − 7029(2019)09− 2290 − 07
10.19713/j.cnki.43−1423/u.2019.09.021
2018−12−06
国家自然科学基金资助项目(51878259,51468010)
郭玉荣(1970−),男,浙江青田人,教授,博士,从事结构抗震研究;E−mail:yurongguo@hnu.edu.cn
(编辑 涂鹏)

