基于桩土界面摩擦特性和桩周土体应力状态的基桩极限侧阻力分析

刘卡伟， 邓少华

(1.湖南省地质矿产勘查开发局416队，湖南 株洲 412007； 2.湖南省地质工程勘察院，湖南 株洲 412003)

0 引言

相应于桩顶作用极限荷载，桩身侧表面所发生的岩土阻力为桩的极限侧阻力[1]，极限侧阻力作为基桩竖向承载力的一部分，其作用机理和计算方法历来受到广大研究人员的重视，现有研究多对桩土界面摩擦特性或从摩擦特性的角度对剪切荷载传递进行研究，如李永辉等[2]开展了桩土界面摩阻特性试验，许宏发等[3]分析了桩土界面单元参数，王卫东等[4]和姚文娟等[5]分析了桩土的剪切荷载传递规律。桩土界面摩擦特性影响了基桩荷载向桩周土体的传递，进而会对桩周土体抗剪强度的发挥产生影响，其是影响基桩极限侧阻力的一个重要因素。

基桩荷载传递到桩周土体中，土体内部会产生剪应力[6]，高俊合等[7]则通过单剪试验研究了试验过程中土与混凝土接触面的剪切破坏带内土体自身的剪切变形。这些都说明伴随着桩侧阻力的发挥，桩周土体抗剪强度开始调动，应力状态开始变化，当土体应力状态满足库伦定律[8]时，桩周土发生剪切破坏，其不能继续承担荷载，故基桩极限侧阻力也受到桩周土体应力状态的影响。

综上所述，桩土界面摩擦特性和桩周土体自身应力状态是影响基桩极限侧阻力的两个因素。本文利用文献[9]的相关分析，推导出基于桩周土体应力状态的土体内部沿桩土界面方向的抗剪强度计算模型，并结合基于桩土界面摩擦特性的界面抗剪强度计算模型。通过对比界面抗剪强度和土体抗剪强度，分析了两种不同剪切破坏模式下基桩极限侧阻力与土体抗剪强度和界面抗剪强度之间的关系，得出了基于界面摩擦特性和土体应力状态的基桩极限侧阻力的计算模型，并通过上海某工程算例进行了计算验证，证明了该模型的合理性和可行性，同时通过该模型分析了不同类型的桩周土的土体抗剪强度和界面抗剪强度随埋深的分布规律，进而得出了极限侧阻力随埋深的分布规律。

算例的计算结果也进一步验证了文献[9]中的相关结论：因内摩擦角和侧压力系数之间的不同关系，极限侧阻力随深度表现出不同的分布特点，在特定关系下，极限侧阻力的分布存在一个临界深度，超过该深度极限侧阻力维持在一个稳定值甚至会不断减小直至为零。

1 基于桩周土体应力状态的沿桩土界面的土体抗剪强度

1.1 单层均质土体埋深z处的的抗剪强度

根据文献[9]的相关分析，图1为桩侧地面以下深度z处的一单元土体的应力状态，该土体顶面竖直方向和侧面水平方向的法向应力分别为：

σ1=γz和σ2=γzξ

式中：γ——土的重度，kN/m3；z——单元土体的埋深，m；ξ——土的静止侧压力系数。

基桩承载后，单元土体的应力状态变化见图2，不考虑侧压力系数在这个过程中的变化，则单元土体的莫尔应力圆在圆心未发生移动的基础上其直径不断变大，直至应力圆与抗剪强度包线相切，应力圆由初始状态变化到极限状态。

图1 桩侧土体的应力状态

图2 应力状态变化过程

结合抗剪强度包线方程和应力圆方程并考虑应力圆达到极限状态时与抗剪强度包线之间的几何关系，可得到单层均质土体埋深z处的的抗剪强度为：

(1)

式中：c——土的粘聚力，kPa；φ——土的内摩擦角，(°)。

1.2 多层非均质土体第i层土埋深z处的抗剪强度

当桩周土体为多层非均质土体时，计算出第i层土埋深z处的竖向应力，即可通过式(1)计算出第i层土埋深z处的沿桩土界面的抗剪强度：

(2)

(3)

式中：ci——第i层土的粘聚力，kPa；φi——第i层土的内摩擦角，(°)；ξi——第i层土的侧压力系数；σvz——第i层土埋深z处的竖向有效应力，kPa；γi、γm——第i层土和其上第m层土的的重度，地下水位以下取浮重度，kN/m3；Δzm——第m层土的厚度，m。

2 基于桩土界面摩擦特性的界面抗剪强度

桩土界面抗剪强度伴随着界面剪切变形的发展而不断发挥，其反映了桩和土这两种不同材料接触面抵抗相对位移的能力，具有摩擦特性，故可应用摩擦定律来表达。表达式如下：

τii(z)=σvzξitanδi

(4)

δi=αφi

(5)

式中：δi——第i层土的桩土界面摩擦角，(°)；α——折减系数，与桩侧表面粗糙程度和桩周土透水性有关，参考《建筑地基基础设计规范》(GB 50007-2011)[10]表6.7.5-1，可根据桩侧表面粗糙程度和桩周土透水性取1/3～1。

3 极限侧阻力的计算

对比前文所述的土体抗剪强度和界面抗剪强度，可以将基桩侧阻力达到极限值时的破坏模式分为以下两种情况。

当τi<τs时，随着基桩荷载的增加，桩土界面剪切应力会先于桩周土体达到极限值，桩土界面发生相对滑动，桩周土体还未剪切破坏，此时基桩极限侧阻力等于界面抗剪强度，改善桩土界面摩擦特性将有助于基桩侧阻力的提高。

当τi>τs时，随着基桩荷载的增加，桩周土体会先于桩土界面达到极限平衡，桩周土体发生剪切破坏，因界面摩擦作用，基桩会带动桩周部分土体一起向下滑动，桩土界面未发生相对滑动，此时基桩极限侧阻力等于土体抗剪强度，改善桩土界面摩擦特性对基桩侧阻力的提高帮助不大。

基于以上分析，并借鉴地基沉降计算的分层总和法，将桩周土划分为若干水平土层，各土层厚度分别为Δz1、Δz2、Δz3、…、Δzn，然后利用式(1)计算出每层土的层顶面和层底面的竖向应力，并用式(10)计算出该两竖向应力的平均值作为该层土的平均竖向应力，代入式(9)，计算出每一层土的沿桩土界面的抗剪强度，并与界面抗剪强度进行比较，取两者的小值为该层土的极限侧阻力，再累加可得总极限侧阻力，计算公式如下：

(6)

qsik=min(τsi,τii)

(7)

(8)

(9)

(10)

(11)

为保证计算精度，分层应考虑以下因素：

(1)分层厚度不能太厚；

(2)不同的土层的界面，因重度、抗剪强度、侧压力系数不同应为分层面；

(3)地下水位应为分层面。

4 算例验证与分析

4.1 算例概况与计算结果

以上海中心大厦工程项目[11]作为算例，并结合其SYZB01试桩结果进行分析，试桩桩径1000 mm，采用堆载法加载，总桩长88 m，上部桩长25 m采用双层套管与桩周土层隔离，有效桩长63 m。笔者在excel中利用函数来表达公式(6)～(11)，计算出每个分层的分层界面抗剪强度，再通过对每一类土的分层厚度的加权平均计算出每类土的土层极限侧阻力。考虑到桩端进行了后注浆，桩端以上一定范围内的桩土界面摩擦特性有所改善，粉砂夹中粗砂⑨2-1和砂质粉土⑨1的界面摩擦角折减系数取0.64，其它土层根据透水性取0.42～0.50，各土层的侧压力系数参考文献[12]取值。试桩桩周土的力学参数和试桩结果以及计算分层情况和侧阻力计算结果见表1。通过对比，有效桩长范围内，各类土的土层极限侧阻力的计算值与测试值的比值为0.71～1.16，均方差为0.166；总极限侧阻力的计算值为22920 kN，总极限侧阻力的测试值为24175 kN，计算值与测试值的比值为0.948，计算结果和测试结果比较接近。

4.2 界面摩擦特性和土体应力状态对侧阻力的影响

将每一类土层的每个分层的界面抗剪强度和土体抗剪强度按照分层厚度进行加权平均计算，计算出每一类土层的界面抗剪强度和土体抗剪强度进行比较，计算结果见表2。

表1 SYZB01试桩主要指标和侧阻力计算

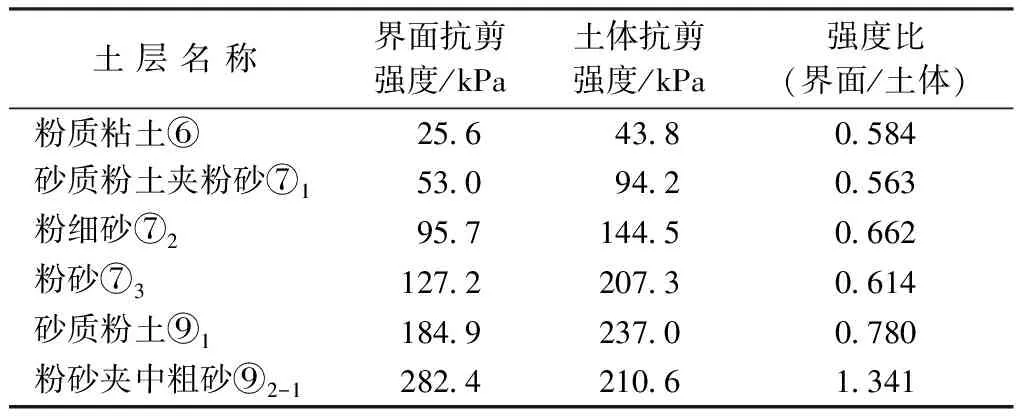
表2 界面和土体抗剪强度

砂质粉土⑨1和粉砂夹中粗砂⑨2-1因桩端后注浆使得桩土界面摩擦特性改善，其中粉砂夹中粗砂⑨2-1的界面摩擦作用使土体应力状态达到极限平衡，土体强度得到充分发挥，砂质粉土⑨1受注浆影响，其土体抗剪强度发挥了78%。其它土层则因桩土界面强度不足而没能充分调动土体强度，土体抗剪强度仅发挥了56%～66%，影响了基桩侧阻力的发挥。

由以上分析可知，基桩极限侧阻力的发挥受到桩土界面摩擦特性和桩周土体应力状态的共同作用影响，良好的界面摩擦特性能够使桩周土体应力状态达到极限平衡状态，土体强度被充分调动，从而使基桩侧阻力得到最大发挥，故对于摩擦型基桩采用后注浆或减小桩周泥皮厚度等措施改善桩土界面摩擦性能对于提高基桩侧阻力有重要意义。

4.3 土体抗剪强度随埋深的分布

为分析土体抗剪强度随桩周土埋深的变化规律，将算例中试验桩在桩周深度0～65.5 m的桩周土分别假定为淤泥质粘土④、粘土⑤1a、粉质粘土⑥和粉细砂⑦2这4种情况，用前述的极限侧阻力计算方法分别计算这4种情况下基桩0～65.5 m深度范围内的土体抗剪强度，计算参数见表3，计算结果见图3。

表3 计算参数

粉细砂⑦2的土体抗剪强度随深度线性递增；淤泥质粘土④的土体抗剪强度先随深度非线性递增，然后递增速率不断减小并趋近于一定值，即由非线性递增逐渐过渡为线性递增；粘土⑤1a的土体抗剪强度先随深度非线性递增，然后递增速率不断减小并趋近于零，即由非线性递增逐渐过渡为一稳定值；粉质粘土⑥的土体抗剪强度先随深度非线性递增，在某一深度处开始随深度呈非线性递减，最终在某一深度处减小为零，并且从该深度开始将一直为零。

图3 土体抗剪强度随埋深的变化曲线

这4种桩周土的土体抗剪强度随深度的变化各不相同，是因为它们的内摩擦角和侧压力系数之间具备不同的关系。

根据文献[9]的分析，粉细砂⑦2为无粘性土，其内摩擦角和侧压力系数满足sinφ>(1-ξ)/(1+ξ)，其土体抗剪强度对深度的导数始终大于零，故土体抗剪强度随着埋深增大而呈线性递增，土体抗剪强度随埋深呈三角形分布。

淤泥质粘土④这类粘性土属于Ⅰ类粘性土，其内摩擦角和侧压力系数满足sinφ>(1-ξ)/(1+ξ)，土体抗剪强度对深度的导数也始终大于零，但导数随深度增加具有一个确定的极限值，该极限值不为零，故土体抗剪强度随着埋深增大而呈非线性递增，递增速率将不断减小且最终趋近于某一非零定值，该定值与重度、侧压力系数和内摩擦角有关，该类粘性土的土体抗剪强度随埋深呈上部近似三角形+下部近似梯形分布。

粘土⑤1a属于Ⅱ类粘性土，其侧压力系数与内摩擦角满足sinφ=(1-ξ)/(1+ξ)，其土体抗剪强度对深度的导数始终大于零，但该导数随深度的极限值为零，故土体抗剪强度随着埋深增大而呈非线性递增，递增速率将不断减小且最终趋近于零，该类粘性土的土体抗剪强度随埋深呈上部近似三角形+下部近似矩形分布。

粉质粘土⑥这类粘性土属于Ⅲ类粘性土，因其侧压力系数与内摩擦角满足sinφ<(1-ξ)/(1+ξ)。土体抗剪强度对深度的导数先大于零，到达某一深度后该导数小于零，且随着埋深的继续增加将一直小于零。说明该类粘性土的土体抗剪强度随埋深先不断增大然后不断减小并最终减小为零。

同时通过图3，可以分析得出粘聚力和内摩擦角对于土体抗剪强度的不同作用：粘聚力主要影响了浅层土体抗剪强度，能够给浅层土体抗剪强度一个初始值，粘聚力越大，该初始值越大，对于无粘性土，浅层土体抗剪强度几乎为零；内摩擦角则影响了深层土体抗剪强度，其与侧压力系数的不同关系决定了土体抗剪强度在深层土体中随埋深的变化规律。

4.4 界面抗剪强度和极限侧阻力随埋深的分布

四种情况下基桩0～65.5 m深度范围内的界面抗剪强度的计算结果见图4。

图4 界面抗剪强度随埋深的变化曲线

界面摩擦强度取决于桩土界面的摩擦特性，其仅受内摩擦角的影响，各种土的界面摩擦强度均随深度线性递增呈三角形分布，内摩擦角越大，递增速率也越大。

由土体抗剪强度和界面抗剪强度的相互耦合可以得出极限侧阻力随深度的变化曲线(见图5)。无粘性土的土体抗剪强度和界面抗剪强度均随深度线性递增，极限侧阻力也随深度线性递增呈三角形分布；受计算深度限制，Ⅰ类粘性土和Ⅱ类粘性土在计算深度内的界面抗剪强度小于土体抗剪强度，极限侧阻力在图5内由界面抗剪强度决定而显示为三角形分布，实际上4.3节已经说明了该两类粘性土的土体抗剪强度在深层土体范围内的递增速率不断减小，在某一深度以下土体抗剪强度将小于界面抗剪强度，极限侧阻力将由土体抗剪强度决定，为了说明这一分布特征，将桩周淤泥质粘土④和粘土⑤1a的计算深度延伸至88.0 m，并假定它们的界面摩擦角与内摩擦角相等，即假定桩侧表面与土体不发生相对滑动，在这一假定条件下计算出的淤泥质粘土④和粘土⑤1a的极限侧阻力随深度的分布绘制成图6，从图6可以看到，Ⅰ类粘性土的极限侧阻力随深度将呈上部线性递增三角形+下部非线性递增近似梯形分布，Ⅱ类粘性土则随深度呈上部线性递增三角形+下部非线性递增近似矩形分布；Ⅲ类粘性土的极限侧阻力随埋深在浅层土体范围内由界面抗剪强度决定线性递增呈三角形分布，在深层土体范围内则受土体抗剪强度决定而非线性递减直至为零，并随深度增加一直为零。

图5 极限侧阻力随埋深的变化曲线

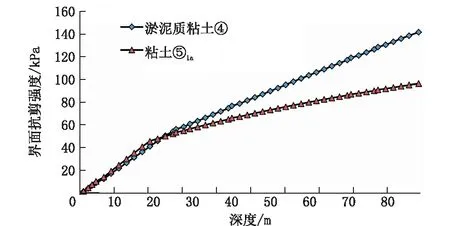
图6 极限侧阻力随埋深的变化曲线 (内摩擦角等于界面摩擦角)Fig.6 Curves of ultimate shaft friction versus buried depth(The interface friction angle is equal to the internal friction angle)

5 结论

(1)根据文献[9]的相关分析结果得出沿桩土界面方向的土体抗剪强度的计算模型，结合桩土界面的界面抗剪强度计算模型，得出受土体抗剪强度和界面抗剪强度相互耦合作用的极限侧阻力计算模型，运用该计算模型对算例的计算结果与测试结果接近，具有较好的工程应用性。

(2)界面抗剪强度和土体抗剪强度分别反映了桩土界面的摩擦特性和桩周土体的应力状态，两种强度的相互耦合作用影响了侧阻力的发挥，为充分调动土体抗剪强度进而充分发挥侧阻力，采取后注浆或减小泥皮厚度等措施提高界面抗剪强度是十分有必要的。

(3)粘聚力和内摩擦角对土体抗剪强度的作用不同，粘聚力将赋予浅层土体的土体抗剪强度一个初始值，而内摩擦角则会因其与侧压力系数之间的不同关系而使深层土体抗剪强度表现出随深度不同的变化特点。在同样深度处，浅层粘性土的土体抗剪强度要大于无粘性土，深层粘性土的土体抗剪强度则小于无粘性土。

(4)无粘性土与Ⅰ类粘性土的极限侧阻力随深度增加不断增大，分别呈三角形和上部三角形+下部近似梯形的分布；Ⅱ类粘性土和Ⅲ类粘性土则存在一个临界深度，Ⅱ类粘性土的极限侧阻力在临界深度以上呈三角形分布，在临界深度以下随深度增加其极限侧阻力增加不明显而趋于一个稳定值；Ⅲ类粘性土的极限侧阻力在临界深度以上呈三角形分布，在临界深度以下则不断减小直至为零。