基于LVQ网络优化的雷达目标识别算法

， ，

(海军航空大学信息融合研究所， 山东烟台 264001)

0 引 言

雷达目标一维距离像识别是利用高分辨雷达的目标回波所提供的相关信息，对目标的类别属性等进行相应的判决。一维距离像能够反映目标的几何形状和结构信息，相较于低分辨率雷达可以提供更多所需的特征信息，而且易获取和处理。因此利用雷达目标的一维距离像进行目标识别[1-2]成为热门的方法。已有研究提出了将子空间法、最优聚类中心法、BP神经网络[3-5]等应用于雷达目标一维距离像识别，并取得了不错的效果。

神经网络作为一种性能优良的分类器，在近些年得到了飞快的发展。其最大的特点就是具有很强的自适应能力，不但能够自适应地学习，还能自适应地调整网络规模的大小。LVQ神经网络拥有很强的分类识别能力，得到了广泛的应用[6]。本文将其作为分类识别器应用到雷达目标的一维距离像识别中，取得了不错的效果。LVQ网络算法存在对输出层和竞争层初始连接权值敏感的问题，针对这个本文采用PSO算法进行优化改进，提出PSO-LVQ雷达目标一维距离像识别算法。经实验验证，该方法明显提高了识别效果。

1 LVQ神经网络模型分析

LVQ神经网络是一种用于训练竞争层的有监督的网络，其算法源自于Kohonen竞争算法[7]。图1为LVQ神经网络结构示意图[8]。LVQ神经网络有3层神经元：输入层、竞争层和输出层。设每个距离像为向量Xi，输入层的每个输入模式均为一个距离像。该网络输入层和竞争层之间采用全连接的方式，其连接权值在进行网络训练的时候会发生改变，网络训练就是竞争层对输入的向量依据距离最近准则进行学习分类。输出层的每个神经元对应于一种雷达目标类别。

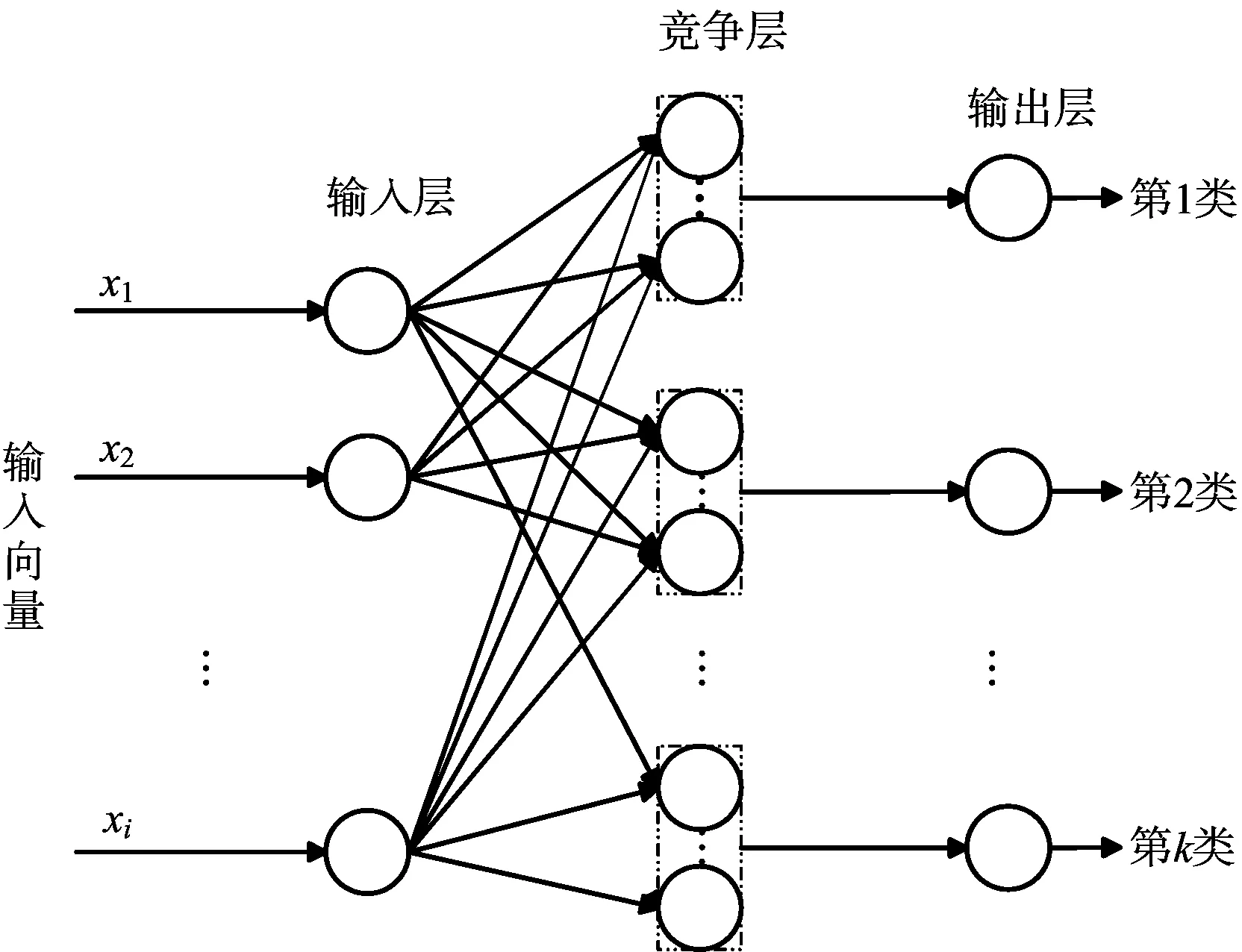
图1 LVQ神经网络模型

在利用LVQ神经网络进行雷达目标一维距离像识别的时候也发现一些问题。通常“获胜”的神经元通过计算最小距离来确定，只利用“获胜”神经元的信息导致输入样本和竞争层之间的信息资源利用不充分。容易发现当初始权值偏差过大的时候，计算误差就会很大，会影响LVQ网络的收敛速度和分类识别的效果。

2 PSO-LVQ雷达目标一维距离像识别算法

针对上述提及的LVQ网络对输出层和竞争层初始连接权值敏感的问题，本文提出了PSO-LVQ雷达目标一维距离像识别算法。

图2为基于PSO-LVQ的雷达目标一维距离像识别流程图，实验整个过程主要分为数据预处理、生成LVQ网络、PSO算法优化网络权值、建立模板库及测试识别判断几个部分。

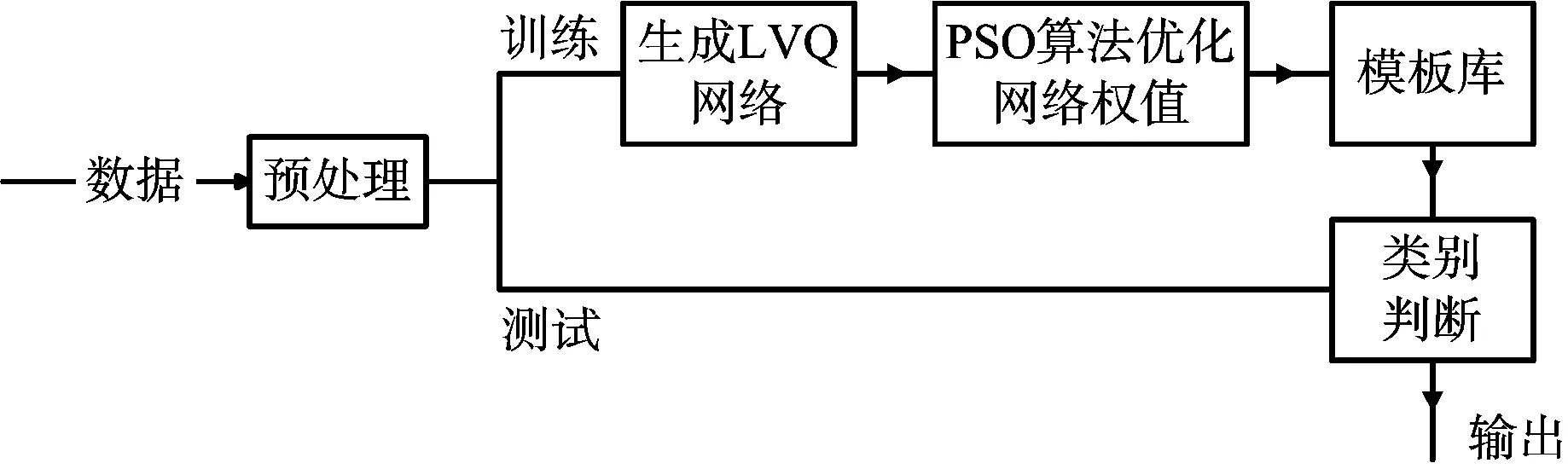
图2 基于PSO-LVQ的雷达目标一维距离像识别流程图

2.1 数据预处理

一维距离像存在着方位敏感性和幅度敏感性，它们是一维距离像识别的关键问题之一。为了有效地识别目标，必须进行数据的预处理。傅里叶变换(FFT)[9]法在频域具有平移不变性，对目标的一维距离像作傅里叶变换，在时域里的平移对频域没有产生影响，这样能够克服雷达目标一维距离像的平移敏感性。对距离像幅度谱进行归一化解决幅度敏感性[10]。

2.2 PSO算法优化网络权值

粒子群优化算法[11]是由Kennedy和Eberhart等提出的模拟鸟的群体智能行为的一种优化算法。粒子群算法中，一个粒子代表一只鸟，每个粒子用其自身的位置和速度来表示，并依据自身的初定方向、自己的经验最优方向和周围粒子的经验最优方向来更新其位置和速度。通过定义适应度函数来评价每个粒子的表现。

本文采用粒子群算法对LVQ神经网络初始权值进行优化选择。将粒子群的粒子编码直接赋值给LVQ神经网络的权值和阈值矩阵，然后通过LVQ神经网络预测得到预测值，与训练数据的实际值进行比较，以预测失误率和为目标函数，得到每个粒子的适应度。图3为PSO-LVQ神经网络权值优化算法的流程图。

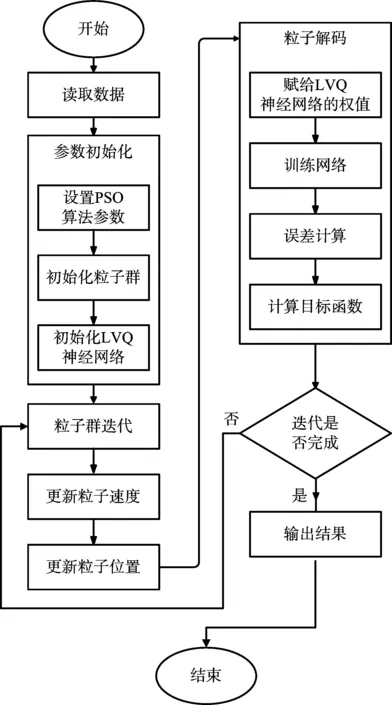
图3 PSO-LVQ神经网络权值优化算法流程图

2.2.1 参数初始化

设置PSO算法的参数c1,c2,r1和r2，初始化粒子群，即定义种群规模、迭代次数等参数，初始化粒子的速度和位置。

创建LVQ神经网络，每个目标选取一定数量的样本作为网络训练的输入向量，随机产生n×m维的矩阵(n为LVQ网络的隐含层神经元数，m为一维距离像的维度)作为网络的初始权值。隐含层神经元数会影响网络的效果，过少会影响识别精度，过多则会影响训练的速度，依据实际的实验确定其数目。输出层每个神经元对应于一种雷达目标类别。种群迭代更新：

粒子的速度计算如式(1)所示：

vij(t+1)=vij(t)+c1r1[yij(t)-xij(t)]+

(1)

粒子的位置计算如式(2)所示：

xij(t+1)=xij(t)+vij(t+1)

(2)

2.2.2 粒子解码

粒子解码就是将粒子编码直接赋值给LVQ神经网络的权值,并通过LVQ神经网络预测得到预测值,与实际值比较后,以预测错误率和为目标函数, 得到每个粒子的适应度。

设每个距离像为向量Xi，输入层的每个输入模式均为一个距离像。假定K类目标共有M个距离像，则输入为X=(x1,x2,…,xM)，则输入神经元个数也为M，按照如下步骤进行训练：

第一步 初始化输入层和竞争层之间的连接权值ωij和学习速率η(0)，η>0，其中i=1,2,…,P，P为竞争层神经元数目，j=1,2,…,M；

第二步 将一维距离像作为输入送入网络，计算输入向量与竞争层神经元之间的欧式距离：

(3)

第三步 建立最小欧式距离标准，与输入向量欧式距离最小的神经元di获胜，与之连接的输出层神经元的标签记为Cx，与输入向量对应的别类标签为Ci；

第四步 判断是否正确分类，依据以下规则调整权值向量：

当Cx=Ci时，则

wij_new=wij_old+η(x-wij_old)

(4)

当Cx≠Ci时，则

wij_new=wij_old-η(x-wij_old)

(5)

第五步 调整学习速率：

(6)

第六步 判断迭代次数n是否超过N，若超出则迭代结束，否则转到第二步。

这种训练方法的优势在于不需要对输入向量进行归一化和正交化，只需计算输入向量和竞争层神经元之间的距离。

PSO-LVQ优化算法的具体实现步骤如下：

1) 创建LVQ网络；

2) 初始化粒子群，定义种群规模、迭代次数等参数，初始化粒子的速度和位置；

3) 迭代寻优，调整粒子的速度和位置；

4) 计算适应度值，更新个体极值和群体极值；

5) 重复3)、4)两步，直到迭代完成；

6) 将最优值赋值给LVQ神经网络，输入样本进行训练；

7) 输出结果。

3 实验仿真

3.1 实验条件

实验采用的实测数据是国内某研究所的ISAR实验飞机数据，实验飞机有3种，分别为安-26、桨状和雅克-42。雷达为逆合成孔径C波段雷达，中心频率约为5.5 GHz，波长约为0.05 m，信号带宽为400 MHz，距离分辨率为0.375 m，采样点数为256。每种飞机记录了7段数据，每段数据含26 000个宽、窄带信号(间隔2.5 ms)。宽带信号为全去斜后的正交双通道信号(其FFT即为一维距离像)，每段数据含260个宽带正交双通道信号。实验数据为3种飞机各取一段的260幅距离像。对数据进行如下处理：

第一步 归一化，将每一幅图像用其总能量归一化；

第二步 距离对准，利用Fourier变换的平移不变性，将一维距离像作Fourier变换即可对齐。

每种目标选取160个样本组成训练集，剩余100个样本组成测试集。设置隐含层神经元数为20个，粒子群种群的规模为50，迭代次数为50次。

3.2 结果分析

如表1所示为LVQ算法和PSO-LVQ算法的分类准确率。

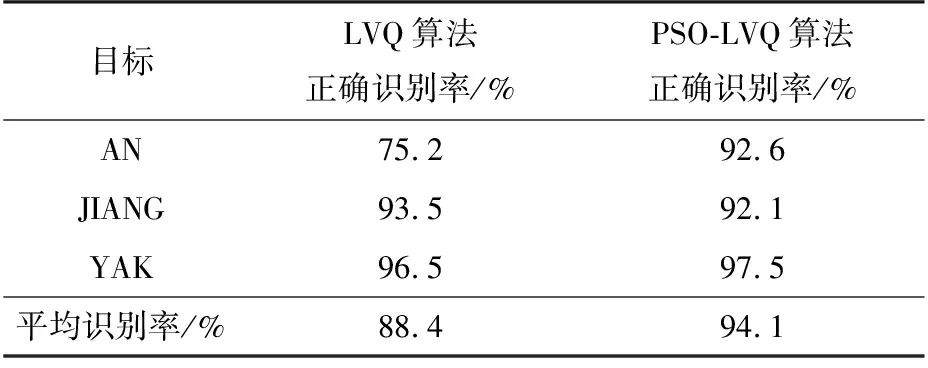
表1 LVQ, PSO-LVQ算法分类准确率比较

通过表1能够直观地看到PSO-LVQ算法的分类准确率要比LVQ的好很多，平均准确率可以达到94.1%，这说明经过PSO算法对LVQ神经网络的权值进行优化之后，在一定程度上克服了LVQ神经网络对于初始权值的敏感性，使网络的分类效果更好。实验证明了该算法的正确性。

图4为PSO-LVQ算法训练样本集ROC曲线，ROC曲线下面积越接近1说明分类的效果越好。很明显能看出，3类目标ROC曲线下面积都将近1，说明在用粒子群算法优化LVQ神经网络的权值之后，分类器的分类效果良好。

图4 PSO-LVQ算法训练样本集ROC曲线

4 结束语

本文详细介绍了LVQ神经网络模型，利用其稳定的分类识别能力来进行雷达目标一维距离像的识别，取得一定的识别效果。在此基础上，针对LVQ神经网络对初始连接权值敏感性的问题，采用粒子群优化算法对其进行优化，从而提高网络的性能和稳定性。经过实验表明，由粒子群权值优化后的LVQ神经网络，在识别性能上有了进一步的提升，从而验证了PSO优化算法在一定程度上能克服LVQ神经网络对于初始权值的敏感性，增强网络的性能。需要指出的是，没有考虑数据的不同信噪比对目标分类识别率的影响，这是接下来要继续开展工作的地方。