基于压缩感知的农情监测节点稀疏采样决策方法

赵刚，饶元，朱军，李绍稳

(安徽农业大学信息与计算机学院，安徽 合肥 230036)

农业物联网系统已经成为农业大数据最重要的数据源之一[1]。通过将具有感知、通信和计算能力的微型传感器部署应用于农业生产管理中，全面、准确、高效地监测SPAC(土壤-植物-大气连续体)系统，能够有效推进“互联网+”现代农业行动，为精准农业的实现提供重要支撑[2,3]。

对基于物联网技术自动获取的数据进行质量控制是开展高价值农业生产分析以及基础科研数据应用的重要前提。农情监测网络通常部署在野外环境，持续供电困难，有限的通信带宽也给数据可靠交付带来了极大挑战。实现节点长期稳定运行与高效数据获取一直是农业无线传感器网络部署应用亟待突破的关键瓶颈问题。为提高数据采集效率、延长网络生命周期，研究者们分别从路由算法、数据压缩与融合等方面开展研究，试图减少节点所采集数据的冗余度、降低网络中的数据传输量[4]。

压缩感知CS(Compressive Sensing)技术的出现为解决上述问题提供了新思路。传感器节点能够以较低的速率在采样的同时对信号进行适当压缩，Sink端通过求解一个优化问题就可以高概率精确重构原信号，有效减少传感节点的数据获取能耗[5]。测量矩阵、信号稀疏表示和重构算法等三要素是决定基于压缩感知的数据采集质量关键性因素[6,7]。稀疏基矩阵能够对采样信号进行稀疏化，测量矩阵用来表示采样策略，重构算法的选择对信号恢复质量和代价有着决定性作用。根据参与数据采集的节点规模，常用的压缩感知方法可分为多节点协同调度采样[7,8]和单节点调度采样[5,9～11]。当前农情传感器成本较高，大规模应用部署较为困难。实际农业生产环境中，通常采用选取少量代表性站点进行监测，故单节点的稀疏采样方法研究更为实用。然而，针对不同的数据对象，压缩感知三要素的具体实现形式与算法往往存在较大的差异。

为此，笔者全面分析了基于压缩感知的单节点稀疏采样与重构方法，设计并使用Python语言开发了基于压缩感知的农情监测节点稀疏采样决策系统，以便于实际农情数据采集中，快速有效开展测量矩阵、信号稀疏表示和重构算法等三要素的组合应用效果评估，为实现高效率、高质量农情数据的获取提供支撑。

1 基于压缩感知的单节点数据稀疏采样与重构

压缩感知利用被采集数据的稀疏特征和原始数据的低秩特性，将物理世界的传感数据进行稀疏化表示，在小于Nyquist采样率的条件下, 获取信号的少量离散样本，然后通过非线性重建算法恢复信号。记某传感器节点一定时间内采集的物理量时序为X=[x1,x2,…,xN]T，假设向量ψi是RN空间中的N维列向量，组成基矩阵Ψ= [ψ1,ψ2, ….,ψN]，则RN空间的任意信号X都可表示为：

(1)

压缩感知理论指出，在稀疏条件下，用一个与Ψ满足有限等距性(Restricted Isometry Principle, RIP)约束的观测矩阵Φ∈RM×NM≼N对X进行线性亚采样得到观测值Y，可以通过Y求解优化问题精确的重构出X[5,10]，该理论可表达为：

s.t.Y=ΦΨα

(2)

基于压缩感知的节点稀疏采样与重构研究需要面对3个方面的问题[7～10]：

Ⅰ、对采样策略设计M×N测量矩阵Φ，使M尽量小以减少采样次数。

Ⅱ、稀疏矩阵的构建，针对X的特征，为稀疏化X而设计稀疏基Ψ。

Ⅲ、对已知的测量信号Y和矩阵Φ、Ψ，根据重构算法Ω，确定α，重建原始信号X=Ψα。

图1 单节点采样测量矩阵

对于问题Ⅰ，传统的高斯随机测量矩阵、随机贝努利矩阵[6,10]等并不适用。传感器节点在同一时刻只能采样一次，故单节点采样调度的测量矩阵每列最多一个“1”，每行有且仅有一个“1”，其余元素全为“0”，其基本结构如图1所示，该矩阵表示对一个长度为N的离散信号X进行M次采样。矩阵元素(m,n)=1表示节点的m次采样在n时刻发生，(m,n)=0代表非采样点。该矩阵包含“1”的列可随机分布或等间隔均匀分布，分别对应随机采样和均匀采样。随机采样中，节点随机选择M个时刻采样。周期性采样策略是指节点按照N/M等间隔采样M次。M值决定了节点执行采样的总次数，对于节点能耗与数据恢复效果有着关键作用。

定义采样率p=M/N。采样率越低，节能效果越好，但可能会导致较大的数据恢复误差。故设计采样调度策略时要根据对恢复数据的精度需求来对二者进行权衡。为此，长期的数据采集过程中，可结合数据的变化特征动态调节采样率。通过降低线性变化数据段的采样率，提高非线性变化数据段的采样率，以平衡采样率和数据恢复间存在的矛盾。具体地，设基准采样率pbase，将节点数据采集过程分解为多个子采样段，各段采样率SRi动态调整方法如下[5,10]：

(3)

(4)

式(3)通过分析历史同期数据的变化特征来确定当前时间段的采样率[5]，式(4)根据前期相邻时间段内数据特征预测其未来变化趋势，动态调节点的采样率[10]。

对于问题Ⅱ，选择的稀疏矩阵Ψ要能够很好的稀疏化目标信号X。正交变换基容易实现且重建准确度高。最常用于一维信号稀疏化表示的正交基有离散余弦变换DCT (Discrete Cosine Transform)、离散小波变换DWT (Discrete Wavelet Transform)和差分矩阵等[7,9,11～13]。其中，差分矩阵的逆具有如图2所示的结构，通常元素ζ>0以确保MD可逆。

图2 差分矩阵结构图

对于问题Ⅲ，第1类是基于l0范数的贪婪迭代算法，其通过迭代的方式寻找稀疏向量的支撑集，并使用受限支撑最小二乘估计来重构信号[14～16]。这类算法计算复杂度较低，但需要较高的采样率，重建精度低。主要包括匹配追踪算法MP (Matching Pursuit)、正交匹配追踪算法OMP (Orthogonal Matching Pursuit)、CoSaMP算法(Compressive Sampling Matching Pursuit)、子空间追踪算法SP (Subspace Pursuit)以及SL0算法(Smooth Norm)等。第2类是基于l1范数的最小化松弛算法，将求解最小l0范数转化为求解最小l1范数，利用凸优化方法求解原问题[14～16]。这类方法重建精度较高，但需要较低的采样率，计算复杂度较高。特别地，SL0、基追踪算法BP和子空间追踪算法SP在一维数据重构方面恢复精度较高[5,9,10]。

2 决策系统功能设计与实现

2.1 系统功能设计

系统由采样率调节、核心功能和辅助功能等组成，采用Python3.6语言开发。如图3所示，采样调节模块实现了固定/动态采样方式，其中固定采样即直接使用预先设定的基准采样率，动态采样则是基于历史同期数据特征的自适应调节采样率、基于数据趋势预测的自适应调节采样率，分别对应于式(3)和式(4)的2种采样率自适应更新方法。核心模块包括压缩感知三要素：测量矩阵、稀疏基和重构算法的实现。辅助模块有数据导入/导出、图形展示和算法评价等模块，主要实现数据导入、算法评价结果输出和数据图形化展示等功能。各模块独立封装，使用时直接传参调用，可扩展性强。

2.2 实现技术及效果

2.2.1采样率调节实现

图4所示的是采样率调节组成及实现方式。定义采样率调节 samplerate_adjust_func类，包含固定采样函数fixed_sampling_rate(pbase)、历史同期数据特征自适应采样函数hist_sampling_rate(pbase,data)和基于数据趋势预测自适应采样函数pre_sampling_rate(pbase, data)。其中，参数pbase为基准采样率，data是输入的历史数据。以上函数调用NumPy、Math和Scipy工具包，返回值均为采样率srate。

固定采样函数fixed_sampling_rate(pbase)返回基准采样率。历史同期数据特征自适应采样函数hist_sampling_rate(pbase,data)调用Scipy库函数scipy.stats.pearsonr()求取所输入数据的皮尔逊系数，再平方后获得决定系数R2，随后采用历史平均决定系数与R2的差乘以调节基数获得同期采样率变化值，最后加上基准采样率得到实际的采样率。基于数据趋势预测自适应采样函数pre_sampling_rate(pbase, data)调用库函数scipy.stats.pearsonr()求取最近2个数据段的决定系数，根据决定系数之差预测下一段数据的采样率。

图3 基于压缩感知的农情监测节点稀疏采样决策系统功能架构

图4 采样率调节模块组成及实现方式

2.2.2核心功能实现

图5所示的是测量矩阵、稀疏基和重构算法等核心模块的组成及实现方式。

1)测量矩阵。定义measure_matric_func类，包含高斯测量矩阵生成函数gauss_meas_matric(srate, len) 、周期测量矩阵生成函数period_meas_matric(srate, len)和随机测量矩阵生成函数rand_meas_matric(srate, len)。其中，参数srate是采样率，len是待采样信号长度。以上函数调用NumPy和Random工具包，返回值均为(srate*len)×len的测量矩阵Phi。

高斯测量矩阵生成函数gauss_masure_matric(srate, len)直接调用numpy.random.randn(srate*len,len)构建。周期测量矩阵生成函数period_masure_matric(srate, len)先调用numpy.zeros()初始化测量矩阵，接着对矩阵从左上角首元素起每隔⎣N/M」行、⎣N/M」列的元素赋值1，再使用numpy.insert()将矩阵尾部连续的零列插入矩阵内。随机测量矩阵生成函数rand_masure_matric(srate, len)先调用numpy.zeros()初始化测量矩阵，再采用random.sample()生成随机数集合，接着用Python内建排序函数sort()排序，最后以随机数集合作为列号将初始化矩阵中的相应列元素赋值为1构造随机测量矩阵。

图5 核心模块组成及实现方式

2)稀疏基。定义sparse_matric_func类，实现差分矩阵diff_sparse_matric(len)、离散余弦变换基dct_sparse_matric(len)和离散小波基dwt_sparse_matric(len)等3种稀疏基构造函数。其中，参数len是待采样信号长度。以上函数调用NumPy、Math工具包和PyWavelets小波工具箱，返回值是大小为len×len的稀疏矩阵。

差分矩阵diff_sparse_matric(len)调用numpy.eye()构造差分矩阵框架，接着替换矩阵最后一个元素，再使用numpy.linalg.inv()求取矩阵的逆得到差分稀疏矩阵。离散余弦变换基dct_sparse_matric(len)调用零矩阵生成函数numpy.zeros()、余弦求值函数numpy.cos()、矩阵点积函数numpy.dot()、矩阵均值函数numpy.mean()和矩阵范式求解函数numpy.linalg.norm()。离散小波基dwt_sparse_matric(len)采用PyWavelets工具包中的Wavelet函数对’haar’小波基进行高通和低通滤波得到该小波的高频系数和低频系数部分，再调用numpy.flip()函数对分解的高频系数和低频系数进行列向量转置翻转、numpy.roll()进行矩阵移位、numpy.hstack()进行融合等处理，最后构造出离散小波基矩阵。

3)重构算法。定义rec_ algorithm_func类，实现SL0重构算法rec_ algorithm_SL0(y,A)、基追踪重构算法rec_ algorithm_BP(y,A)、子空间追踪算法rec_ algorithm_SP(y,A)等3种重构算法。其中，参数y为观测值，A为感知矩阵(测量矩阵与稀疏基之和)。以上函数共调用NumPy、SciPy和Math工具包，返回值为重构的数据。

SL0重构算法rec_ algorithm_SL0(y,A)调用求逆函数numpy.linalg.pinv()，根据平滑l0范式的重构算法原理构建。基追踪重构算法rec_ algorithm_BP(y,A)利用numpy.ones()和numpy.hstack()处理线性规划模型参数，然后采用线性规划模型函数scipy.optimize.linprog()优化求解该参数，以重构数据。子空间追踪算法rec_ algorithm_SP(y,A)调用math.floor()函数和NumPy工具包中的求逆函数numpy.linalg.inv()、取绝对值函数numpy.fabs()和范式求解函数numpy.linalg.norm()等。

2.2.3辅助功能实现

图6所示的是辅助模块组成及实现方式。

1)数据导入导出。定义data_in_out类，包含数据导入函数data_import()和数据导出函数data_output()。调用Pandas工具包和GUI库Tkinter。数据导入函数data_import()调用tkinter.askopenfilename()函数弹出文件选择框，返回用户所选择文件的完整路径，再由pandas.datetime.strptime()指定表头和读取格式，采用pandas.read_excel()/pandas.read_csv()接收文件路径及读取格式后完成Excel/CSV文件数据的读入。数据导出函数data_output()调用tkinter.asksaveasfilename()函数和Python内建函数open()。使用tkinter.asksaveasfilename()函数创建目标文件，再由内建函数open()以’w’模式将缓存区数据写入到文件。

图6 辅助模块组成及实现方式

2)算法评价与图形化展示。定义eval_graph类，实现算法评价指标和数据图形化展示等功能，调用NumPy库和Matplotlib绘图库。算法评价指标包括信噪比函数SNR()和均方根误差RMSE()函数。函数Plot_curve()调用Matplotlib绘图库的Canvas控件及NavigationToolbar2TkAgg组件，实现数据曲线的展示、缩放、拖拽和图片保存等功能。

2.2.4系统界面效果

基于以上实现技术，采用Python3.6实现各功能模块并有机整合。决策系统界面如图7所示，主要由导入数据、数据源选择、分段数、采样方式、测量矩阵、稀疏基、重构算法、采样重构和导出结果等部分组成，各部分按照操作步骤编号。系统的【数据显示】模块提供原始数据与重构数据展示、重构数据相对于原始数据的偏差度分析功能，支持曲线图的缩放、拖拽和保存，便于开展压缩感知三要素的遴选。

3 系统应用与分析

试验数据来自安徽农业大学农萃园，自2016年3月13日起部署以色列植物生长监测仪PM11z、基于Arduino Mega2560研发的数据采集节点不间断收集园区园艺花卉育苗日光温室大棚内外的环境信息、土壤温湿度(SWR-100W型土壤温湿度传感器)、花卉植株茎流(TDP-10型植物茎流计)等本体信息，采样间隔为15min。笔者取2017年9月1日至30日共30d时间段内植株茎流和土壤湿度数据(见图8)。其中，植株茎流、土壤湿度均呈周期性变化，植株茎流变化周期为24h，土壤湿度变化周期与灌溉间隔时长有关。

为全面评估采样率调节方法、压缩感知三要素的功用，通过设置数据分段、基准采样率，选择不同的采样率调节方法、测量矩阵、稀疏基和重构算法组合，全面评估不同组合条件下的数据稀疏采样及其重构效果。试验过程中，设置基准采样率为10%、30%。采用分段数1、3、6、10、15、30和60，分别对应采样时段长度为30、10、5、3、2、1、0.5d。试验过程中发现采用差分矩阵、重构算法SL0较其他重构算法消耗的重构时间更短，但具有更好的恢复效果，后续分析仅提供稀疏基、重构算法分别为差分矩阵、SL0算法时的重构效果。选取信噪比SNR(Signal-Noise Ratio)作为数据重构精度的评价指标。

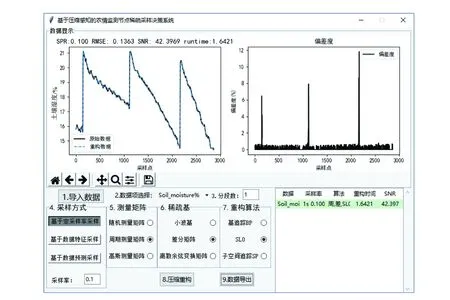
图7 稀疏采样决策系统界面

图8 植株茎流与土壤湿度数据

图9表示的是植株茎流数据不同数据稀疏采样下的重构效果。为排除动态采样调节的干扰，选取10%、30%两种定采样率评估不同测量矩阵下的重构效果，结果如图9(a)所示。随着采样率的增加数据重构效果明显变好，周期测量矩阵的重构效果显著优于随机和高斯测量矩阵，且过细的分段采样对于重构效果的提升有限，甚至有负面影响(分60段时)。采样率从10%提升到30%时，更多的原始数据参与重构提升了数据重构效果。若用于重构的数据量过少，原始数据的稀疏性及RIP条件的充要条件受到负面影响，导致1d以内的数据为重构单元时恢复效果变差。

为评估不同采样率调节方式对重构效果的影响，分析同一测量矩阵在定采样率、基于历史同期数据特征和基于数据趋势预测的自适应采样率调节方式下的数据重构效果。图9(b)所示是采用周期测量矩阵时3种采样率调节方式的重构效果。特别地，随机和高斯测量矩阵下的重构效果与图9(b)类似。故可得出，不同采样率调节方式对重构结果的影响无明显差异。

图9 不同数据稀疏采样下植株茎流数据重构效果

因此，压缩感知方法应用于植株茎流数据采集时，宜选取固定采样率、周期测量矩阵进行稀疏采样；以1d以上的数据序列为单位进行重构较为合适；高频率采样的数据有着更好的重构效果，如采样率从10%上升到30%，信噪比提升30%。

图10 定采样与不同测量矩阵下土壤湿度重构效果 图11 定采样率与周期测量矩阵下各分段的重构时间

土壤湿度数据在定采样与不同测量矩阵下重构效果如图10所示。数据重构效果随着分段数、采样率的增加而上升。此外，通过分析不同采样率调节方式的重构效果，可得3种采样调节方式未对重构结果造成明显的影响。因此，压缩感知方法应用于土壤湿度采集时，宜选取固定采样率、周期测量矩阵进行稀疏采样；数据序列重构单位越小越好；高频率采样的数据可获得更好的重构效果。

综合以上分析可知，采用压缩感知方法采集植物茎流、土壤湿度数据时，宜采用固定采样率，分别选取周期测量矩阵、差分矩阵、SL0算法为测量矩阵、稀疏基和重构算法，数据重构单元因数据对象不同而有所差异。值得注意的是，重构数据不可避免地与原始数据存在偏差，且偏差对实际应用的影响与应用场景密切相关，具体偏差大小可通过改变采样率进行调节。采用10%采样率时，重构数据的取值、变化趋势等与原始数据符合度较高，可满足田间生产管理需求。

具体应用中，重构时长也是数据重构单元选取的重要因素之一。图11为植株茎流和土壤湿度2组数据在不同分段数、定采样率和周期性测量矩阵下的重构时间对比，运行环境为Intel i5处理器、4GB内存、Windows 7操作系统。可以看出，重构时长均是在分段数达到3(10d数据)后显著下降，此后逐步趋于稳定。故针对植株茎流、土壤湿度数据的压缩感知采集，可每2～10d进行一次稀疏采样数据的重构。

4 结语

探索农情数据的高效采集是农业物联网研究中一项非常有意义的工作。笔者研发了基于压缩感知的农情监测节点稀疏采样决策系统，实现了采样率调节、测量矩阵、稀疏基和重构算法的多组合调用。通过对30d连续监测、采样间隔为15min的花卉植株的茎流、土壤湿度数据压缩感知分析，验证了该系统能够为基于压缩感知理论的农情数据稀疏采样决策提供有效支撑。后续将深入开展基于压缩感知的非周期性变化、视频图像等复杂农情数据的稀疏采样方法研究，为全面提升农情数据的获取质量与效率提供支撑。