基于EGM2008重力场模型的GPS高程转换在复杂地形中的应用研究

张荣斗， 郭火元， 张 进

(四川中水成勘院测绘工程有限公司， 四川 成都 610072)

0 前 言

利用GNSS测量的方法代替传统的几何水准测量，是目前GNSS技术在高程测量应用的一个热点，其实质是求解高程异常值ζ。通常求解高程异常的方法可以分为两大类，即：数值逼近法和重力场模型法。

重力场模型法是指某点的高程异常是通过重力测量或者通过地球重力场模型计算得到。重力场模型法求解高程异常是由于缺乏重力数据以及重力场模型绝对精度不高、分辨率低等，在实际工程中，难以得到广泛应用。

EGM2008是近年来NGA释放的全球超高阶地球重力场模型，该模型的阶次完全至2 190阶次，与其他模型(EGM96、GGM03C等)相比精度有较大提高，是迄今为止分辨率和精度最高以及阶次最多的全球重力场模型。本文拟采用“移除-恢复”的思想，分析和研究利用EGM2008地球重力场模型、数值逼近进行复杂地形条件下的GNSS高程转换的方法。

2 EGM2008重力场模型的求高程异常方法及精度分析

2.1 EGM2008地球重力场模型求高程异常

2008年4月，NGA(美国国家地理空间情报局)发布了最新的全球重力场模型，命名为EGM2008。该模型在计算时综合了最新的GRACE卫星跟踪数据、地面重力数据、卫星测高数据，最大阶数展开到2 190阶，模型的空间分辨率为5′(约9 km)，是目前分辨率和精度最高的重力场模型。EGM2008提供了包括2 190阶次的全球重力场模型，全球5′×5′格网重力异常，全球5′×5′、2.5′×2.5′格网大地水准面，全球5′×5′格网垂线偏差的最终成果。

EGM2008模型解算大地水准面的原理仍与EGM96模型类似，是将一个逼近地球质体外部引力位在无穷远处收敛到零值的调和函数展开成在理论上收敛的整阶次球谐函数的2 190阶次的级数。由完全展开到2 190阶次的球谐函数求得扰动位T。

再根据Bruns公式可求得地面上任意一点的高程异常：

(1)

2.2 精度分析

由于EGM2008地球重力场模型扩展到2 190阶次的截断误差已趋于0，所以它的模型误差仅包含由位系数等误差传播引起的误差，全球5′×5′格网大地水准面的估算精度显示：误差最小为3.045 cm，最大为102.194 cm，均方根为11.137 cm。

ICGEM为了检测EGM2008模型的精度，并与经典的EGM96(360阶次)、EIGEN-CG03C(360阶次)模型做比较，采用国家区域范围的GNSS水准进行检测，将GNSS水准点的正高与地球重力场导出的正高比较，二者的差值在一定程度上反映了由重力卫星数据导出的各类地球重力场模型的实际精度。表1为在相应地区这一差值的均方根，表中括号内值为GNSS水准点个数。结果显示，新重力场模型EGM2008精度较经典的EGM96，ElGEN-CG03C模型提高很多。

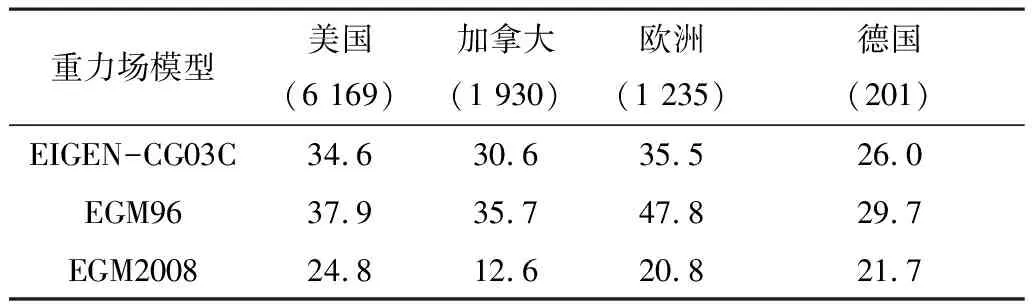
表1 GNSS水准点正高与重力场模型相应点正高差值的均方根 cm

章传银、郭春喜、陈俊勇等利用全国GNSS A、B级网的GNSS水准数据，及华北、华南、华中、华东等地区GNSS水准资料对EGM2008重力场模型在中国大陆的适用性进行研究，结果表明：EGM2008重力场模型高程异常精度在华北地区达到9 cm，华东华中地区12 cm，西部地区精度稍差为24 cm。

3 “移除-恢复”原理

根据物理大地测量学的理论，高程异常可表示为：

ζ=ζGM+ζΔG+ζT

(2)

式中，ζGM是由重力场模型所计算的长波项；ζΔG表示中波部分，可以通过求解重力异常的边值问题得到；ζT表示短波部分，通过求解地形改正得到。由于没有数字高程模型数据，所以在本文中没有单独考虑地形改正部分ζT了，而在本文中是把ζΔG与ζT部分合在一起用数学模型逼近的方法来表征，表示为δζ，所以式(2)变换为：

ζ=ζGM+δζ

(3)

“移除-恢复”思想：通过n个已知GNSS水准联测点可求得其高程异常ζn，用地球重力场模型EGM2008式(1)可计算出已知GNSS水准联测点的ζGM，然后将ζGM移除可得到残差大地水准面δζi=ζ-ζGM，残差大地水准面是由于模型误差、公式误差或系统误差而引起的，具有一定的随机性，可通过数学函数来拟合。实际工程中大多采用二次曲面函数来拟合，拟合函数如下：

δζ=a0+a1x+a2y+a3x2+a4y2+a5xy

(4)

通过已知GNSS水准联测点可以求得该拟合函数模型，然后在未知点上用式(1)和式(4)求和 ，最后再用式(3)求该点的高程异常。

4 实例分析

本文结合实际工程，选择两个区域实测的GNSS水准数据，对基于EGM2008地球重力场模型采用“移除-恢复”法求解高程异常解算精度，按下述方案分别进行统计分析。

方案1：不加入EGM2008模型，选测区内若干个均匀分布的点作为已知高程异常点，直接采用二次曲面函数拟合法。

方案2：加入EGM2008模型，采用“移除-恢复”方法进行高程转换。将两种方案所解算的高程异常与实测高程异常之差进行统计，按公式(5)计算各自的内符合精度和外符合精度。

(5)

式中，v表示已知点或检验点的拟合高程异常与实测高程异常值的差值；n表示参与精度评定的点的个数。

4.1 数据计算

区域一位于川西地区某县，图1为该县组合城市地形测绘GNSS控制网，共52个点，其中12个D级GNSS点、40个E级GNSS点。高程按三等三角高程联测或收集已有成果。最小高程389.726 m，最大高程为468.147 m，平均高程411.015 m，地形起伏较大，为典型的丘陵地区。

区域二为川藏交界某大型水电站库区，平均海拔约4 000 m，为狭长带状高山峡谷区域，图2为该电站库区淹没影响区界桩测设三等GNSS控制网，共31个点。高程按三等三角高程联测。最小高程2 823.488 m，最大高程为3 677.108 m，平均高程3 050.609 m，地形起伏很大，属高山地区。

按照方案1和方案2分别对高程异常进行计算，并分别统计精度，计算内外符合精度，结果见表2和表3。

4.2 结果分析

从表2可以看出，方案1的高程异常差值最大值为5.38 cm，最小值为-6.55 cm；方案2的高程异常差值最大值和最小值分别是4.76 cm和-4.59 cm。在极值上方案2要优于方案1，两种方案的内符合精度分别是0.64 cm和0.62 cm，外符合精度为2.3 cm和1.97 cm，内符合精度两种方案相差不大，但外符合精度方案2要优于方案1。

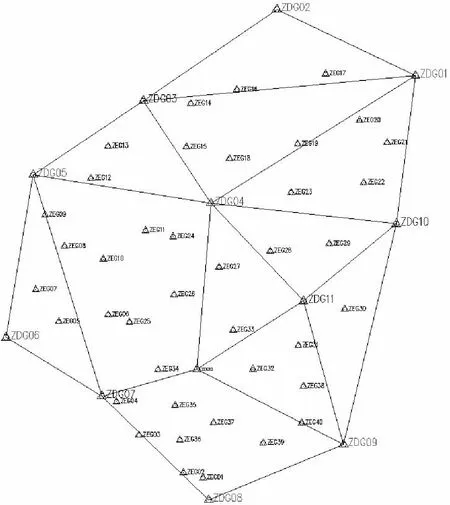
图1 区域一GNSS控制网分布示意 图2 区域二GNSS控制网分布示意

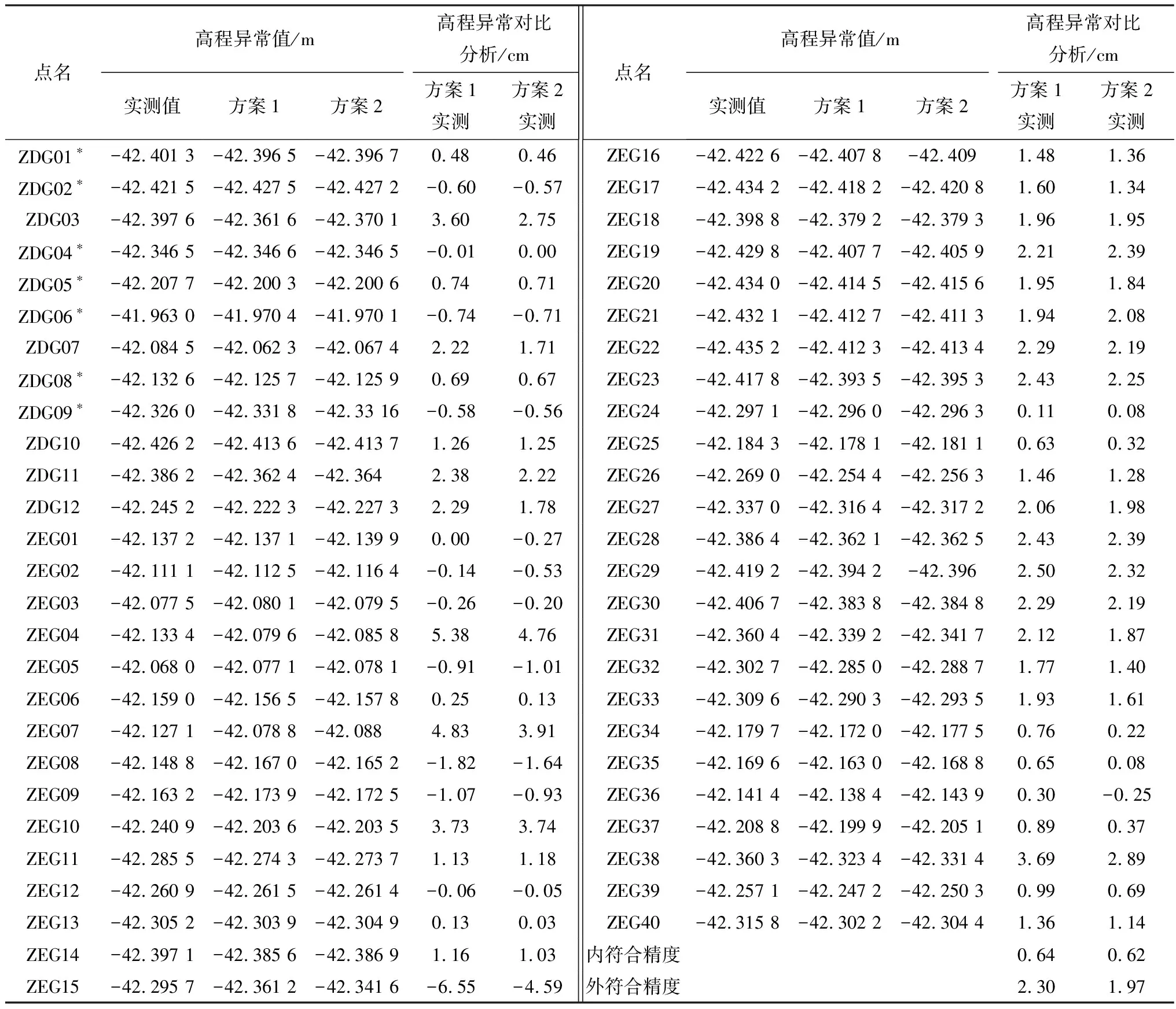
表2 区域一高程异常精度对比

注：点名带*号为已知高程异常点，其余作为检测点

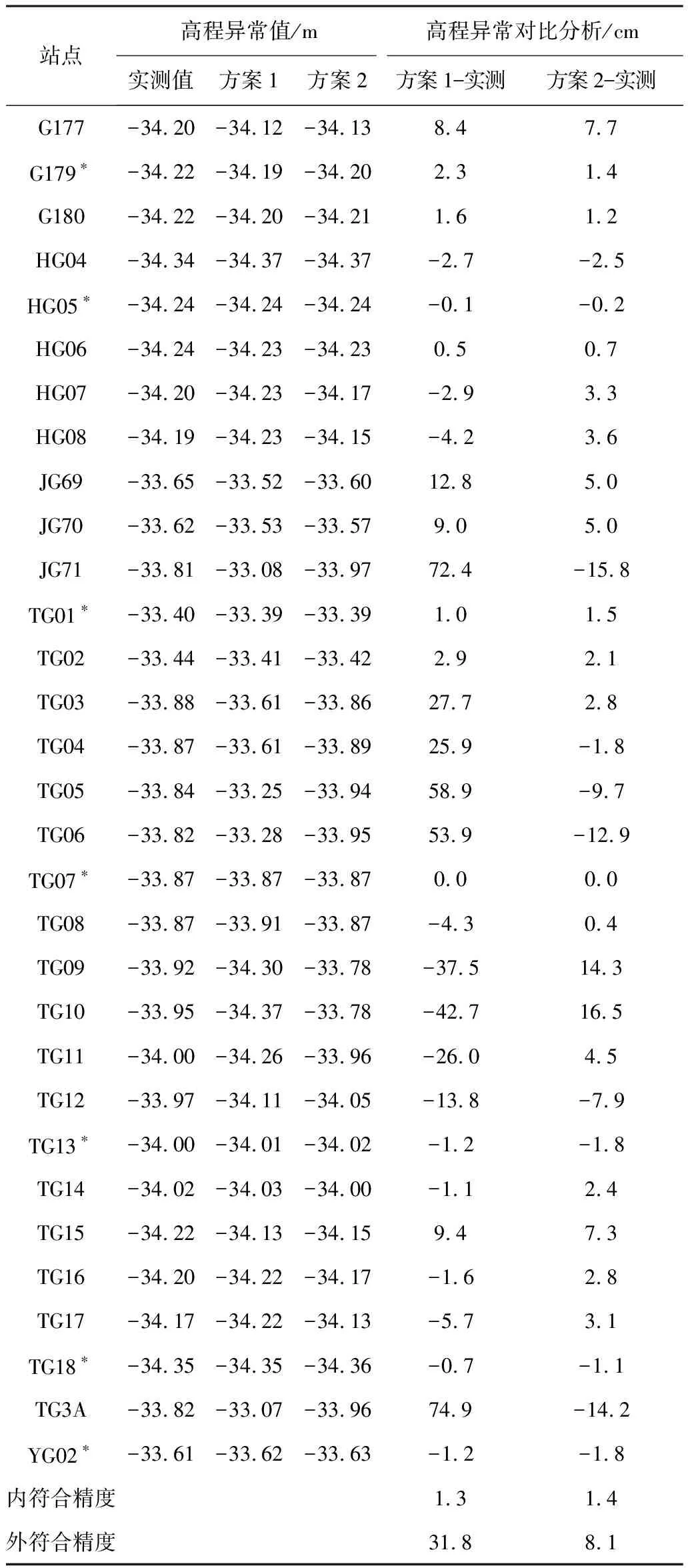
表3 区域二高程异常精度对比

注：点名带*号为已知高程异常点，其余作为检测点。

从表3可以看出，方案1的高程异常差值最大值和最小值分别是74.9 cm和-42.7 cm；方案2的最大值和最小值分别是16.5 cm和-15.8 cm。从极值上看，方案1远大于方案2，且稳定性差。两种方案的内符合精度相当，分别是1.3 cm和1.4 cm，但外符合精度方案2为8.1 cm，较方案1的31.8 cm提高很多。

通过对比表2和表3可以看出，相同方案下，无论是内符合精度还是外符合精度，区域一要明显优于区域二，这可能是由于大地水准面与地形条件有较强的相关性，区域一代表一般山区、丘陵地带，地形起伏相对平缓；区域二代表高海拔、地形起伏很大的山区。因而，区域一的整体精度要显著优于区域二。

5 结论及建议

本文基于EGM2008地球重力场模型，采用“移除-恢复”法，对在不同地形条件下获取GNSS水准数据求解高程异常，并对高程异常的精度进行统计分析，得出以下结论：

(1)基于EGM2008模型的“移除-恢复”法求解高程异常和常规的数值逼近法相比，内符合精度相当，但外符合精度有显著提高，在地形复杂的山区尤为明显；

(2)两种方法求解高程异常在地形起伏相对平缓区域的整体精度要优于地形条件复杂的区域；

(3)从极值上看，基于EGM2008模型的“移除-恢复”法精度更高、稳定性更好。

基于EGM2008模型的“移除-恢复”法在求解高程异常时受GNSS解算精度、EGM模型精度、点位分布等诸多因素影响，对地形条件复杂的大面积和长距离的区域还有待进一步研究，也可考虑采用分区和分段处理。