煤层气经济井网密度优化模型及应用
1. 中国石油大学(北京)工商管理学院, 北京 102249;2. 中联煤层气国家工程研究中心有限责任公司, 北京 100095
0 前言
煤层气开发主要是为了获取经济效益[1]。对于井网密度而言,地面工程、压裂、钻井等投资及成本都直接或间接与井数相关;而井网密度的大小直接影响采收率[2],继而影响煤层气销售的各种现金流入。井网加密,采收率升高,相应的收入升高;井网较稀,则井数较少,相应投资及建设成本也较小[3]。因此有必要使用折现现金流法建立经济井网密度优化模型,求取经济最优的井网密度。
1 折现现金流法简介
折现现金流法也称净现值法,以净现值作为评价指标,考察了全寿命期内项目的盈利能力,能有效体现开发项目效益,反映企业追求经济效益最大化的特点,在煤层气开发评价中是最为有效和可行的,也广为国内外企业接受[4]。计算公式为:
(1)
2 煤层气开发的经济效益
煤层气开发投资大、风险高,各投入与产出项计算方法的选取与精确程度直接关系到开发效益计算的准确性,进而影响到最优井网密度的确定以及开发投资决策。
2.1 基本计算公式
对于煤层气开发项目而言,主要现金流出项为勘探投资、地面工程建设投资、开发钻井投资、压裂工程投资、经营成本、利息税费及其他,主要现金流入项为销售、补贴及返税收入[5-7]。因此,煤层气开发项目经济效益的基本计算公式如下:
NPV=Rs+Rb+Rt-Ie-Id-If-Iz-Cj-Cl-
Ci-Tx
(2)
式中:Rs为销售收入,万元;Rb为补贴收入,万元;Rt为返税收入,万元;Ie为勘探投资,万元;Id为地面工程建设投资,万元;If为压裂工程投资,万元;Iz为钻井工程投资,万元;Cj为经营成本,万元;Cl为流动资金,万元;Ci为利息费用,万元;Tx为税费,万元。
2.2 受井网密度影响的现金流出
煤层气开发项目中钻井工程投资和地面工程建设投资占投资比例最大。对于井网密度而言,受其影响的现金流出项部分与井数有关,包括钻井投资、压裂投资及经营成本;部分与产气量有关,包括地面工程投资和税费。
2.2.1 钻井工程投资
开发钻井方面,煤层气与常规油气无本质区别,因此钻井工程投资计算公式[8]如下:
Iz=Ns×Czs=Ns×(CP+CN)
(3)
式中:Czs为单井折算钻井工程投资,万元/井;Ns为井数,井;Cp为垂直部分钻井支出,万元/井;CN为煤层气井水平部分钻井支出,万元/井。
2.2.2 压裂工程投资
根据常规油气压力成本核算相关文献,类比得到煤层气开采企业压裂工程投资的计算公式[9-10]:
If=Ns×INf=Ns×m×NF×(XF÷XF0)n
(4)
式中:INf为井均压裂成本,万元/井;m为每级压裂支出,万元/级;NF为井均压裂级数,级;XF为裂缝半长,m;XF0为基准的裂缝半长,m;n为由压裂规模决定的经验常数。
2.2.3 经营成本
根据相关学者研究成果总结,煤层气开采企业经营成本的计算公式[4-5,7]如下:
Cj=Ns×Cjs
(5)
式中:Cjs为单井经营成本,万元/井。
2.2.4 地面工程建设投资
对于地面工程建设,其部分费用与井数有关,但大部分费用与产气量正相关,因此选用单位产能地面工程建设投资对其进行计算。煤层气开采地面工程建设投资计算公式如下:
Id=N0×Rr×Idr
(6)
2.2.5 税费
煤层气开采企业经营税费的计算公式如下:
Tx=N0×Rr×fs×(P×ts)
(7)
2.3 受井网密度影响的现金流入
我国煤层气开发受国家补贴,2016年3月财政部发布了煤层气补贴新标准为0.3元/m3(原为0.2元/m3),对煤层气企业进行补贴,在中央财政补贴基础上,地方财政可给予适当补贴。我国煤层气企业实行增值税先征后返的优惠政策,煤层气项目退税收入可按销售收入的一定比例计算或者按照销项税减进项税的办法进行计算[11]。
2.3.1 销售收入
煤层气开采企业的销售收入计算公式如下:
Rs=N0×Rr×fs×P
(8)
2.3.2 补贴收入
煤层气开采企业的补贴收入计算公式如下:
(9)
式中:Sb为煤层气补贴费率,2018年为0.3元/m3。
2.3.3 返税收入
对煤层气开采企业的返税收入计算公式如下:
Rt=N0×Rr×fs×(P×tz)
(10)
3 井网密度对经济效益的影响
对于煤层气开发项目的经济效益,井网密度直接或间接地影响开发的现金流入与流出,一方面井网密度影响井数继而影响钻井工程投资、压裂工程投资及经营成本;另一方面通过采收率影响地面工程建设投资、税费、销售补贴及返税收入。厘清井网密度对井数和采收率的影响,可根据影响机制建立经济井网密度模型。
3.1 井网密度的影响机制
井网密度对煤层气开发的部分现金流入及流出项有直接或间接的影响,具体影响机制见图1。
据联合国教科文组织和联合国粮食及农业组织的不完全统计,全世界盐碱地面积已达9.554 38亿公顷。中国科学院南京土壤研究所最新研究显示,我国各种类型的盐渍土总量为9 913.3万公顷[1]。

图1 井网密度对煤层气开发经济效益的影响机制
3.2 井网密度对井数及采收率影响的量化

对于采收率而言,苏联著名学者谢尔卡乔夫建立的采收率和井网密度关系式,被公认为是能够较正确地反映采收率与井网密度的数量关系的经验公式[12]。谢尔卡乔夫公式为:
ER=ED×e-aS
(11)
对于煤层气而言,谢学恒等人[13]在传统的谢尔卡乔夫公式的基础上,考虑到煤层气开采的特点,建立了煤层气的井网密度-采收率修正公式。
Rr=R×e-zS
(12)
R=(Ci-Ca)/Ci
(13)
3.3 经济井网密度优化模型的建立
相同采收率情况下,不同的采气速度与产气曲线也会影响折现,进而影响净现值。为了避免井网密度优化模型无法显性表达,引入贴现调整系数对折现模型进行简化。因此,将式(3)~(10)带入式(2),结合式(1),则可建立井网密度与净现值的关系模型,及井网密度优化模型。
NPV=N0×(R×e-z×a×b)×{[fs×(P+Sb+P×tz
×(INf×ftf+Czs×ftz+Cjs×ftj)-Ie×fte
-Cl×ftl-Ci×fti
(14)
式中:ftin、ftd、ftf、ftz、ftj、fte、ftl、fti分别为收入及税费、地面工程建设投资、压裂工程投资、钻井工程投资、经营成本、勘探投资、流动资金、利息费用的贴现调整系数。
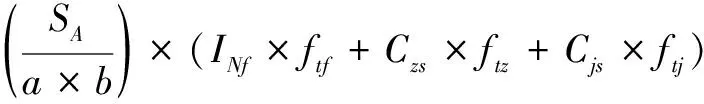
对于不同的产气曲线有不同的贴现调整系数,设N1为勘探年限;N2为开发年限;N3为产气年限。所以,对于收入、经营成本及税费而言,其每年的产气量是变化的,其贴现调整系数也依照实际情况随区块产气量不断变化,计算公式为:
(15)
式中:Nt为第t年产量,m3。
假设勘探投资均匀发生在勘探年限N1;钻井工程投资、压裂工程投资、地面工程建设投资均匀发生在开发年限N2;税费和利息均匀发生在产气年限N3;流动资金均匀发生于整个时期N1+N2+N3,在期末收回[14]。
基于以上假设,则可以计算出各投入和产出项的折现系数:
(16)
(17)
(18)

(19)
4 模型应用实例
4.1 示例区块基本情况
以沁水盆地南部斜坡带樊庄某区块为例[15],经济开采年限内不同井距情况下单井预测日产气量见表1。
表1经济开采年限内不同井距情况下单井预测日产气量

时间/a不同井距情况下产气量/(m·d-1)400 m×350 m350 m×300 m300 m×300 m300 m×250 m250 m×200 m14 3642 5761 5411 07658624 1124 1393 6623 2392 28733 0833 8103 7683 8043 17542 1593 2383 4543 5153 55351 7422 6363 0423 3303 42261 3612 1262 5652 9313 26071 0941 7762 1942 5603 08989011 5171 8962 2382 85197591 3511 6591 9702 600101 1951 4691 7482 364111 0491 3041 5502 134129361 1801 4001 949138411 0781 2741 787147619921 1681 645159181 0781 521168531 0011 413177929281 311188701 228198181 155207711 090211 03222980239292488625848
4.2 贴现调整系数及插值试算
经过计算,得到各投入和产出项的贴现调整系数,因计算较繁杂,故不列出计算过程,计算结果见表2。
表2各贴现调整系数计算结果

调整系数不同井控面积的调整系数值0.14 km2 0.105 km20.09 km20.075 km20.05 km2ftin0.550 30.458 40.407 10.369 30.325 0ftlt0.3170.3610.3910.4270.518fte & ftlr0.8930.8930.8930.8930.893ftd & ftz & ftf0.8450.8450.8450.8450.845
插值法实际运用最多,把可能的井距带入模型,计算得到NPV进行比较即可。鉴于煤层气经济井网密度优化模型计算量较大,而且插值之后可以减小搜索范围,避免搜索范围内双峰甚至多峰的情况[16],所以在模型运用中可以先使用插值法计算NPV,对于实例,选取0.05、0.075、0.09、0.105、0.14 km2进行插值,经计算发现0.105 km2有相对最优净现值,计算过程及结果见表3。
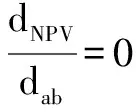
4.3 斐波那契法确定最优井网密度
以沁水盆地南部斜坡带樊庄某区块模拟数据为例,计算了不同井控面积下气藏井网特征系数Z值见表4。其中采收率由经济开采年限内累计产量计算得到,最终解吸程度用最大井网密度250 m×200 m开采最大年限25 a计算得到的采收率代替。拟合关系见图2。
表3插值法计算沁水盆地南部斜坡带樊庄某区块不同井控面积下净现值相关参数及结果
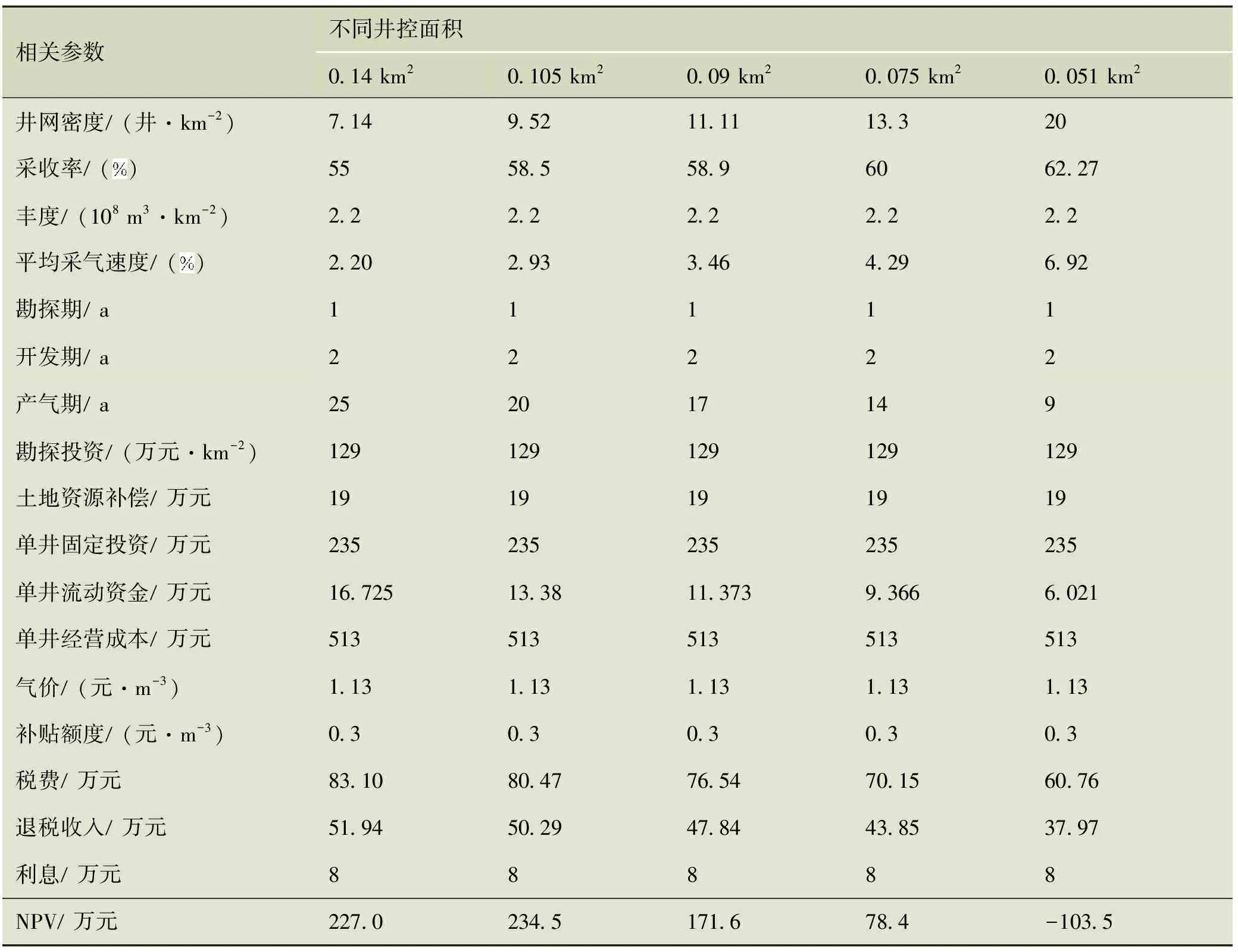
相关参数不同井控面积0.14 km20.105 km20.09 km20.075 km20.051 km2井网密度/(井·km-2)7.149.5211.1113.320采收率/()5558.558.96062.27丰度/(108 m3·km-2)2.22.22.22.22.2平均采气速度/()2.202.933.464.296.92勘探期/a11111开发期/a22222产气期/a252017149勘探投资/(万元·km-2)129129129129129土地资源补偿/万元1919191919单井固定投资/万元235235235235235单井流动资金/万元16.72513.3811.3739.3666.021单井经营成本/万元513513513513513气价/(元·m-3)1.131.131.131.131.13补贴额度/(元·m-3)0.30.30.30.30.3税费/万元83.1080.4776.5470.1560.76退税收入/万元51.9450.2947.8443.8537.97利息/万元88888NPV/万元227.0234.5171.678.4-103.5
表4沁水盆地南部斜坡带樊庄某区块Z值与井控面积的对应表
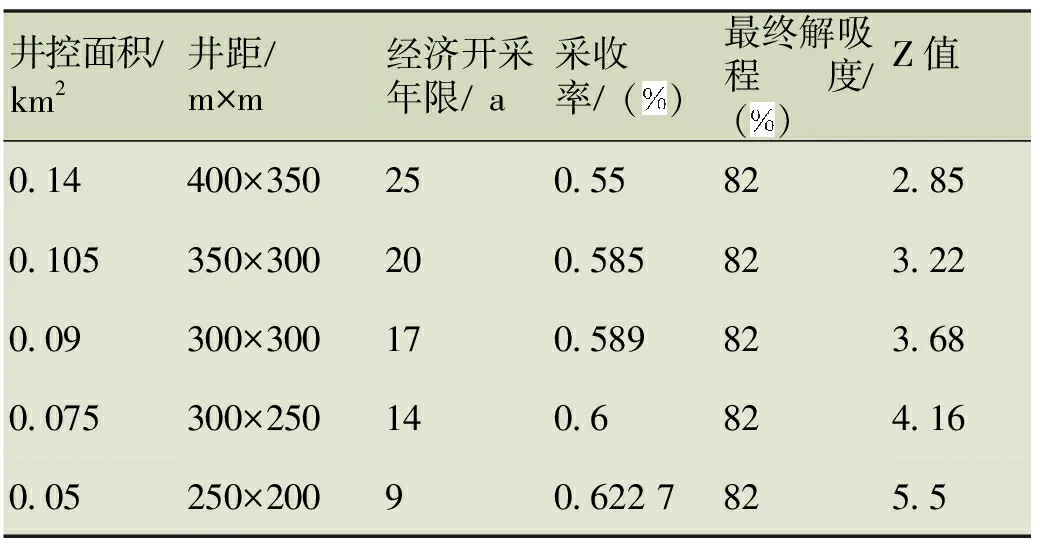
井控面积/km2井距/m×m经济开采年限/a采收率/()最终解吸程度/()Z值0.14400×350250.55822.850.105350×300200.585823.220.09300×300170.589823.680.075300×250140.6824.160.05250×20090.622 7825.5
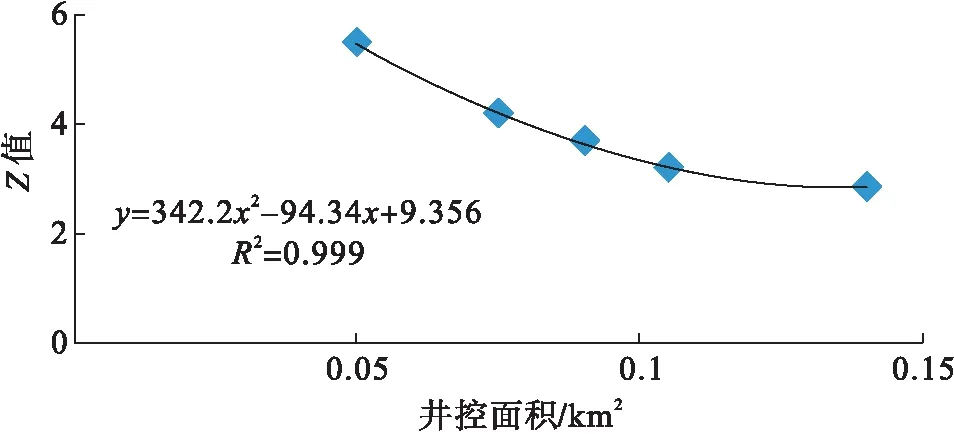
图2 系数Z与井控面积拟合关系
次迭代计算,当井控面积为0.115 km2时,NPV为236.4万元;此时极值点范围缩小为0.105~0.115 km2,若需求精度为0.01 km2,则经过迭代已经满足精度要求(若要求精度更高,则可继续迭代)。
在0.01 km2精度要求下,对于实例区块,最优井网控面积0.105~0.115 km2,最优井网密度8.7~9.5口/km2,在此范围内NPV保守估计量为227万元。相对极值点出现在0.11 km2处,此时NPV为250.80万元,应根据区块割理情况和地质条件,依实际情况合理选择横纵项井距,以达到最优净现值。
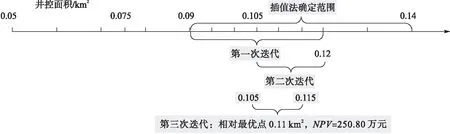
图3 经济最优井网密度迭代求解过程
5 结论
通过分析受井网密度影响的投入及产出因素,建立了煤层气开发各现金流入和流出项的计算公式,厘清了井网密度对煤层气开发经济效益的影响机制,以井数和采收率为纽带基于折现现金流法建立了煤层气经济井网密度优化模型,使用插值法和搜索算法以沁水盆地南部斜坡带樊庄某区块为例运用了该模型,得到以下结论:
煤层气开发井网密度由钻井数量直接影响钻井工程投资、压裂工程投资、经营成本和部分地面工程投资,通过采收率影响产气量从而间接影响销售收入、补贴收入和返税收入以及部分地面工程建设投资。
煤层气开发井网过密会导致投资巨大,投资回报率较低甚至难以回收投资;井网密度较小则会导致采收率较低从而造成资源浪费,并且损失资金的时间价值。因此,从煤层气开发全生命周期整体经济效益的角度精确优化井网密度,有助于降低成本,提高投资收益,辅助科学决策。
从技术经济学和财务评价的角度,煤层气经济井网密度优化方法可行,实例运用搜索求解证明该模型具有较好的适应性。在煤层气开发方案设计中,应结合实际资源约束和技术水平,考虑开发的经济效益,选取最优井网密度。

