p-y曲线法在基坑围护结构中的应用

，,2

(1.福州大学 环境与资源学院，福州 350116； 2.福州大学 地质工程福建省高校工程研究中心，福州 350116)

1 研究背景

p-y曲线反映的是地面以下横向推力桩的侧向位移y与土反力p之间的关系。 早在20世纪70年代， 国外学者就开始研究p-y曲线在海洋采钻平台结构物基础中的应用。 此后， Matlock[1]、 Reese等[2]、 Steven等[3]相继提出有关于软黏土和硬黏土的p-y曲线,其中Steven等[3]提出的p-y曲线合成法被美国石油学会API规范采用。 国内学者王国粹等[4]、 李卫超等[5]、 姚文娟等[6]， 黄茂松等[7]结合实际桩基础工程， 对不同土体中的p-y曲线进行修正， 进而提出新的p-y曲线模型。p-y曲线考虑了土体受到荷载作用时的非线性变形， 能够如实地反映出地面以下土体的应力状态[8]。 相对于弹性地基梁法，p-y曲线考虑了桩前土体可能出现的非弹性变形， 理论上更符合桩土之间相互作用的实际情况。 目前国内学者主要利用p-y曲线研究横向推力桩在桩周土体未开挖情况下的变形及内力， 很少将p-y曲线应用于计算基坑围护结构等桩周土体开挖情况下的位移。 朱碧堂等[9]、 朱彦鹏等[10]、 邓子胜等[11]利用p-y曲线研究了深基坑中桩土之间的相互作用力， 但他们都局限于理论分析， 没有结合工程实例验证p-y曲线法计算基坑围护结构内力和变形的合理性。

本文采用考虑土体非线性位移的p-y曲线法分析基坑面以下土体的应力状态，并且结合工程实例，通过p-y曲线法的计算值、弹性地基梁法的计算值与实测值进行对比，分析p-y曲线法计算基坑围护结构位移的适用性。

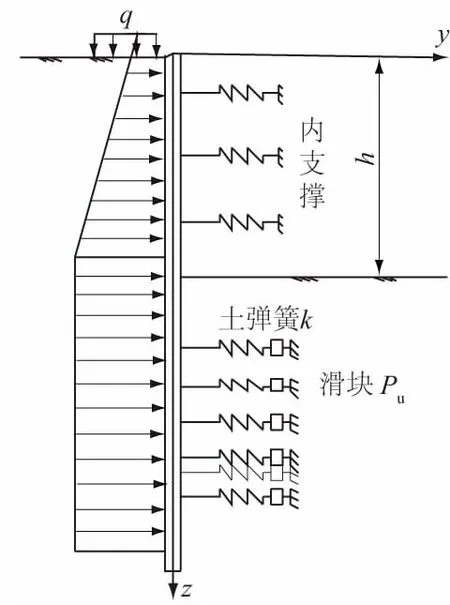
图1 p-y曲线法分析简图Fig.1 Brief analysis diagram of p-y curve method

2 p-y曲线法计算基坑围护结构的原理

2.1 理想弹塑性模型

采用p-y曲线法计算基坑围护结构位移时，考虑到土体的非线性位移，可将土的抗力视为2部分：土弹簧(系数k)抗力与滑块抗力Pu[9]。当基坑面以下土体刚受到围护结构侧向挤压变形较小、处于弹性状态时，可当作是一个土弹簧，土抗力P随着地基土水平反力系数k线性增长；当土体侧向挤压变形过大、进入塑性状态时，可将土体当作一个滑块，此时土抗力达到极限值Pu不再变化(如图1所示)。

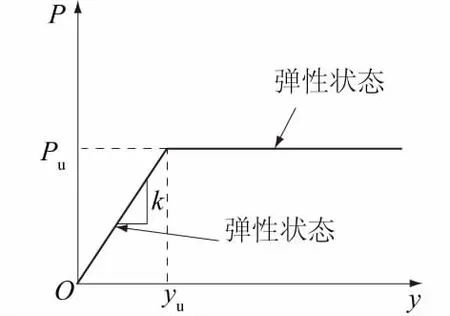
图2 理想弹塑性模型Fig.2 Ideal elastic- plastic model

一些学者利用试验拟合得出了不同的p-y曲线模型，其中朱碧堂等[9]利用理想弹塑性p-y曲线模型对工程实例进行分析，得到的计算值符合实际结果。结合以上思路，本文p-y曲线模型选用理想弹塑性模型(如图2所示)，表达式见式(1)。当围护桩(或墙)周围的土体受到挤压处于弹性状态时，土抗力P与土体位移y成正比；当土体位移y达到塑性范围yu时，土抗力P达到Pu后将不再变化。

2.2 地基土水平反力系数k

当土体仍处于弹性状态时，土体的水平反力系数常用m法进行计算[12]。现行《建筑基坑支护技术规程》(JGJ 120—2012)[13]中基坑内侧土体的水平反力系数k的计算式为

k=m(z-h) 。

(2)

式中：m为土的水平抗力系数的比例系数；z为计算点距地面的深度；h为计算工况下的基坑开挖深度。

其中m值宜按桩的水平荷载试验及地区经验取值，缺少试验与经验值，也可按经验公式计算[12]。本文采用m法确定地基土水平反力系数k的取值。

2.3 统一极限抗力Pu

关于桩前土体的极限抗力，国内学者进行了诸多研究[14-15]，本文采用的是通过参数选取拟合现有极限抗力的统一极限抗力，表达式为[15]：

Pu=AL(α0+x)n，

(3)

AL=Np(γsd或Su)d1-n。

(4)

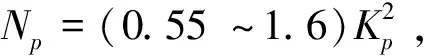
2.4 基坑围护结构迎土侧土压力计算

基坑围护结构迎土侧土压力的计算，按照现行《建筑基坑支护技术规程》[13]中的相关规定进行。

2.5 基坑围护结构变形计算

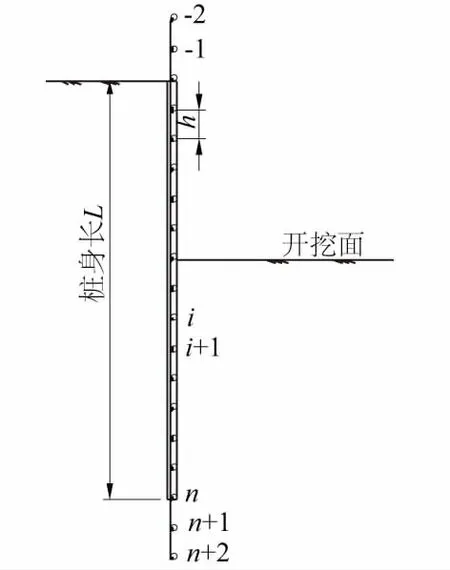
图3 基坑围护结构 散点简图Fig.3 Scatter plot of the deep foundation ditch enclosure structure

基坑围护结构的曲线微分方程很难直接计算出围护结构的位移，因此本文利用有限差分法结合曲线微分方程，采用软件MatLab编制迭代程序计算出方程的解。首先，沿桩身方向将桩平均分成n个单元，各节点编号为0，1，2,…,n-1，n，每个单元长h；然后，在桩顶与桩底处分别增加2个虚设的点-1，-2和n+1,n+2;再利用有限差分法的原理，将曲线微分方程表示为式(5)；最后计算方程式，得出位移值。基坑围护结构散点见图3。

yn-2-4yn-1+cnyn-

(5)

式中：yn为桩身第n节点的位移；cn=6+(kib0h4)/(EI)，其中ki为基坑面以下土体的水平反力系数，b0为土抗力计算宽度；EI为围护桩(或墙)的抗弯刚度；bs为主动土压力计算宽度；h为桩身每个节点的间距。

利用MatLab软件编制迭代程序计算式(5)的位移，迭代法思路如下：

(1)将ki代入式(5)中，计算得到每个节点位移yi。

(2)对照p-y曲线模型，当yi

(3)将新得到的ki代入式(5)，计算得到位移yi+1。

(4)重复(1)—(3),使前后计算得到的位移yi和yi+1的误差在允许范围内(前后位移差值在1 mm以内时，认为迭代收敛)。

3 工程实例验证

本文第2部分介绍了p-y曲线法计算基坑围护结构位移的基本原理和方法，分析表明：计算基坑围护结构位移时，采用p-y曲线法能更好地考虑基坑面以下土体的变形状态，符合桩土之间相互作用的实际情况，与传统基于弹性地基梁理论计算方法相比更加合理。

基于弹性地基梁理论的基坑围护结构内力、位移计算方法中，增量法是大家公认的较为符合工程实际的方法[12]。本部分将结合工程实例，通过p-y曲线法、弹性地基梁增量法计算值及其与实测值的对比，验证p-y曲线法计算基坑围护结构位移的合理性。

图4 地铁站基坑围护结构 横断面图Fig.4 Cross section of the deep foundation ditch enclosure structure of subway station

3.1 工程概况

福州某地铁站站台采用明挖法施工，基坑主体围护结构采用厚度0.8 m的地下连续墙，围护墙深度约31.5 m。内支撑由第1道的C30钢筋混凝土支撑和第2，第3，第4道的钢支撑组成。基坑支护形式如图4所示。

地下连续墙深度范围内地层由上至下依次为素填土、淤泥、淤泥质土。各土层的物理力学参数如表1所示。

表1 各土层的物理力学参数Table 1 Physical and mechanical parameters of soil strata

在基坑开挖前对基坑进行降水，使地下水稳定在基坑开挖面以下0.5～1.0 m范围内。基坑施工主要工况的基本情况见表2。

表2 地铁站基坑开挖的主要工况Table 2 Main working conditions of pit excavation for subway station

3.2 围护结构侧向位移计算

根据钢筋混凝土支撑与钢支撑的材料性质、截面面积、分布距离等设计参数，并依照《建筑基坑支护技术规程》[13]算出各内支撑的水平刚度系数KT，如式(6)所示，结果见表3。

(6)

式中：α为内支撑松弛系数；E为内支撑材料的弹性模量；A为内支撑构件的截面积；b0为计算宽度；L为内支撑长度；S为内支撑构件的分布距离。

表3 支撑刚度系数KTTable 3 Horizontal stiffness coefficient KT of bracing

根据《建筑基坑支护技术规程》[13]中的规定，本段基坑围护结构上的主动土压力计算宽度bs=1.0 m，土反力计算宽度b0=1.0 m。根据《天津市建筑基坑工程技术规程》[16]中各类土水平反力系数的比例系数m值的参考值及本地经验值，本段基坑m取2 MN/m4。根据本地土层条件，α0=0.4，n=0.7，Np=2.2。

在基坑ZQT4,ZQT6,ZQT10断面的地下连续墙中埋设测斜管，利用测斜仪在竖向方向每隔0.5 m监测施工过程中地下连续墙的侧向位移。根据以上参数及规范，可以得到p-y曲线法、地基弹性梁增量法计算出的基坑围护结构侧向位移，将其与实测值绘于图5。

图5 围护墙侧向位移Fig.5 Lateral displacements of retaining wall

从图5可看出：

(1)在地铁站基坑工程工况3、工况4时，增量法与p-y曲线法计算的基坑围护结构位移曲线形态与实测位移曲线形态相似，说明增量法与p-y曲线法的计算结果都能很好地反映围护结构受力的变形规律。

(2)在地铁站基坑工程工况3、工况4时，与增量法相比，p-y曲线法的计算结果无论是侧向位移曲线的形态，还是最大位移的数值及出现位置均更加接近实测值。

从表4可看出：增量法计算得到的位移最大值在不同算法和实测值中是最小的，p-y曲线法计算得到的位移最大值大于增量法的位移最大值，且更接近实测位移最大值。因此，p-y曲线法的计算结果更符合工程实测值。

3.3 计算结果分析

从工程实例计算结果可以看出，p-y曲线法与弹性地基梁增量法都适用于计算基坑围护结构的位移，但相对于地基弹性梁增量法，p-y曲线的计算结果更接近实测值。

表4 不同计算方法与实测的最大位移值Table 4 Maximum displacement obtained by measurement and different calculation methods in different working conditions

在实际工程中，特别是在软土地区，深基坑围护结构的侧向位移往往高达几十毫米，超过了软土弹性变形的范围，因此在计算基坑围护结构位移时应考虑土体变形已进入塑性状态。大量的分析表明[17-18]，在荷载作用下桩周土体变形增大，土体可能达到屈服，进而进入塑性状态。基于弹性地基梁理论的计算方法认为，基坑开挖面以下土体变形始终处于弹性变形，这与实际情况不尽相符。p-y曲线法考虑了土体非线性位移，当达到塑性状态时，土抗力不再变化，与土体实际的受力变形状态接近。计算实例中基坑面以下的软土受围护结构挤压的侧向位移较大，已进入塑性状态。弹性地基梁法计算时仍然认为土体是弹性变形，p-y曲线法则考虑了软土的塑性变形，因此计算结果比基于弹性地基梁理论的增量法更接近实测值。

4 结 论

(1)基坑围护结构受力变形时，开挖面以下邻近围护结构的受压土体初期处于弹性变形，但随着围护结构侧向位移的增大，可能进入塑性状态，因此在计算基坑围护结构位移时考虑土体的非线性变形是必要的。

(2)本文利用p-y曲线结合理想弹塑性模型与统一极限抗力，较好地模拟了土体的受力变形状态，并且利用有限差分法计算出基坑围护结构的侧向位移。

(3)p-y曲线法能更好地考虑基坑开挖面以下土体可能进入塑性状态的实际情况，与传统的基于弹性地基梁法的计算方法相比，理论上更加合理。本文基于工程实例的计算结果也表明，与弹性地基梁增量法相比，无论是围护结构侧向位移曲线的形态，还是最大位移的数值和出现位置，p-y曲线法的计算结果均更加接近实测值。理论及实践均表明，p-y曲线法计算基坑围护结构侧向位移是合理的。