基于格子Boltzmann法的树木流场数值模拟

，

(1.湖南大学土木工程学院， 湖南长沙410082；2.湖南大学建筑安全与节能教育部重点实验室， 湖南长沙410082)

0 引言

树木对气流的阻力可以改变风速和临近区域的风向，从而影响风环境，而且对行人、其它树木和建筑物有一定的防护作用。所以，研究树木对风环境的影响具有重要的意义。随着计算机技术的发展，国内外很多学者做了树木风场的数值模拟研究，提出了一些树木简化模型：文献[1]将树冠简化为2.5 m高，阻力系数为0.3，叶面积密度为2.1 m-1的长方形来研究二维树冠内外的流场分布；文献[2]把树木看成实心圆柱树干和圆锥体多孔树冠的组合，并通过试验证明均匀二维绕流流场在树木遮蔽区的计算结果没有三维模拟准确；文献[3]采用孔隙率模型将树冠简化成半径2 m，高2m的半球，树干宽15 cm，高10 m，从绿化范围和绿化与建筑的间距研究利用绿化改善住宅周围环境的优化方案；文献[4]采用附加UDF源项法模拟树冠的多孔介质特性，将树冠简化为多孔区域，辅助于树冠动量源项、湍动能源项和耗散率源项，并通过改变树冠与建筑间距的方式研究树冠对建筑周围风环境的改善作用。

格子Boltzmann法起源于格子气自动机(Lattice Gas Automata，LGA)，其最本质的特征在于完全的并行性和纯布尔运算。文献[5]为简化碰撞算子提出单松弛模型(LBGK)并列出了DdQm系列模型(d维空间，m个离散速度)，该模型简化了碰撞项而大大减少了计算量，但随着雷诺数的增大，LBGK模拟结果会不稳定。为此，文献[6]细致分析了多松弛模型。1994年，文献[7]将大涡模拟引入到LBM进行了高雷诺数的方腔流模拟，即直接模拟大尺度结构，由函数过滤掉的小尺度结构对大尺度结构不敏感依赖，用亚网格模型(subgrid Scale，SGS)来模拟。多孔介质流动的LBM主要有孔隙尺度和表征体元(representative elementary volume，REV)尺度的问题，对于树木这样的大孔隙实际问题，不关心孔隙流动细节、获得平均体积宏观流动的REV则更加适合。关于等温不可压缩多孔介质问题，文献[8]提出的模型包含线性阻力和粘性项，多孔介质的影响通过施加外力得到Stokes或Brinkman方程，结构函数特性由经验给出；在此基础上，文献[9]提出了求解包含线性阻力、黏性项和非线性阻力项的通用渗流模型的REV尺度渗流的广义LBE模型(GLBE 模型)。该模型的平衡分布函数和作用力项中均包含反映介质特性的孔隙率，而且对渗流速度大小没有要求,此模型不存在离散误差，可得到准确的宏观方程。本文建立REV尺度的树木多孔模型，由多松弛时间格式(multiple relaxation times，MRT)的格子Boltzmann模型(MRT-LBE)结合大涡模拟(large eddy simulation，LES)计算分析该树木模型在风荷载下的流场。LBM的算法并行性高、求解速度快、加之计算结果可靠等优势，使其有望成为一种高效的用于解决树木风场等实际问题的数值模拟方法。

1 数值方法

1.1 流场计算的MRT-LBE模型

由于雷诺数的增大，传统的单松弛模型模拟的结果会变得不稳定，为此，文献[10]提出了MRT-LBE模型，该模型用多个松弛时间参数来描述各粒子趋于平衡态的速度，其演化方程为

(1)

式中,fα(x,t)是时刻t、位置x处、α方向的离散密度分布函数，δt是时间步长，eα是粒子离散速度，采用二维九速D2Q9模型，则各个方向的速度配置为：

(2)

其中，单个粒子的迁移速度c=δx/δt，δx和δt分别为网格步长和时间步长，通常取δx=δt=1。S是动量空间碰撞对角阵：

S=diag(s0,s1,s2,s3,s4,s5,s6,s7,s8)，

(3)

本文中s0=s3=s5=0；s1与体积黏性ζ有关，ζ=(1/s1-1/2)/3，取s1=1.2；s2=s4=s6=1.1；s7、s8与运动黏性系数υ有关，s7=s8=2/(6υ+1)。变换矩阵M是用来实现参数在动量空间和速度空间转换的，形式如下：

(4)

粒子分布函数fi(x,t)映射到矩空间：

m=Mf,f=M-1·m，

(5)

式中，m是空间的矩，M-1与M互为逆矩阵。粒子平衡态分布函数对应的矩空间平衡态函数为

(6)

(7)

(8)

1.2 求解表征元尺度多孔介质内流动的LBM模型

通过求解广义Navier-Stokes方程的MRT-LBM模型，计算REV尺度多孔介质内的流动，演化方程如下：

(9)

式中，I是单位矩阵，粒子平衡态分布函数为

(10)

ε是多孔介质孔隙率，作用力Fi计算如下

(11)

(12)

(13)

Fx，Fy分别是F在x,y方向的分量，渗流密度、速度、压力定义为

(14)

因为F含有流动速度u，所以方程(14)是速度u的二次非线性方程，直接求解得

(15)

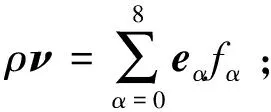
(16)

MRT-LBM计算过程如下：

在矩空间计算粒子碰撞的分布函数

(17)

在速度空间进行粒子迁移

(18)

1.3 湍流在LBM中的实现

采用非均匀盒式过滤器，将流场分布函数以Δ为过滤尺度分为可解和不可解部分。其中，湍流尺度大于Δ的称为可解部分；湍流尺度小于Δ且经过滤器平均化的小尺度部分称为不可解部分。非均匀盒式过滤器的滤波函数为

(19)

式中，Δ为滤波宽度，一般取网格划分的最小格子尺寸。为了得到大尺度运动的控制方程和小尺度运动的封闭模型，本文采用Smagorinsky模型[11-12]构造亚格子应力模型来辅助求解，相应的亚格子应力为：

(20)

(21)

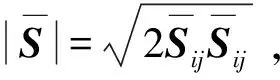
υ=υ0+υt，

(22)

式中，υ0是物理粘性系数。

1.4 相对风压和风压系数的计算

用无量纲的压力系数Cp表示树木周围的压力大小。压力系数计算公式如下：

(23)

其中，Ur是10 m处的来流初始速度，取0.01；ρr是来流初始密度,取1.0；w是相对风压值，公式如下：

w=p-p0，

(24)

2 数值模拟及结果分析

2.1 问题描述和参数选取

尽管二维模型没有三维模型在描述问题上来的真实，但树木绕流主要研究的是树木周围的流动，可以忽略树木内部的三维几何细节，这样也大大减少了计算量[13-14]。整体来说，只要参数选择合理，树木三维风场通常可简化为二维问题。本文采用文献[15]中的树木模型，模型尺寸及入口平均风剖面如图1，将树冠背风面延长线与地面的交点定为坐标原点，树冠简化为直径为2 m，高5.8 m的圆柱体，整个树木总高为7 m。

计算域如图2，整个流域大小(D+19H)×5H，计算域入口边界速度如图1，其他三面∂u/∂n=0(n为边界的法向)，边界分布函数采用非平衡外推格式[16]。孔隙率和渗透系数可以根据阻力系数确定，具体见文献[17-18]，树冠和树干孔隙率分别取0.74和0.9，达西数0.01。本文模拟的雷诺数为10 000，设置收敛标准为

(25)

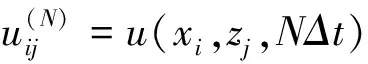
图1树木计算模型图示
Fig.1Schemeofnumericalmodelofwindbreakflow

图2计算区域图示
Fig.2Computationaldomain

2.2 树木周围流场的速度和流线分析

图3给出了树木遮蔽区下游不同位置处，数值模拟的平均风速与试验结果和CFD(computatinal fluid dynamics)结果[20]的对比，该实验数据是Y Kurotani等在松树尾流处实测的值(KUROTANI Y， KIYOTA N， KOBAYASHI S.Windbreak effect of Tsuijimatsu in Izumo Part.2[C]//AJJ Environmental Engineering I.[S1]: Architectural Institute of Japan, 2002)，本文将该松树简化为多孔介质，在树木中心截面处进行二维的LBM模拟计算，用亚网格模型解决了实际情况的湍流问题。其中UH是H高度处的入口平均风速，可以看出本文的计算结果与试验基本吻合，树木的遮挡也大大降低了下游的风速。与实测结果相比，LBM算得的平均风速大一些，但趋势都是一致的，即在树顶附近速度突然增大，树后风速最大值出现在较为稀疏的树冠下面z≈0.25H处(如图3(a)-(b)所示)和树冠顶面z≈H处(如图3(c)-(e)所示),最小风速出现在树冠的中间位置。

与CFD计算结果相比，LBM算得的结果更符合实测结果，说明了LES-LBM的优越性：LBM是以介观动力学模型为基础的介观方法，假设条件较少，与基于宏观模型的CFD方法相比，在处理多尺度的复杂流动问题中具有较大优势；其次就湍流模拟方法来看，CFD结果所用的雷诺平均法精度普遍低于大涡模拟，尽管结果是时均速度，但是与大涡模拟相比，雷诺平均法过滤了太多的脉动信息，必然更加背离现实情况。由于文献给出的信息有限，有些参数用估算和试算的方法大致确定给模拟结果带来了误差。

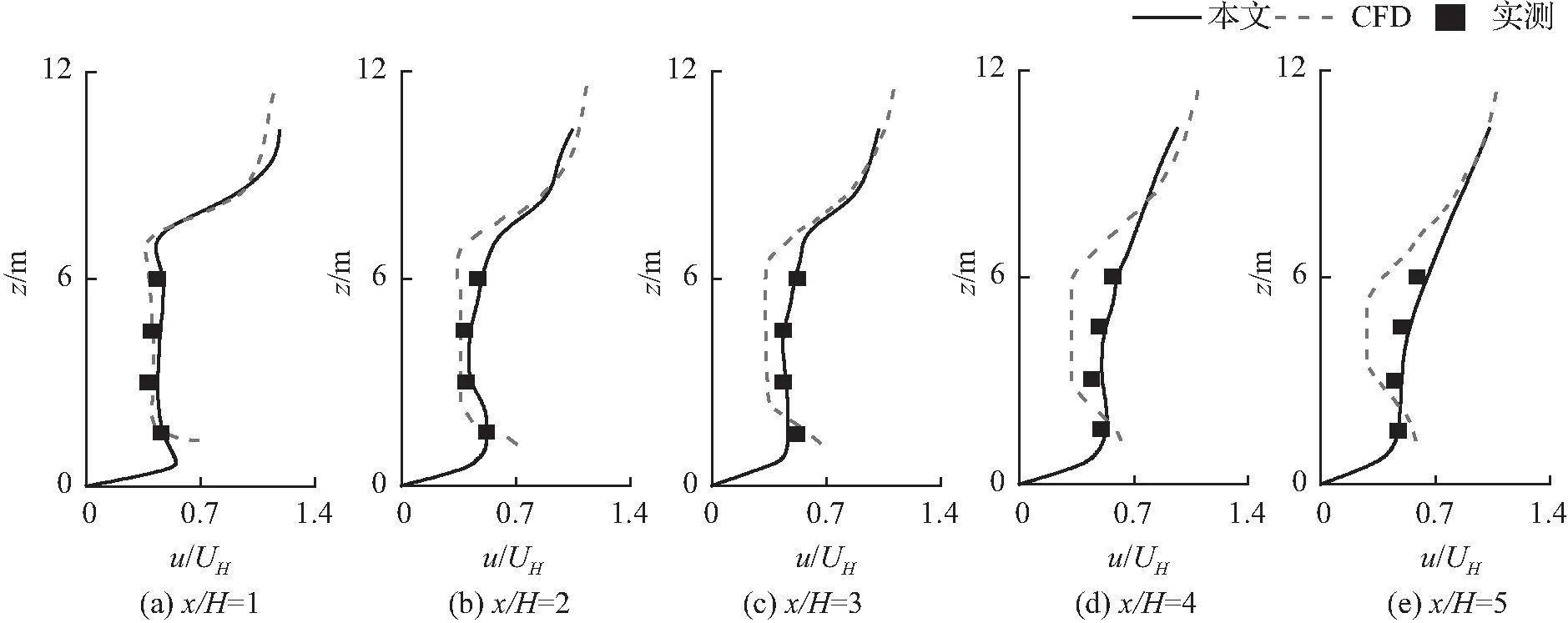
图3 树木下游不同位置速度剖面的比较Fig.3 Comparisons of the mean velocity profiles at differentlocations backward the tree

图4 水平速度和流线图/(m·s-1)Fig.4 Horizontal velocity distributions and streamlines/(m·s-1)

计算收敛之后，流场的水平速度和流线如图4所示，气流受到树木的影响使风速由树冠迎风面开始向后逐步递减，在树冠中间高度处(z≈0.6H)，树冠迎风面水平风速3.57 m/s，背风面3.18 m/s，与该高度处的入口平均速度相比分别降低了24 %和32 %；在树木上方3 m高度范围内风速很大，最大水平速度约为1.3倍的来流速度〈ub〉，实际情况中越接近树冠顶面，由于树叶拖拽力明显，就会加剧涡流的变化；树木后面的水平速度分层很明显，树干高度范围内的风速层明显比树冠后的风速大，这和介质的透风性能有关。气流撞击树木表面，从中穿过而避免形成高压气幕，树冠介质的阻碍让风向也产生变化，流线经过树冠向后呈放射状，但并没有产生大的旋涡，这说明树木对风荷载不仅有很好的阻挡作用，还有一定的疏散作用。

2.3 树木周围流场的风压分析

图5是树木周围的相对风压云图，可以看出树冠前方和迎风面主要是正压，气流撞击树冠使得迎风面产生很大的正压力，迎风面上方角点处出现了压力逐渐减小的过渡；风压的最大绝对值主要在迎风面和背风面附近，压力在树冠内部沿着x轴方向由正转负，树木后方压力很小。将图片放大到树木附近如图6所示，风压系数从树冠迎风面到背风面显示出明显的变化梯度，但在树冠下面和树干表面，分层不明显，气流流动不稳定；树冠迎风面风压系数中间大两边小，z=0.6H处的迎风面上有最大正压系数0.327，这是由于在该位置受到多孔介质的阻碍，风速减小，由伯努利方程可知，同一流线上风速越小压力越大，所以附近风速减小并转化的风压值最多，背风面风压系数分布规则同迎风面，最大负压系数为-0.117。树冠顶面前缘处最大风压系数约为0.103，后缘-0.037，整个树顶的风压系数变化不大，这是因为气流在树顶前缘处分离，而平均风剖面的影响会使风能转化成更多的动能，但是稀疏的树冠有效地耗散了这些能量，从而避免树顶产生明显的涡流。

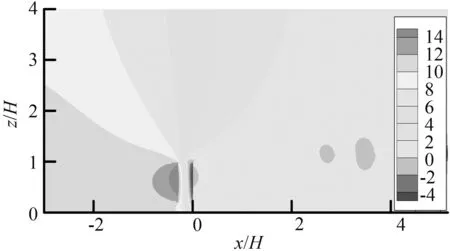
图5压力云图(Pa)
Fig.5Pressuredistributions(Pa)

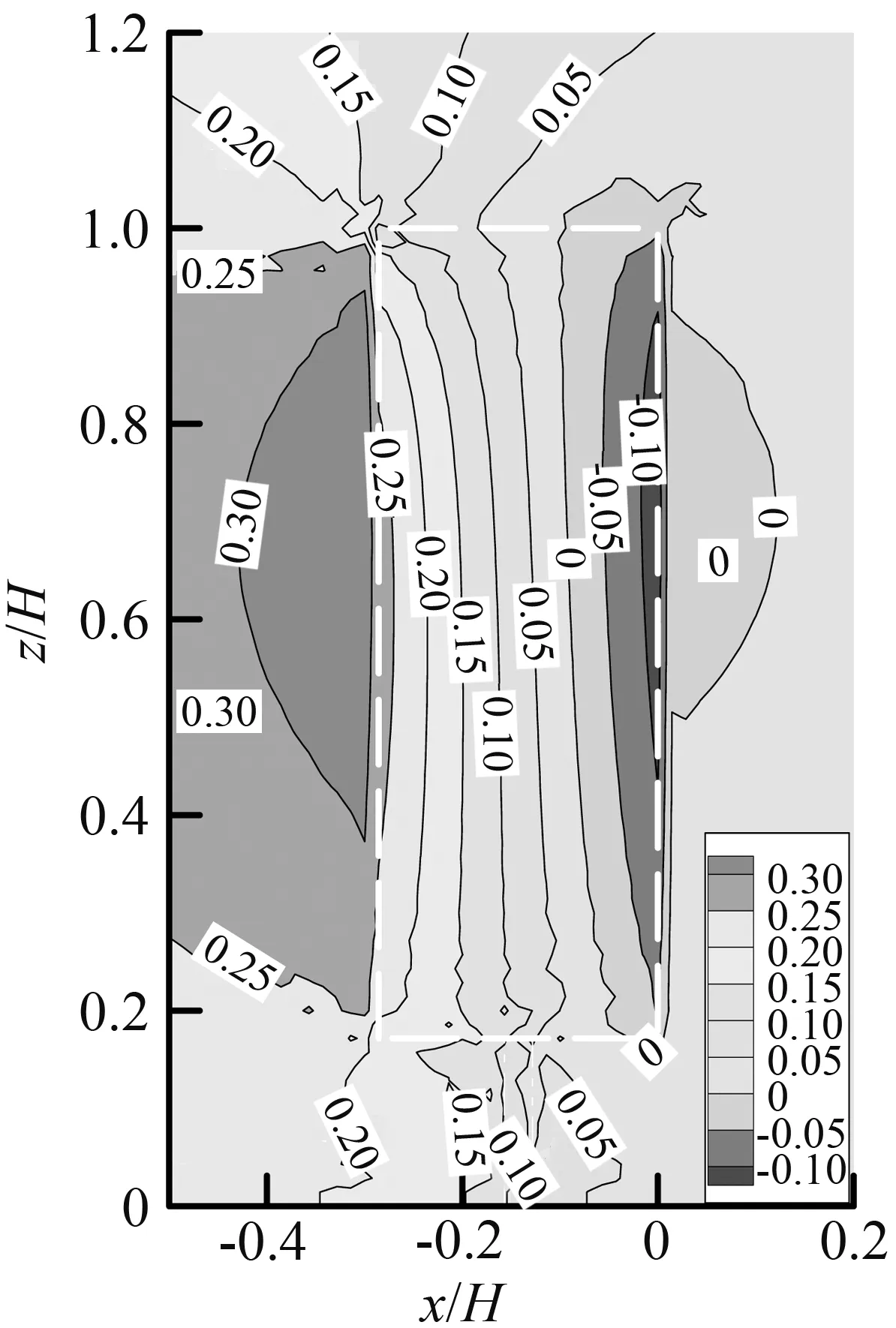
图6树木附近平均压力系数图
Fig.6Meanpressurecoefficientnearthetree

2.4 B类地貌下的应用示例

按GB50009-2012《建筑结构荷载规范》，以B类地貌为研究对象，地面粗糙度指数为0.15[22]。先在模型前端12H处设置一格栅，该格栅下密上疏，能在流场中制造扰动，格栅前端入口处风剖面为Uz=u10(z/10)0.15,u10设为10m/s。图7和图8分别是格栅布置图和模型前模拟所得的来流平均风速、湍流度剖面，其中，模拟的来流风速剖面与Uz=u10(z/10)0.15(这里u10取12 m/s)近似符合，模拟的来流湍流度剖面也与B类地貌下的湍流度剖面基本吻合。

图7格栅布置图
Fig.7Gridlayoutintensityprofile

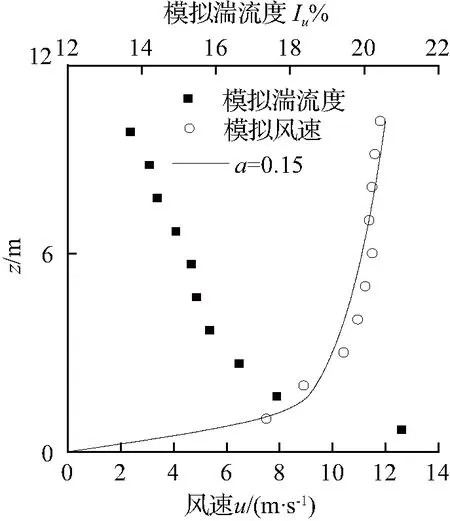
图8平均风剖面和湍流度剖面
Fig.8Meanwindspeedprofileandturbulence

图9给出了模型遮蔽区下游不同位置处的平均风速剖面，可以看出该风速剖面的变化趋势与图3类似，由于能量从树顶层传递至底层，风速随着高度的增加逐渐增大；在z

(a) x/H=1(b) x/H=3(c) x/H=7(d) x/H=14(e) x/H=21

图10是树木下游不同位置的湍流度剖面，因为树木边界层剪切应力引起较大的湍动能，所以树木顶部和底部的湍流度较大，如图10(b)，树底面(z=1m)和树顶(z=7m)最大湍流度分别可达33 %和20.8 %，与图10(e)中相应值对比分别提高了65 %和41 %。由图10(a)-(c)可以明显看出，z<0.6H时，湍流度随高度的增加而急剧减小，之后直到z=H湍流度又逐渐增大到一个极大值，随着下游位置与模型的水平距离越来越远，该趋势会逐渐减弱直至消失，即湍流度会减小并与来流湍流度剖面慢慢重合(如图10(d)～(e)所示)，根据文献[22]的研究，树木对湍流的影响会持续到大约x=50H的地方。

(a) x/H=1(b) x/H=3(c) x/H=7(d) x/H=14(e) x/H=21

3 结语

采用多松弛格子Boltzmann模型结合大涡模拟对树木流场进行高雷诺数下的数值模拟，将下游平均风速与试验结果和CFD模拟结果进行对比，比CFD结果略大，与试验吻合良好，可以准确预测最大风速的位置，说明LBM具有一定的优越性。并将该树木模型结合格栅设置模拟了B类地貌下的树木流场，选择计算结果收敛后的数值分析，模拟结果表明：

① 树木在风作用下可以有效降低迎风面和背风面附近的风速，但树冠顶面3m范围内最大水平风速高达1.3倍的来流风速，树高范围内的最大水平风速出现在较为稀疏的树冠底部。树冠介质的阻碍让风向也产生变化，流线经过树冠向后呈放射状。

② 树木周围的风压变化显著，形成明显的风压梯度，但树冠下面和树干表面，分层不明显，气流流动不稳定。风压的最大绝对值主要在迎风面和背风面附近，整个树顶的风压系数变化不大。

③ B类地貌下的模型下游风速在树顶以下均会有所减小，树顶以上的风速均呈增大趋势。下游位置与模型的水平距离越来越远，风速剖面就愈加接近来流风剖面，树木的遮蔽效果越来越小。树木下游湍流度极大值，出现在树木顶部附近，随着下游位置与模型的水平距离越来越大，湍流度会减小并逐渐与来流湍流度剖面重合。