MCR-WPT负载对系统最优参数的影响
蒋林枭,陈海川,2*,倪 陶
(1.西华大学电气与电子信息学院, 四川 成都 610039;2.物理场生物效应及仪器四川省高校重点实验室, 四川 成都 610225)
无线电能传输是近几年来兴起的一种新型电能传输方式。2007年麻省理工学院(MIT)教授Marin Soljacic利用磁谐振方法,在2 m处成功点亮了60 W灯泡[1],开辟了无线电能传输的新方向。目前谐振式无线电能传输尚处于探索阶段,取得了一定研究成果,主要集中在传输距离、效率、功率的提高,以及一些特殊场合(可移动设备供电)应用[2-7]上。对于系统接收端负载问题研究较少:文献[7]对系统多倍负载的功率、效率进行了研究;文献[8]研究了无线电能传输系统的负载特性,比较了感性、容性、阻性负载对系统传输效率和功率的影响;文献[9]推导了在不同距离上为抑制频率分裂现象所需的最小负载值。
本文应用集总参数理论对无线电能传输系统进行建模,推导了最大功率负载表达式,得到了与传输距离、耦合系数、系统频率等参数的关系,并通过仿真与实验证明了理论的正确性,为不同负载条件下优化系统参数提供了参考。
1 理论分析
基于两线圈结构的无线电能传输系统等效模型,如图1所示,设系统角频率为ω,Us为功率源,Rs为其内阻,L1、L2为发射和接收线圈,R1、R2为线圈内阻,C1、C2为串联谐振电容,M为互感,RL为负载。
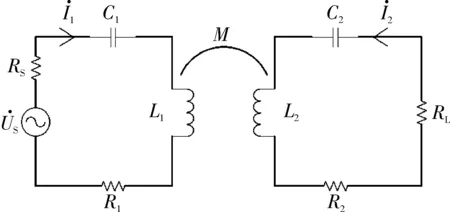
图1 无线电能传输系统等效模型
图1所示两回路KVL方程为:
(1)
式中:
(2)
系统总效率η可分为原边回路传输效率η1与副边回路传输效率η2。在两线圈发生谐振情况下,η1、η2可表示为:
(3)
其中Req为副边映射到原边的电阻,
(4)
则系统总效率为
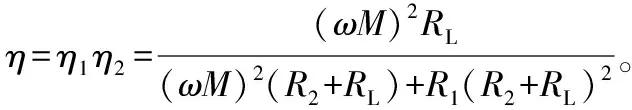
(5)
负载端的功率为
(6)
因而,在电路元件参数不变,系统运行参数(M、ω)改变的条件下,合理选择负载可获得最大功率输出。
2 最大功率负载研究
2.1 最大功率负载与传输距离关系
(7)
因而特定的负载取值将对应某一最大功率值,此时的RLPmax即为最大功率负载。
参数相同的发射线圈与接收线圈同轴放置时,其互感[10]近似为
(8)
式中:μ0为真空磁导率;r为线圈半径;n为线圈匝数;d为传输距离。由于线圈的欧姆损耗电阻通常较小,忽略损耗电阻R1、R2,对最大功率负载RLPmax的计算精度影响,所以RLPmax简化为
(9)
式中ω为线圈谐振时的角频率。可见,最大功率负载随着传输距离d的增大而减小。
2.2 最大功率负载与耦合系数关系
两线圈同轴放置时,系统耦合系数κ为
(10)
由式 (8)、(10)可得
(11)
再将式(11)代入式(9)可得
(12)
可见,耦合系数κ随着最大功率负载RLPmax的增大而增大。
2.3 最大功率负载与系统频率关系
设系统谐振频率为f0,对应角频率为ω0。当系统失谐时,副边总阻抗为
(13)

综上可得,最大功率负载在系统谐振点处达到最大,在工作频率偏离谐振频率点时减小。
3 仿真与实验分析
为验证理论的正确性,通过数值计算和电路仿真进行了实验研究,并搭建了无线电能传输实验装置,如图2所示。系统由信号发生器(Agilent 33220A)、供电直流源(Rigol DP832)、线性功放、发射与接收线圈以及可调负载组成。功率放大部分是由2个IRF530组成的甲乙类推挽式功放,其电路原理如图3所示,频率范围为5~10 MHz,最大输出功率40 W。发射线圈和接收线圈端参数如表1。

图2 无线电能传输实验装置

图3 功率放大器电路原理

参数发射线圈接收线圈半径 r/mm7575电感 L/μH1414匝数 n66串联电容 C/pf4747
3.1 最大功率负载对传输距离影响实验
接收回路负载为0~10 kΩ可调,信号源提供500 mV、6.2 MHz正弦波,供电直流源输出为12 V/1.2 A。信号经功率放大器放大后输送给发射线圈,传送至接收端。传输距离为8 cm时,理论计算最大功率负载为86.8 Ω,实验中调整电位器阻值为110 Ω时,接收到最大功率9.3 W,传输效率为52%。传输距离为10 cm时,理论计算值为40 Ω,实际测得负载为60 Ω时,获得5.6 W最大功率,传输效率为65%。传输距离为10 cm时,发射端与负载端电压如图4所示。部分实验数据如表2—3所示。
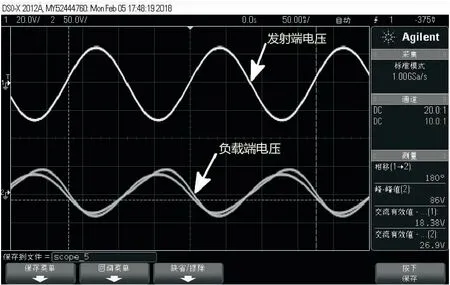
图4 d=10 cm时发射端与负载端电压

负载值/Ω电流有效值/A电压有效值/V负载功率/W800.3124.67.61100.2932.09.31500.1928.55.42000.1325.33.2
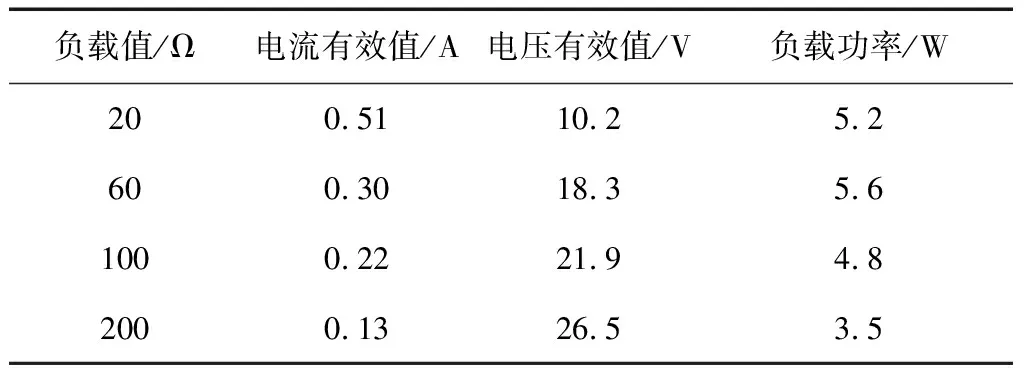
表3 d=10 cm处部分实验数据
实验测得传输距离在6~13 cm范围内最大功率负载的变化情况,如图5所示。
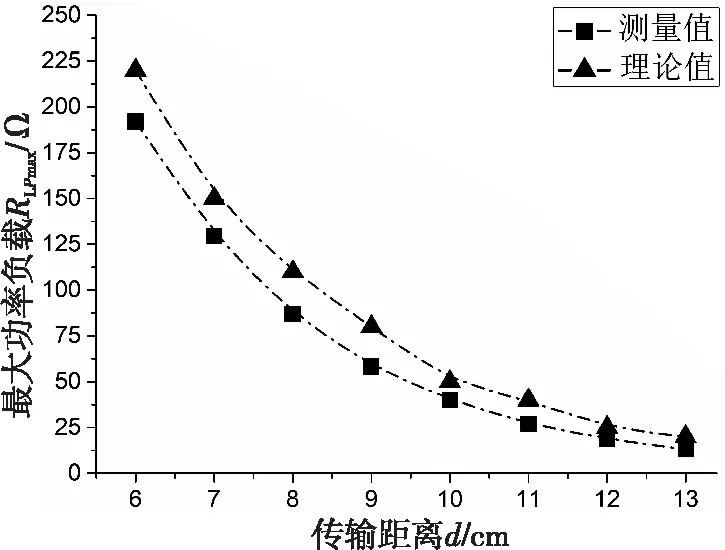
图5 传输距离与最大功率负载关系
由实验分析结果可知,最大功率负载随着传输距离的增大而减小,理论计算值与测量值基本吻合,趋势一致,最大误差小于2%。在最大功率负载所对应的传输距离上,系统将有最大功率的能量传输。当负载较小时,可以适当增加两线圈间距,以获得更大功率;负载较大时,应减小间距。
产生实验误差的主要原因是: 1)发射与接收两线圈均为手工绕制,其匝间距以及形状无法保证完全一致; 2)理论计算与实际实验中均忽略了线圈内阻和电路寄生参数;3)实际测量的误差。实验中可以设计更低的谐振频率,以便减少线圈匝数,从而减小线圈内阻及寄生电容的影响,以减小实验误差。
在传输距离大于10 cm时,理论值与测量值较接近,误差较小;传输距离小于10 cm时,误差增大。这是由于距离越近,两同轴线圈间出现频率分裂现象,影响系统的传输功率[11],进而对负载上获得的功率产生影响,导致较大实验误差。实验中可以通过在负载端增加L型阻抗匹配网络,调节系统参数等方法[12-13]来抑制频率分裂,减小实验误差。
由于传输距离和负载大小都对系统传输效率有着较大影响,因此实验中分别测试了30、40和60 Ω负载条件下,系统传输效率随传输距离的变化关系,实验结果如图6所示。

图6 不同负载下传输效率随距离的变化关系
由图6可以看出:30 Ω负载在d=14 cm处有最佳传输效率,为69%;40 Ω负载在d=12 cm处有最佳传输效率,为76%;60 Ω负载在d=10 cm处有最佳传输效率,为65%;系统传输效率随着传输距离的增加先增大后减小,存在一个最佳传输距离使系统的传输效率达到最大,且不同的负载对应着不同的最佳传输距离。因而,可以依据不同的负载设定合理的传输距离,使系统达到最佳传输效率。
3.2 最大功率负载对耦合系数影响仿真分析
为验证最大功率负载与耦合系数关系的正确性,基于Pspice对电路进行了仿真。电路结构如图7所示。功率源提供3 V(有效值)、6.2 MHz(谐振频率点)信号,发送、接收端电路元件参数如表4所示。

图7 无线电能传输电路结构

参数发射线圈接收线圈L/μH1414C/pF4747
设定耦合系数κ在0.1~0.9范围内变化,研究分析不同阻值负载上获得的功率情况。当κ为0.1时,负载在50 Ω处获得最大0.1 W功率;κ为0.5时,负载在1.5 kΩ处获得最大0.15 W功率;κ为0.9时,负载在5 kΩ处获得最大0.23 W功率。理论与仿真分析结果如图8所示,耦合系数κ随最大功率负载的增大而增大,理论计算值与仿真值基本吻合,趋势一致,最大误差小于1%。
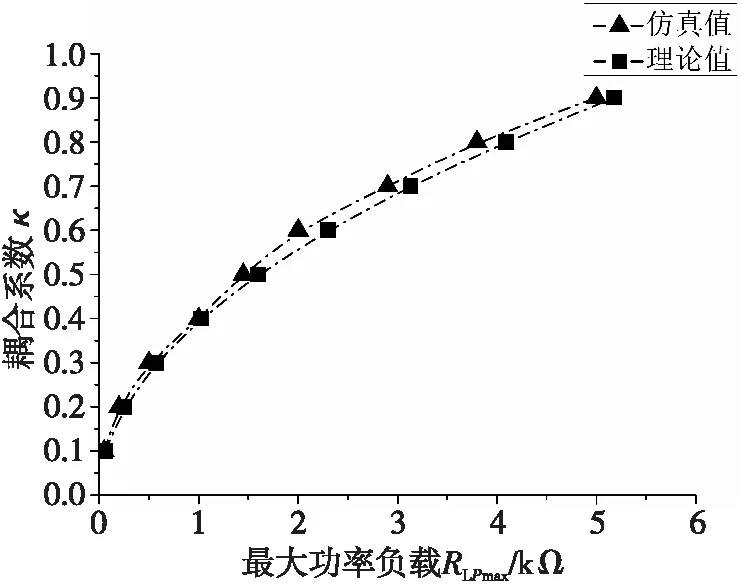
图8 耦合系数与最大功率负载关系
由上述分析可知,在最大功率负载对应的耦合系数上,系统将传输最大功率。当负载较大时,应增强两线圈耦合,来获取更大功率;负载较小时,须减小其耦合程度。
3.3 最大功率负载与系统频率关系仿真分析
采用图7中电路结构,设置耦合系数0.5,改变工作频率,在以谐振频率(5.5 MHz)为中心的正负1 MHz范围内,对不同阻值负载进行研究分析。部分仿真数据如表5所示。工作频率为5 MHz时,600 Ω负载上获得最大0.05 W的功率;在工作频率5.5 MHz处,负载1.5 kΩ上获得最大0.1 W的功率;工作频率增加到6 MHz时,最大功率负载为700 Ω,获得0.04 W功率。仿真所得频率与最大功率负载关系如图9所示。

表5 部分仿真数据

图9 频率与最大功率负载关系
由图9可见,最大功率负载RLPmax在频率为5.5 MHz处达到最大,在频率偏离5.5 MHz(谐振频率点)时减小,仿真计算结果与2.3节理论分析结论一致。
综上可知,为保证系统有最大功率传输,当工作频率接近系统谐振频率时,应选取阻值更大的负载;工作频率偏离谐振频率时,则应选取更小负载。
4 结论
本文基于集总参数理论,对磁耦合无线电能传输模型进行建模分析,推导了最大功率负载表达式,分析了最大功率负载与耦合系数、传输距离、系统频率等参数之间的关系。由仿真及实验结果可知,最大功率负载与以上参数有着一一对应关系。系统最佳耦合系数随最大功率负载的增大而增大,最佳传输距离随其增大而减小;最大功率负载在系统谐振点处达到最大,在工作频率偏离谐振频率点时减小。在实际的MCR-WPT系统中,可根据不同负载,设定与之对应的最佳传输距离和频率,保证电能的最大传输。

