半主动悬架控制策略及两种控制方法仿真

李 勋，韩寿松，郭 浩

(陆军装甲兵学院，北京 100072)

0 前言

车辆悬架系统是现代车辆中非常重要的一部分，直接影响着汽车行驶过程中的安全性、稳定性和舒适性[1]。但是目前广泛使用的被动悬架系统只能被动的跟踪外界信号，难以满足车辆在不同路况下的行驶需要。除此之外，现有悬架系统的各项性能指标互相矛盾，很难找到其最优参数组合。而半主动悬架可以通过控制，针对外界不同信号做出适当的调整，满足车辆在不同路况下的形式需要。

1 最优控制策略

最优控制策略主要有三种控制方式，分别为线性二次型最优控制(LQG)、随机线性最优控制(LQR)和 H∞控制[5]。其基本思想是根据控制目标的要求列出性能泛函，采用变分理论获得使性能泛函取极小值时的最优控制量。因此针对被控对象建立相应的数学模型是最优控制策略分析的首要工作。

在随机线性最优控制(LQG)是在线性二次型最优控制(LQR)的基础上考虑系统随机噪声与测量噪声，增加了卡尔曼滤波器所形成的控制方式。Zareh利用最优控制策略控制器计算得到车辆悬架系统的理论阻尼，随后通过建立神经网络逆模型得到磁流变减振器的通电电压，最终利用传感器测量出车辆悬架系统的状态反馈和减振器压缩速度并分别输入到控制器和减振器逆模型中构建起LQG控制策略(如图1所示)。并搭建了11自由度的整车模型来仿真分析。

图1 半主动悬架LQG控制

H∞控制是将性能指标列为无穷范数的形式,具有很强的抗干扰能力鲁棒性，但是求解过程较为复杂。帝国理工学院的Haiping Du在研究磁流变半主动悬架时采用了H∞控制 (如图2所示)，采用了减震器的位移量以及簧载质量的垂直速度作为H∞控制的输入量[6]。Fallah同样针对磁流变减振器的麦弗逊悬架系统设计了H∞控制器，并采用线性不等式进行求解，最终使用遗传算法来优化最优反馈矩阵。我国重庆大学的郑玲在研究七自由度整车模型时也采用了H∞控制，并取得了非常好的控制效果。

图2 半主动悬架H∞控制

2 应用LQR控制

应用最优控制理论的基本步骤[4]为：

1) 建立被控对象状态方程

2) 列出性能指标

3) 求解最优反馈矩阵

4) 建立仿真模型

获得最优控制问题解的过程往往较为繁琐，但如果是针对现象被控系统且性能指标是二次型的最优控制问题，则该问题的求解过程就相对容易，此类控制方法被称为线性二次型最优控制(Linear Quadratic Regulator)，简称LQ 或 LQR，该控制方法只适用于线性系统[2]。

2.1 建立被控对象状态方程

应用最优控制理论首先要建立被控对象的状态方程。对于有n个状态量、m个控制量和l个输出量的线性系统，其标准形式的状态方程可表示为：

其中，x(t)∈Rn，u(t)∈Rm，y(t)∈Rl，A(t)、B(t)、C(t)分别为，n×n，n×m，l×n，为系统矩阵、增益矩阵和输出矩阵，0l≤m≤n。

2.2 列出性能指标

性能指标J(u)以泛函的形式表示：

其中，误差向量为：

e(u)=Jr(u)-J(u).

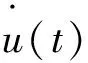
2.3 求解最优反馈矩阵

如果系统是时不变系统，且tf无限大，则性能指标中的各个矩阵都是常数，这种状态调节器称为无限时间状态调节器。

为使系统稳定，悬架系统应当在任何情况下处于可控状态。此时，使性能指标J(u)取得极小时的最优控制向量为：

其中，

K=R-1BTP.

P通过如下黎卡提(Riccati)方程求出：

ATP+PA-PBR-1BTP+Q=0.

定义z为簧载质量质心位置在车身坐标系中的坐标：zt为非簧载质量质心位置在车轮坐标系中的坐标：zr为路面高度在大地坐标系中的坐标。控制目标的选取状态量为：

因此：

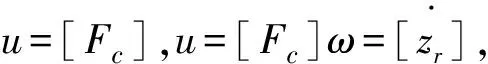
其中，

同时通过计算还可得：

无限时间的状态调节器问题可以采用Matlab中的lqr(A，B，Q，R，N)函数来进行求解。该函数求得的最优控制量为：

u*=-Kx.

K=R-1(BTP+N).

P通过如下方程求出：

ATP+PA-(PB+N)R-1(BTP+NT)+Q=0.

2.4 建立仿真模型

将随机白噪声序列作为输入，根据矩阵形式的微分方程搭建相应的Simulink模型：

K来自Matlab中的lqr(A，B，Q，R，N)函数，得出K=[5 052 -1 690 -3 018 1 425]，仿真时间为20 s，得出时域的动态曲线如图4所示。

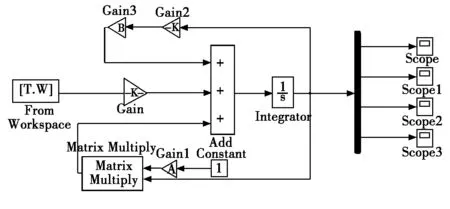
图3 Simulink仿真模型

图4 悬架动挠度仿真结果

由表1可知，利用LQR控制，可以有效提高悬架动行程，有利于提高车辆驾驶性能。

表1 仿真的均方根值

3 应用LQG控制

3.1 LQG运算原理

利用线性二次最优控制理论对1/4车辆模型进行LQG控制器的设计[3]。LQG控制的步骤与LQR控制的步骤类似，不同在于输入量为高斯白噪声序列，而非随机白噪声序列。状态空间方程为：

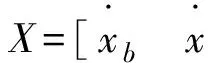
ATP+PA-(PB+N)R-1(BTP+NT)+Q=0.

得到：

K=[711.88 -1 241.5 -19 284 -2 038.5 20 864].

3.2 Matlab仿真模型的建立

Matlab仿真模型建立后将仿真时间设定为20 s，获得车身垂直加速度、悬架动行程和轮胎动位移的仿真曲线如图5，图6所示。

图5 车身垂直加速度仿真结果

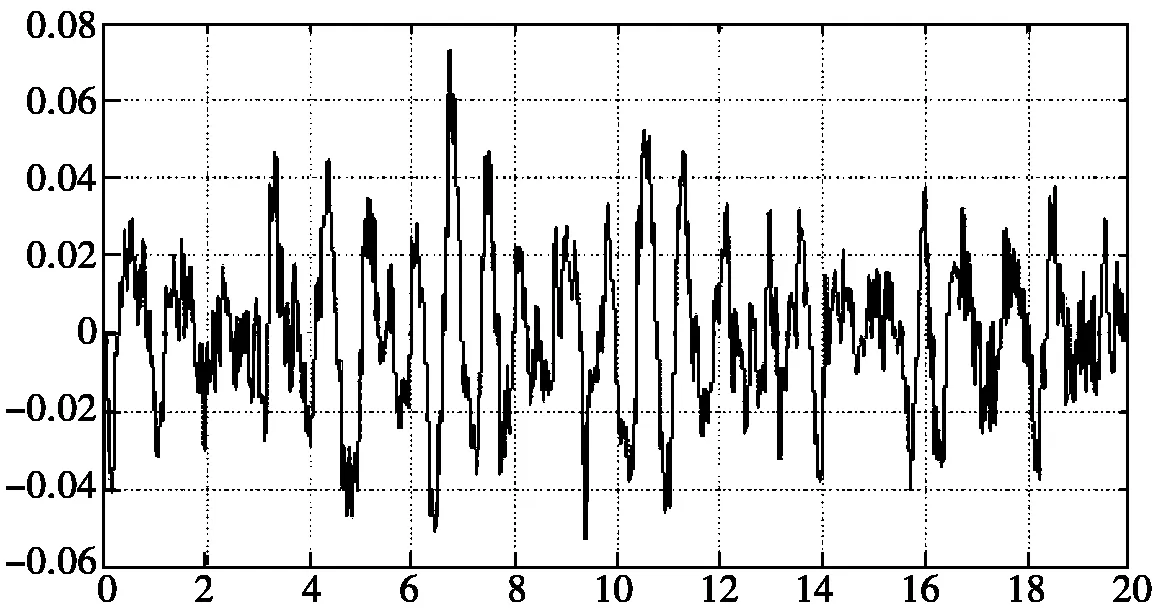
图6 悬架动行程仿真结果

由表2可知，最优主动悬架能够降低车辆行驶过程车身的垂直加速度，同时悬架的动行程也在设计所容许的范围(±100 mm)内，车辆的悬架性能得到了充分发挥。

表2 仿真的均方根值

4 总结

采用半主动悬架控制可以充分发挥车辆悬架性能。同时，通过对比LQR控制和LQG控制可以发现，LQG控制下的车辆悬架垂直加速度更小，因此可提供的车辆驾驶性能得到提高。虽然LQG控制下的悬架动行程较LQR控制有所增长，但是依旧在悬架设计所容许的范围内且两者差别不大。综上所示，LQR控制和LQG控制下的车辆悬架性能都有所提高，但是LQG控制具有更好的控制性能。