中国西北半干旱区净初级生产力驱动因子空间计算分析
姬盼盼,高敏华,*,付晓红,王鹏飞,平 渊,杨晓东,4
1 新疆大学资源与环境科学学院,乌鲁木齐 830046 2 新疆大学绿洲生态教育部重点实验室,乌鲁木齐 830046 3 新疆大学数学与系统科学学院,乌鲁木齐 830046 4 自治区智慧城市与环境建模重点实验室,乌鲁木齐 830046
净初级生产力 (Net Primary Productivity, NPP),是单位时间与单位面积中绿色植物光合作用产生的有机物质总量减去自养呼吸所消耗后的剩余部分[1,2]。NPP能够较为直接地表现生态环境表观变化和生态系统生产能力,并且能够作为环境气候变化在地球物理和生物地球化学过程中的体现[3,4]。所以,开展NPP研究具有较高的自然科学价值与社会意义。且自然环境脆弱性表达与生态效益评价等研究都与NPP有较强的关联性,它已成为环境变化过程研究和生态系统安全领域中的一个重要因子[5- 7]。NPP环境因子分析研究,在近年成为生态环境变化研究领域的热点问题,研究内容及成果包括:以NPP为监测对象的全球气候变化下地球物理与生物地球化学地表观测研究[8],借助NPP数据追踪碳循环过程研究[9],生态环境变化下的生态安全评估与预测[10],以及农田发展与质量监督的农用地NPP研究等[11]。目前,有关我国干旱与半干旱区NPP环境因子分析的研究较少,西北干旱区生态景观丰富利于获得较为客观的因子分析结果。
西北干旱与半干旱区大体呈现为高海拔山地到傍山面状绿洲,再到存在明显边界的沙漠地带景观格局。该区域地形复杂,生态景观丰富,水资源分布不均,属于生态环境脆弱区域和气候变化敏感区域,独特的自然环境条件,使得西北干旱与半干旱区成为景观生态研究的一个重要研究区[12]。另外,其环境管理与生态系统控制对区域经济发展和社会发展也具有十分重要的意义[13]。所以,对该区域内NPP环境因子响应机制进行分析,可将区域内环境变化与生态系统生产力间信息流的内在关系突显,有助于掌握该区域内生态系统生产力发展变化趋势,对区域科学持续发展及生态环境建设具有十分重要的意义与价值[14]。
目前,应用于生态环境因子分析研究的统计分析方法主要包括:主成分分析法、线性模型拟合法、马尔科夫预测、神经网络预测等方法。这些数理分析方法能够反映各因子间的数值变化关系,但并不能很好地体现对象的空间属性与地域分异特征[15- 19]。不同的生态系统有不同的地理环境设定与空间分布状态,所以在做数值统计分析时也应反映其空间属性,特别是生态环境变化研究等对于区位变化较为敏感的研究领域[20]。基于此,本文希望寻求一种带有空间属性的因子分析过程,发现因子间更多的空间关系纽带与信息流传递,为NPP生态环境变化研究解决新问题、开拓新思路,并体现空间属性在因子分析研究中的重要价值。
1 研究区概况

图1 研究区Fig.1 Study area
本研究选取新疆伊犁河谷部分区域为研究区,伊犁河谷位于中国天山山脉西部,三面环山,地处80°09′—84°56′E,42°14′—44°50′N。北与博尔塔拉蒙古自治州接壤,东与塔城地区和巴音郭楞蒙古自治州毗邻,南与阿克苏地区拜城和温宿县连接,西与哈萨克斯坦共和国交界,是古丝绸之路的北道要冲,地域优势十分突出。伊犁河谷气候温和湿润,温带大陆性气候,年平均气温约10.4 ℃,年日照时数约2870 h。全区大部分区域年均降水量350 mm左右,部分山区可达600 mm,是新疆最湿润的地区,属半干旱区。天然草场总面积约2000多万公顷,森林面积180万公顷,森林覆盖率16%,动植物种类丰富[21]。
2 方法
2.1 数据准备与整理
本研究使用中国科学院资源环境科学数据中心(http://www.resdc.cn)多年NPP监测数据、中国气象背景空间插值数据、土壤类型空间分类数据、海拔高程数据和NDVI数据,数据类型为数值型栅格数据,由数据中心网站下载后使用ArcMAP10.0软件经过空间坐标系和投影方式的统一后进行数据提取与分析工作。
2.2 数值提取
具体数据数值提取方法为:先建立一个点阵(86 Km×87 Km)形式的点属性图层,点间距离1 Km以适应原始数据的空间分辨率,确保每个点在数值提取过程中都能获得有效值。随后使用ArcGIS中Toolbox内的数值提取工具,使用之前所建立的点图层提取栅格数据中各点位像元属性值,从而获得本研究所要使用的数据集。本数据集以空间位置顺序排列导出的,即以ArcGIS的默认导出方式,从矩形点阵的左下角自左向右、自下而上依次导出空间各点位数值信息[22]。分析过程涉及因子包括年均净初级生产力(NPP,gC/m2/yr)、年均温度(tadem,缩放倍数10,℃)、年均降水(pa,缩放倍数10,mm)、湿润指数(im,缩放倍数100)、干燥指数(arid,缩放倍数1000)、大于10 ℃积温(aat10,缩放倍数10)、海拔高程(dem,m)和归一化植被指数(NDVI)。
2.3 空间分析
为能通过一些数学处理方式获得数据数值间空间关系与属性,本文使用一种全新的运算过程,获得相应具有数据空间属性和代表性的新数据集,具体运算过程为:首先,使用ArcGIS中导出的按原顺序排列的数据集,使用Matlab语言编程,将各元素转化为以空间相对位置排列的矩阵,从矩阵中选取临近的9个点作为一个新的数组,计算该数组的标准偏差(SD)、均值(Mean)和变异系数(C.V=SD/Mean),将C.V值赋值于中心点像素,计算得出C.V矩阵。空间分析相关计算使用自行编写的Matlab语言程序在MatlabR2012a(7.14)软件中计算完成,计算过程示意图见图2(a1代表像元所在点位的原数据值,cv1代表使用a1、a2、a3、a6、a7、a8、a11、a12和a13组成的小组,经过计算得到的中心点C.V值。以后的cv2、cv3等计算依次类推。):

图2 空间C.V计算过程示意图Fig.2 Diagram of the C.V calculation process
2.4 统计分析
如果只通过本文计算的C.V数据集做后续数理统计分析,得出的结果无法与前人研究相互验证,所以本文首先使用常规数据处理方式将原数据做相关分析和回归分析获得主要驱动因子,随后使用本文提出的带有空间关系的C.V数据集来完成相应的分析与处理,从而证明本研究方法的可行性与科学性,并对比分析两数据集间的联系与差异。
3 结果
3.1 原数据C.V处理
使用Matlab软件和86 Km×87 Km矩形样方中提取的属性数据,完成空间C.V统计分析得到以各因子相对空间位置重建的C.V影像,各因子经过Matlab软件计算和可视化处理后结果见图3:图3中结果可发现积温(>10 ℃)、温度和干燥度的C.V在空间分布上存在明显的关联与相似性,降水、湿润指数相关性强,这也一定程度上验证了本实验数据处理方法的稳定与可靠性。获得影像结果后,将影像内各像元属性值重新提取出来获得C.V数据集,本研究将使用新的C.V数据集与原始数据集同时做统计分析,对比分析两数据集因子分析结果,探索本研究中使用的空间统计分析(本文认为可称之为空间邻域变异系数法,C.V计算)方法在因子分析中运用的可行性与科学性。另e和f图中条带是由于与原数据在做空间插值处理时,图像拼接处留下了未能全局处理的边界插值误差带。
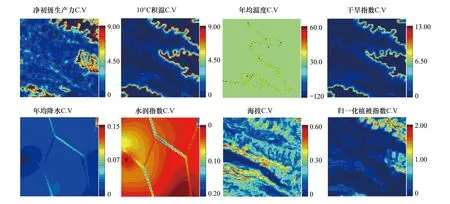
图3 C.V计算影像化处理Fig.3 C.V calculation image processing
3.2 数据集因子相关分析
随后,本研究还需对C.V数据集做更为深入地统计分析和处理,从而突显一般数理统计分析处理与本文空间统计分析在分析结果中差异性。
原数据集做相关性分析(图4)发现相关性极强(|R|>0.9)的是:aat10—tadem、tadem—dem、aat10—dem。该结果是可以预见的,因为积温可以由温度计算得出,温度受海拔的升高而随之降低,当然积温也就随之降低,这三个因子两两相关。其中,与NPP有较强相关性的是温度与海拔。

图4 原始数据集因子相关性Fig.4 Factors correlation of Normal datasets***表示相关极显著
为探寻原始数据集因子相关性与C.V数据集间存在的差异,本文对C.V数据集做了相关性分析。为能更为详细地表达温度降水两大主要因子与NPP的相关性,对其做空间相关性分析,结果如图5:由图5可知降水与NPP在研究区的大部分区域呈正相关,而温度则存在相对较多的负相关关系。且此处正负相关分界线基本与山脊线重合,地形变化对此有显著的主导力。

图5 NPP-温度-降水空间相关性Fig.5 NPP-Temperature-Precipitation spatial correlation
C.V数据集相关性分析结果中(图6)有极强相关性的是paCV—imCV和ariCV—aat10CV,其中湿润指数可由年均降水计算得出,环境积温可影响蒸发量。与NPPCV有较强相关性的是年均降水、湿润指数、海拔和归一化植被覆盖指数(NDVI)。不难发现C.V数据集中能让更多因子与NPP因子间的相关性得以体现出来,而且降低了环境各因子间的相关性,更能客观地体现因子间的真实关系。
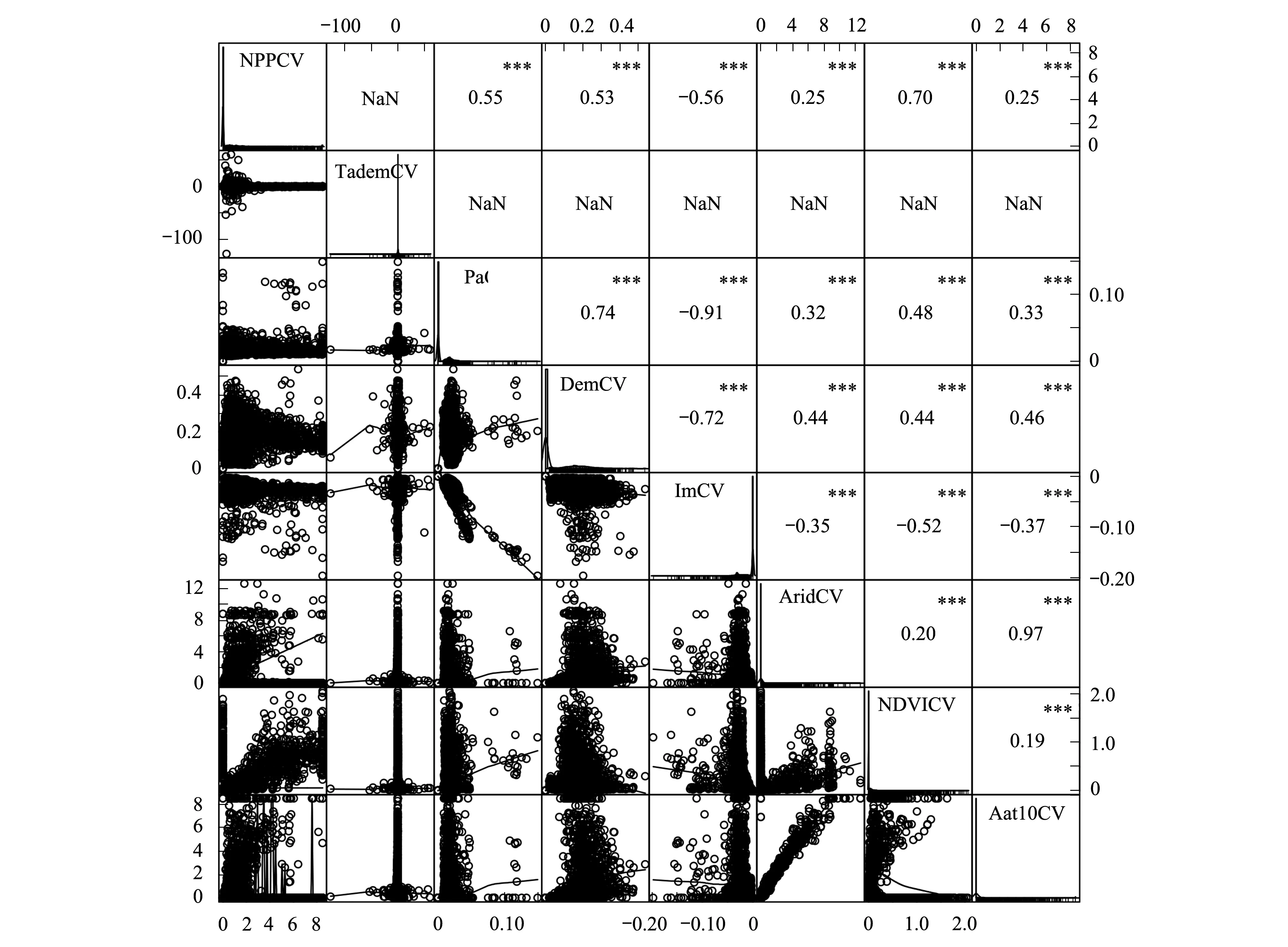
图6 C.V数据集因子相关性Fig.6 Factors correlation of C.V datasets
3.3 NPP环境因子建模
各环境因子与NPP间的数值变化关系和贡献度需通过模型拟合和预测等方法分析获得,因此,本文分别以NPP和NPPCV为因变量,其他因子为自变量做逐步回归分析,结果见表1。
逐步回归方法优势在于,能对因变量有较高主导能力的因子做出筛选与排序,使得该结果可直观地表达各自变量因子在模型构建中的重要性。由表1发现,各因子对于NPP的重要性排序,在两个数据集间存在差异,最显著的差异表现在第二因子,原数据集中为积温,而C.V数据集为海拔,且积温在C.V数据集中未被选为重要因子,海拔在原数据集中也未被选为重要因子。且使用两数据集拟合获得的线性模型中,C.V数据集拟合度明显高于原数据集,说明C.V数据集拟合模型的解释能力更强,体现出的因变量变化趋势更准确,也肯定了C.V计算在因子分析研究中应用的可行性。
3.4 C.V数据集因子海拔分布
在以往其他研究区域中,其NPP因子分析结果中海拔因子并没有成为NPP的主要驱动因子,可知干旱区海拔因子对NPP作用能力较强,所以本文试图以海拔为尺度划分,使用C.V数据集做Duncan分析,分类结果如图7:经方差分析发现(图7)除年均气温C.V值在海拔尺度上未能体现出较显著的差异外,其余因子均可分为4—6组,在海拔尺度下存在显著的差异性,这也验证了海拔因子对NPP以及其他环境因子的重要性。

表1 原始数据集与C.V数据集回归分析
y:净初级生产力,net primary productivity;Xndvi:归一化植被指数,Normalized difference vegetation index;Xaat10;大于10 ℃积温,>10 ℃Accumulated temperature;Xarid:干燥度,Aridity;Xpa:降水,Precipitation;Xim:湿润指数,Humid index;Xtadem:高程校正年均温度,Average annual temperature (elevation corrected);Xdem:海拔,Elevation
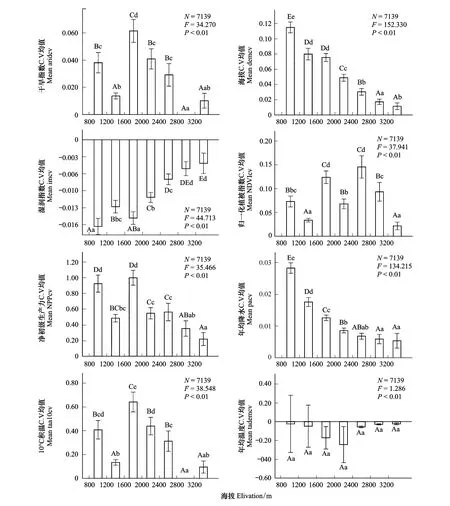
图7 C.V因子海拔尺度Duncan显著性检验Fig.7 Duncan significance test of C.V factor at altitude scale
4 讨论
生态特征要素的环境因子分析研究一直是生态系统演变与模拟研究中最为基础与核心的内容,通过量化因子间协同变化关系和空间区位关系,寻求具有较高稳定性和科学价值的数学模型或预测模式,可以帮助人们更加科学地监测和管理生态系统[23- 25]。本研究通过引入C.V计算过程,期于将因子间的空间关系得以量化和表达,从而探索其在因子分析中的可行性与实际价值。因子相关性分析和回归分析结果均可体现C.V计算在因子分析中的价值,验证了该研究方法在大尺度分析研究中应用的可行性与科学性。各因子C.V计算分析结果以图像展现,可以直观地反映出该因子相应空间位置的波动变化强度,也可认为是变化频率在邻域空间内的记录。其计算过程选择相邻9个邻近像元为一个小组参与计算,结果值赋值于中心点位像元,所以,C.V计算结果表达了因子在拓扑空间的数值变化强度,也就是中心点周围的紊乱程度或稳定程度[26,27]。这种计算削弱了计算小组以外因子的干扰,使该方法能更加灵敏地洞察变化的存在,对因子变化的响应更敏锐。
相关性分析主要反映因子间的关联程度,是一种较为常见的探究因子间关联度的方法。本研究相关性分析结果发现:原始数据集中,相关系数r值较高的两因子在C.V数据集结果中也相对较高,两结果十分相像。但也有个别因子间的r值存在较大差异,例如NPP—tadem两因子(R=0.50),在C.V数据集结果中R值偏小(R=-0.03)。经初步分析认为, C.V计算使得两因子关联度减弱的原因是:C.V计算的本质是将空间小邻域间的波动关系突显出来,但同时又相当于对原始数据做了归一化处理,使之成为无量纲的参数,而就原始数据数值本身的大小分布无较高的敏感性,所以分析时建议两者结合使用能较全面的说明问题[28]。由此可知,C.V计算能较好地表现因子空间波动变化关系7,而对于数值分布变化并不敏感。
两数据集拟合模型因子重要性排序,第一因子均为NDVI,原因是NDVI作为地表植被生长状态信息的直接表达因子NPP的内在联系较强,且NPP是年内单位面积上有机物积累量减去消耗损失量计算获得。所以植被盖度能间接影响该地域有机物的净产量,而消耗量差异较小时,NDVI因子对NPP的驱动能力将得到加强[29,30]。原数据集第二因子为大于10 ℃积温,积温作为温度和能量供给的另一种体现,对植物体的生命活动有十分重要的作用,植物可简单分为喜温与喜凉作物,但适宜生长的环境温度都在零度以上[31,32],所以积温达到一定数值时,植被才能较为充分地完成自身代谢与能量积累,而且在干旱区积温的高低变化对地表水分蒸散活动影响也十分明显,进而能间接影响植物体水力提升活动和对各器官的水分供给能力[33,34]。C.V数据集第二因子为海拔,说明海拔的变化在小邻域范围内对NPP的作用效果是十分显著的,海拔变化能直接影响区域降水条件和环境温度等诸多自然环境因素,进而作用于土壤属性和植被分布等生态环境因子,这是地理与环境学者们所公认的,沙漠地区的绿洲均“依山而立”就是很好的例证[35]。
在以往的研究中没有提出海拔因子对NPP的显著作用力[36],本研究通过均方差分析发现C.V在海拔尺度下存在显著差异,说明各因子在不同海拔范围内的变化具有区域特点,再次肯定了海拔对半干旱区环境下NPP的重要性与分化作用。各因子中除经过DEM校正的年均气温没有显著地分组效应,其余各因子都表现出了显著地组间差异(P<0.01)。另外,不难发现C.V数据集在模型拟合中结果更优,模型更稳定。在模型的建立过程中,一般认为SEE越小模型越好,更具说服力,但我们知道当因子数量增多时,随着变量自由度的增大,SEE便会减少。所以这时我们需要注意调整R2的变化,即当变量增多,实现了SEE减小,R增大,如果调整R2也随之变大则说明我们加入的变量对因变量是有意义的,相反调整R2减小或不变则说明新加入的因子是不必要的。当然,更少的变量获得更高的R值,是最为理想的模型构建目标。根据该原理,结合本研究中获得的结果,可说明使用C.V数据集获得的NPP多元线性模型更优。且原始数据集模型R值最大为0.654,而C.V数据集R值最小为0.697,肯定了C.V计算数据处理过程在多元回归分析中运用的前景与科学性。依据上述因子筛选理论与分析结果,表明本研究所选择的因子对NPP多元线性模型的建立均具有显著统计学意义,且具有一定的科学性。
5 结论
本文通过矩阵计算重建数据空间相对位置,完成地图软件无法直接实现的空间分析过程,经地理空间数据处理方法的创新与改进,最终完成对原数据添加空间属性的计算过程,且新数据集在因子分析中表现出良好的应用价值与科学性。依原数据集和C.V数据集统计分析与处理结果,我们可以得出以下结论:
(1)在干旱区环境下环境因子中NDVI、积温和海拔对NPP的作用相对较强(P<0.01),具体表现为积温对植被生长的积极推动作用与海拔对温度和局部降水条件的控制。
(2)C.V空间统计计算处理后的数据集在耦合分析中有一定的模型拟合优势(P<0.01),且与未经处理的数据集相比能使一些隐性因子突显出来。
(3)C.V空间统计计算影像化处理,能将数据中特定因子邻域变化强烈的空间区域,更直观,更精确的表达,使因子空间浮动变化特征一目了然。
(4)与原数据集相比C.V数据集拟合获得的模型拟合度更高,具有较强的说服力(P<0.01)。
(5)各因子的C.V值分布在海拔尺度上存在显著的分布差异(P<0.01)。
致谢:感谢中国科学院地理科学与资源研究所资源环境数据中心(http://www.resdc.cn)为本研究提供原始数据与相关技术支持,感谢平渊与王鹏飞同学在程序编写中给予的帮助。

