非正交多址下行链路的资源分配与仿真
李 泽
(南安普顿大学 电子及计算机学院, 南安普顿 SO17 1BJ, 英国)
非正交多址(Non-Orthogonal Multiple Access,NOMA)技术[1]的用户分配研究分为上行链路和下行链路两种,上行链路的用户分配研究主要集中在编码域,下行链路的用户分配研究集中在功率域。
非正交多址技术下行链路的基本思想是,在发送端采用多载波技术,在功率域使每个子载波服务于多个用户,在接收端采用串行干扰消除技术(Successive Interference Cancelation,SIC)来消除复用用户之间的相互干扰。文献[2]比较了非正交多址下行链路与正交频分复用下行链路的系统容量和频谱效率。文献[3]介绍了构建非正交多址下行链路仿真平台的方法,并通过该平台分析小区内的用户数量对非正交多址系统表现的影响。文献[4]证明了即使在高速传播数据的情况下,非正交多址系统也可以产生很高的功率增益。
在子载波与用户功率分配研究方面,文献[5]研究了两个用户共享一个子载波的情况。文献[6]提出了一个子载波服务两个以上用户的方案,共享同一子载波的用户之间依靠各自从基站获得的功率进行区分,并使用串行干扰消除技术进行解调;由于一个子载波可以服务两个以上用户,共享同一子载波的几个用户之间会产生复用增益,系统具有更高的频谱效率。文献[7]详细阐述了串行干扰技术在非正交多址下行链路中的解调过程。文献[8-9]的用户分配方案中,每个子载波可以根据其信道空闲情况服务不同数量的用户,使用户分配方案变得更加灵活高效,子载波的利用变得更加合理。
以上关于非正交多址下行系统用户配对以及功率分配的研究中,没有过多考虑用户的安全性。本文提出基于稀疏码映射的非正交多址下行链路用户分配模型,在这种模型中,从基站获得的功率较弱的用户可以在不降低系统频谱效率的前提下,获得更公平的信道功率增益,并在此分配模型的基础上对不同用户分配方案的系统性能进行探究和仿真。
1 系统模型及基本参数
非正交多址下行链路模型中,基站发出的信号可以表示为:
(1)
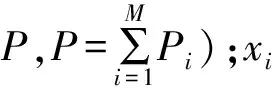
假设在接收端用户i接收到的信号为y(i),则:
yi=hixi+wi
(2)
式中:hi表示用户i的信道;wi表示表示用户i的噪声。
非正交多址下行链路在解调时采用串行干扰消除技术。当一个基站服务两个用户(用户1和用户2)时,其信道容量可以分别表示为[5]:
(3)
(4)
式中:h1、h2表示用户1和用户2的信道;P1、P2表示用户1和用户2从基站得到的功率;N0表示噪声的功率密度。
以此类推,对于有M个用户的下行链路,总的信道容量可以表示为:
(5)
此外,影响非正交多址系统的重要因素还有传播时遇到的大尺度衰落[10]和小尺度衰落。大尺度衰落是由于传播时的路径损耗和阴影所引起的,大尺度衰落的概率密度函数[10]如下:
(6)
式中:β表示大尺度衰落;λ=10/ln10;μ(d)表示10lgβ2的方差;σβ表示10lgβ2的标准差;d表示基站与用户之间的距离;μ(d)定义如下:
(7)
式中:d0表示参考距离,通常在100~300之间;α表示路径损耗指数,范围通常在3~5之间[11]。
小尺度衰落又称为多径衰落,子载波数为N的非正交多址系统,其小尺度衰落由下面公式得出:
(8)
式中:hi表示用户i的信道;F表示快速傅里叶矩阵;φL表示长度为N的单位矩阵的前L列;L表示模拟小尺度衰落中滤波器的系数,文中设L=6。
传统的多用户非正交多址下行链路模型[11]如图1所示。在此模型中,假设系统共有4个子载波,每个子载波服务两个用户,由于串行干扰消除技术的影响,解调时共享同一个子载波的两个用户,距离基站较远的用户会把自己的全部信息暴露给离基站较近的用户,这种情况对边缘用户十分不公平,有着严重的安全隐患。
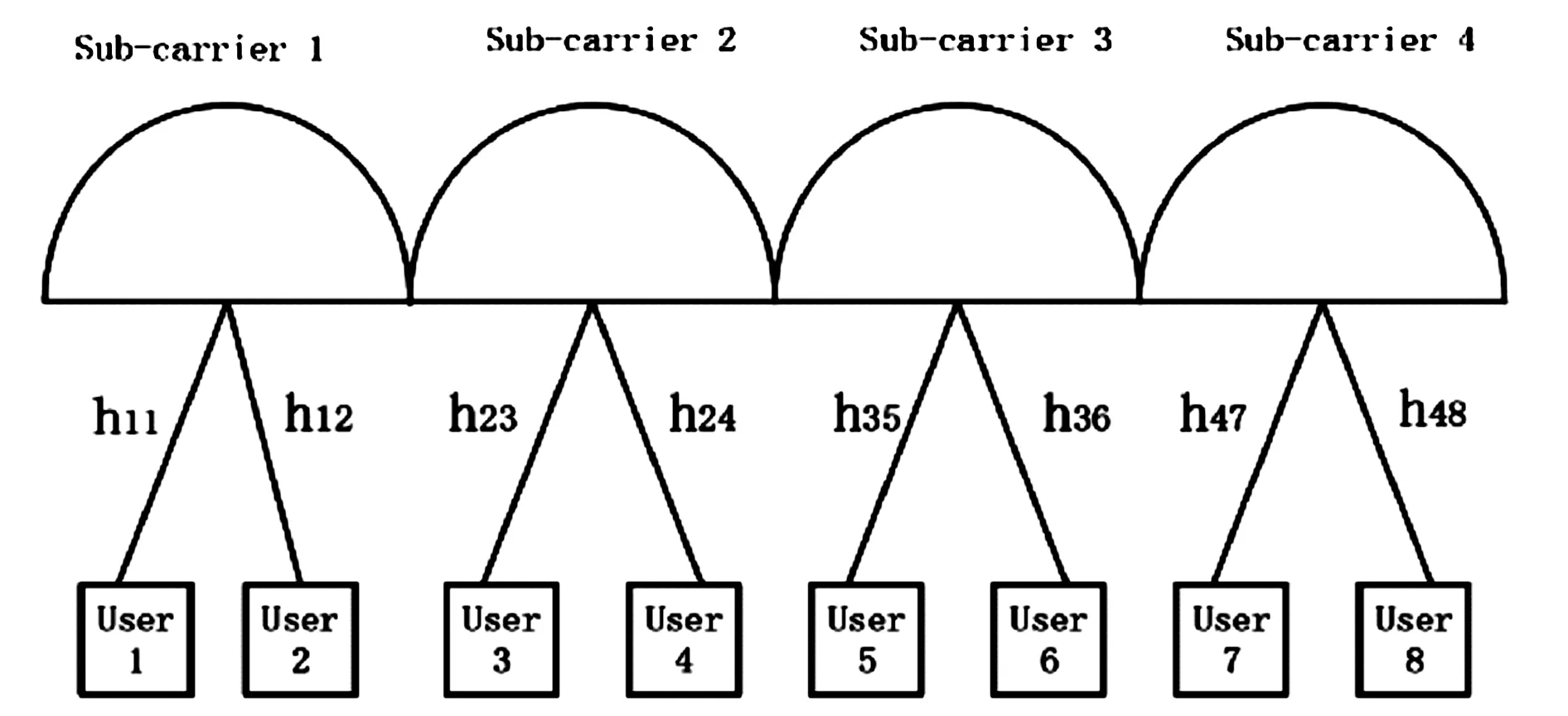
图1 传统的多用户非正交多址下行链路模型
本文提出一个基于稀疏码映射的非正交多址下行链路模型(见图2)。在此模型中,两个用户共享同一子载波,同时多个子载波也服务于同一个用户。每个子载波只包含其服务的用户的部分信息,从而在进行解调时,同一个子载波服务的两个用户中,距离基站较近的用户只可获取距离基站较远的用户的部分信息,保护了用户隐私,提高了安全性。
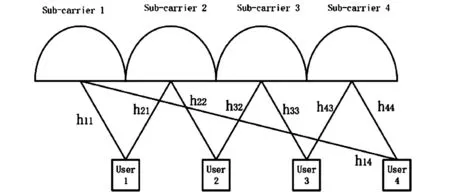
图2 基于稀疏码映射的多用户非正交多址下行链路模型
在图2所示的模型中,假设有N个子载波,每个子载波服务dm个用户,其中dm≥1,同时需要给每个用户分配dn个子载波,则系统中用户的总数量M可以表示为:
(9)
在此模型下,串行干扰消除技术应用于共享同一子载波的用户之间而非全部用户之间。对于使用稀疏码映射模型传递的信号,其全部用户和子载波的信道增益矩阵为:
(10)
Gmn表示用户m在第n个子载波上受大尺度衰落以及小尺度衰落影响的信道功率增益(m=1,2,…,M;n=1,2,…,N),其中每一行代表一个用户在所有子载波下的信道功率增益。为了满足基于稀疏码映射的模型,需要从矩阵G中每一行取出dn个元素,从每一列中取出dm个元素。为了更加方便地选取元素,本文引入通常用于非正交多址上行链路中的稀疏码映射法,具体过程如下:
第一步,构造一个N×N的单位矩阵I,单位矩阵I的第n列代表第n个子载波的映射位置。
第二步,构造一个M×N的全部元素为零的矩阵A。
第三步,用户1,2,…,M需依次从矩阵I中取出dn列,并且每一列只能被选择dm次。


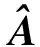
在基于稀疏码映射的非正交多址下行链路中,用户k从子载波l处获得的解调信号为:
(11)
频谱效率是用来衡量系统容量的重要指标,文中的频谱效率用系统的归一化传输速率(Sum-Rate)表示,其单位为:(bits/s)/sc,其中sc表示子载波的数量。在基于疏松码映射的多用户非正交多址下行链路模型中,用户k在子载波l上的频谱效率可以表示为:
(12)
式中:l=1,2,…,N;k=1,2,…,M;Wl表示共用子载波l的全部用户的集合;σ2代表标准正态分布的方差。
要得到整个系统的频谱效率,需要将所有用户在每个子载波上的频谱效率叠加:
(13)
这里,需要分别考虑每个子载波上的频谱效率,子载波的频谱效率可以表示为:
(14)
式中:Qk表示用户k上的全部信道能量增益,包括大尺度衰落增益和小尺度衰落增益。
所以,整个系统的频谱效率也可表示为:
(15)
2 用户配对方案
本文主要介绍了3种基于疏松码映射的多用户非正交多址下行链路模型的子载波-用户配对方案。
第一种方案是随机分配[9],在这个方案里,用户在服从式(9)的前提下,被随机分配给各个子载波。设定子载波数量为24,改变系统中的用户数量(24,36,48),系统频谱效率的变化如图3所示。
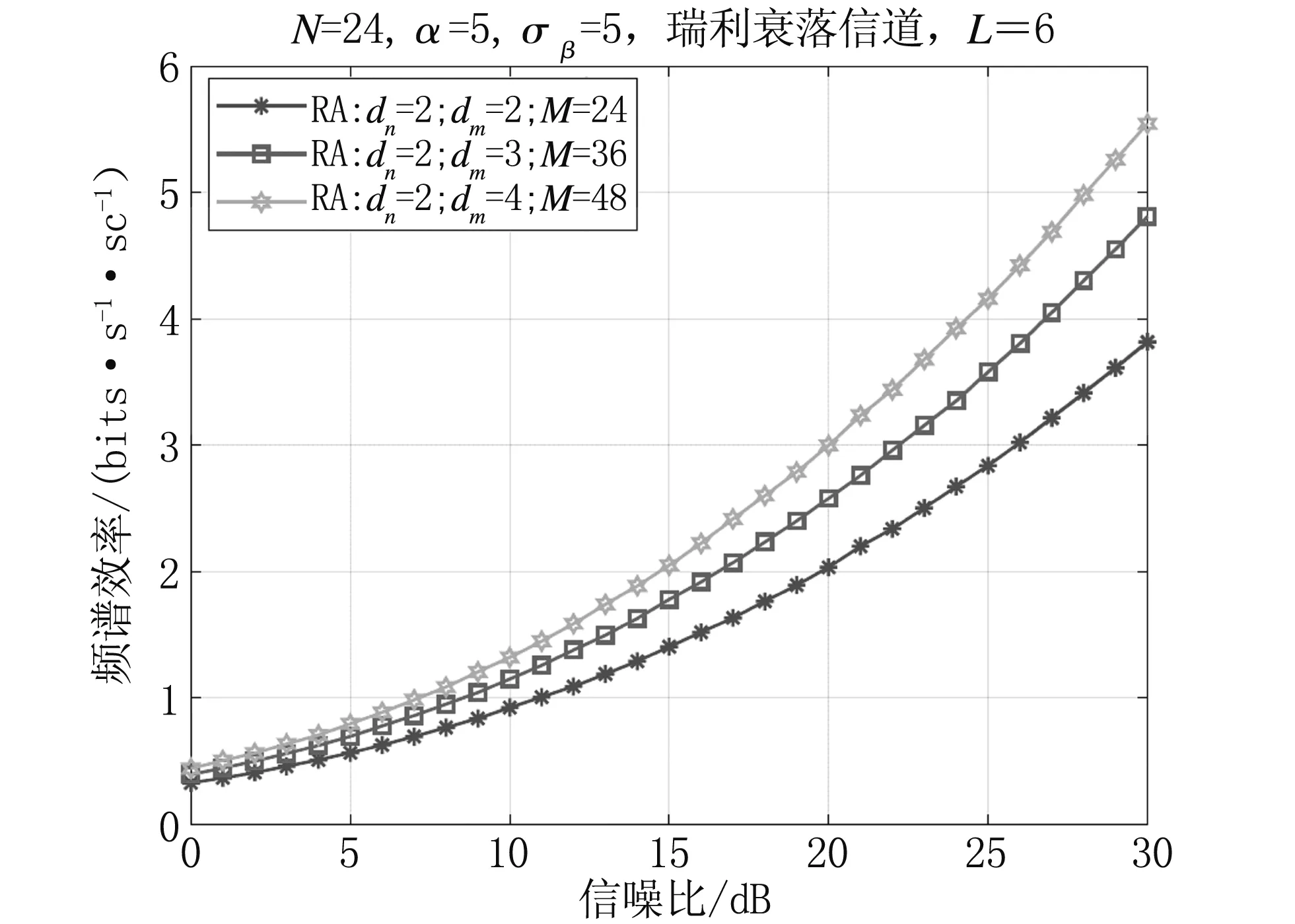
图3 随机用户分配方案中用户数量对系统频谱效率的影响
从图3可以观察到,在其他参数都固定的情况下,随着系统中用户数量的增加,系统的频谱效率也在不断增加,这些增益是由用户之间的复用增益产生的。

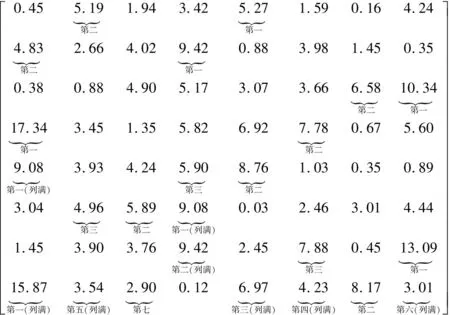
(16)
用户1从第一行中选出信道功率增益第一和第二大的子载波,即一行5列和一行2列,并标记其位置。用户2~4的操作与用户1相同,分别选出自己所在行中信道功率增益第一和第二大的子载波。观察发现,从用户5开始,其信道功率增益最大的子载波所在列已经被选择2次,所以用户5需要放弃该子载波,选择信道功率增益第二、第三大的子载波。可以观察到,到用户8,子载波基本都被选满,所以其选择的余地不大,只能选择信道功率增益第二大以及第七大的子载波。
通过以上贪婪算法选择,可以得到下列子载波分配矩阵:
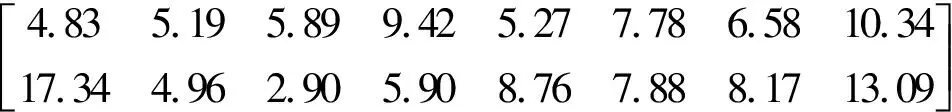
(17)
再根据用户及子载波的具体配对情况带入式(15),即可获得该系统的频谱效率。
基于贪婪算法的分配方案,需要获取所有用户的信道状态信息,运算量较大,运算时间较长,但其优点是可以选出相对合适的用户分配方案。
3 仿真结果及分析
本文基于MATLAB 2018b平台进行了仿真。在仿真中设定N=24,dn=2,dm=3,α=5,σβ=10,L=6,信道均为瑞利衰落信道,信噪比为:0~30(dB),每个数据点循环105次,并且所有系统的总功率均设为1个单位能量。
图4是3种用户分配方案的频谱效率仿真结果。从图中可以观察到,随着信噪比的提高,3种用户配对方案的频谱效率都在不断提高。相较于随机用户分配方案,基于大尺度衰落的用户分配方案有较高的系统频谱效率,并且复杂度较低,具有较高的实际意义。相较于其他两种用户分配方案,基于贪婪法则的用户分配方案明显具有更高的频谱效率,但此方案需要获取更多的用户信道状态信息,复杂度较高,实现起来需要更长的运算时间。在今后的研究中,如果贪婪算法的运算过程能得到优化,则基于贪婪法则的用户分配方案可更好地运用于实际通信系统中。
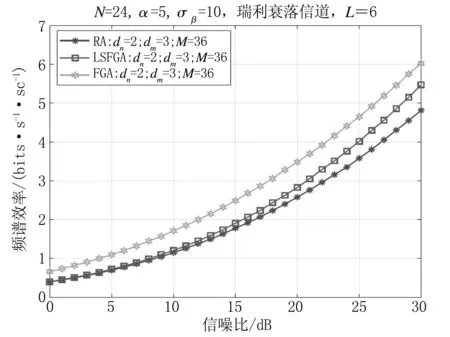
图4 3种用户分配方案的频谱效率对比
在使用同一种用户配对方案时,通过实验探究路径损耗指数对系统频谱效率的影响。固定参数N=24,dn=2,dm=3,L=6且通过瑞利衰落信道,改变路径损耗指数(α=4,5,6)。仿真结果如图5所示(基于大尺度衰落的用户分配方案)。
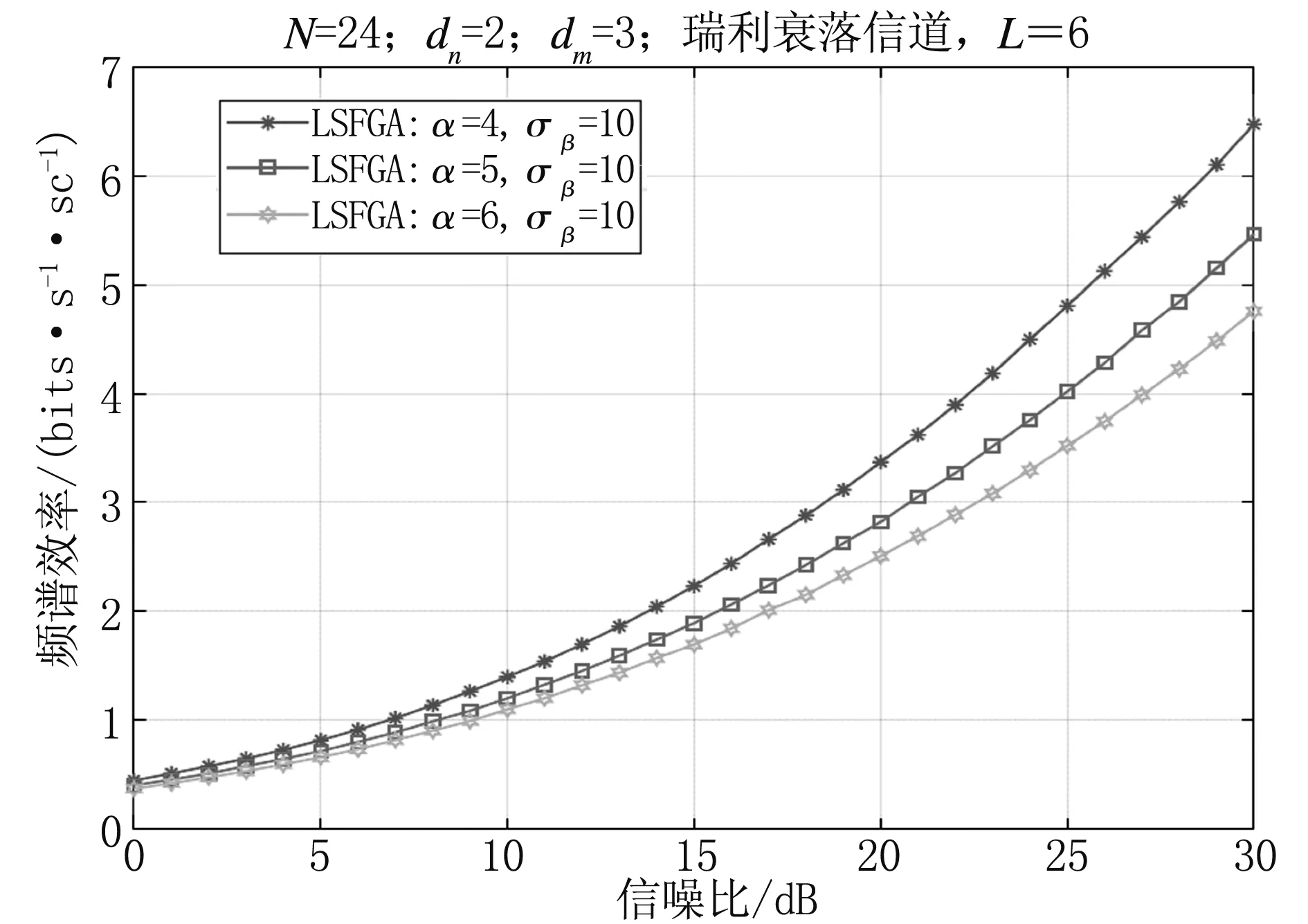
图5 路径损耗指数对系统频谱效率的影响
由图5可知,在其他参数固定的情况下,随着路径损耗指数的提高,系统的频谱效率不断下降。这是由于信号在传播过程中,随着路径损耗指数的提高,信号的损耗越来越严重。针对随机用户分配方案和基于贪婪算法的用户分配方案的仿真得到了相同的结果,所以对于非正交多址下行链路,信号传播时路径损耗指数越大,系统的频谱效率越低[13]。
4 结 语
传统的非正交多址下行链路对于边缘用户有很大的安全隐患,本文提出的基于稀疏码映射的非正交多址下行链路模型能较好地解决这个问题。文中提出了3种用户-子载波分配方案并对其进行了仿真,仿真结果表明,在其他实验条件都相同的情况下,基于贪婪法则的用户分配方案具有最高的频谱效率,但同时也具有最高的复杂度,目前不宜在通信系统中直接应用。基于大尺度衰落的用户分配方案可以有效提高系统频谱效率,且复杂度较低,易于实现。另外,在使用同一种分配方案时,系统的路径损耗指数越大,其传输过程中能量损失越大,频谱效率越低。

