不同林龄长白落叶松人工林林分结构研究

栗生枝

(辽宁省林业调查规划监测院，辽宁 沈阳 110122)

林分结构是指在未遭受严重干扰、经过长期的自然生长、枯损与演替的情况下，林分内许多特征因子，如直径、树高、形数、材积、树冠等都具有一定的分布状态，而且表现出较为稳定的林分结构规律[1]。林分结构内含着这些反映林分特征因子的变化规律，探讨这些规律对森林经营技术、编制经营数表及林分调查都具有重要意义。

随着林业科技进步及统计分析科学的发展，林分结构模型朝着复杂化、多样化方向发展，从而从整体上提升了林分结构模拟与预测系统的性能及准确度，更能为科学营林和准确预估材积提供翔实的数字依据。

在林分内各种大小直径林木按径阶的分配状态，称作林分直径结构(Stand diameter structure)，亦称林分直径分布(Stand diameter distribution)。在林分中，不同树高的林木按树高组的分配状态，称作林分树高结构(Stand height structure)，亦称林分树高分布(Stand height distribution)[2]。林分直径结构和林分树高结构都是最基本、最重要的林分结构，将直接影响树木因子的变化。因此研究同龄纯林的直径及树高结构规律在营林技术方面具有重要的指导意义。

1 试验地概况

西丰县郜家店镇位于铁岭东北部，距县城22 km。郜家店镇属中温带亚湿润区大陆性季风气候，四季分明，气候温和，雨量充沛。年平均气温5.1 ℃。1月平均气温-17 ℃，最低气温-41.0 ℃；7月平均气温23.2 ℃，最高气温35.2 ℃。年平均降水量738 mm， 无霜期135 d，土层厚度50 cm左右，腐殖质层厚3 cm左右。

试验地、对照地全部为人工落叶松纯林，林相整齐，易于作业，便于管理。

2 研究方法

2.1 固定样地设置

在西丰县郜家店镇林区选择坡度平缓、有代表性的长白落叶松(Larixolgensis)人工林，分不同林龄(18年生、22年生、38年生)设置样地，样地面积25 m×25 m。共设样地132块。其中18年生林分设置样地36块，22年生林分设置样地48块，38年生林分设置样地48块，样地概况见表1。

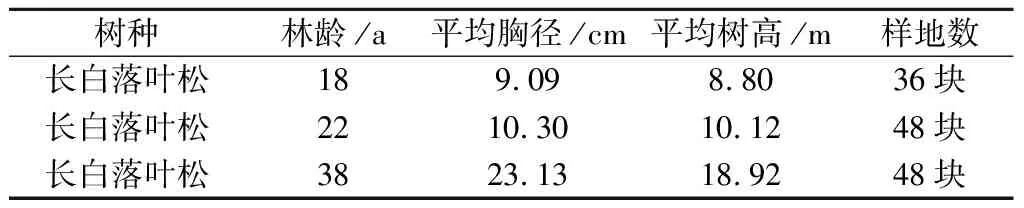
表1 样地概况

2.2数据搜集

在标准地内对所有乔木进行每木检尺，详细记录每株树的胸径、树高、冠幅、枝下高等林木因子以及坡度、坡向、海拔等立地因子。并按胸径2 cm为一个径阶，树高为1 m为树高距分组记录数据。

2.3 分析方法

2.3.1 正态分布法

(1)正态分布概率密度：标准正态分布的概率密度为：

(1)

m——林木实测直径/树高值；

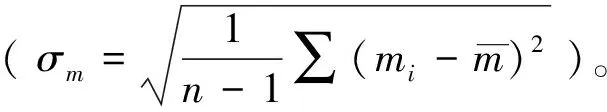
(2)

在正态分布中，以数学期望及方差为分布参数，只要林分算术平均直径(树高)及标准差计算出来之后，然后借助已有的正态分布函数表计算出林分直径正态分布中各径阶株数理论值。最终与实测株数对比结果进行卡方检验，研究拟合效果。

2.3.2 卡方检验 林分株数按径阶和树高分布的现实结构需进行卡方检验才能确定是否真正符合拟合曲线。

设x= (x1,x2,…xn) 为长白落叶松林分各径阶(树高)实际株数所构成的数列，y= (y1,y2…yn) 为利用拟合曲线分布得到长白落叶松林分各径阶(树高)理论株数所构成的数列。则χ2统计量为：

3 结果与分析

3.1 长白落叶松林分直径结构

根据径阶中值及其对应株数值绘制直径分布曲线，如图1。

由图1可以看出，3个林龄的林分直径分布曲线的具体形状虽有些差异，但都形成一条以林分平均直径为峰点、中等大小的林木株数占多数、向其两端径阶的林木株数逐渐减少的单峰山状曲线，类似服从正态分布曲线。因此，可以用正态分布对直径分布曲线进行拟合。

利用林分的算术平均直径及标准差(表2)就可以拟合出林分直径的正态分布函数，根据该函数，即可求出林分直径正态分布中各径阶株数理论值(表3)。

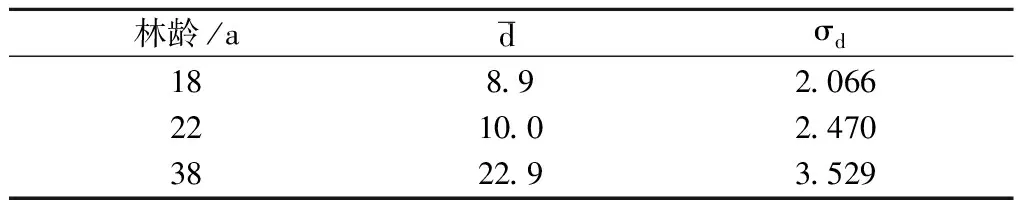
表2 各林分直径的期望和标准差值

表3 长白落叶松人工林直径分布拟合结果 株

对拟合效果进行分析及卡方检验，结果见表4。

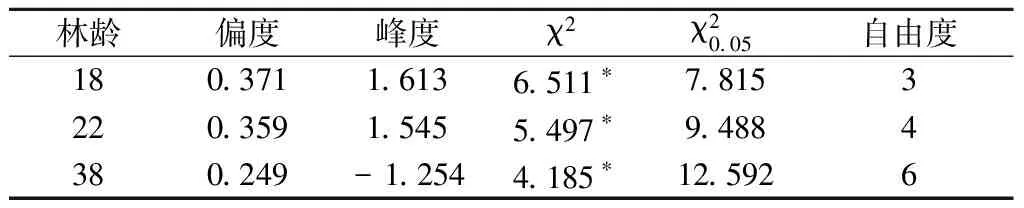
表4 长白落叶松人工林直径分布拟合效果分析

注：χ2值中带* 的为符合分布的标准地

由表4可知,3个林分的直径分布曲线均可以用正态分布很好的拟合。与相对直径法所得结果相同，18年、22年、38年生长白落叶松林分直径的偏度系数均为正值，其绝对值均分布在[0.2，0.4] 区间，说明该标准地林木直径分布为左偏。从峰度分布来看，18年、22年生林分的峰度为正值, 说明它们比正态分布曲线略为陡峭，38年生林分的峰度为负值，说明该曲线比正态分布曲线略为平坦。其中，18年生林分的直径分布曲线偏度、峰度最大，38年生林分的偏度、峰度最小，其曲线更近似于正态分布。说明随着林分林龄的增长，林分平均直径逐渐增大，直径分布曲线的峰度由大变小，形成宽而平的分布曲线，更接近于正态分布曲线。出现这种情况的原因可能是：幼龄阶段，林分密度低，光照、营养、空间充足，林木生长必须的条件都可以满足，竞争压力小，所以林木生长速率差别不大，其胸径均集中在林分平均直径左右，中等大小的林木株数占绝大多数。但随着年龄的增加，林木生长所需的空间和养分增多，而林地所能提供的空间、养分有限，林木竞争逐渐加剧，此时，林木生长速率出现差异，林木生长量大小开始分化，随着时间的推移，这种分化越来越明显，因而出现林木胸径分布分散化，即林分直径分布曲线峰度减小，形成宽而平的分布曲线。

3.2 长白落叶松林分树高结构

根据树高值及其对应株数值绘制树高分布曲线，如图2。

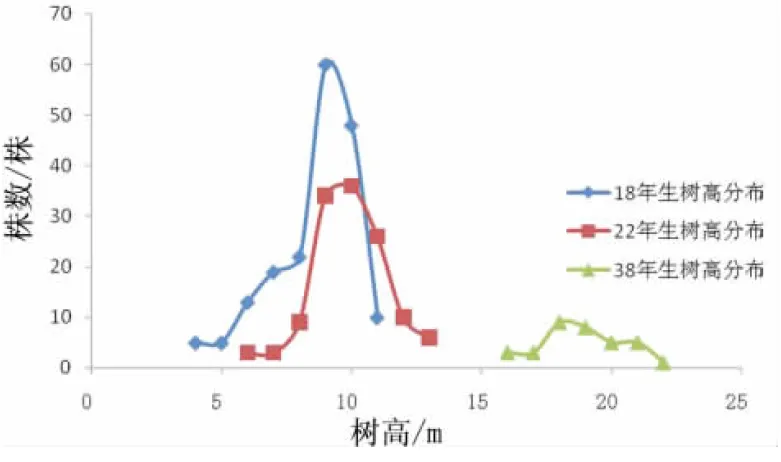
由图2分析表明，3块长白落叶松人工林的树高分布具有明显的结构及变化规律，呈现出近似于以该林分平均高的株数最多的非对称性的山状曲线。

表5 各林分树高的期望和标准差值

表6 长白落叶松林树高分布拟合结果(株)

近似服从正态分布曲线。因此，可以用正态分布对长白落叶松林树高分布曲线进行拟合。

利用林分的算术平均树高及标准差(表5)就可以拟合出林分树高的正态分布函数，根据该函数，即可求出林分树高正态分布中各径阶株数理论值(表6)。

对拟合结果进行分析和卡方检验，结果如表7。

表7 长白落叶松林树高分布拟合效果检验

注：χ2统计量值中带* 的为符合分布的标准地

依表7所示，正态分布对3个林分的树高分布曲线拟合效果非常好。3个林龄的长白落叶松林分树高的偏度系数均为正值,其绝对值分布在[0.1，0.5] 区间，说明该标准地林木树高分布为左偏，说明林分内树高中等和偏低的林木较多，而对林分直径结构的分析表明林分内中小径阶的林木占多数，胸径、树高刚好可以对应，说明3个林龄的林分内中等及偏小的树占多数。但相对树高法得出的结论是38年生林分的树高分布为右偏，可能是由于相对树高法拟合效果不理想，导致误差产生所致，应以正态分布所得结果为准。从峰度分布来看，峰度为负值, 说明它们比正态分布曲线略为平坦。与林分直径分布曲线不同的是，树高分布曲线峰度随着林分年龄的变化基本保持不变，并不随着林分年龄的变化而有明显增大或减小的趋势。这也说明，与胸径生长不同，树高生长受林分密度影响较小，其很大程度上取决于立地条件的优劣。

4 结论和讨论

根据以上分析和检验结果，得出正态分布对林分直径和树高结构的拟合效果好，灵活性大、适应性强，且随林分林龄的增大，拟合效果越来越好。根据正态分布的拟合结果得出，西丰县郜家店镇地区不同林龄的长白落叶松人工林林分直径和树高分布均为单峰左偏正态分布，即各个林龄的林分内中等及偏小的树占多数。直径和树高结构分析是林分蓄积量和出材量表编制的基础，即各径阶单株木材积乘以相应径阶株数得径阶蓄积合计，各径阶蓄积合计得林分蓄积合计；各径阶蓄积乘以相应径阶不同材种的出材率得径阶材种出材量，径阶材种出材量合计得林分材种出材量合计。因此，本研究为建立西丰县郜家店地区长白落叶松人工林收获预估体系提供一定的理论依据。

本文仅以正态分布法对样地直径树高结构进行分析，分析方法较为单一，应进一步运用相对直径法和相对树高法进行比较分析，得出更能反映西丰县郜家店地区长白落叶松人工林林分结构的方法。