一种仿人肩关节的运动学和工作空间分析
孙鹏, 李研彪, 郭明飞
(浙江工业大学 机械工程学院, 浙江 杭州 310023)
0 引言
肩部的整体运动可以分为两类:第1类是肩关节在胸廓上的运动,第2类是上臂相对肩胛骨的运动(绕3个轴的旋转运动),这两类功能区域能够各自或共同运动[1]。目前,仿人肩关节主要用于实现第2类的运动功能。
相对于串联机构,并联机构具有结构紧凑、高刚度和运动灵活等特点,使其在仿生领域具有重要的应用[2-3]。近年来,已有不少学者将球面并联机构应用于仿人领域,例如:杨龙等[4]提出的3-RRR+(S-P)人形机器人仿生肩关节,王跃灵等[5]和张亮[6]提出的基于正交球面3-RRR机构的机器人肩关节,侯雨雷等[7]提出的3-PCSS/S球面并联肩关节机构。但上述并联机构存在结构尺寸大、姿态工作空间小、加工和装配工艺性差等问题。另一方面,因为上臂的内旋、外旋运动范围小,并且是多关节的协同运动[1],所以一些学者将肩关节视为2自由度机构[8-9]。本文为紧凑仿人肩关节机构,提出基于球面5R并联机构的仿人肩关节。
机构运动学分析包括位移运动学和速度运动学,这些分析是关节空间和末端执行器空间之间的线性关系,是精确控制和运动规划的基础[10]。研究者一般用Denavit-Hartenberg(DH)表示法分析位移和速度运动学[11],但是DH方法存在一些缺陷,如奇异性问题和在速度运动学中难以表明瞬时性的物理意义。然而,基于旋量理论和指数积公式表示的刚体运动,以其简洁的数学符号和明确的几何意义而受到更多研究者的应用[12]。黄真等[13]首次系统地应用旋量理论和指数积公式对并联机构进行了分析与性能研究。另一方面,并联机构的固有奇异特性影响着机构设计、分析和控制,因此分析机构的奇异位形与结构参数之间的关系,对机构应用具有重要作用[13-14]。
并联机构的工作空间求解方法包括解析法和数值法。解析法求解工作空间精度高,但其研究过程非常复杂,依赖机构位置解的研究成果,至今仍没有完善的方法[15]。数值法通常利用运动学逆解,并考虑机构的结构参数和运动学限制,搜索得到工作空间[13]。数值法较简单,适用性较好,主要采用坐标搜索方式,精度主要取决于搜索步长[16]。在结构参数优化方面,并联机构的工作空间优化具有参数众多、参数敏感性差异大、参数间耦合强等特点,因此作为高维非线性问题,其寻优算法的设计是一个难点[17]。空间模型技术可以研究结构参数与性能指标之间的关系,但多数研究3个结构参数[18-19]。遗传基因算法非常耗时,且收敛性不确定[20]。因此对于多个结构参数与各性能指标之间的关系,需要进一步深入研究。
本文提出了一种基于球面5R并联机构的仿人肩关节,基于旋量理论和指数积公式对该并联机构建立了数学模型,并给出了这类少自由度非对称型并联机构的运动学分析方法。在运动学分析基础上确定约束条件,得到了工作空间计算方法,对比人体肩关节灵活活动区域定义了工作空间评价指标,分析了工作空间评价指标与结构参数之间的关系,同时考虑加工装配工艺最终选取了一组较合理的结构参数。
1 构型分析
1.1 结构布局
以球面5R并联机构为原型的仿人肩关节机构简图如图1所示,此并联机构由静平台、动平台和2条运动支链构成。运动链1由连杆A1B1、B1C1和动平台通过转动副连接而成,其中OA1、OB1、OC1为各转动副轴线。运动链2由连杆A2C2和动平台通过转动副连接而成,其中OA2、OC2为各转动副轴线。2条运动链的5个转动副轴线汇交于一点,称为机构中心,记为点O. 静坐标系为OXYZ,原点与机构中心点O重合,Z轴垂直于静平台,指向静平台正上方,Y轴与轴线OA2始终重合,X轴方向由右手螺旋定则确定。动坐标系为OX1Y1Z1,Z1轴与轴线OC1始终重合,指向动平台正上方,X1轴与轴线OC2始终重合,Y1轴方向由右手螺旋定则确定。初始姿态下,动坐标系与静坐标系重合,轴线OB1在平面OX1Y1上。
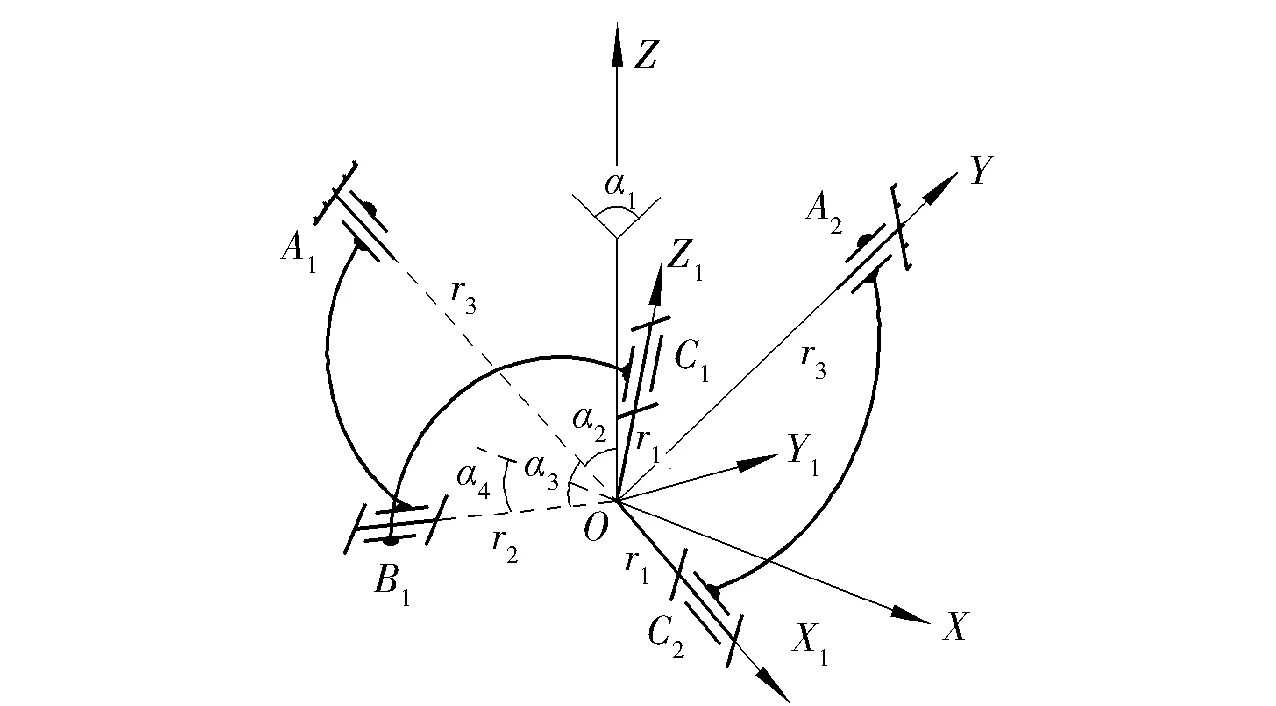
图1 仿人肩关节机构简图Fig.1 Schematic diagram of mechanism of humanoid shoulder joint
图1中:α1为平面OA1Z与平面OA2Z的夹角;α2为Z轴与轴线OA1的夹角;α3为轴线OA1与轴线OB1的夹角;r1为转动副C1、C2与机构中心点O的距离;r2为转动副B1与机构中心点O的距离;r3为转动副A1、A2与机构中心点O的距离。
同时为简便运动学运算,定义了1个中间参数α4,表示轴线OB1与平面OA1Z的夹角。根据三余弦定理,cosα3=cosα4cos (π/2-α2),故α4取值与α2和α3的取值有关。
1.2 自由度分析
采用基于约束螺旋理论修正的Grübler-Kutzbach公式[21-22],对该并联机构进行自由度分析,
(1)
式中:M表示机构自由度;d表示机构阶数;n表示包括机架的构件数;g表示运动副数;fi为第i个运动副的自由度;ν表示冗余约束数;ζ表示局部自由度。
运动链1的螺旋系为
(2)
式中:ξA1为转动副A1的运动螺旋坐标;ξB1为转动副B1的运动螺旋坐标;ξC1为转动副C1的运动螺旋坐标。
上述螺旋系为3系螺旋,当α1=α4+π/2时,该螺旋系为2系螺旋,但此时轴线OA1和OB1共面,不符合设计要求。则这个3系螺旋的反螺旋系为
(3)
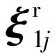
(3)式表明,运动链1约束了动平台沿动坐标系3个坐标轴方向的移动。
运动链2的螺旋系为
(4)
式中:ξA2为转动副A2的运动螺旋坐标;ξC2为转动副C2的运动螺旋坐标。
上述螺旋系为2系螺旋,则反螺旋系为
(5)

(5)式表明,运动链2约束了动平台沿动坐标系3个坐标轴方向的移动和绕Z1轴的转动。
比较2条运动链的反螺旋系(3)式和(5)式可知,2个分支有3个公共约束,则d=6-3=3. 当去掉3个公共约束后,动平台的反螺旋系仅有1个绕Z1轴的约束力偶,因此没有冗余约束,故ν=0. 通过观察,该机构没有局部自由度,则ζ=0. 因此

(6)
上述分析结果表明,该仿人肩关节机构具有2个自由度,即动平台绕动坐标系X1轴和Y1轴的2个转动自由度。此外,机构位形改变时(不包括奇异位形),(3)式和(5)式保持不变,因此机构自由度数目和性质不发生改变,从而证明了机构自由度的全周性。
2 运动学分析
2.1 位置正解
设动平台绕动坐标系X1轴、Y1轴旋转角度分别为γX1、βY1,用欧拉角(Z-Y-X)描述动平台的位姿,得到动平台的姿态矩阵[13]为

(7)
基于姿态矩阵R,轴线OC1、OC2在静坐标系中表示为
(8)
(9)
基于广义坐标系,轴线OB1、OC2在静坐标系中表示为

(10)
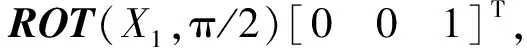
(11)
式中:θA1为转动副A1的输入角度;θA2为转动副A2的输入角度。
由该并联机构的结构特点,可以得到如下约束关系:
OC2=OC2,
(12)
OB1·OC1=0.
(13)
将(12)式整理后,得
βY1=θA2-π/2.
(14)
将(14)式代入(13)式,整理后得
γX1=arctan2(A,B),
(15)
式中:
A=cosθA1sinθA2sinα2sinα3+cosθA2sinα1sinα2cosα3+
sinθA2cosα2cosα3-sinθA1cosθA2cosα1sinα3-
cosθA1cosθA2sinα1cosα2sinα3;
B=sinθA1sinα1sinα3-cosθA1cosα1cosα2sinα3+
cosα1sinα2cosα3.
由此,该并联机构的位置正解如(14)式和(15)式所示。(14)式表明动平台绕Y1轴的旋转角βY1只由转动副A2的旋转角θA2决定,因此该并联机构具有部分解耦的特点。
2.2 位置反解
首先由旋量理论和指数积公式建立该并联机构的运动学模型,其次利用Paden-Kahan子问题思路将该运动学逆解分解为若干个具有明确几何意义的逆解子问题[23],然后逐步加以解决。
1)求解θA1,对于运动链1,建立正运动学模型:
g(θ)=exp (A1,θA1)·exp (B1,θB1)·
exp (C1,θC1)·g(0),
(16)
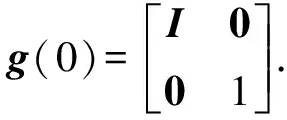
(16)式两边同右乘g-1(0),得
exp (A1,θA1)·exp(B1,θB1)·exp(C1,θC1)=
g(θ)g-1(0).
(17)
取轴线OC1上一点p1,其齐次坐标p1=[0 0 1 1]T, (17)式两边同右乘p1,得
exp(A1,θA1)·exp (B1,θB1)·p1=
g(θ)·g-1(0)p1.
(18)
根据Paden-Kahan子问题2求解(18)式,得
exp(A1,θA1)·(±c1)=q1,
(19)
式中:c1为求解过程中的已知向量,表示c1有2组解;中间变量q1=g(θ)·g-1(0)·p1.
根据Paden-Kahan子问题1求解(19)式,得

(20)
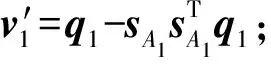
2)求解θA2,对于运动链2,建立正运动学模型:
g(θ)=exp(A2,θA2)·exp(C2,θC2)·g(0),
(21)
式中:θC2为转动副C2的转动角度。
将(21)式两边同右乘g-1(0),得
exp (A2,θA2)·exp (C2,θC2)=g(θ)g-1(0).
(22)
将(22)式两边同右乘p1,得
exp (A2,θA2)·exp (C2,θC2)·p1=
g(θ)·g-1(0)p1.
(23)
根据Paden-Kahan子问题2求解(23)式,得
exp (A2,θA2)·(±c2)=q1,
(24)
式中:c2为求解过程中的已知向量,表示c2有2组解。
根据Paden-Kahan子问题1求解(24)式,得
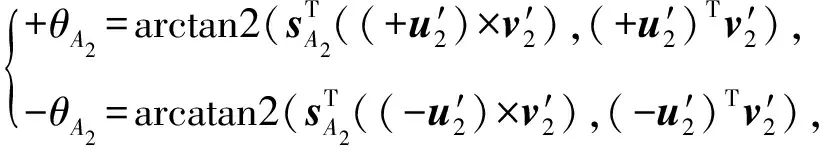
(25)
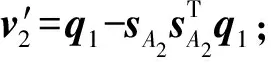
需要说明的是,在旋转运动情况下,因为在运动的旋转分量求解时,ξ和θ的选择是不唯一的,所以变换exp:se(3)SE(3)是多对一的,从而导致当给定位形处于工作空间内,会有多组关节角对应于末端执行器的同一个位置映射[21]。但对于上述并联机构,由于运动平台对2条运动链的约束作用,每条运动链的关节角只能取一组解。进而得到该并联机构的位置反解:
(26)
2.3 速度分析
这种仿人肩关节机构属于少自由度非对称并联机构类型,针对这类并联机构特点,基于旋量理论和指数积公式,结合少自由度并联机构的直接法和虚拟机构法[13,23]求解速度雅可比矩阵。
对于串联机器人速度雅可比矩阵,通过旋量理论得
(27)
ξ′i=Adξi,
(28)
式中:ξi表示第i个关节的运动旋量坐标;n表示机构关节总数。
对于该并联机构的运动链1,应用少自由度并联机构的直接法求解该运动链的雅可比矩阵:
(29)
式中:v表示动平台速度;ξ′B1、ξ′C1通过(27)式和(28)式求得。
该并联机构具有2个转动自由度,故(29)式可化简得
(30)
式中:ω表示动平台角速度;sA1、sB1、sC1表示转动副轴线的单位方向向量。
在非奇异位形,由(30)式得
(31)
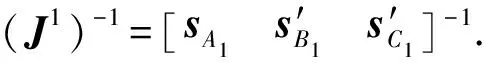
对于该并联机构的运动链2,在该分支增加虚拟的运动副D2,其运动螺旋坐标为ξD2=[0 0 1 0 0 0]T,其旋转角度、速度、加速度均为0. 应用少自由度并联机构的直接法求解该运动链的雅可比矩阵:
(32)
在非奇异位形,由(32)式得
(33)

运动链1中输入副为转动副A1,因此取(J1)-1的第1行。运动链2中输入副为转动副A2、D2,因此取(J2)-1的第1行和第3行。将上述行矢量组合,得到
(34)
在非奇异位形,由(34)式得
(35)
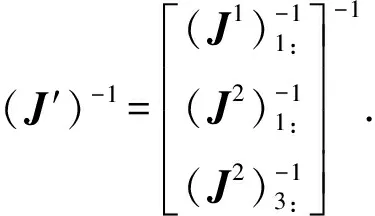
最后去掉虚拟运动副D2,(J′)-1去掉最后一列,得到该并联机构的速度雅可比矩阵:
(36)
通过分析(36)式,并代入多组机构参数验证得到
(37)
(37)式表示动平台在静坐标系中绕Y轴转动的角速度分量只与输入转动副A2的速度有关。
2.4 奇异位形分析
对于与机构性能密切相关的奇异问题,最通用的方法是分析雅可比矩阵的奇异性,当雅可比矩阵的奇异值为0时,机构处于奇异位形。但是对于并联机构,应用2.3节求雅可比矩阵方法的前提是各运动支链非奇异,这说明当各运动支链奇异时,并联机构的雅可比矩阵不存在,这也是这种方法的不足之处。另一种常用方法是线几何法,即按线几何原理,当代表运动副轴线的线性相关时,机构奇异。这种方法同上一种方法存在同样问题,当各运动支链奇异时,并联机构不一定奇异。因此,本文针对该并联机构的特点,基于判断奇异的物理学方法,将机构的其余输入锁住,仅留下1个输入,分析动平台此时的运动情况。
当并联机构位姿如图2所示时,运动链1中转动副的运动旋量坐标线性相关,轴线OA1、OB1、OC1共面。
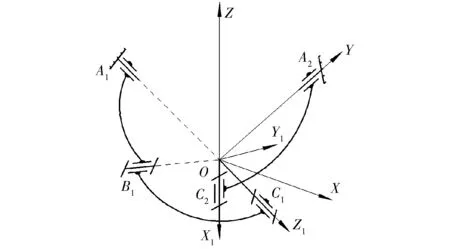
图2 奇异位形1Fig.2 Singular configuration 1
如图2所示:锁住输入转动副A2,动平台在转动副A1驱动下绕动坐标系的X1轴转动;锁住输入转动副A1,动平台在转动副A2驱动下绕动坐标系的X1轴、Y1轴转动。此时,运动链1中转动副的运动旋量坐标线性相关,但并联机构并没有处于奇异位形,从而证明了上述分析。需要说明的是,当轴线OA1、OC1共线时,该并联机构确实失去了绕动坐标系X1轴转动的自由度,但是这种情况只发生在机构参数取α1=π/2 rad,α2=π/2 rad,α3=π/2 rad时。
当并联机构的位姿如图3所示时,运动链2的反螺旋系发生变化,轴线OC1、OA2共线。
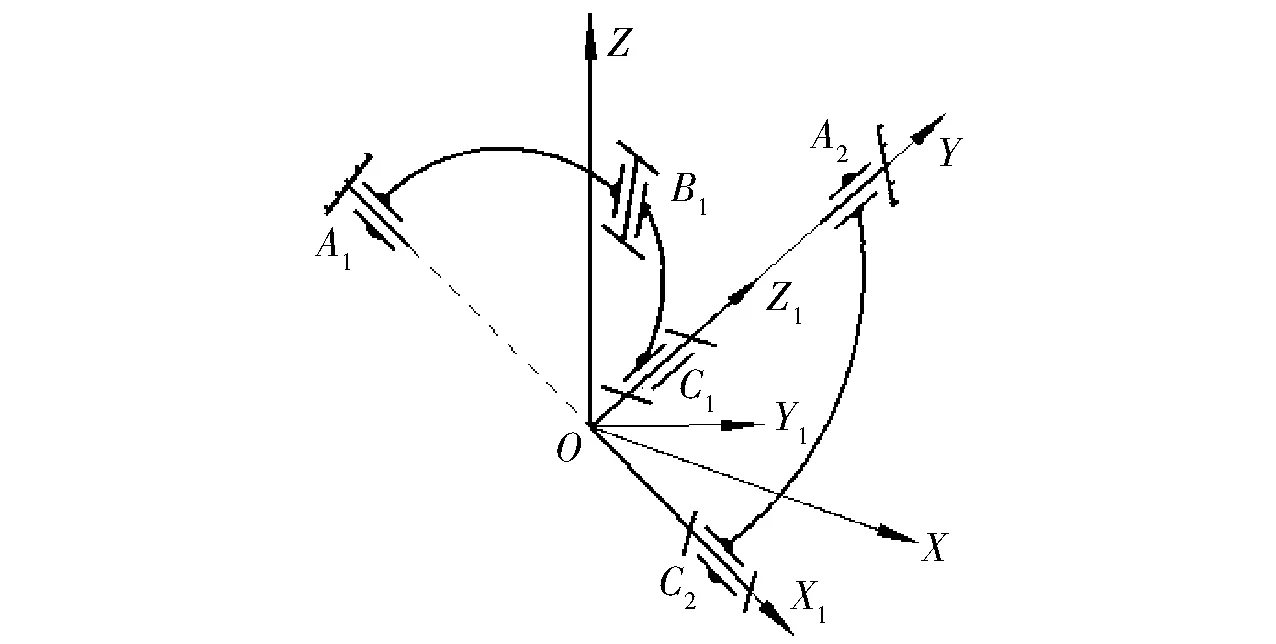
图3 奇异位形2Fig.3 Singular configuration 2
由图3可见:锁住输入转动副A2,动平台在转动副A1驱动下绕动坐标系的X1轴转动;锁住输入转动副A1,动平台在转动副A2驱动下绕动坐标系的Z1轴转动。此时,机构处于奇异位形,但仅是自由度性质发生变化,数量并没有减少。
3 工作空间分析
并联机构存在动平台绕动坐标系X1轴、Y1轴旋转的2个自由度。针对这种运动学特点,该并联机构的工作空间也可以称作姿态工作空间。建立该并联机构的三维模型,如图4所示,其初始结构参数如表1所示。

表1 初始结构参数
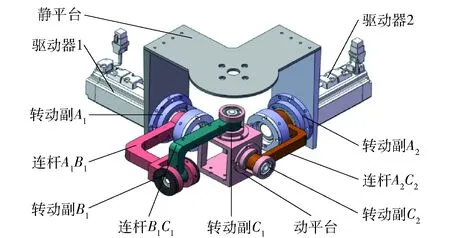
图4 仿人肩关节的结构Fig.4 Structure of humanoid shoulder joint
3.1 约束条件
根据该并联机构的结构特点建立姿态空间的约束条件,约束条件包括运动副转角约束和运动杆件干涉约束[12]。
3.1.1 运动副转角约束
如图4所示,各转动副必然不能整圈转动,当该并联机构处于初始位姿时各转动副转角为0°,转角转动正方向按照右手螺旋定则确定,则得到各转动副转角约束条件:
θkmin≤θk≤θkmax,k=A1、B1、C1、A2、C2.
3.1.2 运动杆件干涉约束
3.1.2.1 机构连杆间干涉
针对该并联机构的运动特点,只需检测杆件B1C1、A2C2之间是否发生干涉。杆件不发生干涉的条件是:两杆件的最短距离dmin不小于杆件最大截面圆的直径Dmax. 机构间干涉情况较为复杂,黄真等[13]对这类问题做了详细论述。
3.1.2.2 杆件与基座间的干涉
针对该并联机构的结构特点,需检测杆件B1C1、A2C2是否与静平台和转动副支座发生干涉。同时考虑到此并联机构将作为仿人肩关节,动平台将连接大臂样机,因此动坐标系Z1轴负方向不能与静平台发生干涉。上述干涉不发生的条件是杆件与基座的交点不在杆件和基座范围内。
3.2 求解姿态工作空间
给定动平台任意一个姿态,求得各转动副转角,满足约束条件的姿态包含在姿态工作空间内。本文采用坐标搜索法[13],搜索空间为βY1[-π rad,π rad]、γX1[-π rad,π rad]. 由于动平台具有2个转动自由度,无论动平台处于何种姿态,姿态工作空间点集[24]均在1个平面内。将平面内点集的数量作为该组结构参数下的姿态工作空间大小[25]WSV.
选取结构参数如表1所示,迭代步长取10°,该并联机构的姿态工作空间仿真结果如图5所示。
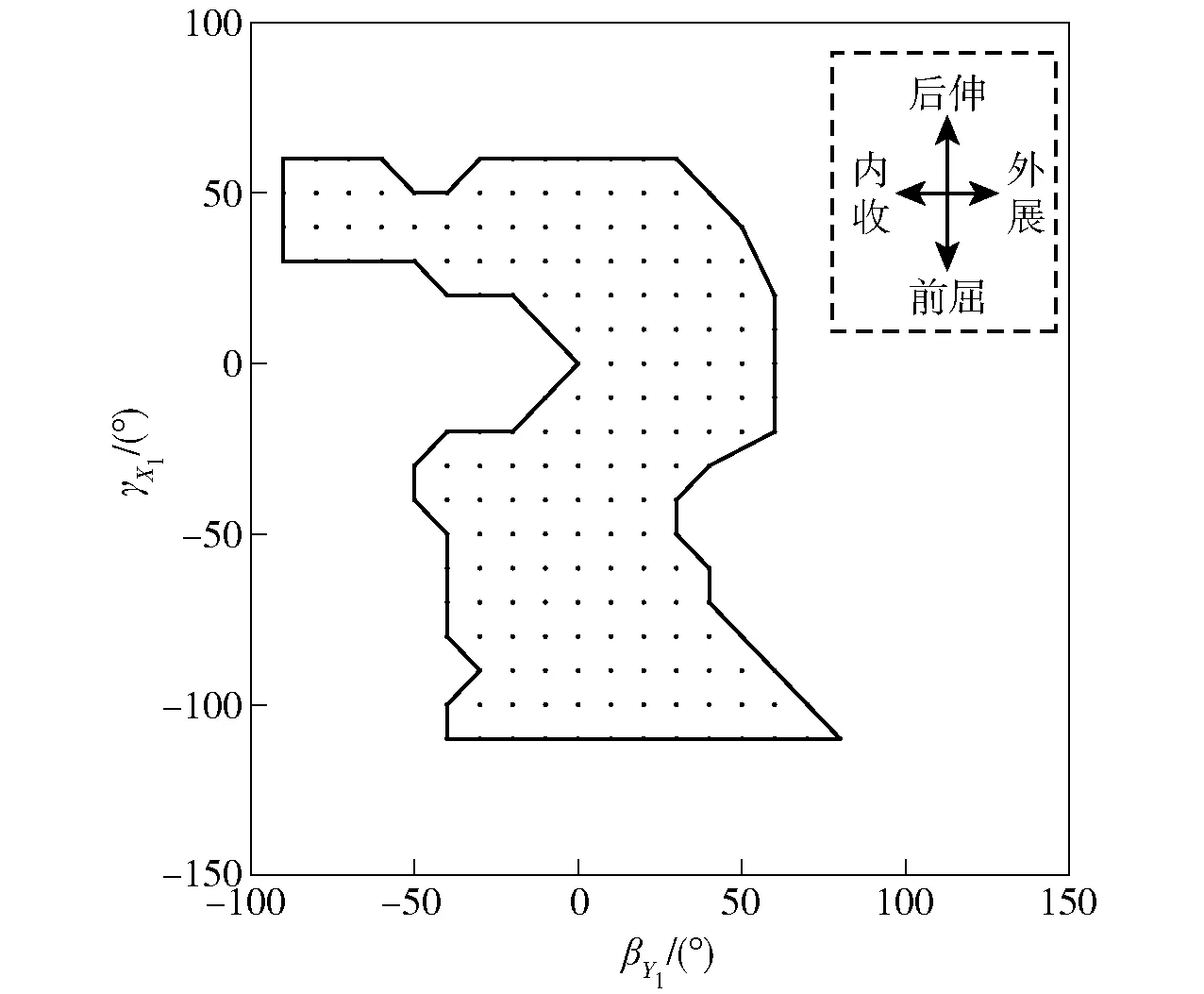
图5 仿真结果Fig.5 Simulated results
4 工作空间优化
机构参数和约束条件不同都会影响工作空间的点集数量,因此姿态工作空间的最优化设计,属于全局最优问题。在选定的主要影响工作空间大小的设计参数取值范围内,寻找满足约束条件的最优解,达到点集数量最多的设计目标。
4.1 评价指标
该并联机构作为仿人肩关节,不仅要考虑结构参数对点集数量的影响,还要考虑该并联机构的姿态工作空间区域相对于人体肩关节活动区域的实现程度。因此,将人体肩关节灵活活动区域的大小设定为基准值[25]RV,张文增[9]基于高速摄像的人体运动检测系统,采用基于标记点的图像处理方法,有效地计算出人体上肢运动参数,肩部前屈后伸的运动范围为-30°~100°,肩部外展内收的运动范围为-30°~120°,将上述数据转化成姿态工作空间的点集,如图6所示。

图6 人体肩关节灵活活动区域Fig.6 Flexible region of human shoulder joint
将姿态工作空间点集数量的相对值作为评价指标[25]WSRV,其公式为
(38)
4.2 参数优化
为了清晰直观地表征该并联机构的各结构参数对工作空间的影响,本文通过控制变量法,将多因素问题变成多个单因素问题,提出一种基于多参数的迭代抽样优化方法。首先将结构参数初始化组合,分别在各个结构参数取值范围内按均匀分布进行抽样,统计各抽样值的评价指标;然后将各组最优评价值所对应的参数值重新组合,在此基础上再次进行上述的各组抽样、统计和重新组合步骤,直至参数组合值与在其基础上得到的重新组合值误差不大于误差δ时优化结束。
表2为各结构参数取值范围。按照上述基于多参数的迭代抽样优化方法进行实验仿真,得到各结构参数对姿态工作空间的影响,如图7所示。

表2 结构参数取值范围
由图7(a)和图7(b)可知:在结构参数分别为α1=90°、α2=50°时WRSV取得最大值;由图7(c)可知:当α3=67°时WRSV取最大值,但考虑连杆A1B1加工工艺,选取α3=60°;由图7(d)可知:当r1为55~70 mm时WSRV取最大值并保持不变,考虑转动副C1、C2的加工特点及装配工艺性,选取r1=70 mm;由图7(e)可知:选取r2=90 mm;由图7(f)可知:WSRV呈现阶梯形增长的特性,考虑机构的紧凑性,选取d3=185 mm. 综上所述,选取了一组较合理的结构参数:α1=90°、α2=50°、α3=60°、r1=70 mm、r2=90 mm、r3=185 mm. 在这组结构参数下,该并联机构的姿态工作空间优化结果如图8所示。

图7 结构参数优化Fig.7 Optimization of structure parameters

图8 优化结果Fig.8 Optimized result
相比初始结构参数下的工作空间(见图5),图8所示的工作空间大小有明显的增大,并且该工作空间达到了人体肩关节灵活活动区域(见图6)的95%.
5 实例计算验证
根据仿人肩关节的结构参数:α1=90°、α2=50°、α3=60°、r1=70 mm、r2=90 mm、r3=185 mm,在MATLAB软件中验证位置解解析,在Adams软件中验证雅可比矩阵。
5.1 验证位置解解析式
验证步骤如下:
1)给定一组输入转动副角度,如表3第2列和第3列所示。
2)根据该并联机构的位置正解解析式计算出机构的姿态,如表3第4列和第5列所示。
3)将上述姿态带入该并联机构的位置反解解析式,求得输入转动副角度,如表3第6列和第7列所示。
4)比较步骤1与步骤3的角度差可知,误差极小,从而验证了解析式的正确性。
5.2 验证雅可比矩阵
验证方法和步骤如下:
1)给定一组输入转动副角度,如表4、表5第2列和第3列所示,并设定输入转动副角速度恒定均为1°/s.
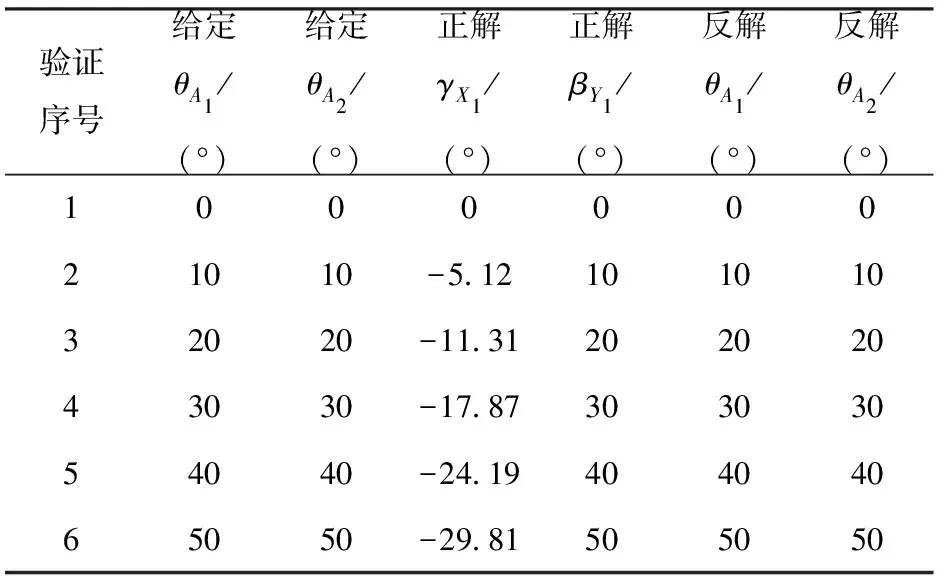
表3 验证位置解解析式
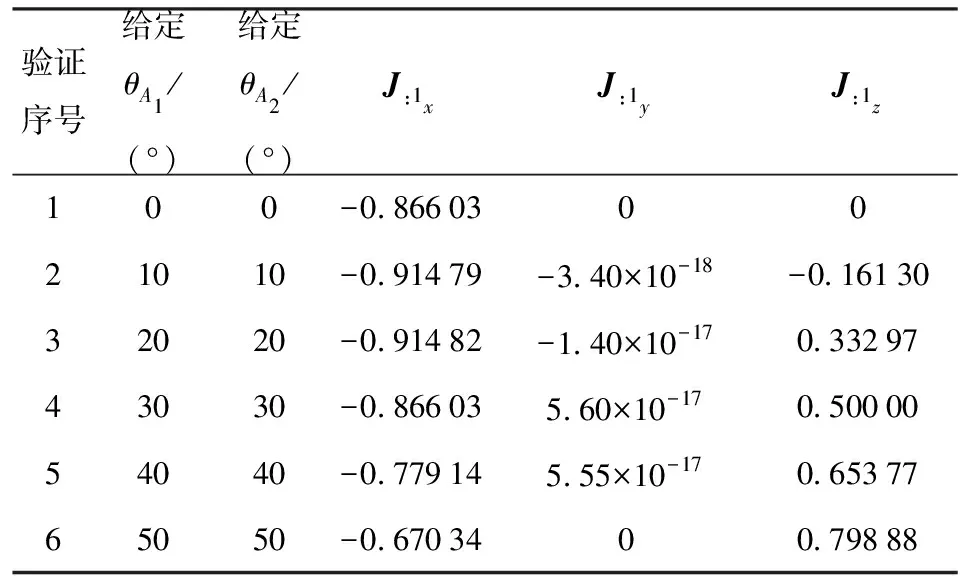
表4 雅可比矩阵第1列J:1

表5 雅可比矩阵第2列J:2
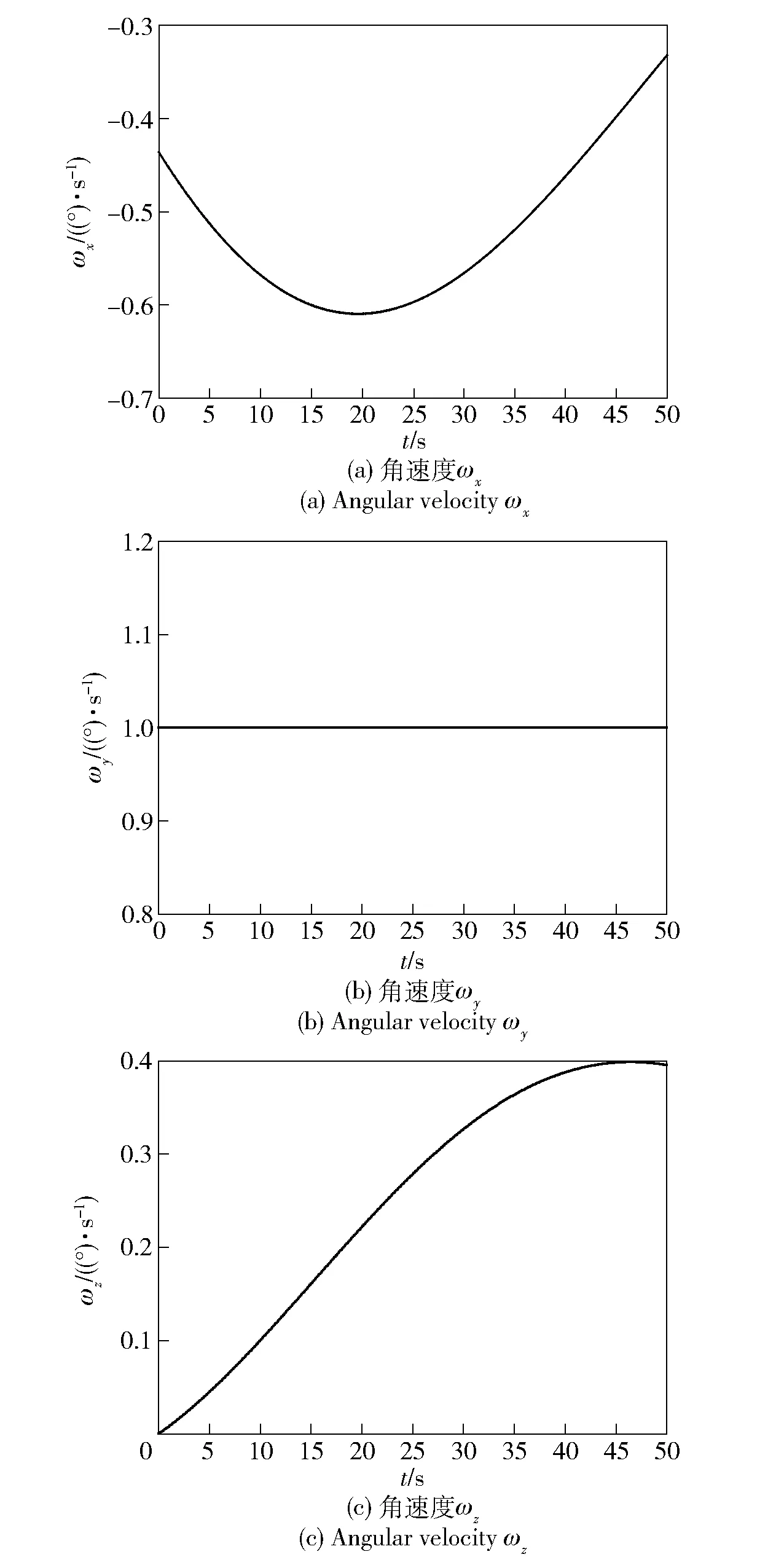
图9 动平台角速度Fig.9 Angular velocity of moving platform
2)根据该并联机构的雅可比矩阵解析式计算出雅可比矩阵,雅可比矩阵第1列如表4第4、第5、第6列所示,雅可比矩阵第2列如表5第4、第5、第6列所示。
3)在Adams软件中建立该并联机构模型,设定驱动器角速度恒定均为1°/s,仿真时间50 s,动平台输出角速度与时间的关系曲线如图9所示。
4)比较步骤2与步骤3的数值差可知,二者误差极小,从而验证了雅可比矩阵的正确性。
6 结论
1)运用Paden-Kahan子问题方法可求得并联机构中所有运动副的反解,与现有方法比较,简化了位置反解条件的判定,易于编程。
2)基于旋量理论和指数积公式的机构雅可比求解方法,具有明确的几何意义,避免了复杂的求导过程,简化了运算过程。
3)这种仿人肩关节具有结构紧凑,解耦性强和加工装配工艺性好等优点,并且其工作空间符合人体肩关节运动特点。

