基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化

刘超越， 张成

(北京理工大学 宇航学院, 北京 100081)

0 引言

飞行器多阶段轨迹规划可以实现飞行器在不同飞行环境、不同飞行要求下的飞行状态切换。在多阶段轨迹规划方面，航天工程中有许多应用研究，如商用飞机飞行规划问题[1-3]、航向辅助轨道转移问题[4]等。然而，多阶段轨迹规划在导弹弹道优化问题中的应用数量有限。文献[5-6]对炮射滑翔制导导弹进行了多阶段轨迹规划，将整个弹道轨迹划分为4个相互连接的飞行阶段，利用高斯伪谱法(GPM)将轨迹规划问题转化为非线性规划问题，实现了相应的飞行任务。

二级助推战术火箭与炮射滑翔制导导弹相比，具有速度快、突袭性好、射程远等优点。根据其作战任务，发射前必须确定一些关键变量[7-8]，包括二级助推发动机的点火时间、制导启动时间、制导阶段的控制等。这些变量对弹道性能有很大影响，如射程、攻击速度、攻击角度等。

上述关键变量的确定过程可以看作是一个终端时刻自由、终端状态固定且带有路径约束的多阶段、非线性最优控制问题。求解最优控制问题的数值方法很多，一般分为间接法和直接法[9]。间接法将最优控制问题转换为Hamilton边值问题，通过数值方法求解，存在收敛域小、难以估计共轭变量初值等不足，且二级助推战术火箭轨迹优化问题存在多个路径约束，使间接法的推导过程十分复杂。直接法采用参数化方法，将连续空间的最优控制问题求解转化为非线性规划(NLP)问题，通过数值求解NLP问题获得最优解。由于直接法克服了间接法的诸多不足，目前在飞行器轨迹优化领域得到了更广泛应用[10]。

本文研究的GPM是直接法的一种，它采用全局插值多项式在一系列勒让德- 高斯 (LG)点上近似状态变量和控制变量。与一般的配点法相比，GPM能够以较少节点获得较高的求解精度，同时，根据GPM共轭变量映射定理[11-13]，采用GPM转化得到NLP问题的库恩- 塔克条件(KKT)与原最优控制问题1阶最优必要条件的离散形式具有一致性。因此，GPM因其高效、快速收敛和避免显式数值积分等优点，在求解最优控制问题方面得到了广泛应用[14-15]。

文献[16]研究了GPM在二级助推导弹多阶段轨迹规划问题中的应用，得到了最大纵向航程和最大横向航程两种最优轨迹，但二级助推发动机的点火时间、制导启动时间以及初始弹道倾角并不能根据飞行任务而改变，无法很好地利用二级助推导弹的优势，对不同的飞行任务适应性也相对较弱。文献[17]研究了二级助推导弹的多阶段轨迹规划问题，并确定了二级助推发动机的点火时间、制导启动时间等关键变量，但其研究仅在纵向平面内进行，无法进一步考虑导弹攻击目标过程中对禁飞区等战场环境约束区的规避情况。

为了较好地模拟导弹飞行过程中的真实飞行环境，需要考虑飞行过程中的协同禁飞区、敌方火力覆盖区等战场环境约束。然而，使用GPM解决复杂约束下的多阶段轨迹规划问题时，出现以下困难：1)在区间内部，离散节点的分布相对较稀疏，使得规划轨迹在战场环境约束区附近精度较低，从而降低了高精度轨迹的求解效率；2)不正确的初值猜测可能导致最优解局部收敛甚至发散。针对以上两个问题，本文提出了基于准接触点的制导攻击段分段策略，以提高规划轨迹在战场环境约束区的求解精度和求解效率。同时，提出了基于初值生成器的迭代策略，以提高最优解的收敛速度和可行性。

本文以二级助推战术火箭为研究对象，建立战术火箭对地攻击的数学模型，将其描述为带有路径约束的多阶段最优控制问题；利用GPM将该最优控制问题的变量进行离散化；结合基于准接触点的制导攻击段分段策略对弹道进一步分段；利用基于初值生成器的迭代策略，求解战场环境约束等多种约束条件下二级助推战术火箭的多阶段轨迹优化问题，同时确定二级助推发动机的点火时间、制导启动时间、初始弹道倾角、制导阶段的控制等关键变量。

1 二级助推战术火箭对地攻击数学模型

1.1 战术火箭3自由度质点运动学模型

在战术火箭对地攻击任务中，战术火箭的运动主要以航迹控制为主，因此采用三维空间的3自由度质点模型即可满足要求。

战术火箭在地面坐标系下的质点运动方程为

(1)

式中：(x,y,z)为战术火箭在地面坐标系中的位置坐标；v为战术火箭的飞行速度；θ为弹道倾角；ψv为弹道偏角；m为战术火箭质量；P为发动机推力；Fx为阻力；Fy为升力；Fz为侧向力；η为燃料的质量秒流量；α为攻角；β为侧滑角。定义状态向量x=[v,θ,ψv,x,y,z,m]T，控制向量u=[α,β]T。

战术火箭在飞行过程中受到的空气阻力、升力和侧向力的计算公式为

(2)

式中：0.5ρv2为动压；ρ为大气密度；S为战术火箭参考横截面积；Cd、Cl和Cc分别为阻力系数、升力系数和侧向力系数，三者均为攻角、侧滑角和马赫数的函数。

气动数据的拟合效果会对飞行轨迹设计产生重要影响。对于战术火箭，阻力系数可看作是关于α和β的二次函数，升力系数可看作是关于α的线性函数，侧向力系数可看作是关于β的线性函数。将本文中战术火箭的气动数据拟合，得到的拟合结果为

(3)

式中：Ma为马赫数；a1=-0.108 8，a2=10.740 0，a3=0.217 1；b1=-0.985 5，b2=10.040 0；c1=-0.985 5，c2=10.040 0.

战术火箭在大气层内飞行，将标准大气密度ρ、声速c进行精确拟合：

(4)

式中：T为大气温度，T=292.6-0.010 39y+4.497×10-7y2-6.639×10-12y3.

1.2 弹道阶段的划分

二级助推战术火箭的飞行过程可以分为4个阶段：发射段、爬升段、续航段和制导攻击段，如图1所示。在不同的飞行阶段，飞行参数以及运动学模型有所不同。每个阶段的具体表述如下：

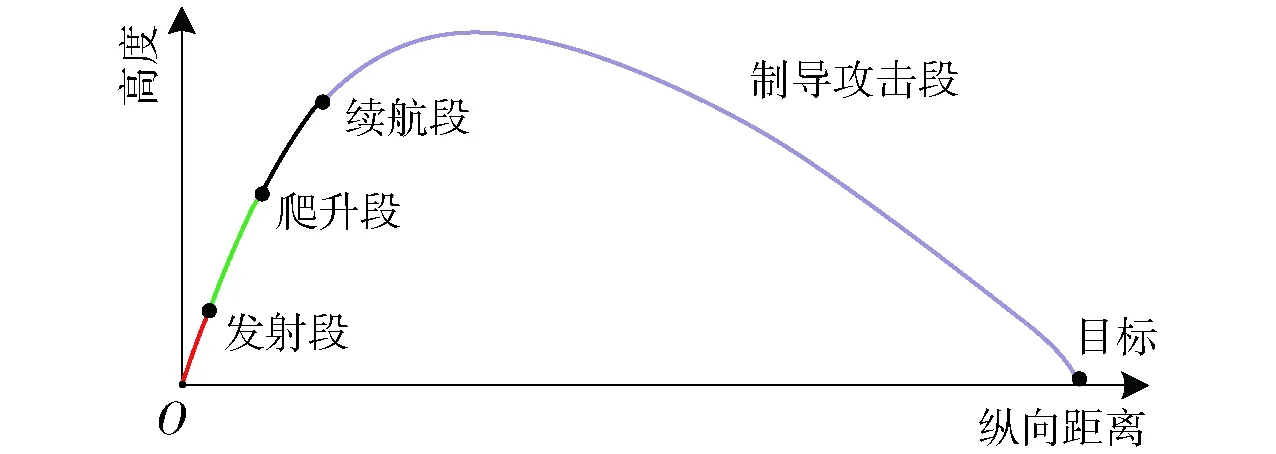
图1 弹道分段Fig.1 Division of trajectory

1)发射段：始于发射点，结束于1级发动机的关机点，为无控飞行状态。1级发动机可为战术火箭在飞行初期提供较高的飞行速度。发射段时长固定，为1级发动机的工作时间，设为[t0,t1]。

2)爬升段：始于1级发动机的关机点，结束于2级发动机的点火点。1级发动机工作结束后，火箭进入爬升段，继续以无控飞行状态爬升。爬升段连接发射段与续航段，目的是将战术火箭续航段的开始时刻调整至最佳时机。因此，爬升段的工作时间不固定，设为[t1,t2]。

3)续航段：始于2级发动机的点火点，结束于2级发动机的关机点，为无控飞行状态。在续航段，2级发动机工作将战术火箭姿态和速度调整至最佳状态，为适应战场环境、攻击目标做好充分准备。续航段时长固定，为2级发动机的工作时间，设为[t2,t3]。

4)制导攻击段：始于2级发动机的关机点，结束于目标点。在制导攻击段，战术火箭通过舵的控制，不断修正飞行路径，在满足复杂战场约束情况下，精确攻击目标。制导攻击段的工作时间不固定，设为[t3,t4]。

1.3 约束条件

战术火箭的对地攻击轨迹需要满足下列约束条件：

1.3.1 边值约束

1.3.1.1 初值约束

(5)

式中：t0为发射时刻；(x0,y0,z0)为发射点坐标；θ(t0)为初始弹道倾角，是轨迹优化问题中的离散变量，需要根据不同的任务确定最优值。

1.3.1.2 终端约束

为了保证战术火箭的杀伤效能，需要战术火箭攻击目标时具有较高的速度与较大的落角，因此轨迹优化问题的终端约束为

(6)

式中：tf为终端时刻；vfmin和θfmin分别为终端最小攻击速度和最小落角；(xt,0,yt)为目标坐标。

1.3.2 多阶段约束

由于在整个弹道的不同阶段，战术火箭的工作情况不同，需要施加不同约束。另外，战术火箭质量随着1级发动机及2级发动机的工作发生变化。

1)发射段

(7)

2)爬升段

(8)

3)续航段

(9)

4)制导攻击段

(10)

式中：P1、η1和P2、η2分别为1级发动机和2级发动机的推力、质量秒流量；αmax和αmin分别为攻角可行域的上限和下限；βmax和βmin分别为侧滑角可行域的上限和下限。

1.3.3 战场环境约束

战术火箭在攻击目标过程中，需要规避协同禁飞区和敌方火力覆盖区等战场环境约束区域[18]，提高战术火箭的生存能力和攻击目标的有效性。

对于协同禁飞区，其上方很大高度范围之内战术火箭都是无法穿越的，因此本文采用无限高的圆柱体模型，所规划的轨迹不能与该圆柱相交。约束条件式为

‖(x(t)-xnf,i,z(t)-znf,i)‖2≥rnf,i，
i=1,2,…,Nnf，

(11)

式中：‖·‖2为两点之间的距离；(xnf,i,0,znf,i)和rnf,i分别为第i个协同禁飞区的中心坐标及半径。

敌方火力覆盖区的作用范围可近似看作半球，因此相应的约束条件式为

‖(x(t)-xfc,i,y(t)-yfc,i,z(t)-zfc,i)‖2≥rfc,i，
i=1,2,…,Nfc，

(12)

式中：(xfc,i,yfc,i,zfc,i)和rfc,i分别为第i个敌方火力覆盖区的中心坐标及半径。

1.3.4 过载约束

为了确保战术火箭飞行过程中的结构安全，需要考虑过载约束：

(13)

式中：nl为过载；nlmax和nlmin分别为过载约束的上限和下限。

1.3.5 内点约束

在多阶段的轨迹规划问题中，需要确保每一阶段和下一阶段的时间、状态等是紧密连接的。因此，需要在阶段边界上施加强制连接条件，即

(14)

式中：k(k=1,2,…,K)为阶段数；K为所有阶段的个数；tP1和tP2分别为1级发动机和2级发动机的工作时间。

1.4 目标函数

考虑到战术火箭执行攻击目标任务时兼备时间较短和控制量较省的性能，目标函数由两部分构成：1)总飞行时间的最小化；2)飞行过程中控制量的最小化。本文中，控制量是指攻角和侧滑角，为了使积分项处于相同的数量级，对攻角和侧滑角进行归一化处理。因此，目标函数可以描述为

(15)

式中：λ为调整总飞行时间和总控制量在目标函数中所占权重的权重因子。

1.5 最优控制问题框架

将轨迹规划问题转化为最优控制问题：寻找控制变量u=[α,β]T，最小化积分型性能指标：

(16)

式中：x=[v,θ,ψv,x,y,z,m]T∈R7为状态变量；t∈[t0,tf]，终端时间tf自由；L为目标函数(15)式的被积函数。满足如下运动学微分方程约束(见(1)式)：

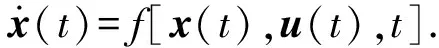
(17)

边界条件(见(5)式和(6)式)：

Bmin≤B(x(t0),x(tf),t0,tf)≤Bmax，

(18)

式中：B为边值约束的简化形式；约束的上限和下限符号分别为Bmax和Bmin. 路径约束(见(11)式～(13)式)：

Cmin≤C(x(t),u(t),P,η)≤Cmax，

(19)

式中：C为路径约束的简化形式；约束的上限和下限符号分别为Cmax和Cmin.

2 多阶段最优控制问题离散化

GPM将最优控制问题的状态变量和控制变量在一系列LG点上离散，并以离散点为节点构造拉格朗日插值多项式来逼近状态变量和控制变量。通过对全局插值多项式求导来近似状态变量对时间的导数，从而将微分方程约束转换为一组代数约束。性能指标中的积分项由高斯积分计算。终端状态由初始状态加右端函数在整个过程的积分获得。经上述变换，可将最优控制问题转化为具有一系列代数约束的NLP[19-20]。

2.1 时域变换

在前边介绍的多阶段轨迹优化问题中，时间间隔t∈[t0,tf]被划分成K个阶段Sk=[tk-1,tk],k=1,2,…,K. 采用GPM计算最优控制问题时，需要通过(20)式将每段时间区间转换到[-1,1]：

(20)

2.2 状态变量与控制变量的插值近似

GPM需要在一系列离散点上对状态变量和控制变量进行全局插值多项式逼近。在Sk中，采用拉格朗日插值多项式作为基函数来近似状态变量和控制变量：

(21)

(22)

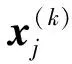
2.3 微分方程的约束转换为代数约束

对全局插值多项式(21)式微分后，代入运动学微分方程(17)式中，并在LG点上离散，可得

(23)

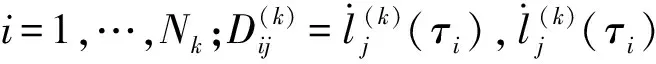
2.4 约束条件离散化

边界约束(见(18)式)表示为

(24)

在LG点对路径约束(见(19)式)进行离散化处理，得

(25)

则内点约束(14)式可表示为

(26)

最后，目标函数(16)式可用高斯求积公式进行离散化表示：

(27)

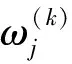
至此，多阶段连续最优控制问题被转化为离散参数的NLP问题，其标准形式为

(28)

式中：F(z)为性能指标函数；ge(z)为不等式约束；hf(z)为等式约束；p、q分别为不等式约束和等式约束的个数；决策向量z=[(z(1))T,(z(2))T,…,(z(k))T,…,(z(K))T]T，包括离散状态量、离散控制量、各阶段间的连接时刻和终端时刻，

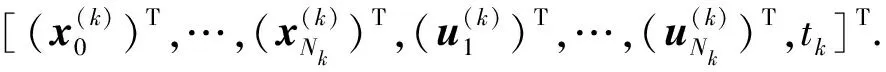
(29)

由于IPOPT求解器采用内点算法，可以处理具有大量等式和不等式约束的大规模稀疏非凸问题。为了解决NLP，本文采用开源的NLP求解器IPOPT.

3 最优轨迹的求解策略

3.1 基于准接触点的制导攻击段分段策略

GPM是将连续最优控制问题离散化后进而求解的数值方法，LG点为勒让德多项式的根。由LG点的分布规律可知：越靠近区间边界处LG点越密集；在区间的内部则LG点相对稀疏。作为一种路径约束，战场环境约束若处于规划轨迹的区间边界处，则战场约束区附近的规划轨迹精确度较高；战场环境约束若处于规划轨迹的区间内部，则战场约束区附近的规划轨迹精确度会降低；甚至，当区间内部LG点密度较低时，出现规划轨迹与禁飞区或敌方火力覆盖区相交的情况，如图2所示。因此，战场环境约束处于规划轨迹的区间内部时，较难得到高精度的解。

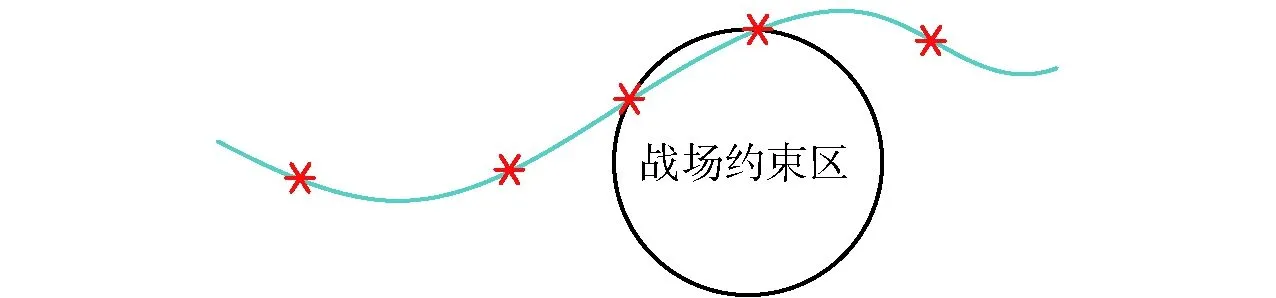
图2 轨迹与战场约束区相交Fig.2 Intersection between trajectory and battlefield constraint region

在本文所述战术火箭攻击目标的飞行过程中，发射段、爬升段和续航段距离发射点比较近，一般不会受到禁飞区、敌方火力覆盖区的干扰，因此，本文采用以准接触点为分段节点将制导攻击段进一步分段的策略[21]，以提高战场约束区附近规划轨迹的精确度，进而提高高精度最优轨迹的求解效率。

准接触点根据制导攻击阶段细分前预生成的规划轨迹来估计：制导攻击阶段细分前，选择较少的LG点快速解算得到最优轨迹，则战场约束区的边界会被最优规划轨迹分成一个优弧和一个劣弧，如图2所示；理论上，为了满足快速攻击和较少控制量的要求，最终高精度规划轨迹应沿战场约束区的边界飞行。显然，准接触点应该选取于战场约束区边界圆的劣弧上。为了有利于产生更平滑的轨迹并且减轻对机动性的需求，准接触点选取为劣弧中点。以准接触点为分段节点将制导攻击阶段进一步分段后，战场约束区附近的轨迹与LG点分布情况如图3所示。

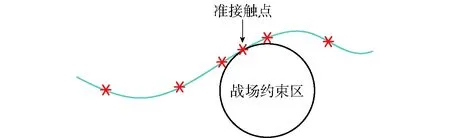
图3 采用制导攻击段分段策略时战场约束区附近轨迹Fig.3 Trajectory near battlefield constraint region for using the guided attacking segment subdivision strategy

3.2 基于初值生成器的迭代策略

在GPM实际应用中发现，不恰当的初值可能使问题收敛到不可行解[22-23]。针对这一问题，本文提出了改进的最优轨迹求解策略，即构造设计变量初值生成器，利用GPM能以较少节点获得较高精度的优点，提出如下多步迭代优化求解步骤：

步骤1对于未对制导攻击段进行阶段细分前的轨迹规划问题，先在4个飞行阶段采用较少的离散点，快速计算近似的最优轨迹和控制变量。

步骤2利用3.1节所述准接触点选取方法，根据步骤1求出的最优轨迹选取合适的准接触点；以选取的准接触点为分段节点，对制导攻击段进行进一步细分，得到最终的全弹道多阶段轨迹优化问题模型。

步骤3以步骤1得到的最优轨迹和控制量为参考，以较少的离散点计算步骤2得到的轨迹优化问题，得出近似最优轨迹和控制变量，通过插值获得更多离散点。

步骤4将步骤3获得的变量值作为初值重新求解，将得到的最优变量代回动力学微分方程组(1)式中测算误差；循环执行此步，直至得到足够高精度的解。

4 仿真验证与结果分析

4.1 仿真参数与结果

仿真中战术火箭的弹体参数以及约束的参数值分别如表1和表2所示。

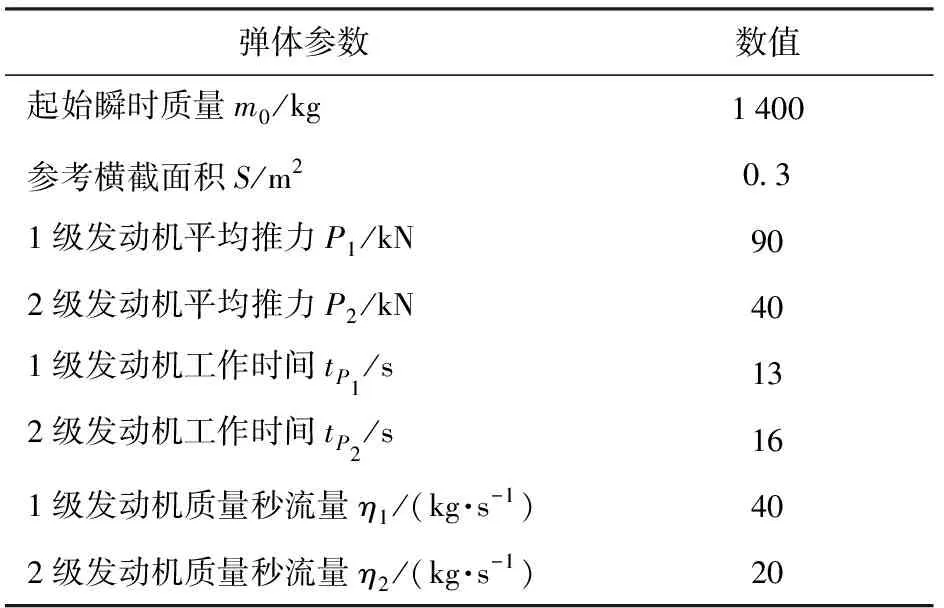
表1 弹体参数表

表2 约束参数表

构建仿真场景如下：战术火箭从发射点(x0,y0,z0)处，以某一弹道倾角发射，初始速度v0=10 m/s，弹道偏角ψv=0°，经历发射段、爬升段、续航段和制导攻击段后攻击位于(300 km,0 km,150 km)处的地面固定目标；在飞行过程中部署一个圆柱状协同禁飞区和一个半球状敌方火力覆盖区。构建两种不同仿真场景，每个场景的发射点位置、战场约束区中心位置以及半径如表3所示。

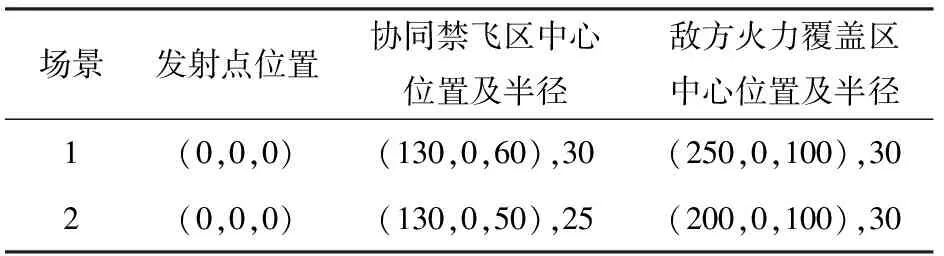
表3 仿真场景

为了使飞行任务兼备时间较短和能量较省的特点，令目标函数中的权重因子λ=2. 对构建的每个场景，在基于初值生成器的迭代策略下，分别针对制导攻击段分段、不分段两种情形，在相同的高求解精度以及分配相同总LG点个数情况下进行求解。计算在PC机上进行，CPU为Intel Core i7-3.6 GHz，应用基于MATLAB环境下的IPOPT软件包对NLP问题进行求解。仿真结果如图4～图9所示。

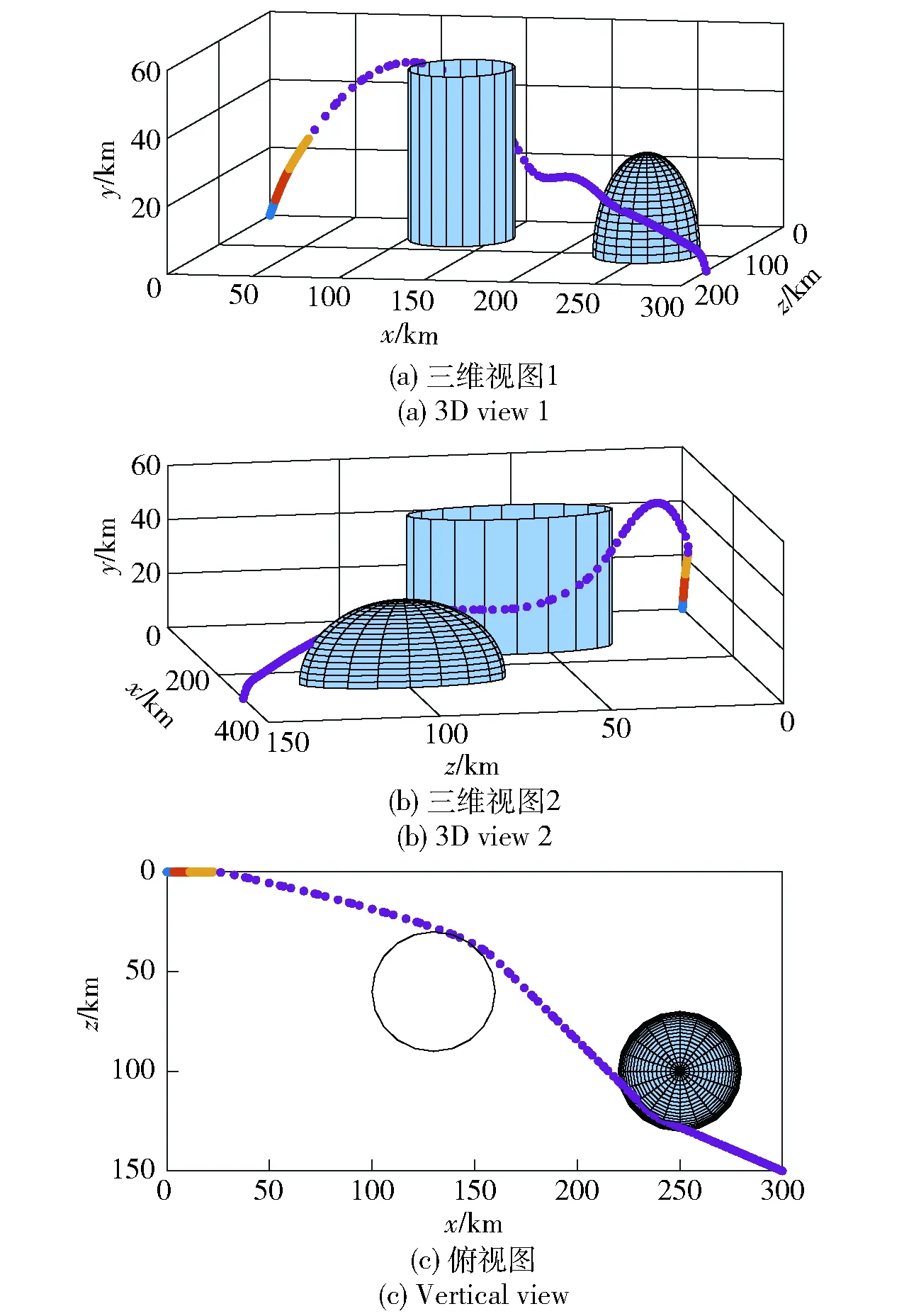
图4 场景1不采用制导攻击段分段策略时最优轨迹Fig.4 Optimal trajectory without the guided attacking segment subdivision in Scene 1

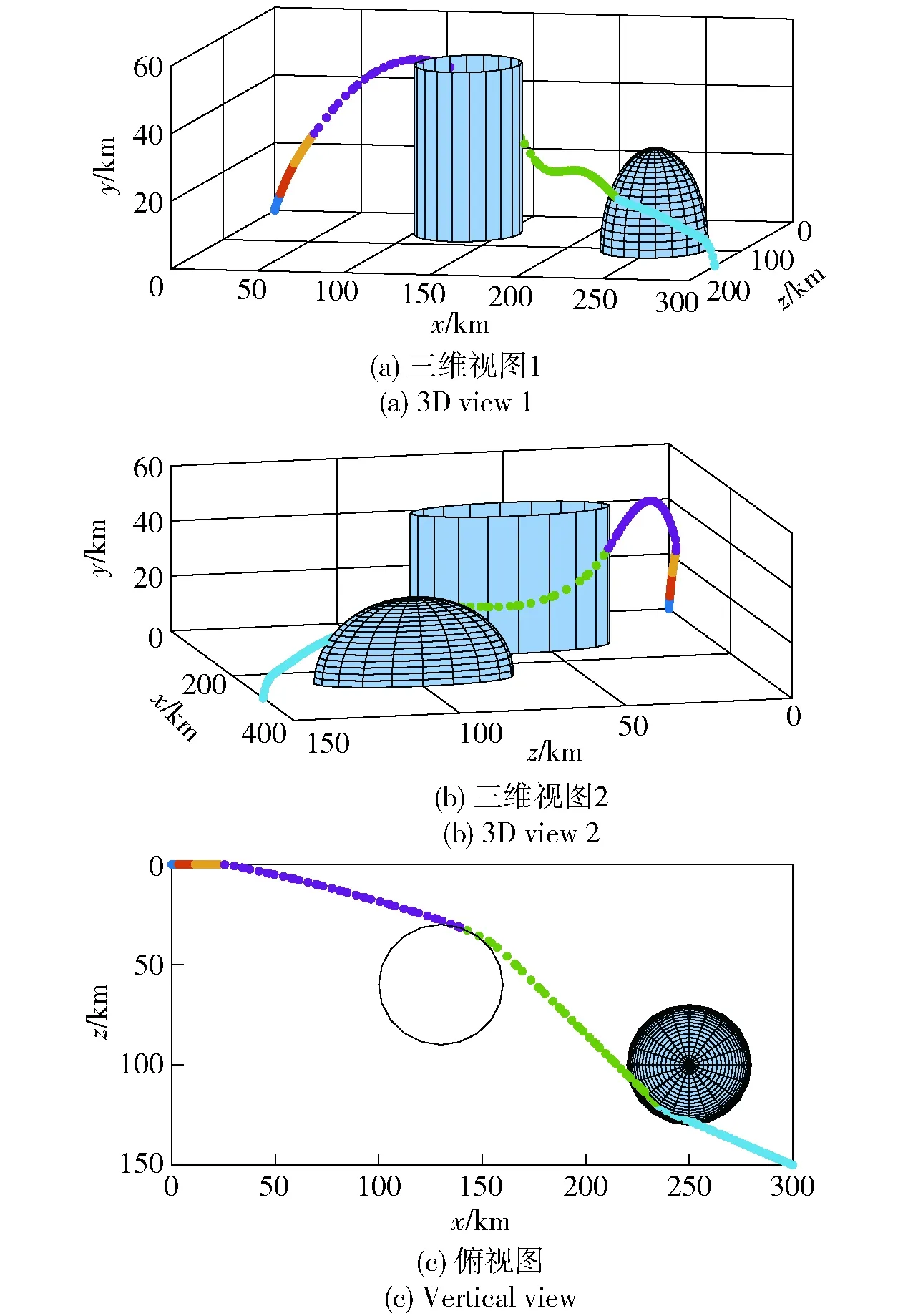
图5 场景1采用制导攻击段分段策略时最优轨迹Fig.5 Optimal trajectory with the guided attacking segment subdivision in Scene 1

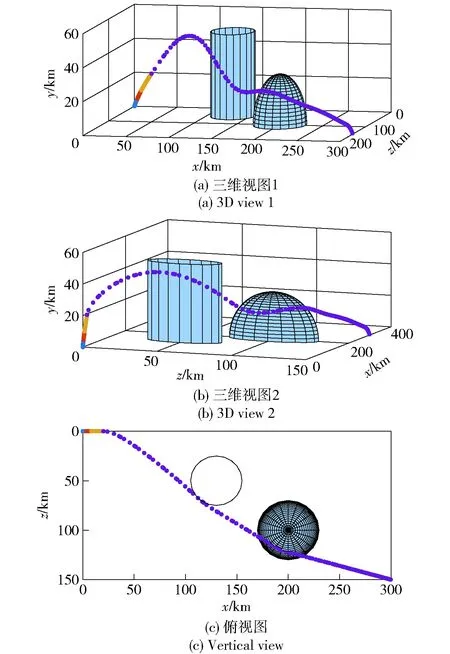
图6 场景2不采用制导攻击段分段策略时最优轨迹Fig.6 Optimal trajectory without the guided attacking segment subdivision in Scene 2

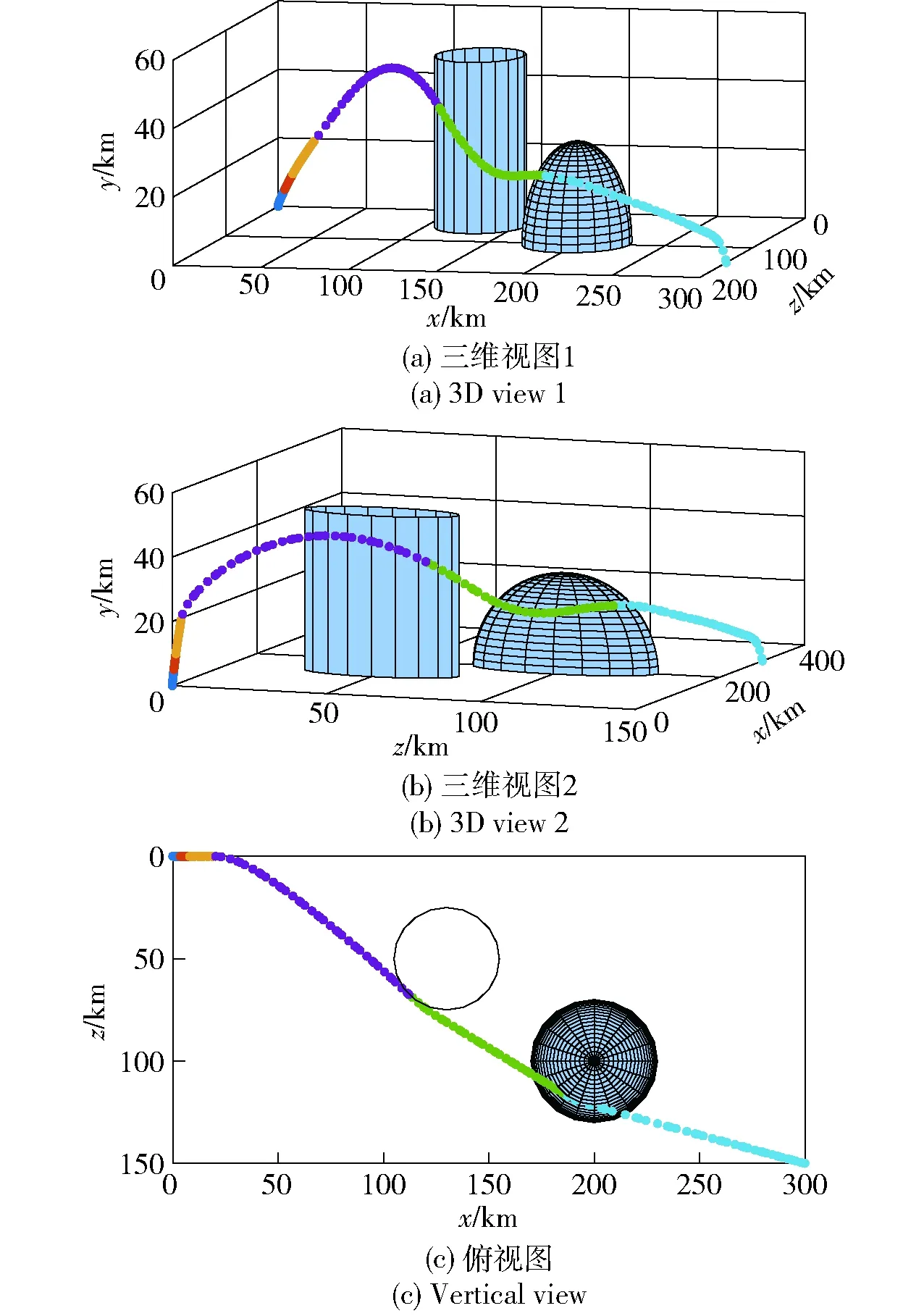
图7 场景2采用制导攻击段分段策略时最优轨迹Fig.7 Optimal trajectory with the guided attacking segment subdivision in Scene 2

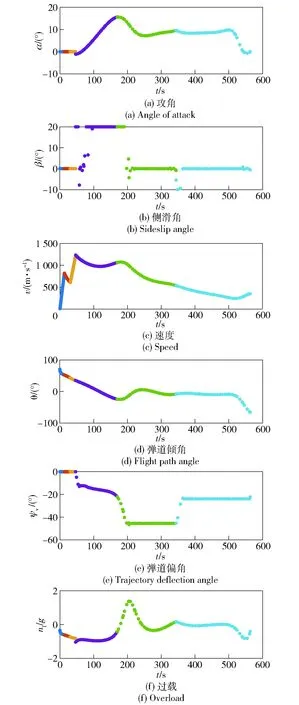
图8 场景1战术火箭飞行参数Fig.8 Flight parameters of tactical rocket in Scene 1

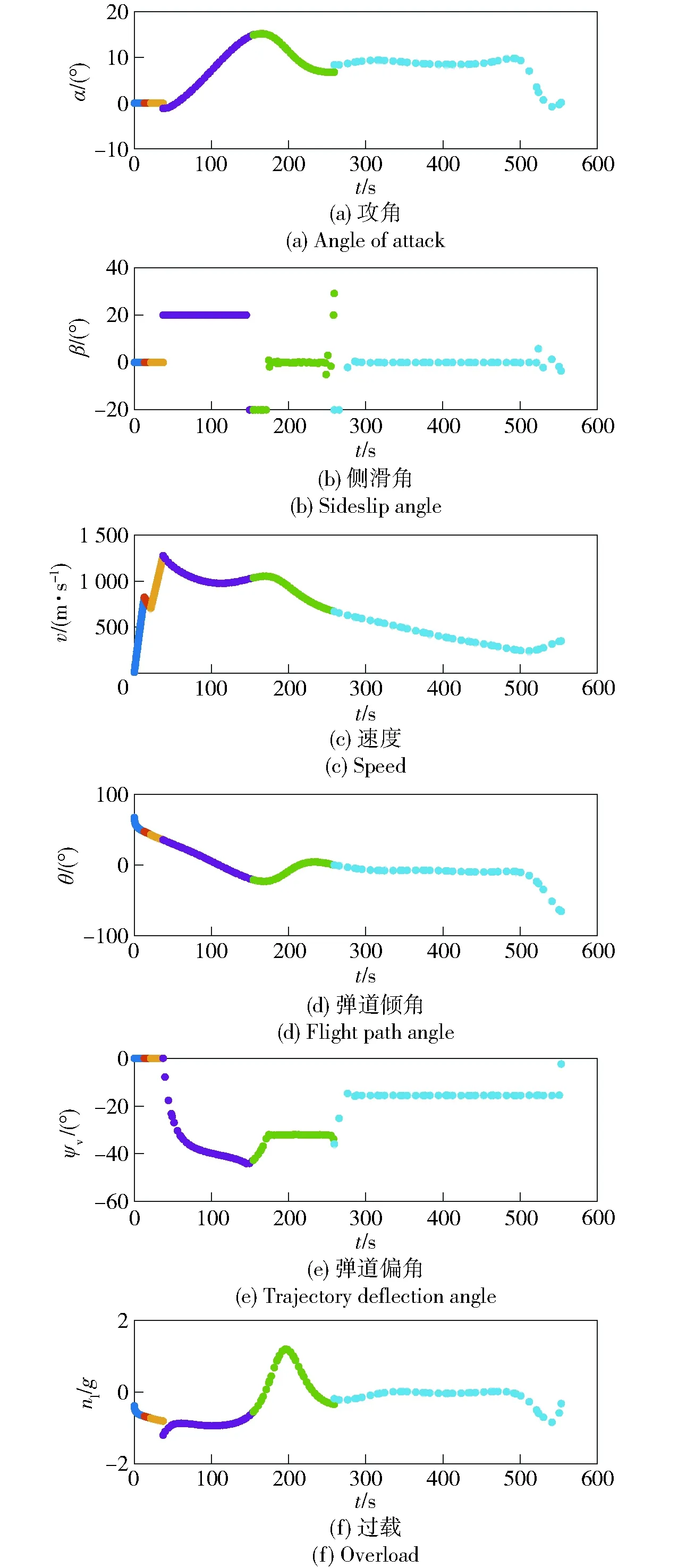
图9 场景2战术火箭飞行参数Fig.9 Flight parameters of tactical rocket in Scene 2

图4、图6分别为不采用制导攻击段分段策略时，场景1、场景2战术火箭攻击目标的最优轨迹；图5、图7分别为采用制导攻击段分段策略时，场景1、场景2战术火箭攻击目标的最优轨迹。由图4、图5和图6、图7对比可知，采用制导攻击段分段策略时求得的最优轨迹与不采用时一致，并且都能够避开协同禁飞区、敌方火力覆盖区，精准击中地面固定目标。

图8、图9分别为场景1、场景2对应的飞行参数曲线。从图8(a)、图9(a)中可以看出：在弹道最高点附近时，由于空气密度较小，攻角迅速增大以产生足够大的控制能力；其后随着飞行高度的降低，空气密度随之增加，攻角也逐渐减小；在弹道末端，为了获得期望的落角，攻角迅速减小。从图8(b)、图9(b)中可以看出，进入制导攻击阶段后，侧滑角较快趋于0°并保持至攻击目标时刻，达到了控制量较省的目的。从图8(f)、图9(f)中可以看出，整个飞行过程中的过载满足约束。

进一步增加仿真场景3、场景4如表4所示。分别对每个仿真场景在是否采用制导攻击段分段策略以及是否采用基于初值生成器的迭代策略不同条件下进行仿真验证。每个仿真场景的仿真结果关键参数如表5所示；每个仿真场景在不同仿真条件下求解的时间如表6所示。

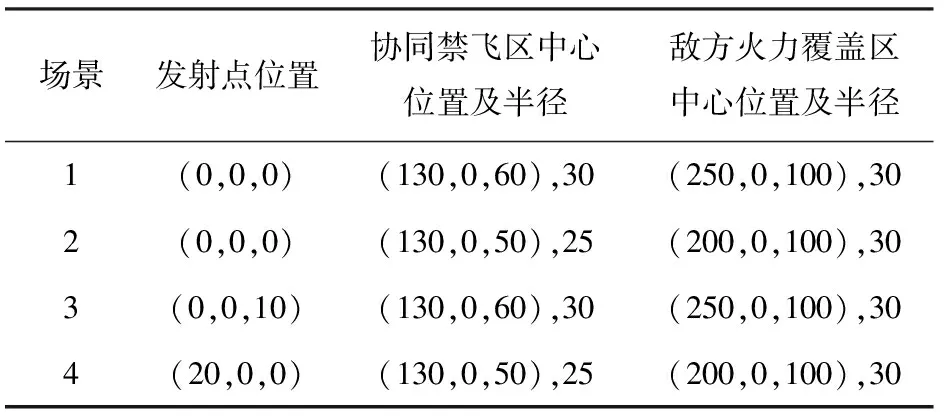
表4 仿真场景

由表5可知：战术火箭的最优初始弹道倾角和爬升段时长随不同的仿真场景下而变化，体现了二级助推战术火箭对不同发射地点、不同作战场景的适应性；4种仿真场景下，战术火箭的落速和落角均满足表2所设定的约束条件。

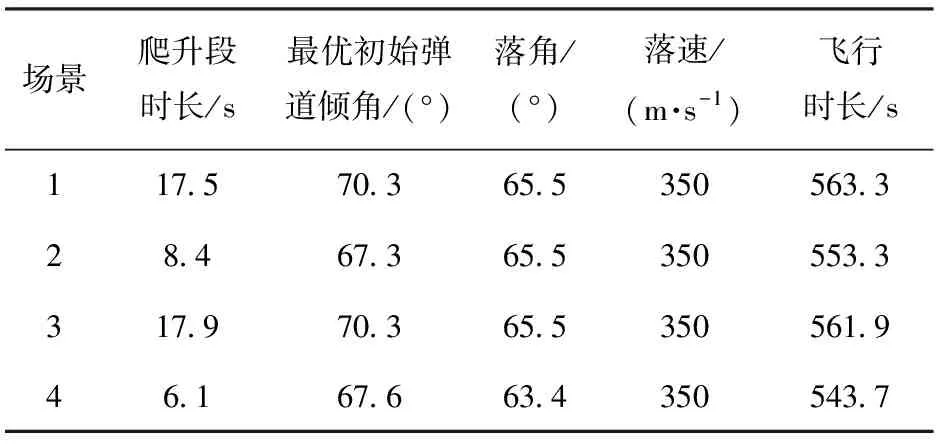
表5 仿真结果

由表6统计可知：当得到相同精度的解且总的LG点个数相同时，采用制导攻击段分段策略进行计算耗时比不采用分段策略的计算耗时短；同时，采用基于初值生成器的迭代策略进行计算耗时比不采用迭代策略耗时短。由此可知，采用以准接触点为分段节点对制导攻击段进行分段的策略，可以在战场约束区附近分配密度较高的LG点，有利于较快求得高精度的解；基于初值生成器的迭代策略可以加快求解的收敛速度，缩短求解时间。

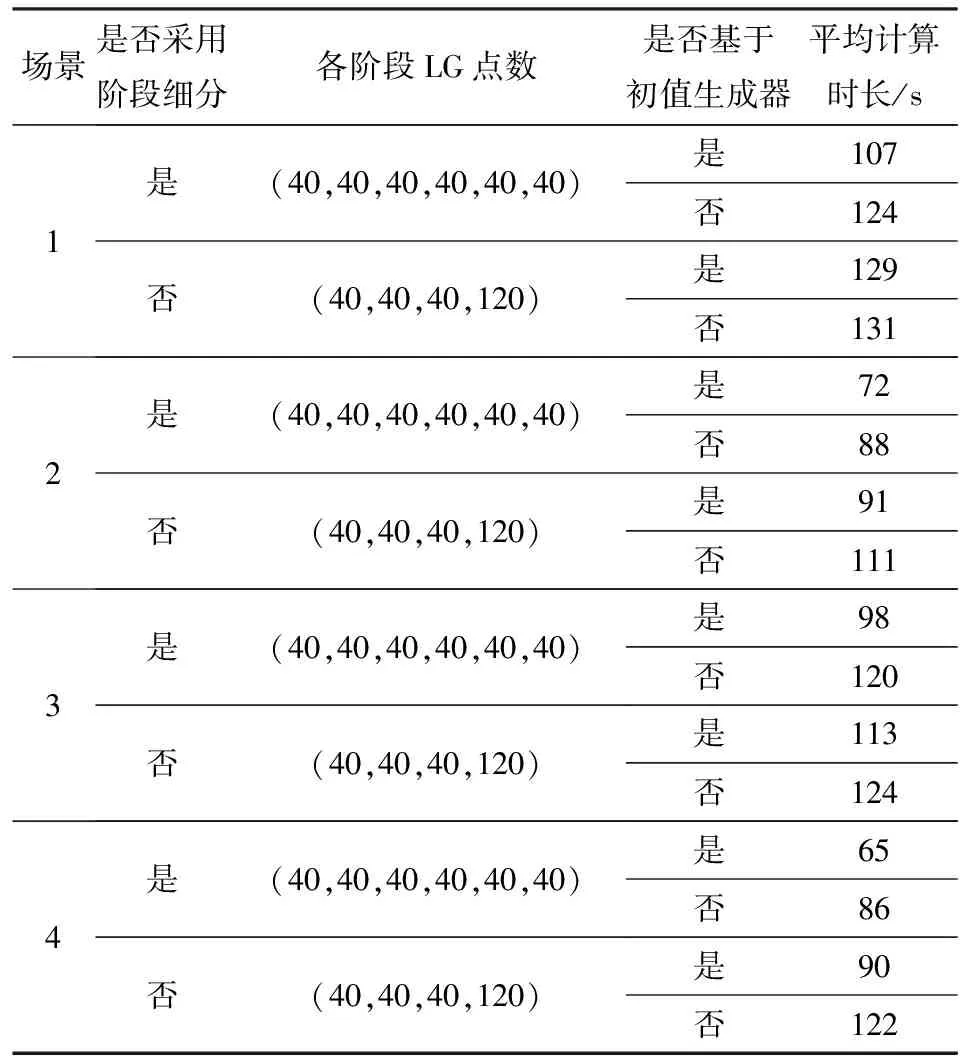
表6 仿真计算时间

4.2 仿真结果可行性验证

为了验证计算结果的可行性，将4个仿真场景分别求解后，最优控制量代入运动学微分方程中进行积分，并将得到的状态参数值分别与本文方法求得的最优状态量值进行对比，分析误差范围。4组结果中，相同时间插值点处的状态量绝对误差的最大值散点图如图10所示。由图10可见，GPM得到的最优解与数值积分结果的误差均在允许范围之内，从而验证了优化结果的可行性。

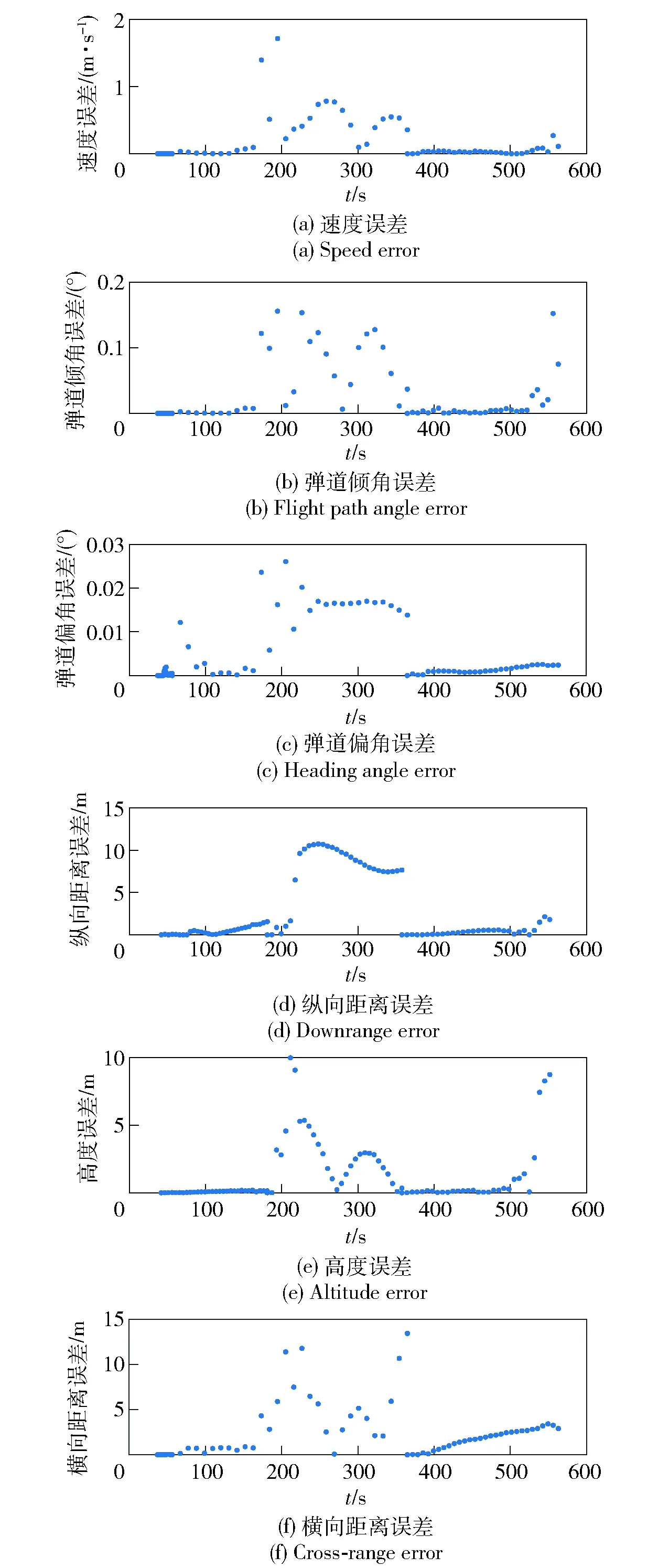
图10 误差散点图Fig.10 Error scatter figure

5 结论

本文研究了GPM在二级助推战术火箭多阶段轨迹优化设计中的应用，并提出了基于初值生成器的迭代策略以及基于准接触点的制导攻击段分段策略。仿真验证中对4种不同仿真场景下算法的时效性和可行性进行了分析。结果表明，采用该优化策略时，GPM能够保证较高的求解精度，并有效地提高优化轨迹的求解效率。