设置黏滞阻尼器的斜拉索参数振动模型及控制分析

汪峰 彭章 刘章军

摘要：为了掌握黏滞阻尼器对斜拉索参数振动的抑振效果，考虑拉索几何非线性、倾角以及桥塔和加劲梁的协同振动影响，建立了黏滞阻尼器一拉索一塔梁耦合体系的参数振动模型，推导了黏滞阻尼器作用下斜拉索的运动方程组，提出了控制拉索参数振动的阻尼器阻尼系数计算公式，并與传统单索模型对比，分析了塔梁协同作用对拉索固有频率的影响水平;编制计算程序比较了斜拉索安装阻尼器前后的振动位移时程特征，研究了三种典型索梁频率比下阻尼器的阻尼系数、安装位置对拉索参数振动的影响。结果表明：塔梁协同作用对拉索固有频率的影响水平与索力、索长密切相关，索力越小，索长越长，塔梁协同作用的影响率也越大。安装了黏滞阻尼器后，斜拉索的振动位移呈非线性衰减趋势;随着阻尼系数的增大，拉索的最大振幅逐渐减小，但其振幅衰减率呈现先增加后降低的趋势，系统存在一个最优阻尼系数;阻尼器安装位置距离索梁锚固端越远，拉索振幅越小，存在一个衰减率为零的临界安装位置，当阻尼器安装位置超过临界位置时，振幅不能持续衰减，阻尼器的抑振效率降低。

关键词：斜拉索;黏滞阻尼器;耦合模型;协同作用;参数振动控制

中图分类号：U448. 27;U441+.3

文献标志码：A

文章编号：1004-4523 （2019） 06-0977-09

D0I：10. 16 385/j. cnki. issn. 1004-4523. 2019. 06. 006

引言

斜拉桥是由斜拉索、桥塔和加劲梁构成的组合结构，因其跨越能力大，质量轻、造型美观，已成为大跨度桥梁的首选。但斜拉桥的索梁体系自阻尼小，在车辆、风雨、地震等复杂环境载荷作用下，拉索极易产生低频、高幅、持续的振动[1]。斜拉索的强烈振动会引起索梁锚固区出现疲劳裂纹，拉索保护层脱落等病害[2]，影响桥梁结构的使用和安全性能。近年来，通过对某些服役期大跨度斜拉桥的振动观测表明[3]，在微风细雨时某些拉索会发生1m以上的振动幅值，普遍认为这是由桥塔或桥面激励引起的参数振动，不同于强风雨激振。

目前，斜拉索振动控制多采用工作机理简单、造价低、易于维护的外置式黏滞阻尼器。针对斜拉索黏滞阻尼器的抑振机理和效果问题，国内外学者开展了广泛研究。巫生平等[4]结合某斜拉桥有限元模型，研究了不同阻尼器布设位置对桥梁位移、内力的影响，提出了利用最小二乘回归分析得到最优阻尼参数的方法。周海俊等[5]构建了拉索一阻尼器一弹簧系统，推导了系统的运动方程及特征频率方程，求出两种不同工况下系统阻尼比和频率的近似解析解，研究了系统最大模态阻尼比和拉索振动频率的变化规律。段元锋等[6]基于斜拉索一阻尼器系统模型，通过变量分离、参数统计等方法，提出了可近似独立衡量各参数影响的黏滞阻尼器实用设计方法。陈文礼等[7]建立了阻尼器一水平索耦合振动模型及其运动方程，以两根不同长度的拉索为对象，研究了拉索垂度对阻尼器控制效果的影响，发现阻尼器对小垂度拉索的控制效果更好。龚平等[8]将拉索简化为弹簧单元，建立了斜拉桥动力学模型，研究了拉索对全桥竖向振动频率的影响。

上述研究为斜拉索的振动控制提供了坚实的理论基础，但建立斜拉索一阻尼器体系力学模型时，大部分研究忽略了桥塔和加劲梁的协同振动影响，这种简化处理是否能满足拉索抑振设计的精度要求，尚未有明确的结论。因此，为了更加准确的掌握黏滞阻尼器的参数设置对拉索防振的影响，结合文献[9-10]的研究成果，考虑塔梁协同作用，引入黏滞阻尼器，构建斜拉桥塔一索一梁结构体系的耦合参数振动模型，提出控制拉索参数振动的最优黏滞阻尼器系数计算公式，分析塔梁协同作用对拉索固有频率的影响水平，比较斜拉索受控前后的拉索振动位移特征。研究黏滞阻尼器的阻尼系数、安装位置对拉索参数振动的影响规律，研究结果为大跨度斜拉桥减振设计提供理论依据。

1 阻尼器一拉索一塔梁耦合振动模型

1.1 基本假定

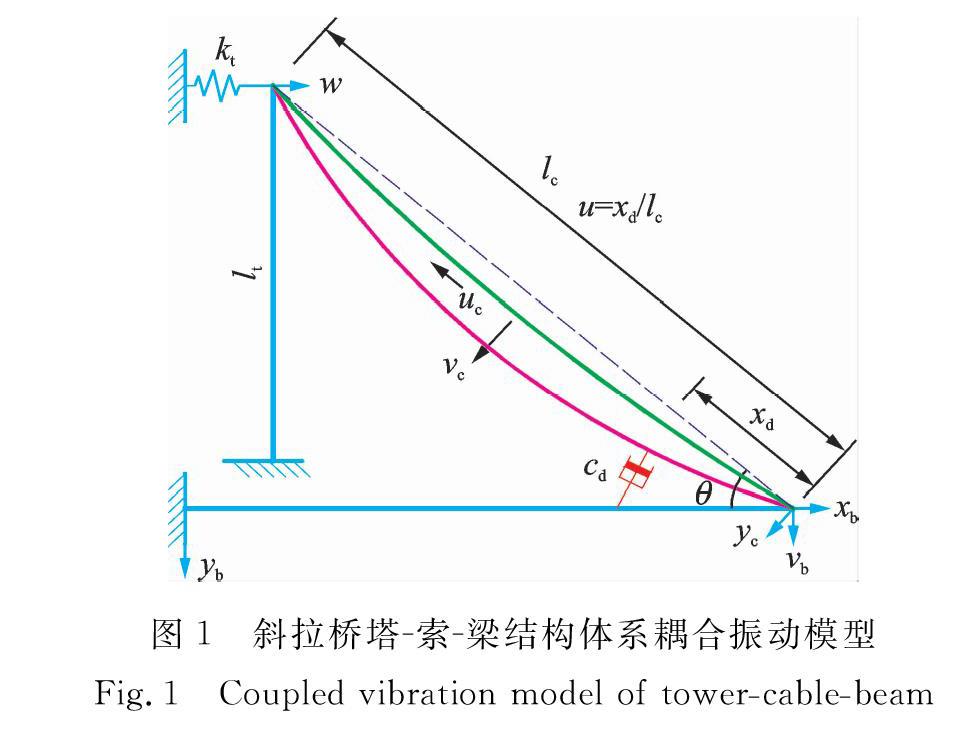
为了突出问题本质，作如下假设：（1）拉索自重沿索长均匀分布，忽略重力垂度以及热胀冷缩引起的拉索质量重分布;（2）拉索本构关系符合胡克定律，忽略拉索抗弯刚度、抗扭刚度和抗剪刚度的影响;（3）阻尼器为线性黏滞阻尼器。考虑桥塔和加劲梁的协同振动影响，建立设置黏滞阻尼器的斜拉桥拉索一塔梁耦合体系的振动模型，如图1所示。

现代大跨度斜拉桥多采用密索体系，桥塔高度已达数百米，并受到多根拉索约束，塔梁结合处常采取固结方式来减小桥塔的内力和加劲梁的轴向拉力。因此，将桥塔视为一端固结，另一端与拉索铰接的Bernoulli-Euler梁。为了考虑其他拉索对桥塔的扶正作用，用刚度为kt的弹簧作为桥塔顶端的外力边界，并假定塔顶横向位移为W（t）。桥梁在地震、风荷载以及车辆荷载等作用时，加劲梁会将这些荷载传递至索塔，再通过索塔传至地基，加劲梁在斜拉索的各点支承作用下，像多跨弹性支承的连续梁，在外激励下易产生竖向位移。因此，将加劲梁视为Bernoulli-Euler梁，一端固结边界，另一端与拉索铰接，其竖向振动位移为ub。拉索与桥塔、加劲梁铰接，uc和ue分别为拉索的纵向和横向的振动位移。黏滞阻尼器的两端分别与拉索、加劲梁连接，它到索梁锚固点的距离为xd，阻尼系数为Cd，安装位置参数u=xd/ιc。各构件参数定义如表1所示。

1.2 设置阻尼器的斜拉索振动控制方程

为计入拉索重力弦向分力的影响，设定斜拉索静态线形为高精度抛物线，其线形方程为

式中 ye为拉索垂度，H为索力水平分力。

基于达朗贝尔原理，拉索做横向振动时面内运动微分方程为 式中 h为斜拉索动张力的水平分力，d为拉索的跨中垂度，δ为狄克拉函数，Fd为黏滞阻尼器的阻尼力，其大小为阻尼系数乘以拉索运动速度，表达式为：Fd （t） =Cd uc（xd，t）。 限于篇幅，斜拉索水平动张力h推导过程可参考文献[9]，其表达式如下

研究表明，斜拉索振动时的一阶模态响应占总响应的比例较大[11]。因此，本文仅考虑拉索的一阶振动模态，斜拉索横向振动位移为

式中 拉索振型

，Ve表示拉索跨中横向振幅。由于式（4）包含了桥塔和加劲梁的振动引起的拉索位移，因此耦合振动模型可考慮桥塔和加劲梁的协同作用引起结构体系的动力学效应。

加劲梁简化为Bernoulli-Euler悬臂梁，其运动偏微分方程为 式中 轴向力N=（H+h）cosθ+Fd sinθ，将加劲梁位移ub分离变量，且仅考虑加劲梁一阶振动模态

ub（xb，t）=Vb（t）φb（xb）

（6）式中 加劲梁振型[12-14]为φb（xb）=A1sir（βbxb）+A2 cos（βbxb）+A3 sinh（βbxb）+A4 cosh（βbxb），依据文献[10]可对A1，A2，A3，A4，βb等参数进行计算。

定义桥塔横向位移为ut（z，t）=φt（z）·W（t），其动力运动方程如下式

式中Mt*，Ct*，Kt*，Pt*分别表示桥塔的广义质量、阻尼、刚度和外荷载。

最后采用伽辽金方法，分别对拉索、加劲梁和桥塔的振动方程进行模态截断，可获得桥塔一索一梁耦合体系的振动方程组，为：

由于上述方程组之间存在高次非线性项，使得索梁模型较为复杂，它耦合了桥塔和加劲梁的振动。分别定义桥塔、拉索、加劲梁的固有频率为Wl，w2，w3，则桥塔振动频率：

;拉索振动频率：

;桥面频率：

。黏滞阻尼器给拉索附加的阻尼比如下式所示

附加阻尼比系数会影响斜拉索的抑振效果。当阻尼系数过小时，阻尼器无法有效抑制拉索的振动;当阻尼系数过大时，阻尼器相当于一个固定约束，将长索转换为两根短索自由振动，并不能起到有效地减振耗能作用。因此，存在一个最优的阻尼系数，使阻尼器的控制效果最好。由图1知，u为阻尼器到索梁锚固点的距离Xd与拉索弦向长度ιc的比值。根据文献[7]建议的被动线性黏滞阻尼器对拉索的最优附加模态阻尼比为ξb=0. 5u。结合以往研究[15-16]，将ξb代入式（11）可得最优黏滞阻尼器系数的表达式由式（12）可知，最优黏滞阻尼器系数Cd与拉索本身的材料参数、固有频率以及阻尼器安装位置相关。与传统单索模型推导的阻尼器阻尼系数相比，该模型可考虑桥塔和加劲梁对斜拉索协同振动的影响。

2 拉索参数振动控制分析

2.1 塔梁协同作用对拉索固有频率的影响

通过上述斜拉索的运动方程求解，可得拉索一阶固有频率w2的表达式如下式所示

为了便于对比分析，基于传统单索模型[16-17]，推导拉索一阶固有频率w0，如下式所示式中

对比w2和w0。表达式可知，引入加劲梁、桥塔对斜拉索的协同作用后，斜拉索内力及边界条件发生变化，一阶固有频率出现多个高次非线性项，在某种程度上影响斜拉索的振动特性。为了研究塔梁协同作用对拉索振动的具体影响，取某斜拉桥的一组斜拉索为算例，具体参数如下：斜拉索单位质量mc=80. 72 kg/m，两端锚固点之间的距离ιe=292. 57m，弹性模量Ee=2.1×1011 Pa，截面积Ae=0. 01022 m2，倾角0= 30°，重力加速度g=9.8 m/s2，索力H取值为4×l04_2×l05 N，可得上述两种模型的拉索固有频率与索力关系曲线，如图2所示。

由图2可知，随着斜拉索索力的增大，拉索的固有频率呈现非线性减小趋势。索力在4×l04_2 0×l04 N之间变化时，单索模型的频率w0。明显大于耦合模型频率w2，两者最大比值可达1.57。但随着索力的增大，斜拉索逐渐张紧，w0与w2曲线的差值逐渐减小，最后趋于重合，塔梁协同作用对张紧拉索的固有频率影响变小。

保持索力H=20×l04 N不变，改变索长ιe值，可得两种模型的拉索固有频率与索长的关系曲线，如图3所示。

由图3可知，随着索长增加，拉索固有频率同样呈现非线性减小趋势。索力为2 0×l04 N的拉索，索长在25-400 m之间变化时，单索模型的频率w0大于耦合模型的频率w2，且随着索长的增大，w0与w2的差值也逐渐增大。说明塔梁的协同作用对长索的影响较大，两者最大比值为1. 02。与索力相比，索长对拉索固有频率的影响较小。

对部分斜拉索而言，单索模型精度与本文的耦合模型相当。但在研究超长斜拉索的振动时，把所有拉索简化为单索模型无法反映拉索的真实情况。与单索模型对比，表2给出了不同长度的斜拉索在不同索力下，塔梁协同作用对固有频率的影响水平。

由表2可知，拉索索长为50 m，索力为40 kN时，塔梁协同作用对拉索固有频率的影响率为-0. 87%，当索长增加到250 m时，影响水平变为-24.77%。但索力增大到200 kN时，其影响水平降低为-0. 03%。由此可见，斜拉索越长，索力越小时，塔梁协同作用的影响愈加明显。而索长越短，索力越大时，塔梁协同作用的影响越弱。因此，斜拉索抑振设计时建议考虑塔梁协同作用的影响。

2.2 黏滞阻尼器的控制效果分析

采用四阶龙格库塔法，编制程序分析斜拉索受控前后的拉索振动位移特征，研究阻尼器的阻尼系数、安装位置、对拉索参数振动的影响。拉索计算参数如表3所示。

由表3参数可计算桥塔、斜拉索和加劲梁的一阶固有频率分别为：w1=19.2 rad/s，w2=8. 864rad/s，w3 =19.2 rad/s。为了研究阻尼器一斜拉索一塔梁结构体系在w1：w2：w3 =2：1：2的频率比下，安装阻尼器前后的斜拉索位移变化，桥塔、拉索和加劲梁的初始位移均为0. Ol m。斜拉索位移时程如图4所示。

由图4（a）可知，斜拉索处于未安装阻尼器的无控状态时，拉索由初始位置开始振动，其振幅逐渐增大，在较短时间内达到响应峰值，幅值为1.19 m，到500 s时拉索振动趋于稳定，振幅几乎没有衰减。由图4（b）可知，斜拉索安装了黏滞阻尼器后，变成有控状态，拉索同样在较短时间内达到响应峰值1. 19m，但随着时间的推移，拉索振幅衰减明显，到500 s时，振幅降为0. 728 m。

拉索发生参数振动时，由于附加阻尼力的存在，其振动幅值逐渐衰减。为了更进一步揭示黏滞阻尼器的抑振效果，引入振幅衰减率λ，其计算公式为式中 A为某时刻未安装阻尼器的无控斜拉索最大振幅，Ao表示有控状态时斜拉索的最大振幅。利用公式（15）可计算受控的斜拉索在500 s时振幅衰减率约为39%。

2.3 黏滞阻尼器阻尼系数的影响

工程实践中，考虑阻尼器安装可行性和桥梁景观性，黏滞阻尼器的安装位置一般靠近索梁锚固端。取安装位置参数u=. Ol，通过改变表3中塔、梁结构参数以及黏滞阻尼系数Cd的取值，可获得索梁频率比分别为1：2，1：1，1：0.5的3种典型参数振动匹配关系，分析阻尼系数对斜拉索的振动影响。不同频率比时，黏滞阻尼器系数与拉索振幅、衰减率的关系曲线如图5所示。

由图5（a）可知，在3种典型索梁频率比时，随着阻尼系数的增大，斜拉索最大振幅均呈轻微的非线性衰减趋势，且衰减过程较慢。由图5（b）可知，随着阻尼系数的增大，拉索振幅衰减率呈现先增大后减小的趋势。振幅衰减率明显存在一个峰值，即有一个临界最优阻尼系数Cd'。当拉索阻尼系数CdCd'时，随着阻尼系数的增大，虽然拉索振幅持续减小，但是振幅衰减率呈现缓慢减小的趋势，且阻尼器的控制效果并没有明显提高。因此，建议阻尼系数设计取值在某一合理范围内，既能满足经济、技术性，也能达到最大的控制效果。

同时，不同频率比下拉索的临界阻尼系数并不相同。当索梁频率比为1：2和1：0.5时，阻尼系数在2×l05-3×l05 N·s/m时的控制效果最佳，而当索梁频率比为1：1时，阻尼系数取值为8×l05-1.1×l06 N·s/m时，拉索振幅的控制效果最佳。为了最大限度地控制拉索在不同频率比下的振动，阻尼器的阻尼系数应取上述较大值8×l05-1.1×106 N·s/m。而由式（12）可得，最优阻尼系数为1. 06×l06 N·s/m，与分析结果吻合较好。因此，黏滞阻尼器的最优阻尼系数公式考虑了桥塔、加劲梁与斜拉索的协同振动影响，同时计算方法准确便捷，工程人员可根据实际情况估算阻尼器阻尼系数。

2.4 黏滞阻尼器安装位置影响

为了研究阻尼器的安装位置u对拉索振幅和振幅衰减率的影响，阻尼器的阻尼系数取值1. 06×106 N·s/m。不同阻尼器位置参数u与最大振幅、衰减率的关系，如图6所示。

由图6可知，随着阻尼器安装位置参数u的增大，即阻尼器位置逐渐靠近斜拉索跨中，远离索梁锚固端时，拉索最大振幅和500 s時振幅衰减率呈非线性减小趋势。阻尼器距离索梁锚固端越远，拉索的最大振幅越小，但振幅衰减率也越小。系统存在一个衰减率为零的临界安装位置u'，当安装位置u>u'时，拉索的振幅衰减率降至负值，此时拉索的振幅随着时间的推移有升高的趋势。斜拉索在不同频率比时，阻尼器的临界安装位置并不相同，索梁频率比为1：0.5的超谐波共振时的u'值最大，1：1的主参数共振次之，1：2的主参数共振时的u'值最小。因此，为了有效控制拉索不同模式的振动，建议黏滞阻尼器的安装位置u不宜超过0. 05。

有趣的是，当阻尼器的安装位移在[O O.04]之间，频率比为2：1：1和2：1：2时，斜拉索振幅衰减曲线较为近似，表明阻尼器对两种共振的振幅抑制效果相近。分析其原因是频率比为2：1：2下，斜拉索发生主参数共振，当频率比为2：1：1时，拉索会发生主共振，都属于亚谐波共振，其振动形式机理具有一定的相似性。这两种共振模式下斜拉索都符合“拍”形特征，但是最大振幅不同。而频率比2：1：0.5时，斜拉索的振动属于超谐波共振，其振幅衰减率大于亚谐波共振。

3 结 论

本文建立了阻尼器一斜拉索一塔梁组合结构体系的耦合参数振动模型，分析了塔梁协同作用对拉索固有频率的影响水平，比较了斜拉索受控前后的拉索振动位移特征，研究了黏滞阻尼器的阻尼系数、安装位置对拉索参数振动的影响，得到如下结论：

（1）塔梁协同作用对斜拉索固有频率的影响与拉索索力、索长密切相关。斜拉索越长，索力越小，塔梁协同作用的影响越强。反之，其影响越弱。斜拉索抑振设计中，建议考虑塔梁协同作用的影响。

（2）相比于未设置黏滞阻尼器的斜拉索，设置黏滞阻尼器的斜拉索的最大振幅更小，且振幅呈明显的非线性衰减，黏滞阻尼器可有效抑制斜拉索的参数振动。

（3）随着阻尼系数的增大，拉索的振幅衰减率呈先增大后趋于减小的趋势。黏滞阻尼器存在一个临界最优阻尼系数Cd'，当阻尼器的阻尼系数超过临界阻尼后，斜拉索的振幅衰减率呈减小趋势，抑振效果的提高并不明显。工程实际时，在满足经济性、技术性的同时，阻尼器的阻尼系数应控制在某一合理范围内。

（4）阻尼器安装位置距离索梁锚固端的距离越大，拉索最大振幅和振幅衰减率越小。黏滞阻尼器也存在一个衰减率为零的临界安装位置u'，当安装位置超过u'后，斜拉索的振幅衰减率为负值，抑振效果较差。在工程实际中，建议黏滞阻尼器的安装位置u不宜超过0. 05。

（5）考虑斜拉桥、桥塔和加劲梁三者协同振动，黏滞阻尼器一拉索一梁结构体系的最优阻尼系数的计算方法准确便捷，工程人员可以根据实际情况计算黏滞阻尼器需要满足的阻尼系数。

参考文献：

[1] Wu Q， Takahashi K， Nakamura S. Non-linear re-sponse of cables subjected to periodic support excita-tion considering cable loosening[J]. Journal of Soundand Vibration，2004，27（1/2）：453-463.

[2] Lilien J L， Pinto Da Costa A. Vibration amplitudescaused by parametric excitation of cable stayed struc-tures[J]. Journal of Sound and Vibration，1994，174（1）：69-90.

[3] Yamaguchi H， Fujino Y. Stayed Cable Dynamics andIts Vibration Control[M]. Bridge Aerodynamics，Balkema Rotterdam，The Netherlands，1998： 235-253.

[4] 巫生平，张 超，房贞政，斜拉桥黏滞阻尼器设计方案及参数回归分析[J].桥梁建设，2014，44（05）：21-26.

Wu Shengping， Zhang Chao， Fang Zhenzheng. Designschemes and parameter regression analysis of viscousdampers for cable-stayed bridge[J]. Bridge Construc-tion，2014，44（05）：21-26.

[5] 周海俊，丁 炜，孙利民，拉索一阻尼器一弹簧系统的阻尼特性分析[J].工程力学，2014，31（01）：79-84.

Zhou Haijun，Ding Wei，Sun Li-min. Damping of tautcable with a damper and spring[J]. Engineering Me-chanics，2014，31（01）：79-84.

[6] 段元锋，李 频，周仙通，等，斜拉索外置式黏滞阻尼器实用设计方法[J].中国公路学报，2015，（11）：46-511+59.

Duan Yuanfeng， Li Pin， Zhou Xiantong， et al. Practi-cal design method for external viscous damper of staycable[ J]. China Journal of Highway and Transport，2015，（11）：46-51-1- 59.

[7] 陳文礼，李 惠，黏滞阻尼器对拉索参数振动的控制分析[J].地震工程与工程振动，2007，（02）：137-144.

Chen Wenli， Li Hui. Passive control for parametric vi-bration of cables using viscous fluid dampers[J].Earthquake Engineering Vibration， 2007， （02）： 137-144.

[8] 垄 平，苏潇阳，蔡向阳，等，拉索对斜拉桥竖向频率的影响研究[J].振动工程学报，2018，31（6）：957-965.

GONG Ping，SU Xiaoyang，CAI Xiangyang，et al. Theinfluence of cables on vertical frequency of cable-stayedbridge[J]. Journal of Vibration Engineering，2018，31（6）：957-965.

[9] 汪 峰，陈福清，文晓旭，等，考虑温度影响的斜拉索参数振动模型及响应分析[J].重庆交通大学学报（自然科学版），2016，35（2）：1-6.

Wang Feng， Chen Fuqing， Wen Xiaoxu， et al. Analy-SiS of cable parametric vibration model and responsewith consideration of temperature effect[J]. Journal ofChongqing Jiaotong University （Natural Science），2016.35（2）： 1-6.

[10]汪 峰，文晓旭，刘章军，斜拉桥塔一索一梁耦合参数振动模型及响应分析[J].固体力学学报，2015，36 （5）：446-452.

Wang Feng， Wen Xiaoxu， Liu Zhangjun. Coupled vi-bration model for tower-cable-deck of long-span cable-stayed bridge and its response analysis[J]. ChineseJournal of Solid Mechanics，2015，36（5）：446-452.

[11]杨咏漪，陈克坚，大跨度铁路斜拉桥斜拉索参数振动分析[J].铁道工程学报，2012 ，169 （10）：60-65.

Yang Yongyi， Chen Kejian. Research on parametricoscillation of cables for long span railway cable-stayedbridge[J]. Journal of Railway Engineering Society，2012， 169（10）： 60-65.

[12]康厚军，赵跃宇，蒋丽忠，参数振动和强迫振动激励下超长拉索的面内非线性振动[J].中南大学学报（自然科学版），2011，42（8）：2439-2445.

Kang Houjun， Zhao Yueyu， Jiang Lizhong. In- planenonlinear vibration of super long stay cables under par-ametric and forced excitations[J]. Journal of CentralSouth University （Science and Technology），2011，42（8）： 2439-2445.

[13] Wang T M， Nettleton R H， Keita B.Natural frequen-cies for out-of-plane vibrations of continuous curvedbeams[J]. Journal of Sound and Vibration，1980， 68（3）： 427-436

[14] Gattulli V， Martinelli L， Perotti F， et al. Nonlinearoscillations of cables under harmonic loading using an-alytical and finite element models[J]. Computer Meth-ods in Applied Mechanics and Engineering， 2004， 193（1/2）：69-85

[15] Pacheco B M， Fujino Y， Sulekh A. Estimation curvefor modal damping in stay cables with viscous damper[J]. Journal of Structural Engineering，1993，119 （6）：1961-1978.

[16]陈丕华，大跨斜拉桥拉索的参数振动及其控制[D].长沙：湖南大学，2009.

Chen Pihua. Parametric vibration of cable and its con-trol in long-span cable-stayed bridge[D]. Changsha：Hunan University，2009.

[17]王 波，大跨斜拉桥拉索局部振动特性及其影响研究[D].武汉：华中科技大学，2008.

Wang Bo. Characteristic and influence of local cable vi-bration on long-span cable-stayed bridge[D]. Wuhan：Huazhong University of Science and Technology，2008.