Gauge Transformation for BCr-KP Hierarchy and Its Compatibility with Additional Symmetry∗
Lu-Min Geng (耿露敏), Hui-Zhan Chen (陈慧展), Na Li (李娜), and Ji-Peng Cheng (程纪鹏)
School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China
(Received July 1, 2018)
Abstract The BCr-KP hierarchy is an important sub-hierarchy of the KP hierarchy.In this paper, the BCr-KP hierarchy is investigated from three aspects.Firstly, we study the gauge transformation for the BCr-KP hierarchy.Different from the KP hierarchy, the gauge transformation must keep the constraint of the BCr-KP hierarchy.Secondly,we study the gauge transformation for the constrained BCr-KP hierarchy.In this case, the constraints of the Lax operator must be invariant under the gauge transformation.At last, the compatibility between the additional symmetry and the gauge transformation for the BCr-KP hierarchy is explored.
Key words: the BCr-KP hierarchy, gauge transformation, additional symmetry
1 Introduction
The Kadomtsev-Petviashvili (KP in short)hierarchy[1−2]is an important research area in the integrable systems.There is a kind of sub-hierarchy of the KP hierarchy studied by Dateet al.in Ref.[3], which can be viewed as the generalization of the BKP and CKP hierarchies.[1,3−5]In Ref.[4],Zuoet al.made a slight modification for the sub-KP hierarchy of Ref.[3], and called it theBCr-KP hierarchy, to ensure its consistence with the CKP and BKP hierarchy in the case ofr=0 andr=1 respectively.In Ref.[4], Zuoet al.not only constructed the additional symmetries of theBCr-KP hierarchy and its constrained case, but also showed that the corresponding additional symmetries form a-algebra and a Witt algebra respectively.In this paper, we will consider the gauge transformations and its relation with the additional symmetry of theBCr-KP hierarchy.
The gauge transformation[6−8]is an efficient way to construct solutions for integrable hierarchies.Its initial ideal dates back to the gauge equivalence with the different integrable models.The gauge transformation operators of the KP hierarchy[6−7]mainly included the differential typeTDand the integral typeTI.Now, the gauge transformations of many important integrable hierarchies have been constructed.For instance, the KP and modified KP hierarchies,[6−11]the BKP and CKP hierarchies,[12−14]theq-KP and modifiedq-KP hierarchies,[15−18]the discrete KP and modified discrete KP hierarchies.[19−21]In this paper, we focus on the gauge transformation operators of theBCr-KP hierarchy and its constrained case.Different from the KP hierarchy, the gauge transformations of theBCr-KP hierarchy must keep theBCr-constraint invariant, besides keeping the Lax equation.It is found in this paper that the combination ofTDandTIis the suitable choice of the gauge transformation for theBCr-KP hierarchy.As for the constrained case, the corresponding gauge transformations have to ensure the constrained form of the Lax operator unchanged,besides the two conditions in unconstrained case.In fact, this can be done, by choosing the eigenfunction in the negative part of the Lax operator as the generating function in the gauge transformation operators.What is more, the successive applications of the corresponding gauge transformation operators are considered in this paper.
Another topic in this paper is the additional symmetry.[1−2,22−24]The additional symmetries are from thew∞algebra[24]or the so-called centerlessW1+∞-algebra,which are an exceptional kind of symmetries relying explicitly on the space and time variables.[25−28]Nowdays, there are many important results on the additional symmetries.[4,29−35]In this paper, we will study the compatibility of the additional symmetries and the gauge transformation for theBCr-KP hierarchy.It is an interesting question to discuss the changes of the additional symmetries under the gauge transformations.For theBCr-KP hierarchy after the gauge transformation,we find that the additional symmetries remain the ones, which shows some compatibilities of the additional symmetry and the gauge transformation.
The organization of this paper is as follows.In Sec.2,some backgrounds of theBCr-KP hierarchy are introduced.In Sec.3, the gauge transformations for theBCr-KP hierarchy are given to keep theBCr-constraint.In Sec.4,the gauge transformation for the constrainedBCr-KP hierarchy on the Lax operator are investigated.In Sec.5, we focus on the compatibility of the gauge transformations and the additional symmetries.
2 Background on the BCr-KP Hierarchy
In this section, we will review the backgrounds on theBCr-KP hierarchy,[4]based upon the pseudo-differental operators.The multiplication of∂iwith thefobeys the Leibnitz rule[2]
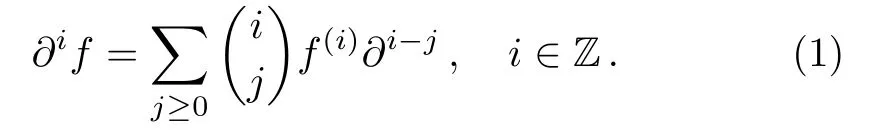
Forwe denoteandA−=What is more,AforA·fmeans that the multiplication ofAandf, whileA(f)denotes the action ofAonf.The conjugate operation∗obeys the following rules: (AB)∗=B∗A∗,∂∗=−∂,f∗=f, for any pseudo-differential operatorsAandBand any functionf.
Let us introduce the KP hierarchy[1−2]firstly, sinceBCr-KP hierarchy is a kind of sub-hierarchy of the KP hierarchy.The Lax equation of the KP hierarchy is defined by

Here the Lax operator is given by
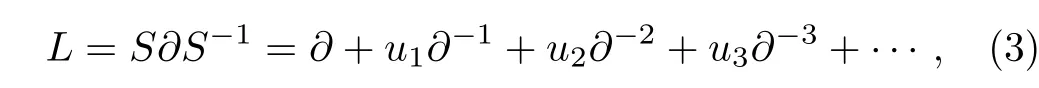
andS= 1 +s1∂−1+s2∂−2+s3∂−3+···is called the dressing operator.And the coefficientss1,s2,s3,...are the functions of infinitely many variablest= (t1=x,t2,t3,...).The Lax equation (2)is equivalent to the Sato’s equation:

The eigenfunctionϕand the adjoint eigenfunctionψof the KP hierarchy are defined by

respectively.
Next introduce
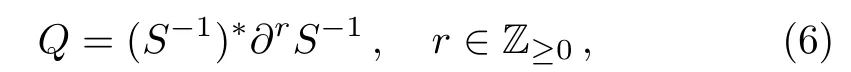
whereSis the dressing operator of the KP hierarchy.Generally, theBCr-KP hierarchy[3−4]can be defined by imposing the condition below on the dressing operatorS,

which means thatQis anr-order differential operator satisfyingQ∗= (−1)rQ.Further according to Eqs.(3)and(4), one can find
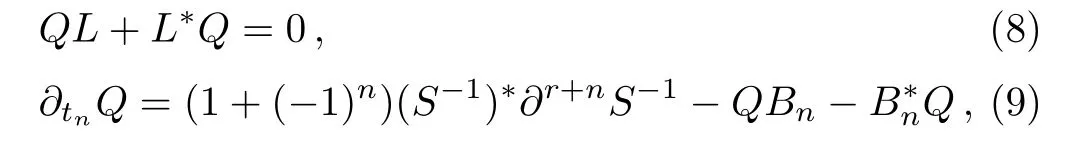
and by talking the negative part and usingQ=Q+, one gets 1 + (−1)n= 0.Therefore, theBCr-KP hierarchy only has odd flows.
By summarizing the results above, theBCr-KP hierarchy is defined by
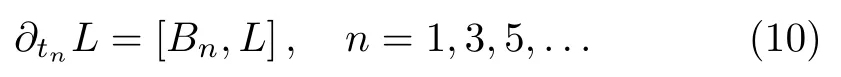
and the Lax operatorLin Eq.(3)has the reduction condition (7)or (8).Notice that
(i)BC0-KP is the CKP hierarchy.Whenr= 0, one can findQ=1 andL∗=−L.
(ii)BC1-KP is the BKP hierarchy.Whenr= 1, one can findQ=∂andL∗=−∂L∂−1.
According to Eqs.(5)and (8), it can be found that the adjoint eigenfunction of theBCr-KP hierarchy can be expressed byQ(ϕ), whereϕis an eigenfunction.The constrainedBCr-KP hierarchy[4]is defined by imposing the below constraints on the Lax operator ofBCr-KP hierarchy
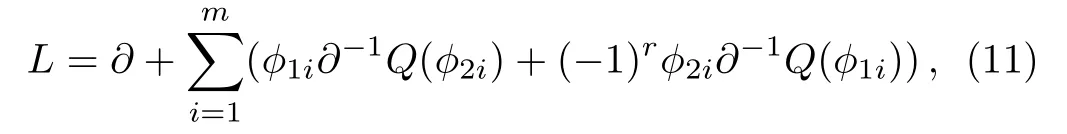
whereϕ1iandϕ2iare two eigenfunctions of theBCr-KP hierarchy.
3 The Gauge Transformation for the BCr-KP Hierarchy
In this section, we will consider the gauge transformation of theBCr-KP hierarchy.
Firstly, let us review the gauge transformation of the KP hierarchy.[6−7]Assume thatTis a pseudo-differential operator andLis the Lax operator of the KP hierarchy.DenoteL(1)=TLT−1andB(1)n ≡(L(1))n+.If∂tnL(1)=[B(1)n ,L(1)]still holds,thenTis called the gauge transformation operator for the KP hierarchy.There are two elementary types of the gauge transformation operator in the KP case.
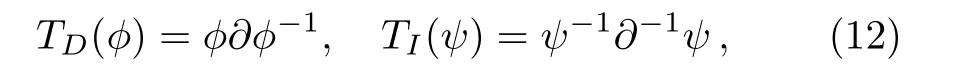
whereϕandψare the eigenfunction and adjoint eigenfunction respectively.
Given eigenfunctionϕiand adjoint eigenfunctionψifori= 1,2,...,n, consider the following chain of the gauge transformation operatorsTD(ϕ)andTI(ψ).
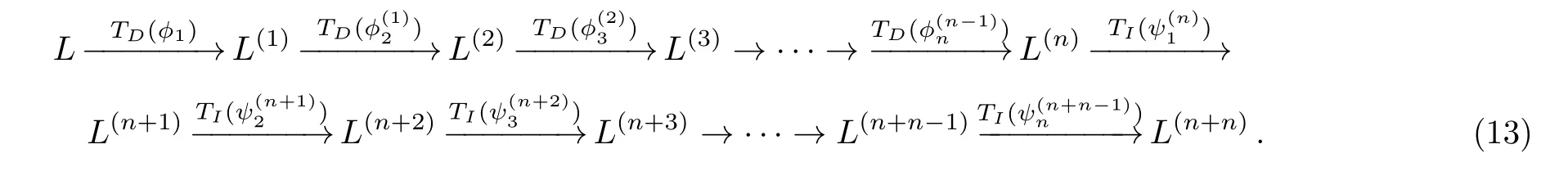
Denote

The next proposition will give the explicit form ofTn+n.For this, the generalized Wronskian determinant[9]will be needed, which is defined by
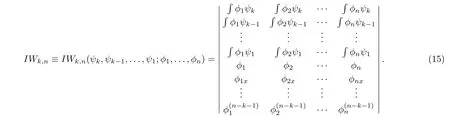
Proposition 1[9]Tn+nandT−1n+nhave the following forms Before further discussing, the next lemma will be needed.
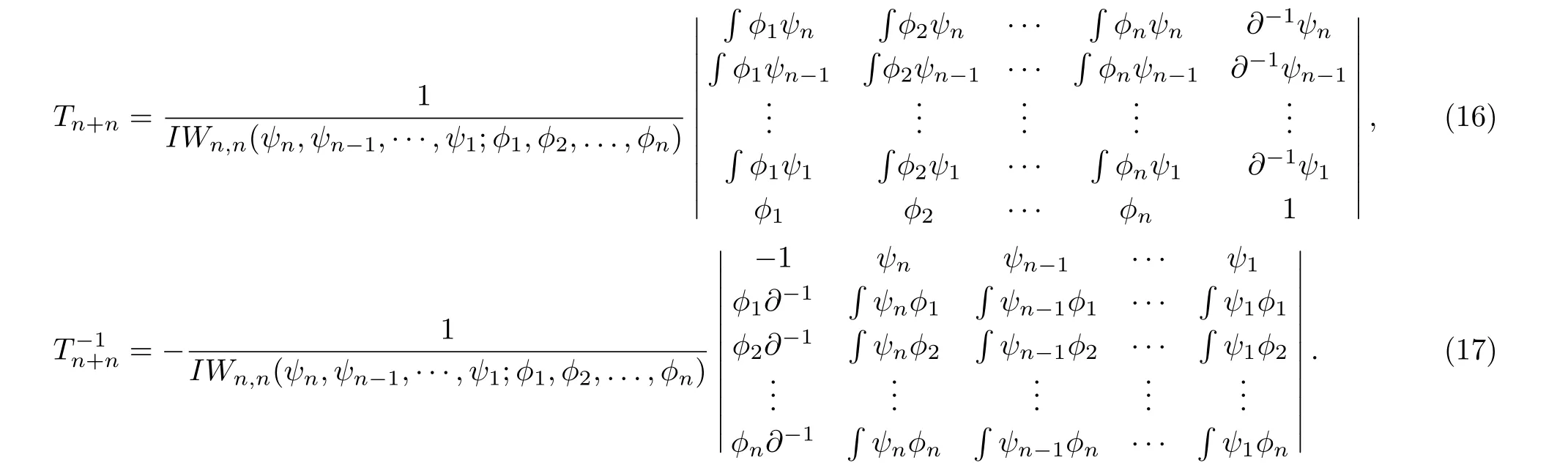
Lemma 1[7,11]For any functionsfand any pseudo differential operator
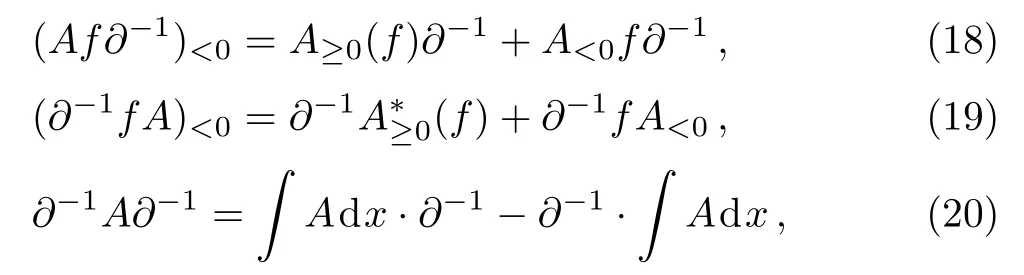
After the above preparation, we begin to consider the gauge transformations of theBCr-KP hierarchy.The gauge transformation operatorTof theBCr-KP hierarchy must satisfy the following two conditions, which are different from the KP hierarchy, that is
(i)Keeping the Lax equation:∂t2n+1= [2n+1,],where=TLT−1and2n+1≡()2n+1+.
(ii)Keeping theBCr-constraint:= ()+, where=(T−1)∗QT−1.
However in theBCr-KP hierarchy, singleTDorTIcan not ensure theBCr-constraint invariant.Fortunately,it is found that the combination ofTDandTI, i.e.,T1+1=TI((Q(ϕ))(1))TD(ϕ), can satisfy the two conditions above.We will show this fact below.
Proposition 2 T1+1=TI((Q(ϕ))(1))TD(ϕ)is the gauge transformation of theBCr-KP hierarchy, whereϕis the eigenfunctionThat is to say,
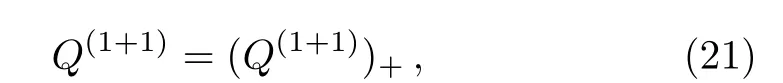
ProofFirstly by using (ϕQ(ϕ)dx)· ∂=∂ ·(∫ϕQ(ϕ)dx)−ϕQ(ϕ),
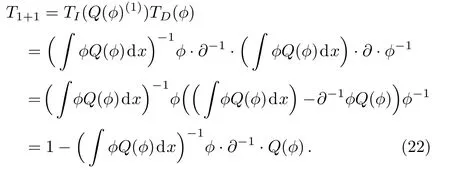
Similarly
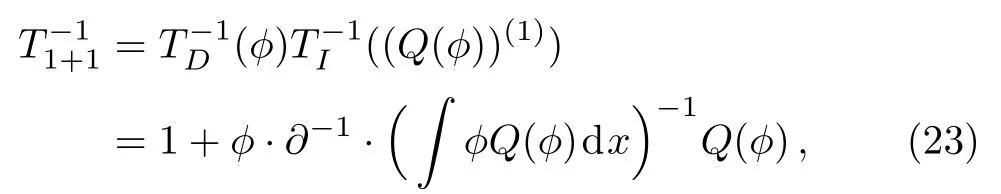
therefore
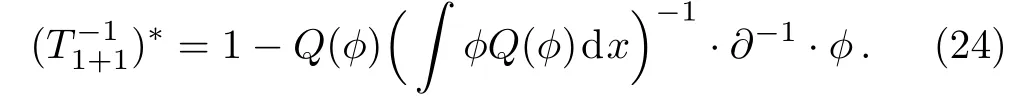
Then according to Eqs.(22), (24)and Lemma 1,

Further according to Lemma 1

By subsituting Eq.(26)into Eq.(25)and using the relationQ∗=(−1)rQ, one can at last obtain Eq.(21).□
Remark 1The results in Proposition 3 contain the gauge transformation operators of the CKP and BKP hierarchies:[12−14]
(i)The CKP hierarchy:T1+1=1−(∂−1x ϕ2)−1ϕ∂ϕ.
(ii)The BKP hierarchy:T1+1=1−2ϕ−1∂−1ϕx.
Remark 2In generalQ1+1≠ Q, thoughQ1+1=Q,whenr=0 orr=1.
4 The Gauge Transformation for the Constrained BCr-KP Hierarchy
In this section, we will consider the gauge tranformation of the constrainedBCr-KP hierarchy.Before doing this, let us review some results on the gauge transformations of the constrained KP hierarchy first.
Proposition 3[10,13]For the constrained KP hierarchy
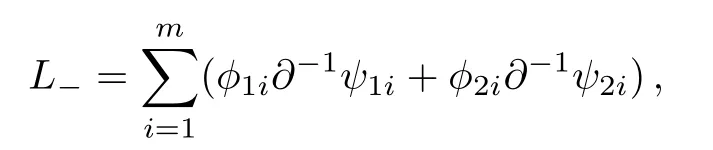
under the gauge transformationwe have
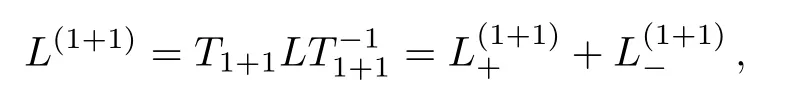
where


Here
As for the case of theBCr-KP hierarchyL=the corresponding gauge transformation operatorThas to satisfy the following conditions:
(i)Keeping the Lax equation:whereand
(ii)Keeping theBCr-KP constraint:where
(iii)Keeping the form of Lax operator:
The required gauge tranformation operatorTis given in the next proposition.
Proposition 4For the constrainedBCr-KP hierarchy
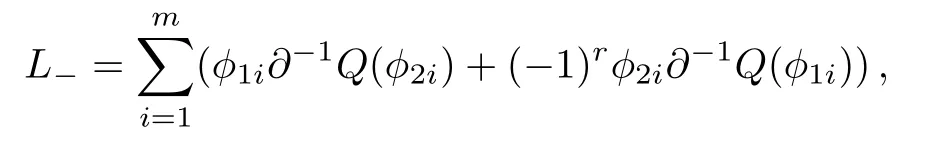
the gauge transformation operator is given byT1+1=TI((Q(ϕ11))(1))TD(ϕ11).Under the gauge transformationT1+1, the Lax operatorLwill become into
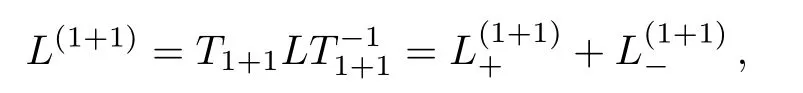
where
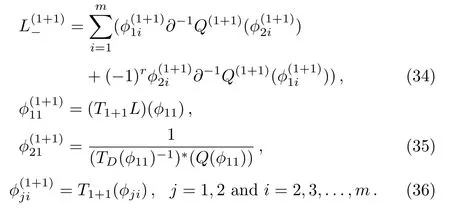
ProofIn order to proveT1+1is the gauge transformation of the constrainedBCr-KP hierarchy, we only need to show


wherei=1,2,...,m.
Wheni=1, according to Proposition 3,
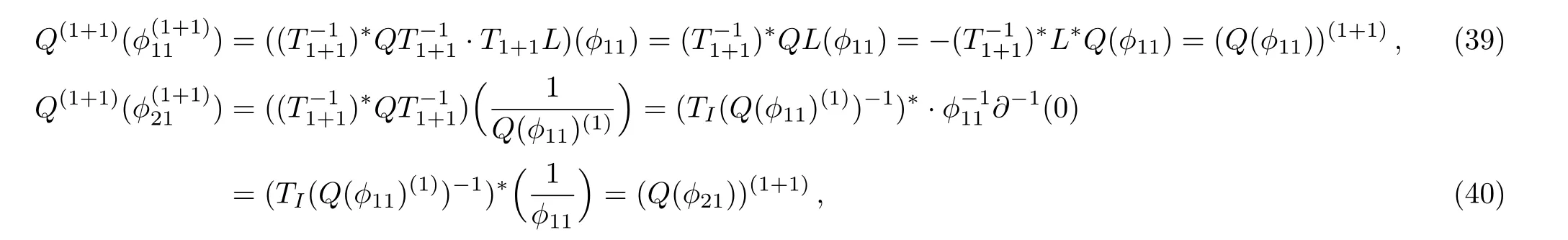
where we have usedtheBCr-KP constraint (8)and
Fori≠1 andj=1,2,
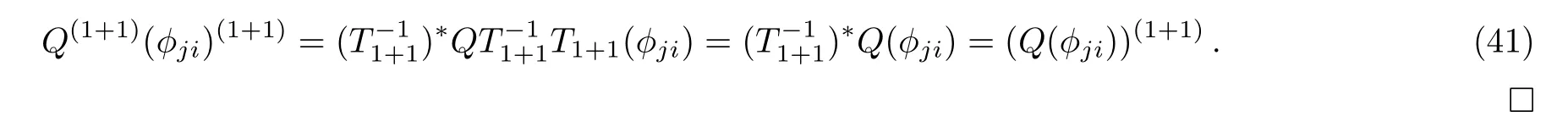
According to Proposition 1 and 4, we can know that
Proposition 5For the constrainedBCr-KP hierarchyundern-step gauge transformationsTn+n, we have
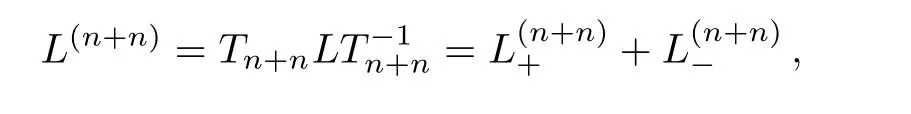
where

Remark 3Whenr= 0 andr= 1, the corresponding results in Proposition 5 are consistent with the cases in Ref.[13].
5 The Additional Symmetry and the Gauge Transformation for the BCr-KP Hierarchy
In this section, we will discuss the compatibility of the additional symmetry and the gauge transformation operators for theBCr-KP hierarchy.
At first,additional symmetries for theBCr-KP hierarchy[4]will be introduced.Denote
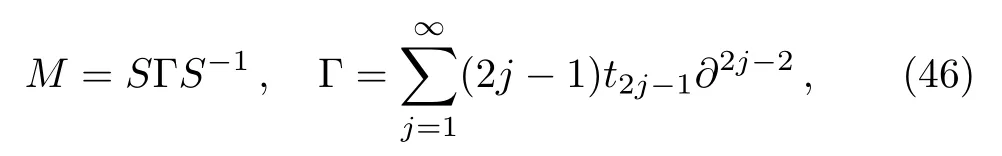
which satisfies∂t2j−1M= [B2j−1,M] and [L,M]= 1.And let
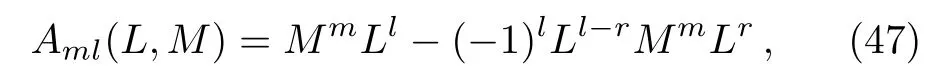
satisfying

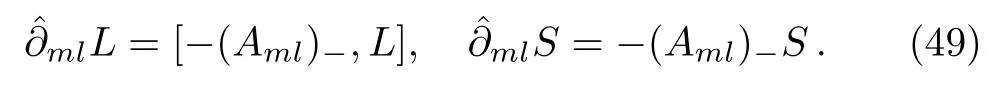
Some lemmas will be needed when we consider the additional symmetries under the gauge transformations for theBCr-KP hierarchy.
Lemma 2For the eigenfunctionϕof theBCr-KP hierarchy
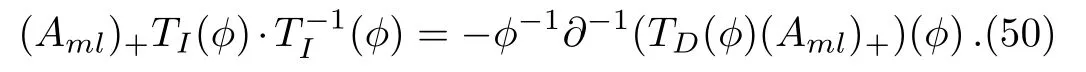
ProofBy the following direct computations

Lemma 3For the eigenfunctionϕof theBCr-KP hierarchy
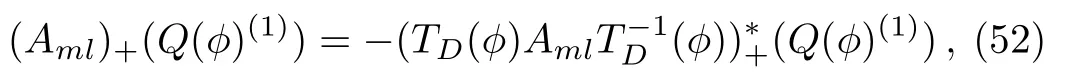
whereQ(ϕ)(1)=−(T−1D(ϕ))∗(Q(ϕ))=TI(ϕ)(Q(ϕ)).
ProofAccording to Eqs.(18), (48), and (50)

Therefore

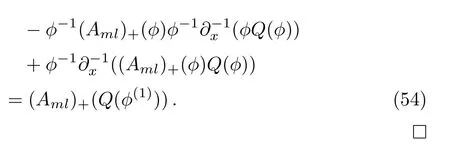
With these preparations, we can get the following results.
Proposition 6For theBCr-KP hierarchy,the additional symmetry flows can commute with the gauge transformationsT1+1=TI(Q(ϕ)(1))TD(ϕ), that is
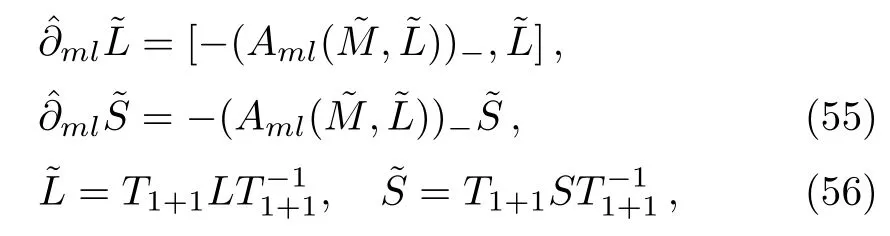
if and only if the eigenfunctionϕtransforms under the additional symmetries in the following way
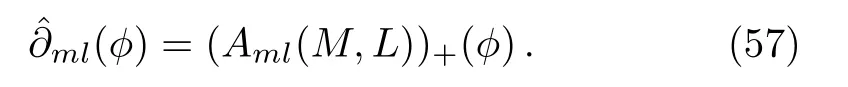
ProofFirstly, according to Eq.(49)
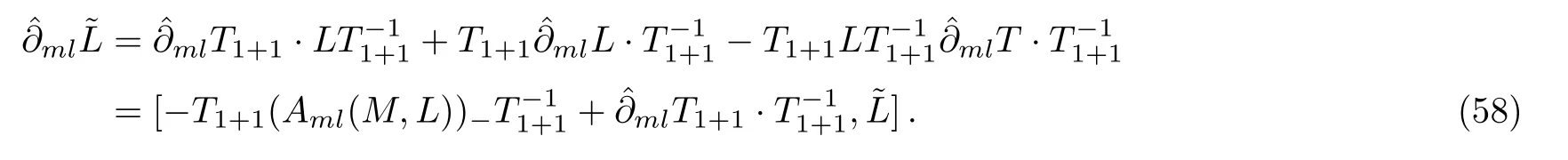
On the other hand
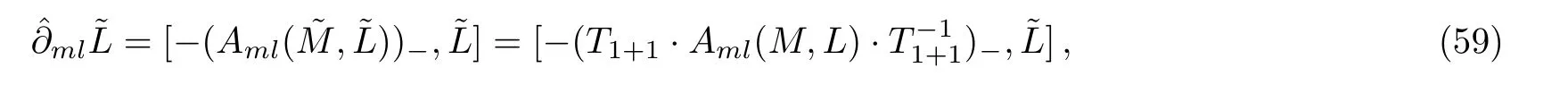
thus Eq.(55)holds, which means

By Eqs.(18), (19), and (52)

According to Eqs.(61), (62), Eq.(60)is true if and only if

 Communications in Theoretical Physics2019年3期
Communications in Theoretical Physics2019年3期
- Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1−xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects∗
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
