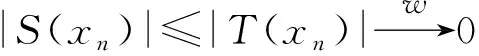序几乎(L)-Dunford-Pettis算子

梅礼华， 陈滋利

(1. 兰州财经大学 信息工程学院, 甘肃 兰州 730020; 2. 西南交通大学 数学学院, 四川 成都 611756)

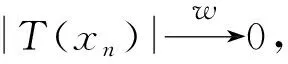
首先根据文献[2]介绍2种重要的集合：

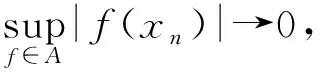
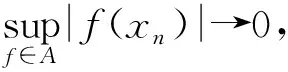
本文中的E′表示Banach格E的拓扑共轭空间，(F′)+表示Banach格F的拓扑共轭空间的正部，即(F′)+：={f∈F′:f≥0}.AL空间是指Banach格E的正部中的向量x和y，x∧y=0满足‖x+y‖=‖x‖+‖y‖，AM空间指Banach格E的正部中的向量x、y，x∧y=0满足‖x∨y‖=max{‖x‖,‖y‖}.L(E,F)表示全体从Banach格E到Banach格F的线性算子，本文所涉及其他的未经解释的Banach格以及正算子理论中的一些概念、符号及术语详见本文文献[3-4].

1 主要结论

定义1.1一个算子T:E→F称为序几乎(L)-Dunford-Pettis算子，如果T′把F′中的序有界集A映成E′中的几乎(L)集，即T′(A)是几乎(L)集.

根据文献[1]中定理1.5可得如下定理.

定理1.2设E和F是2个Banach格，则下列条件等价：

1)T是序几乎(L)-Dunford-Pettis算子.

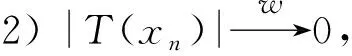
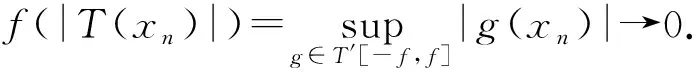
定理1.3设E、F和G是3个Banach格，则:

1) 所有序几乎(L)-Dunford-Pettis算子的全体是L(E,F)的范数闭的向量子空间;

2)T:F→G是序几乎(L)-Dunford-Pettis算子，S:E→F保不交算子，那么T°S是序几乎(L)-Dunford-Pettis算子;

3)T:F→G是序有界算子，S:E→F是序几乎(L)-Dunford-Pettis算子，那么T°S是序几乎(L)-Dunford-Pettis算子.

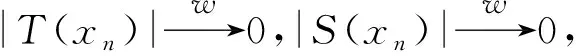
|(S+T)(xn)|≤|S(xn)|+|T(xn)|,

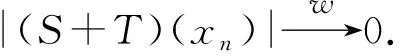
f(|T(xn)|)≤

f(|(T-Tn)(xn)|+|Tn(xn)|)≤

f(|(T-Tn)(xn)|)+f(|Tn(xn)|)≤

‖f‖·‖T-Tn‖·‖xn‖+f(|Tn(xn)|).

而

‖Tn-T‖→0， f(|Tn(xn)|)→0，

所以f(|T(xn)|)→0，即T也是序几乎(L)-Dunford-Pettis算子.

由于T是序几乎(L)-Dunford-Pettis算子，故有

3) 因为T是序有界算子，由文献[5]中的定理1.73有T′是序有界的，∀f∈(G′)+,有T′[-f,f]是序有界集，又因为S是序几乎(L)-Dunford-Pettis算子，则(T°S)′[-f,f]=S′T′[-f,f]是几乎(L)集，所以T°S是序几乎(L)-Dunford-Pettis算子.

定理1.4设E和F是2个Banach格，T:E→F是序几乎(L)-Dunford-Pettis算子，如果F有正的schur性质，那么T是几乎Dunford-Pettis算子.

定理1.5设E和F是2个Banach格，如果下列条件之一成立，那么T:E→F是序几乎(L)-Dunford-Pettis算子.

1)T是序有界的.

2)T是保不交的.

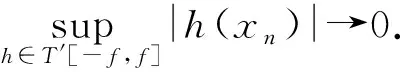
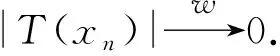
定理1.6设E和F是2个Banach格，如果E是有单位元的AM空间且T:E→F，则下列条件等价：

1)T是序弱紧算子;

2)T是序几乎(L)-Dunford-Pettis算子.

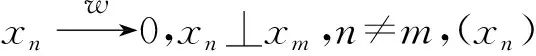
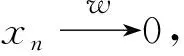
因为T是序几乎(L)-Dunford-Pettis算子，那么

故得‖T(xn)‖→0.

一个算子T:E→X称为AM紧算子，如果对任意的x∈E+,有T[-x,x]是X中的相对紧集，根据定理1.6和文献[6]中的性质2.7得到下面推论.

推论1.7设E和F是2个Banach格，T:E→F是序几乎(L)-Dunford-Pettis算子，如果Banach格E′是离散的，那么T是AM紧算子.

由于(L)集是几乎(L)集，但是几乎(L)集不一定是(L)集，例如L1[0,1]的闭单位球BL1[0,1]是几乎(L)集，但不是(L)集，所以序(L)-Dunford-Pettis算子是序几乎(L)-Dunford-Pettis算子，但是序几乎(L)-Dunford-Pettis算子不一定是序(L)-Dunford-Pettis算子，就有下面的定理.

定理1.8设E和F是2个Banach格，T:E→F是序几乎(L)-Dunford-Pettis算子，如果Banach格E的格运算是弱序列连续的，那么T是序(L)-Dunford-Pettis算子.

证明设A是F′中的序有界集，因为T是序几乎(L)-Dunford-Pettis算子，那么T′(A)是几乎(L)集，考虑算子

S:E→l1,S(x)=fn(x),

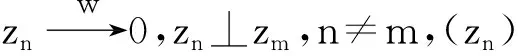
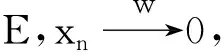
|fn(xn)|=|S(xn)|≤‖S(xn)‖→0.

根据文献[2]中的定理1.1可得T′(A)是(L)集，所以T是序(L)-Dunford-Pettis算子.

定理1.9设E和F是2个Banach格，0≤S≤T,T:E→F是序几乎(L)-Dunford-Pettis算子，那么S是序几乎(L)-Dunford-Pettis算子.