分振幅型全Stokes同时偏振成像系统波片相位延迟误差分析*
殷玉龙 孙晓兵 宋茂新 陈卫 陈斐楠
1) (中国科学院安徽光学精密机械研究所, 合肥 230031)
2) (中国科学技术大学, 合肥 230026)
3) (中国科学院通用光学定标与表征技术重点实验室, 合肥 230031)
(2018 年8 月18日收到; 2018 年10 月20日收到修改稿)
分振幅型全Stokes同时偏振成像仪具有实时性好、空间分辨率高、精度高等优点, 有很高的应用价值.分振幅型全Stokes同时偏振成像系统利用偏振分束器、1/2波片和1/4波片将入射光Stokes矢量调制在4幅图像中, 可解析入射光Stokes矢量. 1/2波片和1/4波片的相位延迟误差对Stokes矢量测量精度有着不可忽略的影响. 建立了包含上述两种误差的Stokes矢量测量误差方程, 分析了1/2波片和1/4波片相位延迟耦合误差对自然光、0°/45°线偏光、左旋圆偏光等典型基态入射光的Stokes矢量测量误差的影响, 推导了任意偏振态的Stokes矢量测量误差的表征方法. 在邦加球球面和球内选取不同偏振度的Stokes矢量作为入射光进行仿真. 结果表明, Stokes矢量测量误差和偏振度测量误差均随着入射光偏振度的增大而增大. 选取入射光偏振度为1时的偏振测量精度评估系统. 为满足2%的偏振测量精度, 1/2波片相位延迟误差应在±1.6°内, 1/4波片相位延迟误差应在±0.5°内. 这对提高系统的偏振测量精度具有重要意义, 为系统设计和研制提供了重要的理论指导.
1 引 言
偏振是光的一种本质属性, 偏振信息不仅包含强度信息还包含偏振度、偏振角和椭圆度角等信息. 光与大气或目标相互作用时会改变光的偏振特性, 光的偏振特性的变化可以表征大气或目标的物理属性, 因此偏振探测广泛用于仿生导航、水下目标探测、天文探测、大气遥感、空间目标3D重建和生物医学等领域[1-6]. 为了实现目标偏振信息的探测, 需要研制高精度的偏振成像系统, 偏振成像系统可分为两类: 分时偏振成像系统和同时偏振成像系统. 分时偏振成像系统中普遍存在转动部件或分时调制器, 导致分时偏振成像系统无法偏振探测快速变化的目标. 为实现动态目标的偏振探测, 同时偏振成像系统的研制已成为研究热点. 1982年,Azzam[7]最先提出一种基于振幅分割的同时偏振成像系统, 该系统利用镀膜分光器和Wollaston棱镜将入射光分为4束光, 由4个探测器实现了对入射光Stokes参数线偏振分量的同时测量. 2008年,Pezzaniti等[8]成功研制了分振幅全Stokes同时偏振成像系统, 利用偏振分束器(polarization beam splitter, PBS)、1/2波片 (half wave plate, HWP)和1/4波片(quarter wave plate, QWP)将入射光分为4束光, 由4个探测器实现对入射光全Stokes参数的同时测量. 2003年, Oka和Kaneko[9]首次提出一种基于双折射楔形棱镜的通道调制型偏振成像仪, 随后国内外学者对基于双折射楔形棱镜的通道调制型偏振成像仪进行了改进[10-12], 提高了基于双折射楔形棱镜的通道调制型偏振成像仪的偏振探测性能. 2016年, 权乃承等[13]提出一种基于孔径分割与视场分割的通道型成像光谱偏振技术,并进行仿真分析验证了该方案的可行性. 2018年,冯斌等[14]研制了分焦平面同时偏振成像仪, 并给出了性能评估模型. 为了提高偏振测量精度, 国内外研究人员针对不同调制原理的同时偏振成像系统进行了系统参数误差分析等方面的工作[15-19].
分振幅型全Stokes同时偏振成像系统没有时间和空间的失调, 具有实时性好、空间分辨率高、精度高等优点, 同时还能实现全Stokes参数的测量, 具有很高的应用价值. 波片是分振幅型全Stokes同时偏振成像系统的核心光学元件, 波片相位延迟误差对系统偏振测量精度有着不可忽略的影响, 为实现自主研制高偏振测量精度的分振幅型全Stokes同时偏振成像系统, 分析系统中波片相位延迟误差对偏振测量精度的影响已成为急需解决的关键问题.
本文介绍了分振幅型全Stokes同时偏振成像系统的工作原理, 建立了包含HWP和QWP相位延迟误差的Stokes矢量测量误差方程; 仿真了HWP和QWP相位延迟误差对自然光、0°/45°线偏光、左旋圆偏光等7种典型基态入射光的Stokes矢量测量误差的影响, 推导了任意入射光Stokes矢量测量误差的表征方法; 利用邦加球(Poincaré sphere)采样法仿真了不同偏振度的Stokes矢量作为入射光时, HWP和QWP相位延迟误差对偏振测量精度的影响, 为保证系统的偏振测量精度在2%内, 给出了波片相位延迟的加工精度要求,这对系统参数设计、原理样机的研制具有重要的指导意义.
2 分振幅型全Stokes同时偏振成像系统原理及误差建模
2.1 偏振成像系统工作原理
分振幅型全Stokes同时偏振成像系统原理如图1所示, 入射光通过光学镜头后, 被部分偏振分束器(partial polarization beam splitter, PPBS)分成两路, 一路是从 PPBS透射的光束, 被HWP调制后由PBS1分离为P偏振光和S偏振光, 从PBS1透射的P偏振光由CCD1接收, 反射的S偏振光由CCD2接收; 另一路是从PPBS反射的光束, 被QWP调制后由PBS2分离为P偏振光和S偏振光, 从PBS2透射的P偏振光由CCD3接收, 反射的S偏振光由CCD4接收.

图1 分振幅型全Stokes同时偏振成像系统原理图Fig.1. Scheme of the division-of-amplitude full Stokes simultaneous polarization imaging system.
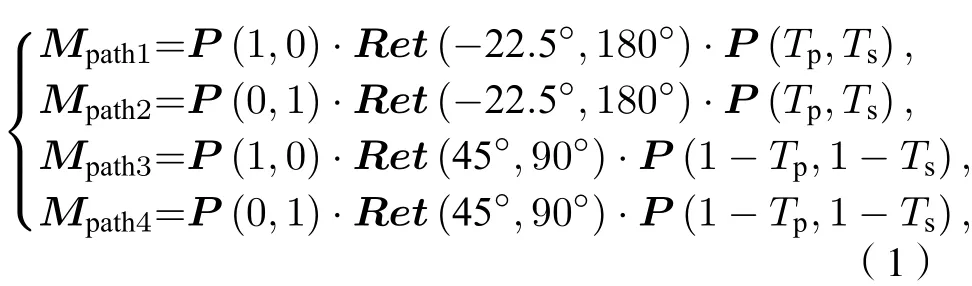
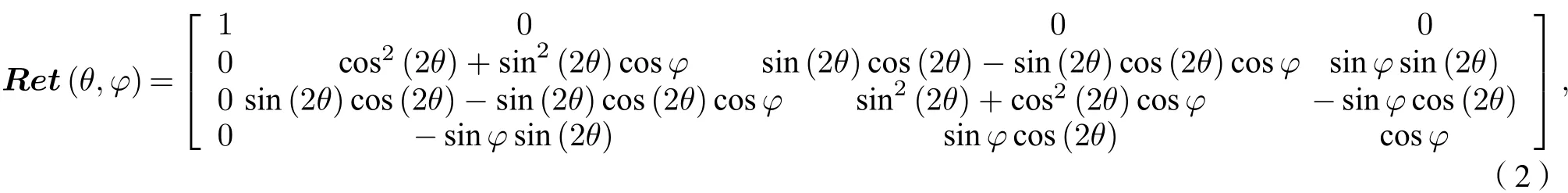
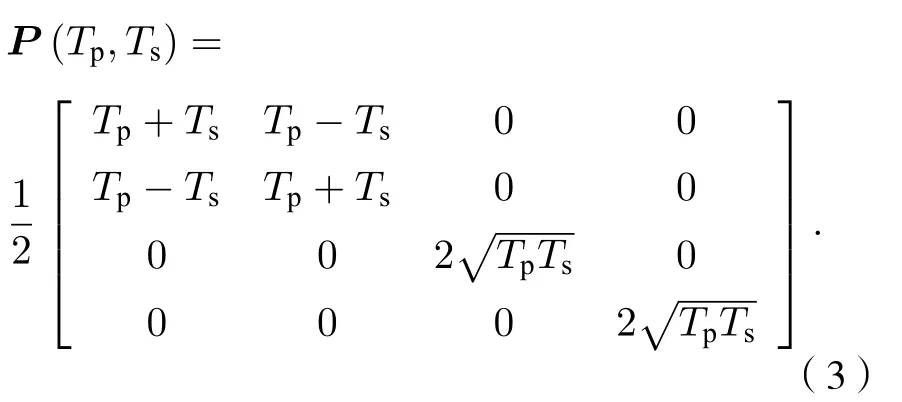
文献[20]研究了光学镜头的起偏效应. 以通常使用的玻璃进行分析, 当入射角很小(小于5°)时,角度每相差1°, 造成的偏振度测量偏差为0.01%—0.03%. 本文研究的偏振成像系统是小视场成像系统, 入射主光束的入射方向与光学镜头法线的夹角很小, 所以不考虑光学镜头的起偏效应. 分振幅型全Stokes同-时偏振成像系统4个通道的Mueller矩阵Mpath1Mpath4 为(1)—(3)式中,Tp和Ts分别为 PPBS 的 p 光透射系数和s光透射系数,P(Tp,Ts) 和P(1-Tp,1-Ts)分别为PPBS透射和反射时的Mueller矩阵;P(1,0)为PBS1和PBS2透射时的Mueller矩阵,P(0,1)为PBS1和PBS2反射时的Mueller矩阵;Ret(θ,φ)为波片(相位延迟量φ)快轴与x轴正向夹角为θ时的Mueller矩阵.
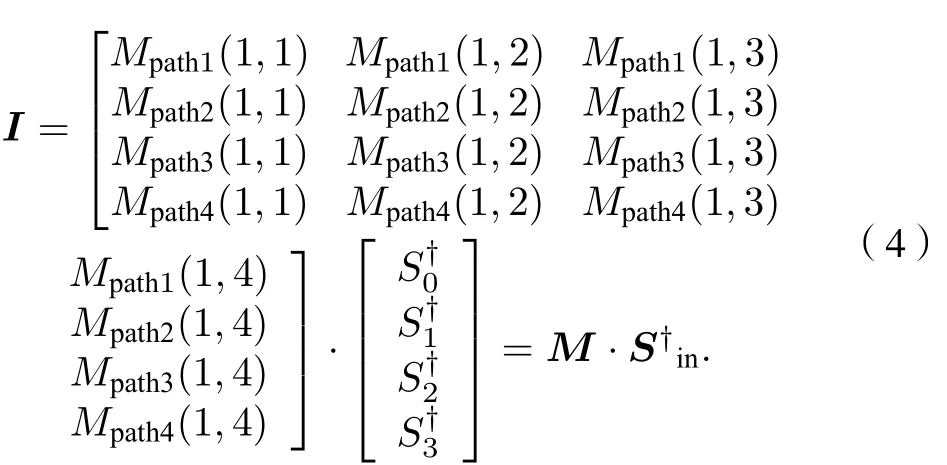
若已知测量矩阵M和光强度矢量I, 则可获得入射光Stokes矢量:
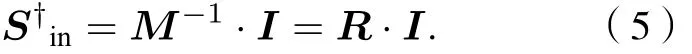
2.2 波片相位延迟误差建模
PPBS的分束比为Tp/Ts, HWP和QWP相位延迟误差分别为σ和δ时, 分振幅型全Stoke-s同时偏振成像系统4个通道的Mueller矩阵M†path1M†path4和系统测量矩阵M†分别如(6)式和(7)式所示:

实际的测量矩阵是包含HWP和QWP相位延迟误差的测量矩阵M†, 则实际的入射光Stokes矢量Sin 为
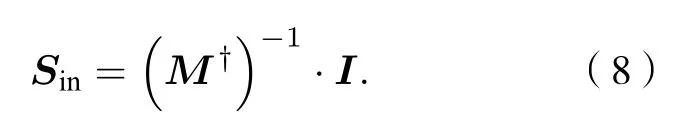
由(5)式可得计算的入射光Stokes矢量S†in,则Stokes矢量的测量误差eS为
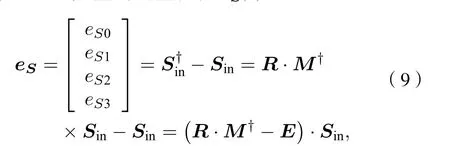
(9)式中,eSi表示Stokes矢量Si分量的测量误差(其中i= 0, 1, 2, 3),E为4 × 4单位矩阵, 矩阵R为理论测量矩阵M的逆矩阵.
对于入射光Stokes矢量, 一般关心的是光强的相对值[21], 因此, 本文在接下来的波片相位延迟误差分析中, 将入射光Stokes矢量进行归一化处理.
3 波片相位延迟误差仿真与分析
本文将采用基于典型基态入射光和基于邦加球采样的两种方法对系统中波片相位延迟误差进行仿真和分析. 基于典型基态入射光的方法通过研究典型基态入射光的Stokes矢量测量误差的变化规律便可分析出任意偏振态的入射光Stokes矢量测量误差的变化规律. 邦加球采样的方法可用于更加全面、完备地评估波片相位延迟误差对系统偏振测量精度的影响.
3.1 基于典型基态入射光的波片相位延迟误差仿真及分析
任意偏振态的入射光Stokes矢量都可分解成7 种典型基态入射光 (自然光、0°/90°/45°/135°线偏振光、右旋和左旋圆偏振光) Stokes矢量的线性组合. 通过分析7种典型基态入射光的Stokes矢量测量误差, 便可解析任意偏振态的入射光Stokes矢量测量误差.
归一化的任意偏振态的Stokes矢量Sin分解成自然光、0°/90°/45°/135°线偏振光、右旋和左旋圆偏振光Stokes矢量的线性组合表示为(10) 式中,
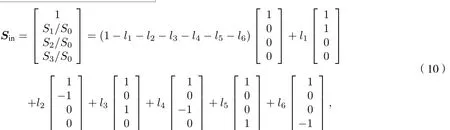
由(9)式可分别求出自然光、0°/90°/45°/135°线偏振光、右旋和左旋圆偏振光Stokes矢量的测量误差
结合(10)式可得任意偏振态的入射光Stokes矢量测量误差eS:
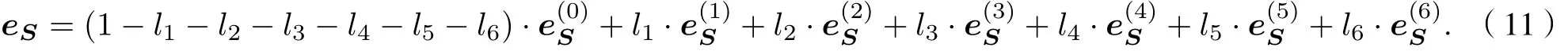
表1为分振幅型全Stokes同时偏振成像系统的设计参数, 以其为仿真参数, 则入射光分别为自然光、0°/90°/45°/135°线偏振光、右旋和左旋圆偏振光时, HWP和QWP相位延迟误差对入射光Stokes参数测量误差的影响如图2所示. 其中x轴和y轴分别为HWP相位延迟误差σ和QWP相位延迟误差δ(单位: (°)),z轴为入射光Stokes参数测量误差.
由图2可知, 系统中同时存在HWP相位延迟误差σ和QWP相位延迟误差δ时, 7种典型基态入射光S0分量和S1分量的测量误差均为0,S2分量的测量误差仅受σ的影响,S3分量的测量误差仅受δ的影响.

表1 分振幅型全Stokes同时偏振成像系统设计参数Table 1. Parameters of division-of-amplitude full Stokes simultaneous polarization imaging system.
已知7种基态入射光Stokes矢量测量误差时,利用(11)式便可解析出任意偏振态的入射光Stokes矢量测量误差. 由图2和(11)式分析可知,系统中同时存在HWP相位延迟误差σ和QWP相位延迟误差δ时, 任意偏振态的入射光的S0分量和S1分量的测量误差均为0, 任意偏振态的入射光S2分量的测量误差仅受σ的影响, 任意偏振态的入射光S3分量的测量误差仅受δ影响.
3.2 基于邦加球采样的波片相位延迟误差仿真与分析
由(9)式可知, Stokes矢量测量误差随着入射光Stokes矢量的变化而变化, 为了更加完备地评估波片相位延迟误差对分振幅型全Stokes同时偏振成像系统的Stokes矢量测量精度的影响, 需要分析不同偏振态的Stokes矢量作为入射光时波片相位延迟误差对系统的Stokes矢量测量精度的影响.
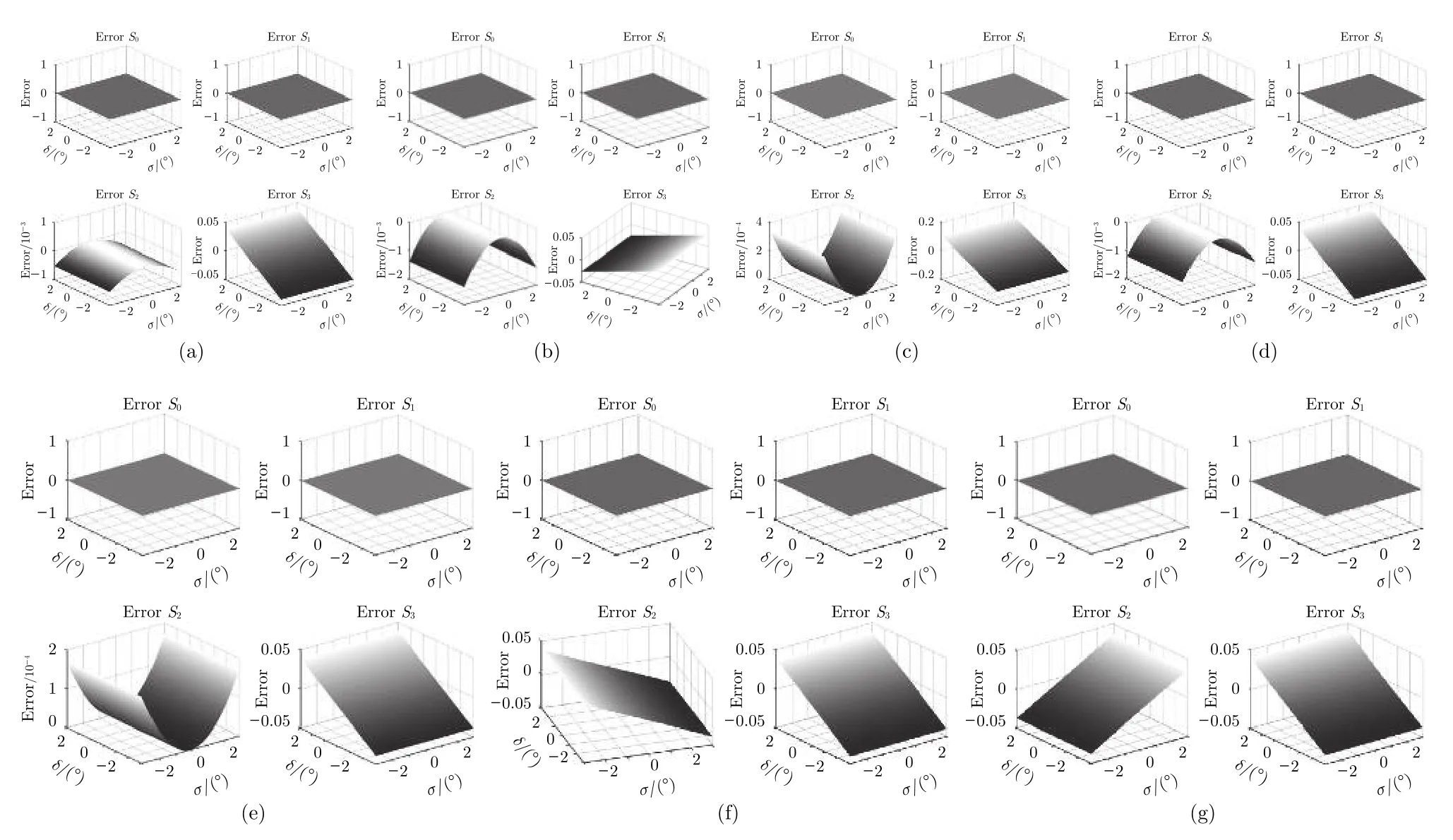
图2 不同入射光情况下的 Stokes参数测量误差 (a) 自然光; (b) 0° 线偏光; (c) 90° 线偏光; (d) 45° 线偏光; (e) 135° 线偏光;(f) 右旋圆偏光; (g) 左旋圆偏光Fig.2. Errors of Stokes parameters of different incident light: (a) Unpolarized light; (b) 0° liner polarized light; (c) 90° liner polarized light; (d) 45° liner polarized light; (e) 135° liner polarized light; (f) right circularly polarized light; (g) left circularly polarized light.
本文采用在邦加球的球面上或球内均匀地选取不同偏振态的Stokes矢量作为入射光, 进而评估HWP和QWP相位延迟误差对系统的偏振测量精度的影响. 在邦加球球面上或球内均匀采样时的任意偏振态的Stokes矢量为
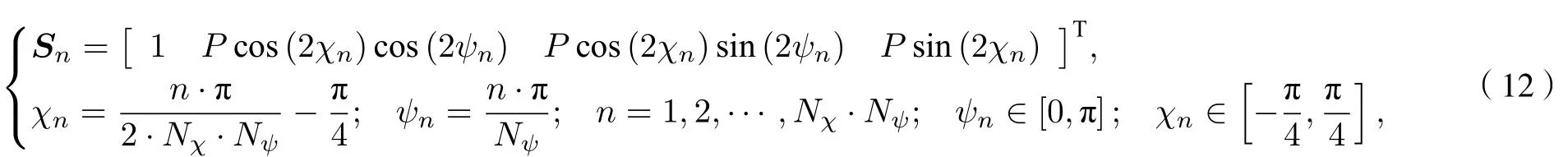
式中Sn为邦加球球面上或球内的第n个入射光采样点的归一化Stokes矢量,P为偏振度,χn和ψn分别为第n个入射光采样点Sn的椭圆度角和偏振角,Nχ表示从邦加球的南极到北极围绕球体采样的圆周个数,Nψ表示每个采样圆周上的采样点数.
令(12)式中的P= 1,Nχ= 20,Nψ= 50,则图3为邦加球球面上1000个不同偏振态的Stokes矢量的三维分布和Stokes参数的数值分布.
以表1中的系统设计参数作为仿真参数, 以图3中的1000个Stokes矢量作为入射光采样点,则图4(a)和图4(b)分别为仅存在1°的HWP相位延迟误差时和仅存在1°的QWP相位延-迟误差时1000个入射光采样点的Stokes参数S0S3测量误差. 图4中横坐标为入射光采样点从邦加球南极到北极的采样序数, 纵坐标为Stokes参数测量误差.
由图4(a)可知, HWP相位延迟误差σ仅影响入射光S2分量的测量精度, 从邦加球的南极到赤道的采样过程中(即采样序数n从1到500的过程中),S2分量测量误差的绝对值逐渐变小; 从邦加球的赤道到北极的采样过程中(即采样序数n从500到1000的过程中),S2分量测量误差的绝对值逐渐变大. 由此可知, 入射光的椭圆度角的绝对值越小, 则S2分量测量误差的绝对值越小.
由图4(b)可知, QWP相位延迟误差δ仅影响入射光S3分量的测量精度, 从邦加球的南极到赤道的采样过程中(即采样序数n从1到500的过程中),S3分量测量误差的振幅逐渐变大; 从邦加球的赤道到北极的采样过程中(即采样序数n从500到1000的过程中),S3分量测量误差的振幅逐渐变小. 由此可知, 入射光的椭圆度角的绝对值越小,S3分量测量误差的振幅越大; 入射光的椭圆度角恒定时,S3分量的测量误差随入射光的偏振角变化而变化(在邦加球赤道处, 即入射光为线偏振光时,S3分量的测量误差受入射光偏振角的影响最大).
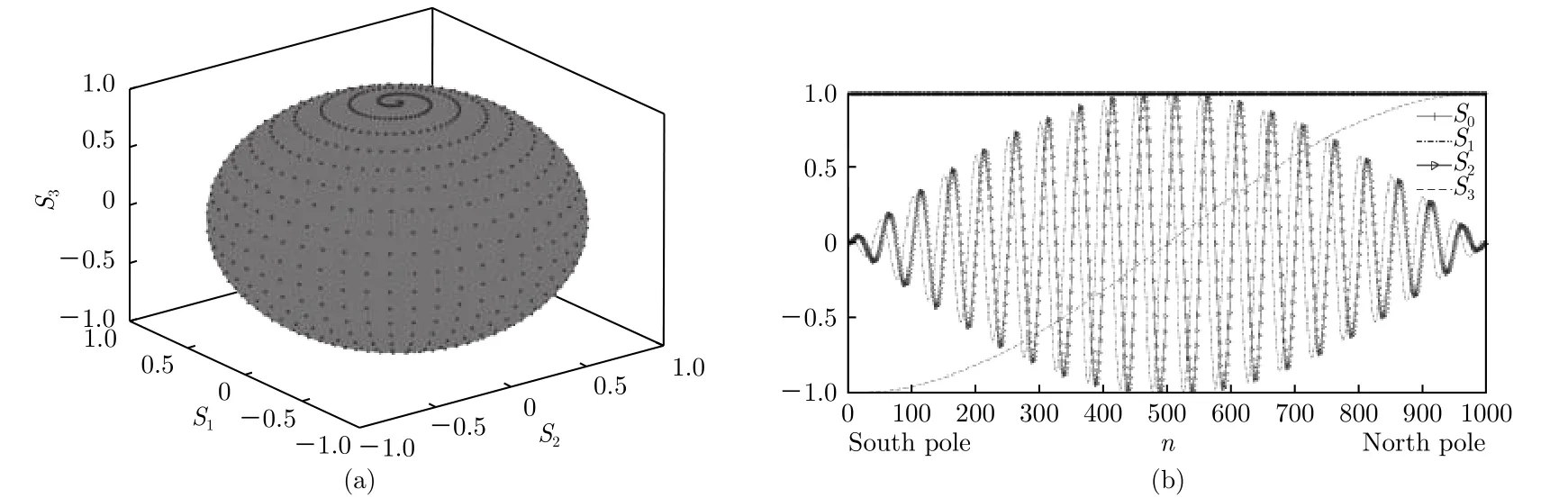
图3 邦加球球面上选取1000个不同偏振态的Stokes矢量的 (a) 三维分布和(b) Stokes参数的数值分布Fig.3. (a) 3D distribution and (b) stokes parameters values of 1000 Stokes vectors different degrees of polarization selected on the Poincaré sphere.
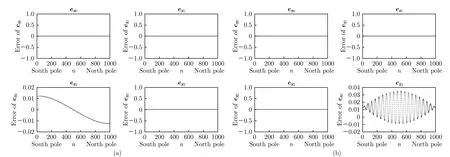
图4 1000个邦加球球面上的入射光采样点的Stokes参数测量误差 (a) 仅存在1°的 HWP相位延迟误差; (b) 仅存在1°的QWP相位延迟误差Fig.4. The measurement errors of Stokes parameters of 1000 incident light sampling points selected on the Poincaré sphere is simulated: (a) There is only 1° phase delay error of HWP; (b) there is only 1° phase delay error of QWP in the system.
HWP和QWP相位延迟误差分别为σ和δ时,入射光采样点(采样总数为Nχ·Nψ)的偏振度均为P时, 在Nχ ·Nψ个入射光采样点中Si分量测量误差绝对值的最大值(其中i= 0,1, 2, 3)为
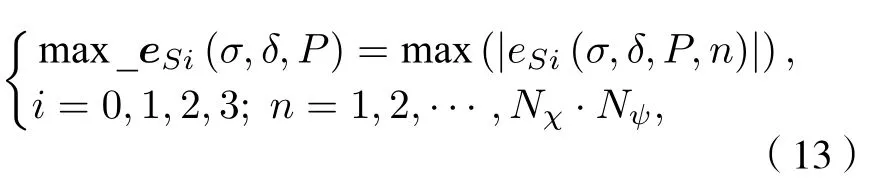

由图4可知, 仅存在1° 的HWP相位延迟误差且入射光采样点均为完全偏振光时, 偏振测量精度 a cc_S(σ=1°,δ=0,P=1) 为 1.23%; 仅存在 1°的QWP相位延迟误差且入射光采样点均为完全偏振光时, 偏振测量精度
以表1中的系统设计参数作为仿真参数, 分别令(12)式中的偏振度P为1.0, 0.8, 0.5, 0.2和0.1,不同偏振度对应的采样总数均为1000 (即(12)式中恒有Nχ= 20,Nψ= 50), 则当入射光采样点分别为邦加球球面上的完全偏振光(P= 1)和邦加球球内的部分偏振光(P为0.8, 0.5, 0.2和0.1)时,HWP相位延迟误差σ或QWP相位延迟误差δ对偏振测量精度 a cc_S(σ,δ,P) 影响的仿真结果如图5所示.
在图5(a)中, 横坐标为HWP相位延迟误差σ(单位为 (°)), 纵坐标为偏振测量精度acc_S(σ,δ=0,P), 当偏振度P恒定时, a cc_S(σ,δ=0,P) 的值随|σ|增大而增大; 当σ恒定时,acc_S(σ,δ=0,P)的值随偏振度P增大而增大.
在图5(b)中, 横坐标为QWP相位延迟误差δ(单位为 (°)), 纵坐标为偏振测量精度acc_S(σ=0,δ,P), 当偏振度P恒定时, a cc_S(σ=0,δ,P) 的值 随|δ|增 大 而 增 大; 当δ恒 定 时,acc_S(σ=0,δ,P)的值随偏振度P增大而增大.
图5(c)为HWP和QWP相位延迟耦合误差对偏振测量精度 a cc_S(σ,δ,P) 的影响,σ和δ恒定 时, a cc_S(σ,δ,P) 的 值 随 偏 振 度P增 大 而增大.
由图5可知, HWP相位延迟误差σ或QWP相位延迟误差δ恒定时, 入射光采样点的偏振度P= 1时对应的偏振测量精度acc_S(σ,δ,P=1)为最大值, 因此, 采用 a cc_S(σ,δ,P=1) 来评估分振幅型全Stokes同时偏振成像系统的偏振测量精度. 系统中同时存在HWP和QWP相位延迟误差时, 系统的偏振测量精度 a cc_S(σ,δ)定义为
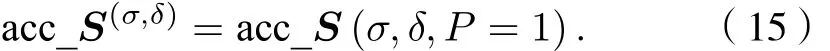
3.3 波片相位延迟误差对偏振度测量精度的影响
偏振度的测量精度是评价分振幅型全Stokes同时偏振成像系统性能的重要指标, 入射光的Stokes矢 量时 , 偏 振 度P=系统中同时存在HWP相位延迟误差σ和QWP相位延迟误差δ时, 入射光的偏振度为P时的偏振度测量误差 ΔP(σ,δ,P)为
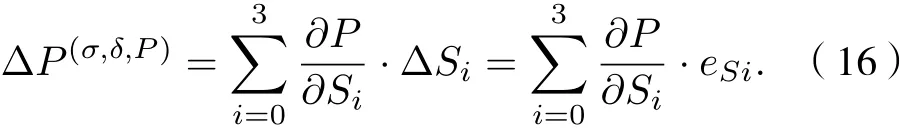
由图2和(11)式分析可知, 系统中同时存在HWP和QWP相位延迟误差时, 任意偏振态的入射光S0分量的测量误差eS0和S1分量的测量误差eS1均为0. 因此(16)式简化为

以表1中的系统设计参数作为仿真参数, 以图3中的1000个邦加球球面上(偏振度P均为1)的Stokes矢量作为入射光采样点, 则图6(a)和图6(b)分别为仅存在1° 的HWP相位延迟误差时和仅存在1° 的QWP相位延迟误差时1000个邦加球球面上的入射光采样点的偏振度测量误差.
由图6(a)可知, 系统中仅存在HWP相位延迟误差σ时, 入射光从邦加球的南极到赤道的采样过程中(或者入射光从邦加球的赤道到北极的采样过程中), 偏振度测量误差的振幅先增大后减小, 由此可知, 入射光为椭圆偏振光时,随入射光偏振角的变化而变化(入射光的椭圆度角为 ±45° 时,受入射光偏振角的影响最大). 由图6(b)可知, 系统中仅存在QWP相位延迟误差δ时, 入射光从邦加球的南极到赤道的采样过程中(或者入射光从邦加球的赤道到北极的采样过程中), 偏振度测量误差的振幅先增大后减小, 入射光为椭圆偏振光时,随入射光偏振角的变化而变化.
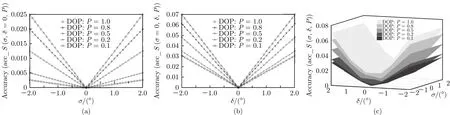
图5 不同偏振度的采样点作为入射光时对偏振测量精度的影响 (a) 仅HWP相位延迟误差; (b) 仅QWP相位延迟误差;(c) HWP和QWP相位延迟耦合误差Fig.5. When the sampling points with different degrees of polarization are used as incident light, the effect of measurement accuracy: (a) The phase delay error of the HWP; (b) the phase delay error of the QWP; (c) the phase delay errors of the HWP and the QWP on polarization.
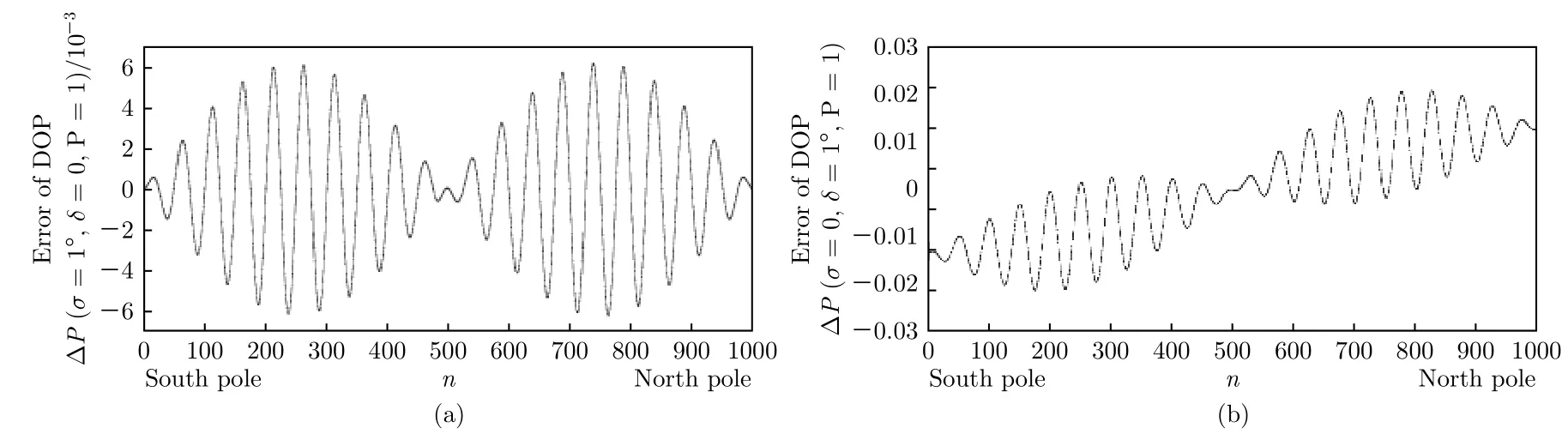
图6 1000个邦加球球面上的入射光采样点的偏振度测量误差 (a) 仅存在1°的HWP相位延迟误差; (b) 仅存在1°的QWP相位延迟误差Fig.6. The measurement errors of DOP of 1000 incident light sampling points selected on the Poincaré sphere is simulated:(a) There is only 1° phase delay error of HWP; (b) there is only 1° phase delay error of QWP in the system.
系统中存在HWP相位延迟误差σ和QWP相位延迟误差δ时, 令(12)式中的Nχ= 20,Nψ=50, 对于偏振度均为P的1000个入射光采样点,选择偏振度测量误差绝对值的最大值作为入射光偏振度为P时的偏振度测量精度 a cc_P(σ,δ,P) .由图6可知, 系统中仅存在1°的HWP相位延迟误差时, 入射光偏振度为1时的偏振度测量精度为0.61%; 系统中仅存在1°的QWP相位延迟误差时, 入射光偏振度为1时的偏振度测量精度为2.08%.
以表1中的系统设计参数作为仿真参数, 分别令(12)式中偏振度P为1, 0.8, 0.5, 0.2和0.1, 不同偏振度对应的入射光采样总数均为1000 (即(12)式中恒有Nχ= 20,Nψ= 50), HWP相位延迟误差且 QWP相位延迟误差时, 则入射光的偏振度P分别为1,0.8, 0.5, 0.2和0.1时的偏振度测量精度acc_P(σ,δ,P)的仿真结果如图7所示. 由图7可知,σ和δ恒定时, 入射光的偏振度P越大, 偏振度测量精度 a cc_P(σ,δ,P) 的值越大, 因此选择入射光的偏振度P= 1时对应的偏振度测量精度acc_P(σ,δ,P=1)来评估系统的偏振度测量精度.
以表1中的系统设计参数作为仿真参数, 以图3中1000个偏振度P均为1的Stokes矢量作为入射光采样点, 则表2和表3分别为系统的偏振度测量精度和系统偏振测量精度随HWP相位延迟误差σ和QWP相位延迟误差δ的变化关系.
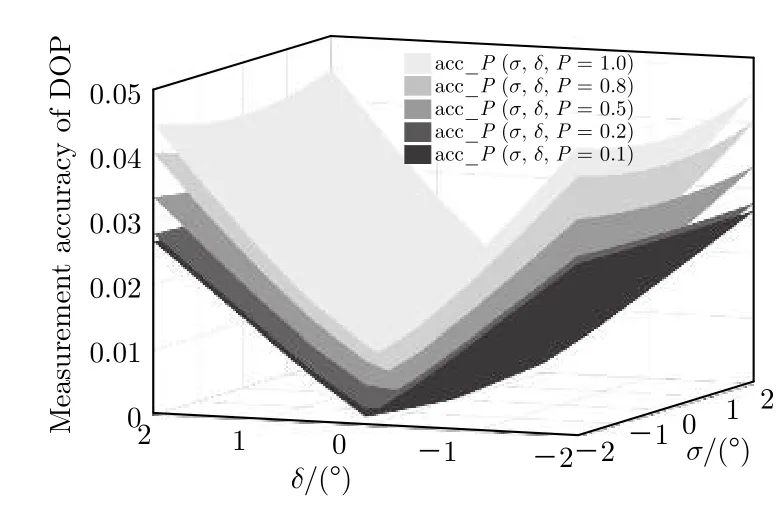
图7 入射光的偏振度 P分别为 1.0, 0.8, 0.5, 0.2和0.1时, 偏振度测量精度 a cc_P(σ,δ,P) 随HWP相位延迟误差 σ和QWP相位延迟误差 δ的变化关系Fig.7. Variation relation of measure accuracy acc_P(σ,δ,P)of DOP with the phase delay error of HWP and the phase delay error of QWP under the condition of P= 1.0, 0.8, 0.5, 0.2 and 0.1.
为了满足气溶胶光学参数探测、目标和背景偏振探测等应用需求, 要求分振幅型同时偏振成像系统的偏振测量精度优于2%. 由表2和表3可知, 系统中同时存在HWP相位延迟误差σ和QWP相位延迟误差δ时, 恒有P(σ,δ,P=1). 为保证系统偏振测量精度和系统的偏振度测量精度 a cc_P(σ,δ,P=1) 均在2%以内, 则HWP相位延迟误差应在 ±1.6°内,QWP相位延迟误差应在 ±0.5°内.
4 实验结果与分析
为了验证本文对分振幅型全Stokes偏振成像系统波片相位延迟误差分析结论的正确性, 搭建了如图8所示的实验光路, 实验光路由偏振态发生器 (polarization state generator, PSG)、四分束偏振分析器(four-paths polarization analyzer)和陷阱探测器(trap detector)组成. 其中, PSG由He-Ne激光器、激光功率控制器(laser power controller,LPC)、退偏器、安装在电动转台上的偏振片和QWP组成; 四分束偏振分析器由PPBS, HWP, QWP, PBS1和PBS2组成.

表2 系统偏振度测量精度 a cc_P(σ,δ,P=1) 随HWP相位延迟误差 σ和QWP相位延迟误差 δ的变化关系Table 2. Variation relation of measure accuracy a cc_P(σ,δ,P=1) of DOP with the phase delay error σof HWP and the phase delay error δof QWP.
光路中PSG和四分束偏振分析器的主要参数分别如表4和表5所列. 实验中四分束偏振分析器4个通道的 Mueller矩阵Mτ,path1 —Mτ,path4 为
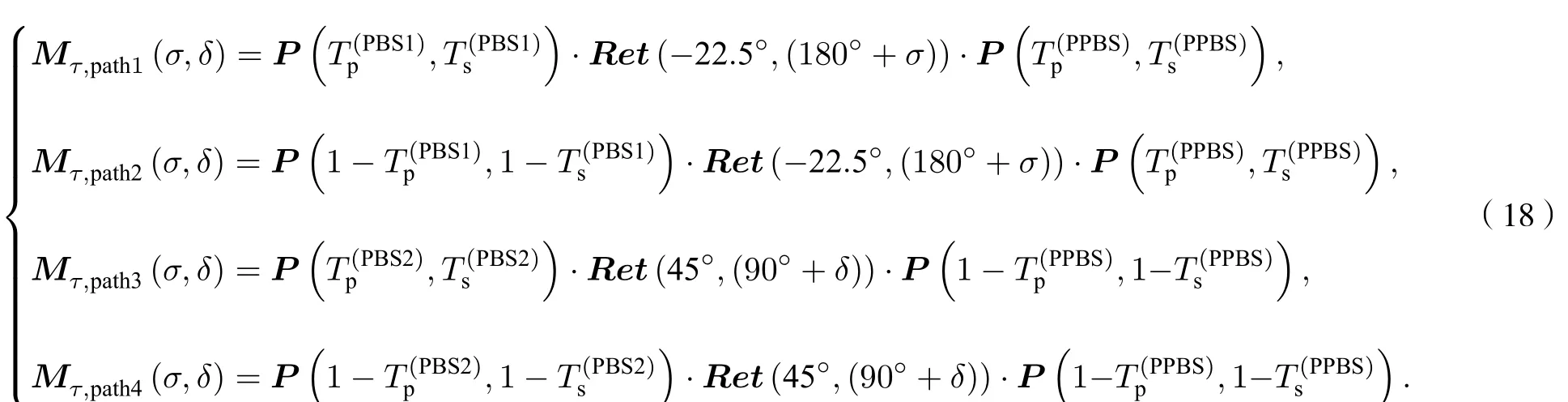

图8 波片相位延迟误差分析实验光路Fig.8. Experimental optical path of wave plate phase delay error analysis.

表4 实验光路中PSG的主要参数Table 4. Parameters of PSG in the experimental optical path.
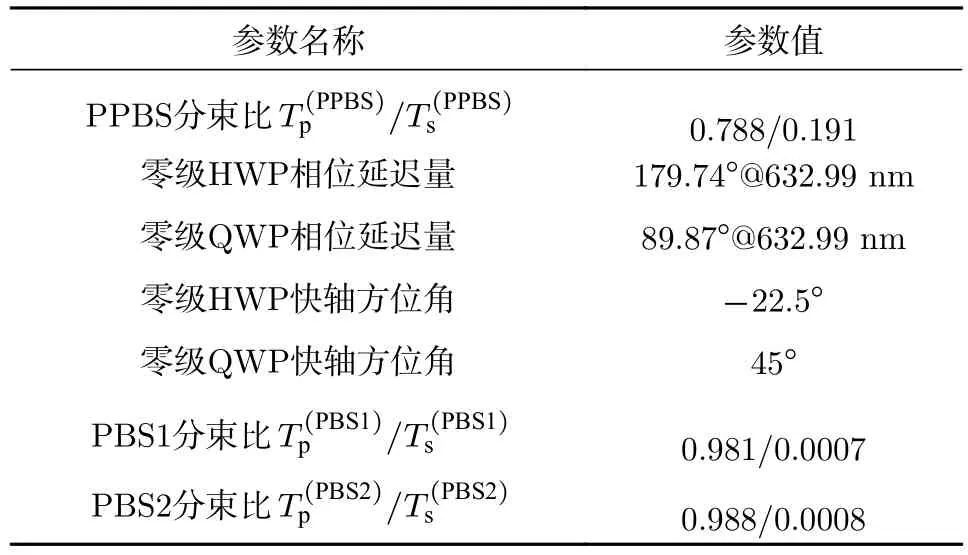
表5 实验光路中四分束偏振分析器的主要参数Table 5. Parameters of the four-paths polarization analyzer in the experimental optical path.
将表5中PPBS, PBS1和PBS2的分束比代入 (18)式, 并令σ= -0.26°和δ= -0.13°, 得到四分束偏振分析器的实际测量矩阵M1†. 将表5中PPBS, PBS1和PBS2的分束比代入(18)式,并令σ= 0和δ= 0, 得到估算的测量矩阵M0.
实验中定义入射光的传播方向为z轴的正方向, 垂直于实验平台向上为y轴的正方向(坐标系满足右手法则). 利用PSG产生偏振度为1的标准偏振光, PSG起始状态为: QWP快轴与x轴的夹角为0°, 偏振片的透光轴与x轴的夹角为-45°.将PSG中的QWP以步长ω= 6°进行逆时针旋转, PSG中的偏振片以步长ϖ=ω+0.3°=6.3°进行逆时针旋转, 同时旋转n次共产生300个不同偏振态的完全偏振光SPinSG(n) (n= 1, 2, ··, 300), 相当于(12)式中的P= 1,Nχ= 10,Nψ= 30, 均匀分布在邦加球球面上的300个采样点.
300), 入射光Stokes矢量的测量误差为e(1)(n)=
S偏振度由和可分别获得入射光的真实偏振度P(1,real)(n)和估算偏振度P(1,estimated)(n) , 偏振度的测量误差为P(1,error)(n)=P(1,estimated)(n)-P(1,real)(n)(n= 1, 2, ··, 300).
处理数据得, 光路中HWP相位延迟误差σ=-0.26°和QWP相位延迟误差δ= -0.13°同时存在时, 入射光Stokes矢量和偏振度的测量结果如图9所示, 入射光从邦加球的南极到北极的采样过程中,S0分量的测量误差和S1分量的测量误差为0 ,S2分量测量误差的绝对值先减小后增大,S3分量测量误差的振幅先增大后减小, 与图4仿真结果的变化规律一致. 入射光从邦加球的南极到赤道的采样过程中(或从邦加球的赤道到北极的采样过程中), 偏振度测量误差的振幅先增大后减小, 与图6仿真结果的变化规律相符.
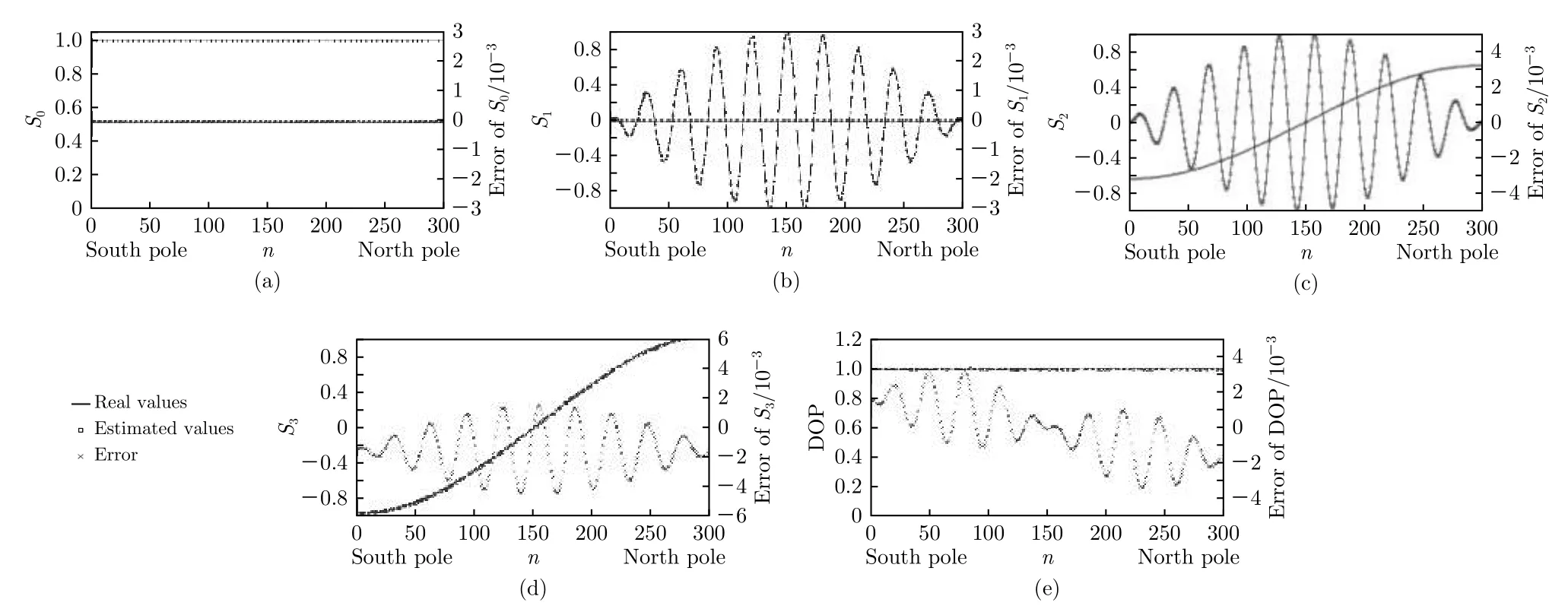
图9 实验中HWP相位延迟误差 σ= -0.26°和QWP相位延迟误差 δ= -0.13°时的测量结果 入射光 (a) S0 分量; (b) S1 分量; (c) S2 分量; (d) S3 分量; (e) 偏振度Fig.9. Measurement results: (a) S0 component; (b) S1 component; (c) S2 component; (d) S3 component; (e) DOP of the incident light under the condition of σ= -0.26° and δ= -0.13°.
图9结果显示, 偏振测量精度acc_S(σ=为0.44%, 偏振度测量精度 a cc_P(σ=-0.26°,δ=-0.13°,P=1) 为0.33%,与表2和表3的仿真结果相符合, 即HWP相位延迟误差在 ±1.6°内, 且 QWP相位延迟误差在±0.5°内时, 偏振测量精度和偏振度测量精度均小于2%.
5 结 论
本文针对分振幅型全Stokes同时偏振成像仪中HWP和QWP相位延迟误差对入射光Stokes矢量测量精度影响较大的问题, 建立了包含HWP和QWP相位延迟误差的Stokes矢量测量误差模型, 仿真了自然光、0°/90°/45°/135°线偏振光、右旋和左旋圆偏振光分别作为入射光时, HWP和QWP相位延迟耦合误差对Stokes矢量测量误差的影响, 给出了求解任意偏振态入射光的Stokes矢量测量误差的方法. 仿真结果表明, 同时存在HWP和QWP相位延迟误差时, 任意偏振态的入射光的S0分量和S1分量的测量误差均为0, 任意偏振态的入射光S2分量的测量误差仅受HWP相位延迟误差的影响, 任意偏振态入射光S3分量的测量误差仅受QWP相位延迟误差的影响. 为了更加完备地分析HWP和QWP相位延迟误差对系统偏振测量精度的影响, 本文提出分别在邦加球的球面和球内选取不同偏振度的Stokes矢量作为入射光, 在此基础上仿真了HWP和QWP相位延迟误差对偏振测量精度 a cc_S(σ,δ,P) 和偏振度测量精度 a cc_P(σ,δ,P) 的影响. 仿真结果表明, HWP和QWP相位延迟误差恒定时, 偏振测量精度acc_S(σ,δ,P)的值和偏振度测量精度acc_P(σ,δ,P)的值都随着偏振度P的增大而增大, 因此, 选取入射光偏振度为1时对应的偏振测量精度acc_S(σ,δ,P=1)和偏振度测量精度acc_P(σ,δ,P=1)来评估系统. 为保证系统偏振测量精度和偏振度测量精度均在2%内, HWP相位延迟误差应在 ±1.6°内, QWP相位延迟误差应在 ±0.5°内. 这对分振幅型全Stokes同时偏振成像系统的光学参数设计、波片相位延迟的加工精度要求和系统研制具有重要的意义.

