一种基于二阶锥规划的MTD滤波器组设计算法

贾可新，张茹斌

(华东电子工程研究所 孔径阵列与空间探测安徽重点实验室，合肥 230088)

0 引 言

在雷达监视环境中，雷达接收到的外界信号既包括运动目标的回波信号，也包括由地面物体、云雨、海浪、人为释放箔条等物体散射生成的各种杂波信号。在实际环境中接收到各种杂波的功率往往比目标回波信号强得多。这些杂波信号将对运动目标的检测能力产生严重影响。因此，雷达信号处理必须根据杂波特性自适应抑制杂波，尽可能消除杂波对目标检测的影响。[1-4]

自适应杂波抑制采用的动目标检测(MTD)技术主要是根据杂波的多普勒频率变化特性，通过合理设计多普勒滤波器组来抑制各种杂波。该技术可极大提高雷达在复杂杂波环境下的运动目标检测能力。目前，MTD多普勒滤波器组实现方法主要包括FFT滤波器组和有限脉冲响应(FIR)滤波器组方法。与基于FFT的多普勒滤波器组相比，FIR型多普勒滤波器组在抑制零频附近的杂波时更加灵活，其频率响应能在零频附近灵活形成满足指定带宽的较深零陷。

为了在零频附近灵活形成满足要求的零陷，文献[5]将阵列方向图数字综合算法[6-7]应用到MTD滤波器设计中，给出了一种自适应迭代MTD滤波器设计算法。该算法需要已知杂波的协方差矩阵，且假设杂波具有高斯型功率谱。借鉴文献[6-7]的处理思想，文献[8]提出了一种基于最大信杂比准则的MTD滤波器设计算法。该方法无需已知杂波功率谱，通过迭代运算可获得满足最大信杂比要求的最佳滤波器系数，但对调节因子和初始阻带衰减值比较敏感。若初始参数选择不合理，容易导致算法不收敛。为改善文献[8]中算法的稳健性，文献[9]提出了一种改进型MTD滤波器设计算法，降低了对调节因子和初始阻带衰减值的依赖性。文献[9]采用的迭代算法以滤波器实际阻带衰减不大于期望阻带衰减作为迭代收敛条件。在调节因子和初始阻带衰减及步进选择不合适时，这一迭代条件会导致算法出现过收敛现象，即在某些副瓣的极大值等于期望衰减值、其他副瓣的极大值小于期望衰减值时停止迭代。当算法出现过收敛现象时，文献[9]给出的滤波器系数将带来额外的加权损失。

为避免算法出现过收敛现象，降低滤波器的加权损失，本文提出了一种基于二阶锥规划的MTD滤波器组设计算法。相比于文献[9]的算法，所提算法无需设置调节因子，无需迭代更新初始阻带衰减值，收敛时的滤波器所有副瓣极大值均等于或近似等于期望衰减值，降低了滤波器的加权损失。

1 自适应MTD滤波器设计算法

常规自适应MTD滤波器设计方法通常需要已知杂波的统计特性，并根据自适应滤波器的原理计算FIR滤波器的系数。设FIR滤波器的通带中心频率为ωi，则FIR滤波器的系数为

(1)

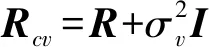
为改善常规自适应MTD滤波器设计方法的性能，文献[9]给出了一种迭代自适应MTD滤波器设计方法。该方法不需要已知杂波统计特性，而是将杂波建模为均匀分布的许多窄带杂波信号。为了能够自动控制杂波处零陷深度和副瓣电平，算法在每次迭代结束都与预先设置的滤波器期望频率响应d(ω)进行比较，若未达到要求则独立调节各窄带杂波信号的功率值，重新进行迭代。

若G(ωm,k)为第k次迭代得到的滤波器频谱，Gmax(k)为相应的通带范围内的最大值，则窄带杂波功率由第k次到第k+1次调节时的迭代公式为

(2)

(3)

(4)

其中，rm(k)=Gmax(k)/d(ωm)，Δm(k)=G(ωm,k)-rm(k)，η为调节因子。第k次调节的滤波器系数为

(5)

前述迭代MTD滤波器设计算法以滤波器实际阻带衰减不大于期望阻带衰减作为迭代收敛条件。当调节因子和初始阻带衰减及步进选择不合适时，算法也会出现过收敛现象，即在滤波器阻带范围内某些副瓣的极大值等于或近似等于期望衰减值，其他副瓣的极大值小于期望衰减值时停止迭代。当算法出现过收敛现象时，滤波器系数将带来额外的加权损失。

2 基于二阶锥规划的MTD滤波器设计算法

为避免算法出现过收敛现象，降低滤波器的加权损失，本节给出了一种基于二阶锥规划的MTD滤波器组设计算法。相比于前述MTD滤波器组设计方法，所提算法无需设置调节因子、无需迭代更新初始阻带衰减值，收敛时的滤波器阻带范围内的所有副瓣的极大值均等于或近似等于期望衰减值，降低了滤波器的加权损失。

设N阶MTD滤波器的期望阻带衰减为D(ω)dB，相应的实际值为d(ω)=10D(ω)/20，MTD滤波器的系数矢量可表示为

(6)

则满足期望阻带衰减要求的MTD滤波器系数可通过如下优化问题求得

(7)

其中，‖·‖2表示2-范数，a(ω)=[1ejω…ej(N-1)ω]T，ω0为MTD滤波器的中心频率，Ω0为MTD滤波器的阻带频率范围。

引入辅助变量t，前述优化问题可改写为

(8)

将阻带频率范围离散化为P个频点ω1,ω2,…,ωP，公式(8)可近似表示为

(9)

(10)

对于约束条件wHa(ω0)=1，可用等式约束Fx=g表示，即

(11)

(12)

对于约束条件|wHa(ωi)|≤d(ωi)，i=1,2,…,P，可用

(13)

进行重新表示，即要求

di=d(ωi),fi=0(2N+1)×1

(14)

给定滤波器的中心频率、阻带频率范围内的离散频点和期望阻带衰减值，根据前述约束条件，通过求解公式(10)的二阶锥规划问题可获得MTD滤波器系数。

3 仿真实验

本节将通过仿真实验验证所提算法的有效性。设MTD滤波器的阶数为12，滤波器总个数为13，零频附近4个滤波器的阻带衰减-35 dB，剩余9个滤波器的阻带衰减-35 dB，在零频附近归一化频率宽度0.05内零陷深度低于-60 dB。本实验仅考虑需在零频附近形成零陷的某些滤波器的设计。

采用常规自适应MTD滤波设计算法，假设杂波的功率谱密度为高斯谱，窗函数为切比雪夫窗。令归一化中心频率等于0.2283。通过人工调节窗函数的阻带电平和杂波功率，其频率响应如图1(a)所示。该滤波器的加权损失为1.2956 dB。将中心频率设置为0.45，重新调节相关参数，其频率响应如图1(b)所示。该滤波器的加权损失为1.1656 dB。由图1可知，常规自适应MTD滤波器设计算法可获得满足期望频率响应要求的滤波器，但阻带电平和杂波功率需要人工反复调节，无法自动、准确地完成相关控制参数的调节。另外，所设计的滤波器阻带范围内仅有部分副瓣的极大值等于或近似等于期望阻带衰减要求，其他副瓣的极大值小于期望阻带衰减要求。

采用文献[9]给出的迭代MTD滤波设计算法，窄带杂波个数设置为128，算法迭代次数为100。令归一化中心频率等于0.2283，调节因子η=1，设置初始阻带衰减值为-37 dB，逐次增加衰减值的步进为1 dB，经100次迭代，其频率响应如图2(a)所示。该滤波器的加权损失为1.2617 dB。保持调节因子和初始阻带衰减不变，将归一化中心频率设置为0.45，其频率响应如图2(b)所示。该滤波器的加权损失为1.1421 dB。由图2可知，文献[9]给出的迭代MTD滤波器设计算法可自动完成相关控制参数的调节，滤波器加权损失小于常规自适应MTD设计方法，但在算法收敛后阻带范围内同样仅有部分副瓣的极大值等于或近似等于期望阻带衰减要求，其他副瓣的极大值小于期望阻带衰减要求。

图1 不同中心频点处常规算法的设计结果

图2 不同中心频点处迭代算法的设计结果

采用本文提出的二次规划MTD滤波设计算法。取归一化中心频率等于0.2283，阻带范围内的离散频点个数为128。经优化计算，其频率响应如图3(a)所示。该滤波器的加权损失为1.194 dB。优化条件不变，将归一化中心频率改为0.45，其频率响应如图3(b)所示。该滤波器也满足要求，其加权损失为1.117 dB。由图3可知，所提的二次规划MTD滤波器设计算法在算法收敛后阻带范围内所有副瓣的极大值均等于或近似等于期望阻带衰减要求，滤波器的加权损失小于前述迭代算法。

4 结束语

为改善滤波器设计算法的收敛性能，本文提出了一种基于二阶锥规划的MTD滤波器设计算法。该算法通过将滤波器设计问题转换为一个基于二阶锥规划的凸优化问题，可获得满足期望阻带衰减的最优滤波器系数。相比于常规或迭代MTD算法，所提算法不需要人工设置调节因子、初始阻带衰减值等参数，在阻带范围内所有副瓣的极大值均等于期望阻带衰减要求，不会出现过收敛现象，降低了滤波器系数的加权损失。因此，本文所提算法更具有实用价值。