基于FOA-GRNN模型的转炉炼钢终点预报

，， ，

(东北大学冶金学院，沈阳110819)

随着“中国制造2025”的提出，数字化和智能化生产已成为钢铁工业抢占产业发展制高点的关键.作为当前世界上最主要的炼钢技术，转炉炼钢在传统的“高炉—转炉”生产流程中扮演着重要的角色.转炉利用氧气与铁水中各种元素的反应，来控制钢液成分与温度，其程度对钢液质量及后续生产均会产生重要影响.然而，由于众多复杂的物理化学反应带来了大量无法引入模型的影响因素，导致利用传统数学模型对该过程进行描述时，往往存在适应性差、误差较大等问题，难以满足实际生产要求[1].因此，建立更加准确、高效的转炉终点预报模型对于现场实际生产及工艺优化均具有重要的指导意义.

近年来，神经网络技术逐渐兴起，因其具有自主学习、联想储存和高速寻找最优解等优点，可学习和自适应不确定的系统并充分逼近任意复杂的非线性关系，并有效提高模型精度[2-5].本世纪初，许多学者采用常见的BP神经网络对转炉终点进行预报并取得较好的效果[6-8].但BP神经网络具有不易收敛与易陷入局部极值点等缺陷，因此RBF神经网络逐渐兴起并用于转炉终点成分的预报[9-10].尽管RBF神经网络相比BP神经网络具有易收敛的特点，但RBF的网络性能取决于神经元与扩展速度的选取，而广义回归神经网络(GRNN)作为RBF神经网络的特例，不仅具有RBF神经网络的优点，并且网络稳定性优于RBF神经网络[11-12].因此，GRNN广泛用于城市供水、建筑、通讯,轧钢、矿山与医疗[12-17]等领域，并取得了较好的效果.

本文结合国内某钢厂转炉车间实际生产数据，以非线性回归理论为基础建立了GRNN并对转炉终点温度与碳质量分数进行预报，同时采用果蝇算法(FOA)对GRNN进行优化，所得结果可为转炉实际生产与工艺改进提供重要的参考.

1 GRNN神经网络预报模型的构建

1.1 GRNN神经网络的建立

GRNN与RBF神经网络非常相似，区别就在于多了一层加和层，并去掉了隐含层与输出层的权值连接.GRNN结构分为输入层、模式层、加和层与输出层，如图1与图2所示.与其他前馈型神经网络不同的是：GRNN网络权重是由训练样本确定的，不用初始网络链接权重值、学习过程与回想过程无关、不必通过输出值与训练样本的目标值差距来修正网络链接权重值、无需迭代训练、学习过程在于寻找最佳宽度系数(亦即Spread参数值)及网络的神经元数与训练样本有关.

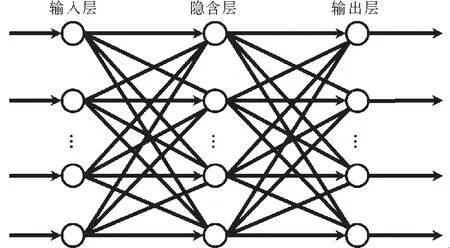
图1 RBF神经网络结构示意图Fig.1 Schematic of RBF neural network

GRNN是建立在非线性基础上，根据训练样本提供的数据逼近其隐含的映射关系，并以最大概率准则计算网络输出.设输入样本为x，输出样本为y，x、y的联合概率密度为f(x，y)，当x取x0时，y的期望为

借助Parzen非参数估计，按照下式估算概率密度函数f(x0,y)：

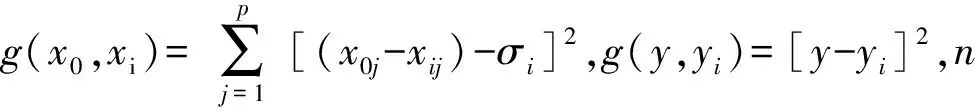
1.2 果蝇算法的引入

果蝇算法通过模拟果蝇个体的竞争与协作的行为，进而达成在空间内寻找复杂函数全局最优解的目的[18].果蝇算法具有易于理解、计算过程简单、收敛速度快及易于转化为程序代码等优点，因此受到工程领域的广泛关注.

建立GRNN网络的过程中，确定输入参量与输出参量后，网络性能仅取决于宽度系数的大小.宽度系数越大，网络对样本数据的逼近过程就越平缓，但逼近误差比较大；宽度系数越小，网络对样本的逼近性能就越好，但逼近过程就越不平缓，还有可能出现过拟合现象.由于生产过程中的测量均存在不同程度的误差，为了防止出现过拟合现象，一个合适的宽度系数十分重要.因此引入果蝇算法对GRNN网络的宽度系数进行寻优.

1.3 数据预处理

本文所采用数据基于国内某钢厂转炉车间全年生产数据，为提高神经网络模型的精度，选用Q235B的钢种冶炼数据进行神经网络的建立.在5858组实际生产数据中，筛除错误、不完整及比较离散的数据后，获得2100组有效数据，按照时间顺序选取前2000组作为训练数据，后100组作为验证数据用作模型的测试.同时，将42种参数划分为两大类(即工艺条件与原料条件).

在模型的训练过程中输入参数的过多及输入参数间相关性较低会导致预报模型的不稳定，直接影响预报模型的准确性，因此需要将输入参数进行筛选，去除非显著性因素.本文采用多元线性回归方法对输入参数与输出参数进行显著性检验，并去除显著性概率值大于0.1的输入参数[19]，最终得出表1中所示各影响因素.其中，工艺参数中对钢液温度与碳质量分数影响较大的参量有3种，包括供氧时间、冶炼周期及炉耗氧量；原料条件分为主料的成分、温度、用量与辅料的用量.

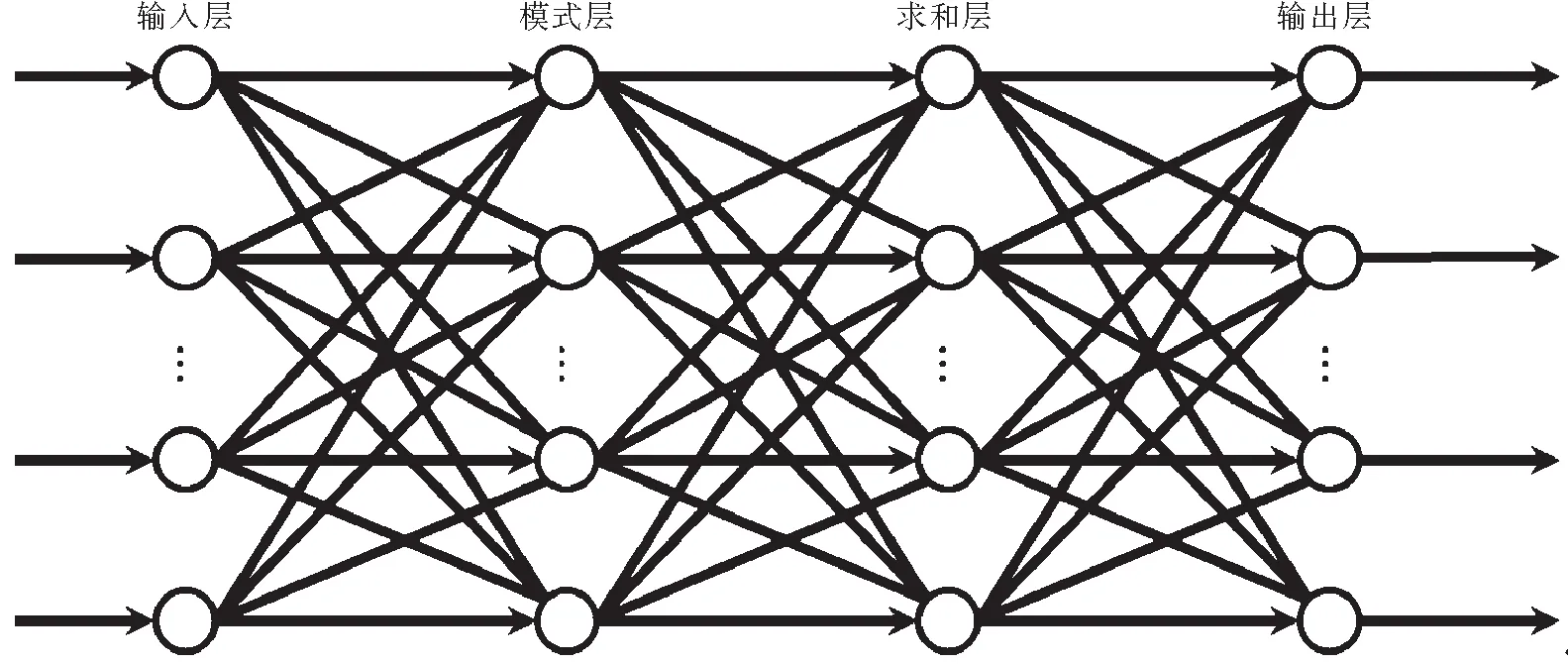
图2 GRNN神经网络结构示意图Fig.2 Schematic of GRNN neural network

数据类别输入参量输出参量工艺参数原料条件供氧时间海绵铁冶炼周期w[C]iron炉耗氧量w[Si]iron铁水温度铁水量石灰钢液中碳质量分数工艺参数供氧时间冶炼周期炉耗氧量原料条件废钢量w[C]iron轻烧白云石w[Si]iron铁皮球w[Mn]iron海绵铁w[P]iron锰矿w[S]iron硅铁铁水温度钢液温度

实际生产过程中，炉耗氧量与铁水硅含量等不仅单位不同，且相应的数值上相差可达6～7个数量级.这会导致数量级较大的数据将数量级较小的数据湮没，影响模型收敛速度与计算精度.为此需要将数据进行标准化处理，将数据处理到[0,1]区间内：计算公式如下所示：

(1)

式中：x0为标准化后的数据；x为初始数据；xmin为某组数据的最小值；xmax为某组数据的最大值.

1.4 预报模型的构建

基于前文所述，将果蝇算法用于优化GRNN的宽度系数.果蝇算法共有四个参数，包括初始值(X,Y)、迭代步长Length、种群规模Sizepop及迭代次数Maxgen.图3为果蝇算法迭代寻优流程图，列举了果蝇算法流程，具体步骤如图3所示：

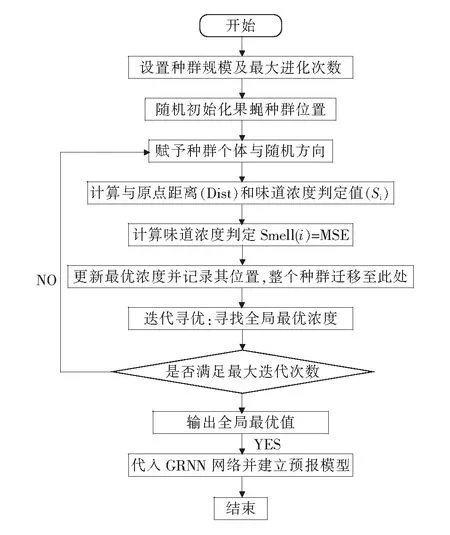
图3 果蝇算法迭代寻优流程图Fig.3 Flow chart of FOA

2 转炉终点预报结果

以FOA-GRNN模型预报转炉终点碳质量分数为例，采用果蝇算法对GRNN神经网络中参数进行优化时，果蝇群体初始位置随机初始化，果蝇群体数量为30个，迭代次数为100次，迭代搜寻方向为[-1，+1].果蝇针对宽度系数优化路线如图4所示，果蝇群体由初始点逐渐平稳飞行至(1.60091,1.02881)这一坐标使结果收敛并保持稳定.如图5果蝇算法迭代结果所示，果蝇算法迭代至第33步时，均方差收敛至0.04707并保持稳定直至迭代结束.

图4 果蝇算法迭代飞行路径 Fig.4 Flying route of fruit fly in FOA

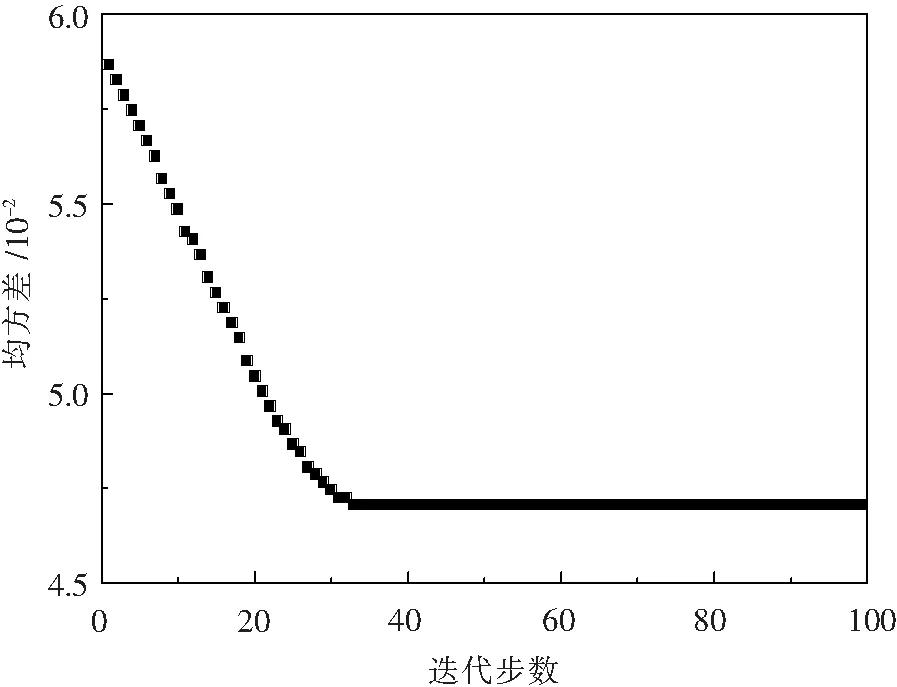
图5 迭代结果 Fig.5 Iteration Results

图6为RBF与FOA-GRNN神经网络预报模型对转炉终点温度与碳质量分数预报结果与实际结果对比图.由图中可以看出RBF与FOA-GRNN神经网络预报模型预报值与实测值相差较小，两模型温度与碳质量分数预报值的偏差分别集中在±15℃与±0.03%范围内.由此可见RBF与GRNN神经网络预报模型对转炉终点温度与碳质量分数均具有较高的预报精度.由图6(a)与(b)可见，相比于RBF，GRNN对终点温度的预报值较高，同时，在误差为±15℃内的FOA-GRNN模型的命中率高于RBF模型.由图6(c)与(d)可见，两种模型对转炉终点碳质量分数进行预报结果有较大的差异.与RBF模型相比，FOA-GRNN模型的预报值较为集中，使FOA-GRNN模型在误差为±0.03%时的命中率高于RBF模型.

图7为RBF与FOA-GRNN神经网络预报模型预报误差分布图.由图7(a)中可见，RBF模型对碳质量分数预报误差为±0.04%时，共有99组数据在此区间内，命中率达到99%；当预报误差在±0.03%范围内时模型命中率为91%.RBF神经网络预报模型的预报精度虽可满足生产要求，但仍有改进的空间.采用FOA-GRNN模型对碳质量分数预报误差在±0.04%区间内的数据为99组，命中率达到99%；误差分布在±0.03%区间内的数据为94组，命中率达到94%.由图7(b)可见，FOA-GRNN模型对转炉终点温度的预报结果优于RBF神经网络预报模型.RBF与FOA-GRNN神经网络预报模型对温度的预报误差分布在±15℃区间内的数据分别为89组与97组，命中率分别为89%与97%；预报误差分布在±20℃区间内的数据分别为95组与99组，命中率分别为95%与99%.

由此可见，与RBF模型相比，FOA-GRNN模型对转炉终点温度与碳质量分数预报的精度均具有优势.转炉终点温度与碳质量分数预报模型准确率的提升可减少补吹次数、优化工艺流程、降低能耗及生产成本、提高生产效率与钢液质量.

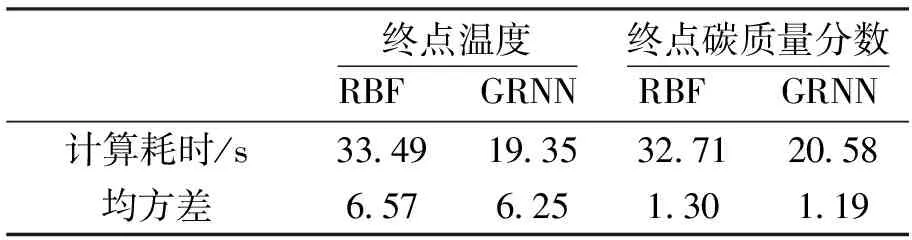
表2 两种预报模型性能对比Table 2 Comparison of performance of the two models

为更好地比较两种神经网络预报模型性能，引入计算耗时与均方差对预报模型的性能进行评价.表2为RBF网络与FOA-GRNN网络预报模型性能对比.由表中对比可以看出对终点温度与碳质量分数预报结果中，RBF模型计算耗时分别为33.49 s与32.71 s；FOA-GRNN模型计算耗时明显较低，分别为19.35 s与20.58 s.由此可见，采用FOA-GRNN模型对转炉终点温度与碳质量分数进行预报可以在RBF模型的基础上减少42.22%与及37.08%的时间，显著提高了预报效率.同时，通过对比两模型对转炉终点温度与碳质量分数的预报值与实测值的均方差可见，FOA-GRNN模型的均方差分别为6.25与1.19小于RBF模型的6.57与1.30.因此，与RBF网络模型相比，FOA-GRNN模型在对转炉终点温度与碳质量分数的预报过程中以较少的计算资源获得更准确的结果，并具有方便训练、适应性好及易于向现场推广等优点.

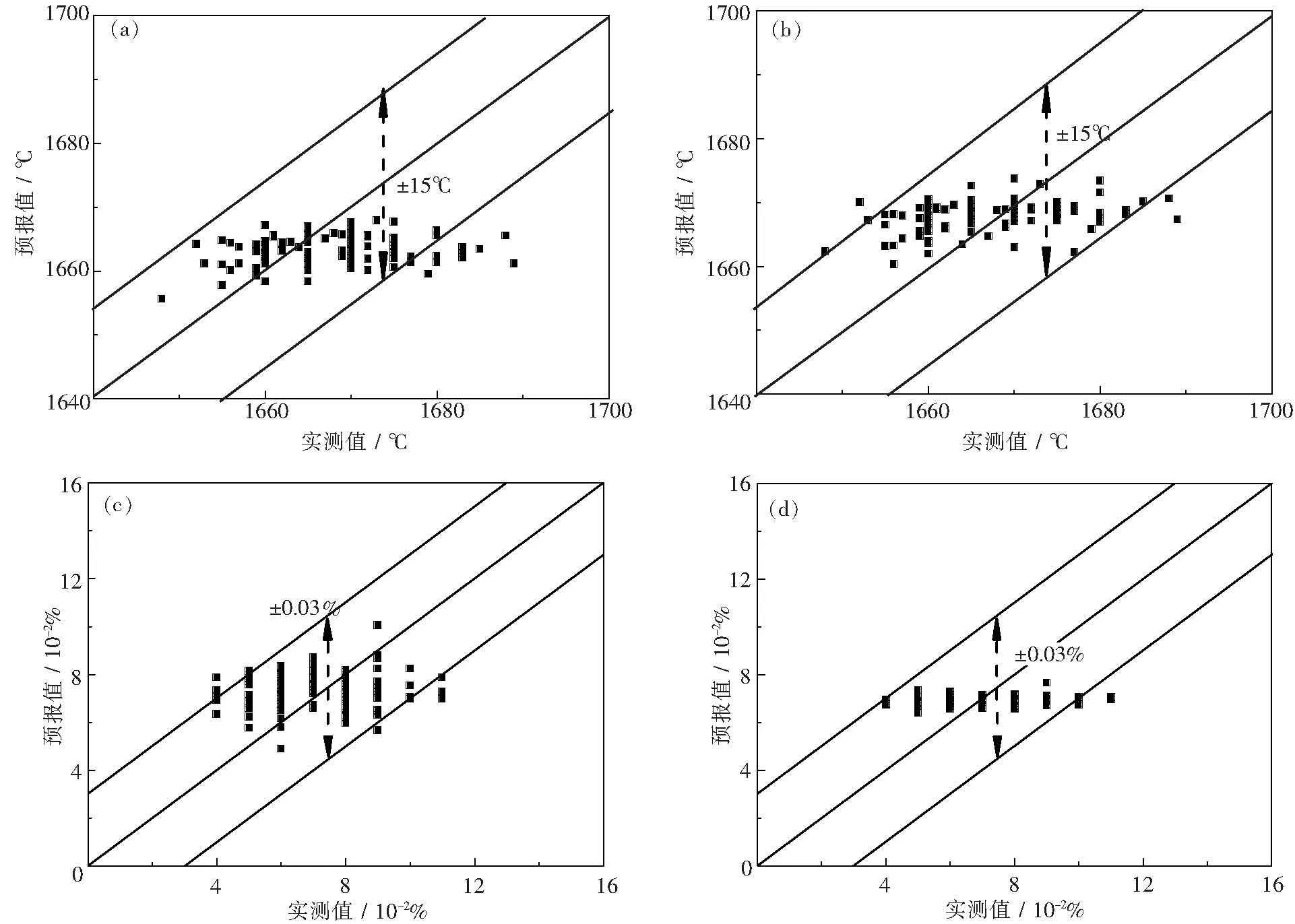
图6 终点温度与碳质量分数预报结果Fig.6 Predictions of end-point temperature and carbon content(a)—RBF模型预报终点温度；(b)—GRNN模型预报终点温度； (c)—RBF模型预报终点碳质量分数；(d)—GRNN模型预报终点碳质量分数

图7 两种预报模型结果分布对比Fig.7 Comparison of prediction results based on the two models(a)—两种模型碳质量分数预报误差分布图； (b)—两种模型温度预报误差分布图

3 结 论

本文以国内某钢厂转炉车间全年实际生产数据为基础，建立FOA-GRNN神经网络模型对转炉终点温度及碳质量分数进行预报并与RBF神经网络预报模型结果进行对比.结果表明：

(1) FOA-GRNN神经网络报模型与RBF神经网络预报模型对转炉终点温度与碳质量分数预报结果均分别集中于误差为±15℃与±0.03%的范围内.与RBF模型预报结果相比，FOA-GRNN模型预报结果在此误差范围内分布更好.

(2)采用FOA-GRNN模型对碳质量分数预报误差为±0.03%时的命中率可以达到94%，高于RBF模型的91%；FOA-GRNN模型对终点温度预报误差为±15℃时的命中率可以达到97%，高于RBF模型的89%.与RBF神经网络预报模型相比，FOA-GRNN模型具有较高的精度.

(3) FOA-GRNN神经网络预报模型与RBF神经网络预报模型相比，可降低42.22%与37.08%的计算时间并减小预测值与实测值的均方差，因此FOA-GRNN神经网络具有计算耗时少、精度高、方便训练及易于向现场推广等优点，可为现场工艺参数的制定与新钢种的开发提供重要的参考.