地下破碎矿体数值计算模型的构建及采场结构参数优化

刘冬，邵安林，金长宇，丁成功，范富泉



地下破碎矿体数值计算模型的构建及采场结构参数优化

刘冬1，邵安林2，金长宇2，丁成功2，范富泉2

(1. 汕头大学工学院，广东 汕头，515063； 2. 东北大学 资源与土木工程学院，辽宁 沈阳，110819)

以焦家金矿−390 m中段为试验采场，对采场进路跨度进行优化研究。通过现场观测、节理扫描、声波测试确定矿体的地质情况与力学特性，建立适合模拟破碎矿体的数值计算模型；利用Hoek-Brown强度准则与反分析手段确定计算参数，结合FLAC3D数值模拟对6种不同跨度的进路进行分析计算。研究结果表明：当采场进路跨度从3.5 m增加至6.5 m时，顶板的位移、塑性区体积随跨度增大而呈线性增加；当采场跨度大于7.5 m后，采场顶板的位移、塑性区体积随跨度增大而急剧增大，围岩进入塑性阶段；当−390 m中段进路跨度为7.5 m时，可以满足矿岩体的自稳要求，证明本文分析方法是正确而且可行的。

岩体力学；破碎矿体；进路跨度；优化分析；数值模拟

焦家矿床主矿体赋存于焦家断裂带的黄铁绢英岩化花岗质碎裂岩中，矿体为焦家破碎带，其稳固性较差。为保证生产安全，该矿床长期采用长×宽为3.5 m×3.5 m的小断面进路进行开采，生产效率较低。为了提高焦家金矿的开采效率，同时保证采场的稳定性，需对采场进路跨度进行优化设计，以保证回采工作安全高效运行。地下采场的稳定性是一个极其复杂的岩体工程问题，既决定了采场暴露面的跨度，也是采矿方法和地压控制方法选择的主要依据[1−3]。BARTON等[4]于1974年提出了岩体质量(Q)分类方法。南非科学与工业研究委员会(CSIR)于1976年提出了一种岩体质量评级体系(RMR)方法。MATHEWS等[5]以Q系统为基础，提出一种稳定性图表法即Mathews稳定性图表法。PAKALNIS等[6]在RMR基础上，总结出临界跨度图表法用于软弱岩体的采场设计。需要指出的是，Mathews稳定性图表法和临界跨度设计法在国内较少应用于采场稳定性研究，主要原因是我国尚未建立采场设计参数与岩体质量的图表关系，缺少基于矿山开采稳定性统计的数据库。近些年，随着计算机技术的发展，岩土工程中稳定性问题更多采用数值模拟方法进行研究[7−13]。本文针对焦家金矿矿岩破碎特性，通过现场节理调查与力学测试等方法，利用Hoek−Brown强度准则确定节理岩体的基本力学参数；借助损伤力学理论，建立适合模拟破碎节理岩体的本构模型；以FLAC3D为平台，对焦家金矿−390 m中段的缓倾斜、中厚、破碎矿体的进路跨度进行参数优化，并综合Mathews稳定性图表法确定进路跨度。

1 本构模型

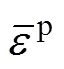
为了定义岩体变形与强度参数的变化，先假设各个参数满足如下方程：

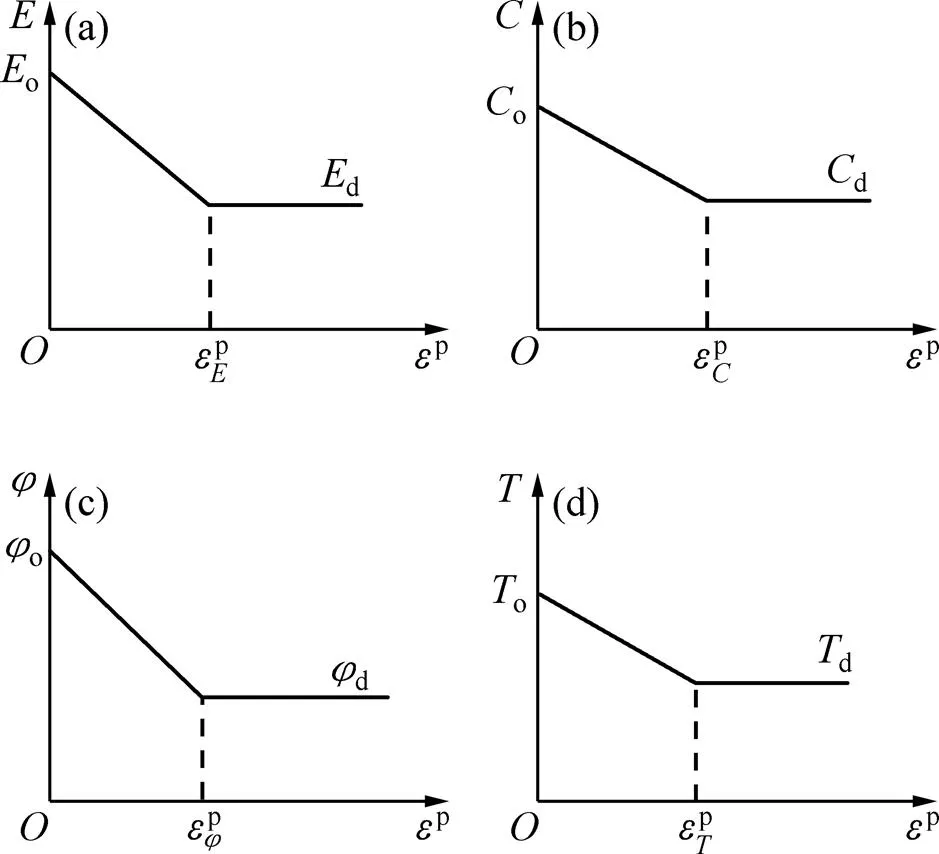
(a) 弹性模量；(b) 内聚力；(c) 摩擦角；(d) 抗拉强度

剪切屈服函数采用Mohr-Coulomb 屈服准则与最大拉应力强度准则(Rankine准则)，其表达式如下：

式中：s为剪切屈服函数；1为最大主应力；3为最小主应力；N为中间变量；t为拉伸屈服函数；t为岩石单轴抗拉强度。

最后，通过C++编程语言编制dll动态链接库 文件。

2 工程概况

焦家金矿−390中段为主要回采中段，该中段矿体总体走向为NE54°，倾向为NW，倾角为26°左右，为缓倾斜矿体，厚度为中厚。在矿体上盘裂隙交汇部位，岩石比较碎，其稳固性相对较差，极易形成三角冒落。矿体下盘围岩为绢英岩化、硅化及钾化花岗岩，其内亦发育相互交错的裂隙节理，造成局部围岩破碎。因此，该矿体长期采用跨度为3.5 m的上向水平分层进路充填采矿法进行回采，如图2所示(其中−，−和−分别为各剖面线的位置)。这种开采方法严重制约矿山生产能力，使矿山生产效率较低。因此，如何合理确定采场跨度，实现矿床安全高效开采，是焦家金矿面临的主要难题。

1—已充填进路；2—炮孔；3—待回采进路；4—通风充填井；5—分段运输巷；6—分层连巷；7—泄水井；8—崩落矿石；9—阶段运输巷；10—出矿穿脉；11—人工假底。

3 岩体力学参数

Hoek-Brown强度准则为节理岩体力学参数的选取提供了理论依据。在Hoek-Brown强度准则中，地质强度指标(GSI)是1个极其重要的岩体参数。该参数与岩体完整度、节理粗糙度、节理风化程度和填充物性质等密切相关。由于上述参数在选取时存在主观性，因此，胡盛明等[16]引入岩体体积节理数J，通过图表法对GSI进行量化，提高了GSI参数的客观性。本文作者通过调查获取焦家金矿−390 m中段岩体体积节理数J，利用该参数计算获得数值模拟所需要的基本力学参数。

3.1 岩体节理三维扫描

为了全面获取焦家金矿−390 m中段的节理信息，采用奥地利3GSM公司生产的ShapeMetrix3D进行不接触扫描。该设备通过获取岩体表面的影像信息，利用相应软件分析系统对影像信息进行处理，从而确定详细的节理地质信息。

节理三维扫描区域为焦家金矿−390 m中段第100条勘探线与106条勘探线之间采场，采用区域测绘暴露面长度方法对调查范围的暴露面进行岩体结构调查。该进路暴露面长度共计90 m，沿其长度方向将其离散为18个宽×高为5 m×3 m的小区域分别进行测绘(根据规定每个量测的面积不应小于5 m×2 m)。三维节理扫描区域中的测点分布如图3所示。

利用ShapeMetrix3D合成岩体表面节理三维模型，如图4所示。通过该方法可以掌握−390 m中段岩层中节理的分布情况。

根据矿体巷道内18个测试区域节理发育情况，可将节理分为3组，通过ShapeMetrix3D获得的节理参数计算值与实测值对比如表1所示。由表1可知：ShapeMetrix3D计算值与罗盘实测值十分接近，说明本文采用的岩体节理三维扫描方法是可靠的。

3.2 岩体体积节理数Jv

岩体体积节理数J定义为单位体积岩体中的节理条数，国际岩石力学委员会推荐用它来定量评价岩体的完整性。目前，J测量方法大体可分为3种即直接测量法、间距法、条数法。直接测量法和间距法都至少需要有2个或2个以上近于正交的临空面，才能确定岩体中节理的数量，而本次三维节理扫描只能获得巷道壁上的节理分布与数量，因此，本文采用条数法对节理进行统计。

图3 三维节理扫描区域中的测点分布

表1 ShapeMetrix3D获得的节理参数与实测值对比

图4 18号区域节理三维模型

条数法是指利用单位测量面积内的节理条数乘以修正经验系数计算得到J的方法。一般是通过测量大量样本，取其平均值来计算J[17]。

式中：n为第个单测量面内节理数；为样本个数，一般不小于10。根据矿体巷道内18个单测量面内的节理数目，可以直接获得单位面积内节理的数量。不同测试区域节理数目见表2。考虑到焦家金矿为破碎矿体，节理数较多，同时施工对岩体造成损伤与弱化，使节理数增多，因此，取修正经验系数为1.5，由此可得−390 m中段内岩体体积节理数(J)为8.9条。

3.3 节理岩体初始力学参数计算

根据现场地质勘查与岩体体积节理数可以确定Hoek-Brown强度准则所需的基本评价指标，见表3。结合表3，利用Hoek-Brown强度准则计算获得焦家金矿−390 m中段岩体开挖扰动前的初始力学参数，见表4。

由于本文采用的数值计算模型需要确定岩体损伤后的各力学参数，为此，本文借助声波检测方法确定进路松动圈范围，利用反分析手段获取各个岩体参数的残余值(见表4)，具体方法参见文献[18]。图5所示为计算获得的岩体松动圈与现场实测的围岩松动圈对比，其中A31-1~A31-4分别为4个不同位置的声波测试钻孔。由图5可知：计算获得的松动圈与实测松动圈范围比较接近，说明本研究中岩体参数取值合理。

表2 不同测试区域节理数目

表3 Hoek-Brown强度准则所需的基本评价指标

表4 岩体力学参数

图5 计算与实测松动圈对比

4 数值分析

4.1 计算方案

为了确定进路稳定跨度的极限值，参考国内外同类工程的成功案例，确定3.5，4.5，5.5，6.5，7.5与8.5 m跨度的巷道方案。利用FLAC3D对不同进路跨度的稳定性进行计算，通过比较巷道围岩位移场与塑性区，从而确定进路跨度的极限值。

4.2 计算模型

根据−330~−390 m阶段的地质资料，建立矿体三维形态模型与数值计算模型，分别如图6和图7所示。模型水平方向长400 m，高度为250 m，厚度200 m，共计206 250个节点，338 483个单元。

图6 矿体三维形态模型

图7 矿体三维计算模型

4.3 边界条件

模型计算的位移边界条件利用遗传算法优化神经网络反演得到。根据多元线性回归计算结果、实测地应力特征和工程地质分析，采用均匀设计方法，将数值计算的位移边界条件和重力修正系数共5个参数各分为5个水平。样本水平设计方案如表5所示(其中沿矿体走向为方向，垂直矿体走向为方向)。由此构造30组学习训练样本试验组合方案，并另外构造5组测试样本用于测试网络预测效果。

将均匀设计得到的边界条件的各组样本方案代入FLAC3D进行计算，获得每个样本的3个测点处的应力计算值，作为神经网络的学习训练输入值，而将设定的边界条件作为对应输出值，建立测点应力分量和边界条件非线性映射关系的进化神经网络模型。在这一过程中，采用遗传算法优化神经网络的最佳网络结构和连接权值。在计算过程中，得到的神经网络的最佳网络结构为36−45−9−5，即输入层为36个节点，中间隐含层为2层，第1层的节点数为45，第2层的节点数为9，最后输出层为5个节点。利用该训练好的进化神经网络模型，输入各个测点的实测应力分量，得到数值计算的位移边界条件和重力修正系数，见表6。

表5 样本水平设计方案

表6 反演得到的位移边界条件和重力修正系数

4.4 数值计算结果

通过对现场回采过程数值模拟计算，得到不同采场进路跨度下顶板位移与塑性区体积，如表7所示。经分析发现，采场进路的变形主要体现为采场顶板的下沉。顶板的位移为2.50~7.41 mm(见表7)。根据计算结果，得到顶板位移与塑性区体积随采场跨度的变化，如图8所示。由图8可知：当采场进路跨度从3.5 m增加至6.5 m时，顶板的位移随跨度增大而呈线性增大；当采场跨度大于7.5 m时，采场顶板的位移随跨度增大而急剧变大，说明当跨度增加到7.5 m时，围岩已进入塑性阶段状态。不同跨度下围岩塑性区分布如图9所示。由图9可知：采场进路顶板的破坏模式主要为拉张破坏，塑性区深度为0.5~1.0 m，而进路两帮部位以岩体与节理的剪切破坏为主。对不同跨度下岩体塑性区体积进行统计可以发现(见图8)：当采场跨度从3.5 m增加至6.5 m时，塑性区体积基本随采场跨度增大而呈线性增大；当采场跨度大于7.5 m时，塑性区体积随跨度增大而急剧增大，说明岩体稳定性恶化，易发生垮落失稳现象。

表7 不同采场跨度下顶板位移与塑性区体积

图8 顶板位移与塑性区体积随跨度的变化

跨度/m：(a) 3.5；(b) 4.5；(c) 5.5；(d) 6.5；(e) 7.5；(f) 8.5

综合以上对进路顶板位移与岩体塑性区计算结果的分析可知：当采场进路跨度小于6.5 m时，采场围岩处于弹性阶段状态；当采场进路跨度大于7.5 m时，进路围岩进入塑性阶段状态，存在失稳垮落风险。根据文献[19]和[20]可知进路跨度6.5~7.5 m是岩体失稳的临界跨度区间。结合文献[21]，可确定焦家−390 m中段进路跨度为7.5 m。

5 结论

1) 通过引入等效塑性应变指标，并假设岩体各参数为满足等效塑性应变的函数，构建适合模拟破碎矿体的数值计算模型。

2) 利用岩体三维节理扫描方法获得焦家金矿−390 m中段岩层中节理分布情况，通过条数法确定岩体体积节理数v为8.9条；利用Hoek-Brown强度准则与反分析手段确定了岩体力学参数的初始值与残余值。

3) 焦家金矿−390 m中段试验采场跨度为7.5 m，该跨度可以保证矿岩体的稳定性，说明本文采用的数值模拟方法是正确且合理的。

[1] FENG Xiating, HUDSON J. The ways ahead for rock engineering design methodologies[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 255−273.

[2] FENG Xiating, HUDSON J. Rock engineering design[M]. London, UK: CRC Press/Balkema, 2011: 322−341.

[3] BROWN E T. Block caving geomechanics[M]. Queensland, Australia: Julius Kruttschnitt Mineral Centre, 2003: 12−22.

[4] BARTON N, LIEN R, LUNDE J. Engineering classifications of rock masses for the design of tunnel support[J]. Rock Mechanics, 1974, 6(6): 189−236.

[5] MATHEWS K, HOEK E, WYLLIE D, et al. Prediction of stable excavations for mining at depths below 1000 metres in hard rock[R]. Ottawa, Canada: Nature Resources Canada, 1980: 18−46.

[6] PAKALNIS R, BRADY T, HUGHES P，et al. Weak rock mass design for underground mining operation[C]// Proceedings of the 53rd Annual Conference. Ottawa, Canada: Canadian Geotechnical Society, 2000: 2−24.

[7] CHENG Yunming, WANG Jin'an, XIE Guangxiang, et al. Three-dimensional analysis of coal barrier pillars in tailgate area adjacent to the fully mechanized top caving mining face[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(8): 1372−1383.

[8] JIANG Quan, FENG Xiating, XIANG Tianbing, et al. Rockburst characteristics and numerical simulation based on a new energy index: a case study of a tunnel at 2,500 m depth[J]. Bulletin of Engineering Geology and the Environment, 2010, 69(3): 381−388.

[9] 王猛, 霍昱名, 孙尚旭, 等. 似膏体充填开采沉陷的FLAC3D数值模拟[J]. 金属矿山, 2016, 45(5): 163−167. WANG Meng, HUO Yuming, SUN Shangxu, et al. Numerical simulation on the subsidence of the paste-like filling mining based on FLAC3D[J]. Metal Mine, 2016, 45(5): 163−167.

[10] 吴启红, 万世明, 彭文祥. 一种多层采空区群稳定性的综合评价法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2324−2330.WU Qihong, WAN Shiming, PENG Wenxiang．A comprehensive evaluation method about stability of polylaminate goafs[J]. Journal of Central South University (Science and Technology) , 2012, 43(6): 2324−2330.

[11] 李术才, 平洋, 王者超, 等. 基于离散介质流固耦合理论的地下石油洞库水封性和稳定性评价[J]. 岩石力学与工程学报, 2012, 31(11): 2162−2170. LI Shucai, PING Yang, WANG Zhechao, et al. Assessments of containment and stability of underground crude oil storage caverns based on fluid-solid coupling theory for discrete medium[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11): 2162−2170.

[12] 朱永生, 朱焕春, 石安池, 等. 基于离散单元法的白鹤滩水电站复杂块体稳定性分析[J]. 岩石力学与工程学报, 2011, 30(10): 2068−2075.ZHU Yongsheng, ZHU Huanchun, SHI Anchi, et al. Complicated block stability analysis of Baihetan hydropower station based on distinct element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2068−2075.

[13] 张天军, 羽玥, 张磊, 等. 矿山开采沉陷的FLAC3D数值模拟分析[J]. 煤炭技术, 2018(2): 11−14. ZHANG Tianjun, YU Yue, ZHANG Lei, et al. Numerical simulation analysis of mining subsidence of mine by FLAC3D[J]. Coal Technology, 2018(2): 11−14.

[14] 江权, 冯夏庭, 陈国庆. 考虑高地应力下围岩劣化的硬岩本构模型研究[J]. 岩石力学与工程学, 2008, 27(1): 144−152. JIANG Quan, FENG Xiating, CHEN Guoqing. Study on constitutive model of hard rock considering surrounding rock deterioration under high geostresses[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 144−152.

[15] 江权. 高地应力下硬岩弹脆塑性劣化本构模型与大型地下洞室群围岩稳定性分析[D]. 武汉: 中国科学院武汉岩土力学研究所, 2007: 16−29.JIANG Quan. Study on model and stability of surrounding rock of large underground caverns under high geo-stress condition[D]. Wuhan: Chinese Academy of Sciences. Institute of Rock and Soil Mechanics, 2007: 16−29.

[16] 胡盛明, 胡修文. 基于量化的GSI系统和Hoek−Brown准则的岩体力学参数的估计[J]. 岩土力学, 2011, 32(3): 861−866. HU Shengming, HU Xiuwen. Estimation of rock mass parameters based on quantitative GSI system and Hoek−Brown criterion[J]. Rock and Soil Mechanics, 2011, 32(3): 861−866.

[17] 林锋, 黄润秋, 王胜, 等. 岩体体积节理数(J)的现场测量方法评价[J]. 工程地质学报, 2008(5): 663−666. LIN Feng, HUANG Runqiu, WANG Sheng, et al. Evaluation of in-situ measurement methods for counting volumetric joints of rock mass[J].Journal of Engineering Geology, 2008(5): 663−666.

[18] JIN Changyu, YANG Chengxiang, FANG Dan, et al. Study on the failure mechanism of basalts with columnar joints in the unloading process on the basis of an experimental cavity[J]. Rock Mechanics and Rock Engineering, 2015, 48(3): 1275−1288.

[19] 蒋斌松, 蔡美峰, 贺永年, 等. 深部岩体非线性Kelvin 蠕变变形的混沌行为[J]. 岩石力学与工程学报, 2006, 25(9): 1862−1867.JIANG Binsong, CAI Meifeng, HE yongnian, et al. Chaotic behavior of nonlinear Kelvin creep of rock mass in deep ground[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1862−1867.

[20] 伍国军, 陈卫忠, 曹俊杰, 等. 工程岩体非线性蠕变损伤力学模型及其应用[J]. 岩石力学与工程学报, 2010, 29(6): 1184−1191.WU Guojun, CHEN Weizhong, CAO Junjie, et al. Nonlinear creep damage model of engineered rock and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1184−1191.

[21] 董金奎, 冯夏庭, 张希巍, 等. 地下采场破碎岩体稳定性评价与参数优化[J]．东北大学学报(自然科学版), 2013, 34(9): 1322−1326. DONG Jinkui, FENG Xiating, ZHANG Xiwei, et al. Stability evaluation and parameter optimization on the fractured rock mass in underground stope[J]. Journal of Northeastern University(Natural Science), 2013, 34(9): 1322−1326.

Numerical model building for broken ore body and optimization of stope structural parameters

LIU Dong1, SHAO Anlin2, JIN Changyu2, DING Chenggong2, FAN Fuquan2

(1. College of Engineering, Shantou University, Shantou 515063, China; 2. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China)

The −390 m middle segment of Jiaojia Gold Mine was used as the test stope to optimize the approach span of the stope. The geological conditions and mechanical properties of the ore rock were determined byobservations, joints scanning and acoustic wave tests. A numerical simulation model suitable for jointed rock mass was established. The calculation parameters were gained by Hoek-Brown strength criterion and back-analysis. Combined with FLAC3D numerical simulation, six different approach spans were calculated and analyzed. The results show that the displacement of the roof and the volume of the plastic zone increase linearly with the increase of the span when the access span of the stope increases from 3.5 m to 6.5 m. When the stop span exceeds 7.5 m, the displacement and plastic zone volume of stop roof increase sharply with the increase of span, and the surrounding rock has entered the plastic stage. It is determined that the −390 m midcourse approach span is 7.5 m, which can meet the stability requirements of rock mass. The proposed analysis method is proved to be correct and feasible.

rock mechanics; broken orebody; stope span; optimization analysis; numerical simulation

10.11817/j.issn.1672−7207.2019.02.024

TU93

A

1672−7207(2019)02−0437−08

2018−03−26；

2018−05−26

中央高校基本科研业务专项资金资助项目(N170104025)(Project(N170104025) supported by the Fundamental Research Funds for the Central Universities)

金长宇，博士，教授，博士生导师，从事深部岩体与节理岩体力学特性研究；E-mail：jinchangyu@mail.neu.edu.cn

(编辑 伍锦花)