双定子力偶型液压马达与其转子径向受力特性
刘巧燕 闻德生 吕世君 高俊峰
(燕山大学机械工程学院, 秦皇岛 066004)
0 引言
现有液压马达,无论是齿轮式、叶片式(双作用叶片马达除外),还是柱塞式,由于受基本工作原理的限制,马达在一侧输入高压油,一侧排出低压油[1-2]。马达转子在受到高压油驱动力矩的同时,还将受到高压区极大的侧向力,以致马达运动副中存在不平衡力,同时在系统液压脉动的作用下,马达运动副始终处于复杂的交变载荷下,这导致马达零件、标准件(轴承、弹簧)加速疲劳破坏,是马达实际使用寿命短的根本原因[3-5]。
由于径向不平衡力的存在,这就使得在设计液压马达零件时,为了解决液压马达的不平衡力而增加零件的抗弯强度,致使零件的结构尺寸增大,最终会导致液压马达体积大、质量大、比功率小[6-8]。
针对上述问题,并结合目前已对双定子系列新型元件进行的一系列分析与研究[9-21],本文提出力偶原理液压马达,通过原理及结构上的设计,使马达转子、轴、轴承等关键零部件在工作过程中不受不平衡径向力的作用,从本质上改变马达关键零部件的受力状态,以提高其使用寿命。
1 力偶型液压马达定义及分类
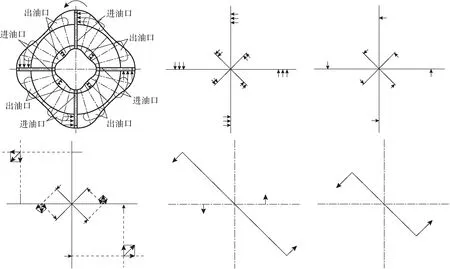
图2 四作用双定子液压马达受力示意图Fig.2 Force diagram of four-acting double-stator motor
力偶原理液压马达在结构上必然为双作用或多作用形式,马达内有多个高压油区及相同数量的低压油区。其中,多作用形式又分为偶数作用与奇数作用的力偶原理液压马达。以偶数作用力偶原理液压马达中的双作用叶片马达为例,如图1所示,通过液压油的作用,其依靠作用在转子上的一个力偶来驱动转子旋转,使得马达的转子受到平衡的径向液压力,从而使叶片马达的旋转部件的受力状况得到改善,进而提高马达的使用寿命。

图1 双作用叶片马达受力示意图Fig.1 Force diagram of double acting vane motor
力偶原理液压马达定义为:液压马达工作时,在垂直于转子轴方向的任意平面内,转子受到的合力为零,但合力矩不为零,形成力偶,此力偶使液压马达产生转矩和转速,这种径向力平衡的液压马达称为力偶原理液压马达。根据不同的作用形式,力偶型液压马达可以分为以下3种不同的类型。
1.1 力偶原理液压马达
力偶——大小相等、方向相反,但作用线不在同一直线上的一对力。力偶能使物体产生纯转动效应,从而消除液压马达中存在的径向不平衡力,现有的双作用叶片马达是力偶原理液压马达的典型结构。
1.2 力偶系原理液压马达
力偶系——作用在同一平面内的多个力偶组成的力偶集合。力偶系使物体产生的纯转动效应与力偶的作用相似,同样可以消除液压马达中存在的径向不平衡力,现有的多作用内曲线径向柱塞式液压马达与四作用液压马达都是力偶系液压马达的典型结构,四作用液压马达的受力示意图如图2所示。
1.3 类力偶原理液压马达
类力偶——两个以上奇数个大小相等、沿等径圆周方向均布的一组力的集合。类力偶虽然不属于力偶和力偶系的概念,但是类力偶对刚体产生的综合作用效果是合力为零、合力矩不为零,与力偶和力偶系的作用效果相同,同样可以消除马达转子中存在的径向不平衡力。双定子三作用叶片马达是类力偶原理液压马达的典型结构,其受力示意图如图3所示。
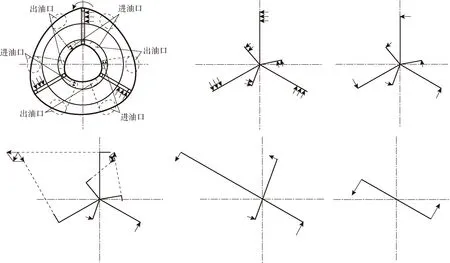
图3 三作用双定子液压马达受力示意图Fig.3 Force diagram of three-acting double-stator motor
2 马达叶片数与力偶的关系
力偶型双定子液压马达中的力偶是由高压区的高压油液作用在多个叶片上产生的,所以探讨力偶与叶片数的关系是提高力偶理论作用效果的关键。
2.1 偶数作用双定子马达的转子径向受力
对于作用数为偶数的双定子液压马达来说,只有当其叶片数为偶数时,由于其高、低压油腔各自成对地对称分布,因此作用于转子圆周上的径向液压力基本平衡,此时转子所受的径向液压力平衡。
双作用双定子偶数叶片在不同工作方式下的高压油液分布示意图如图4所示。由图4可知,双作用双定子液压马达的各高压油腔均对称分布,所以4种不同工作方式下转子所受到的径向液压力基本平衡。
2.2 奇数作用双定子马达的转子径向受力
叶片式马达转子受到的径向力由直接作用在转子圆周上的液压力和作用在封油区叶片上的液压力两部分组成。除了单作用叶片式马达外,处于封油区的叶片均是在大、小圆弧区段的叶片,叶片两侧均受到相同压力油液的作用,而此时叶片所受液压力的方向均沿转子切向方向。因此,对于N(N>1)作用的叶片马达,转子所受径向力只有直接作用在转子圆周上的液压力。
2.2.1每个作用周期内叶片数相同
如图5所示,转子在旋转的过程中,由相邻两个滚柱连杆组与转子、定子、两侧配流装置所组成的密闭容腔的数目也是不断变化的,并且与每个作用周期内的连杆组数也有密切的关系。
(1)叶片数相同且为奇数
由分析可知每个作用周期内由相邻两滚柱连杆组所围成的高压密闭腔的个数为
(1)
式中β0——配油窗口的夹角
β——两相邻滚柱连杆组夹角
z1——一个作用周期内的滚柱连杆组数
φ——叶片1与坐标起始线夹角
在不考虑滚柱连杆组厚度的情况下,单个高压密闭容腔受到高压油作用从而对转子产生的径向液压力分别为:
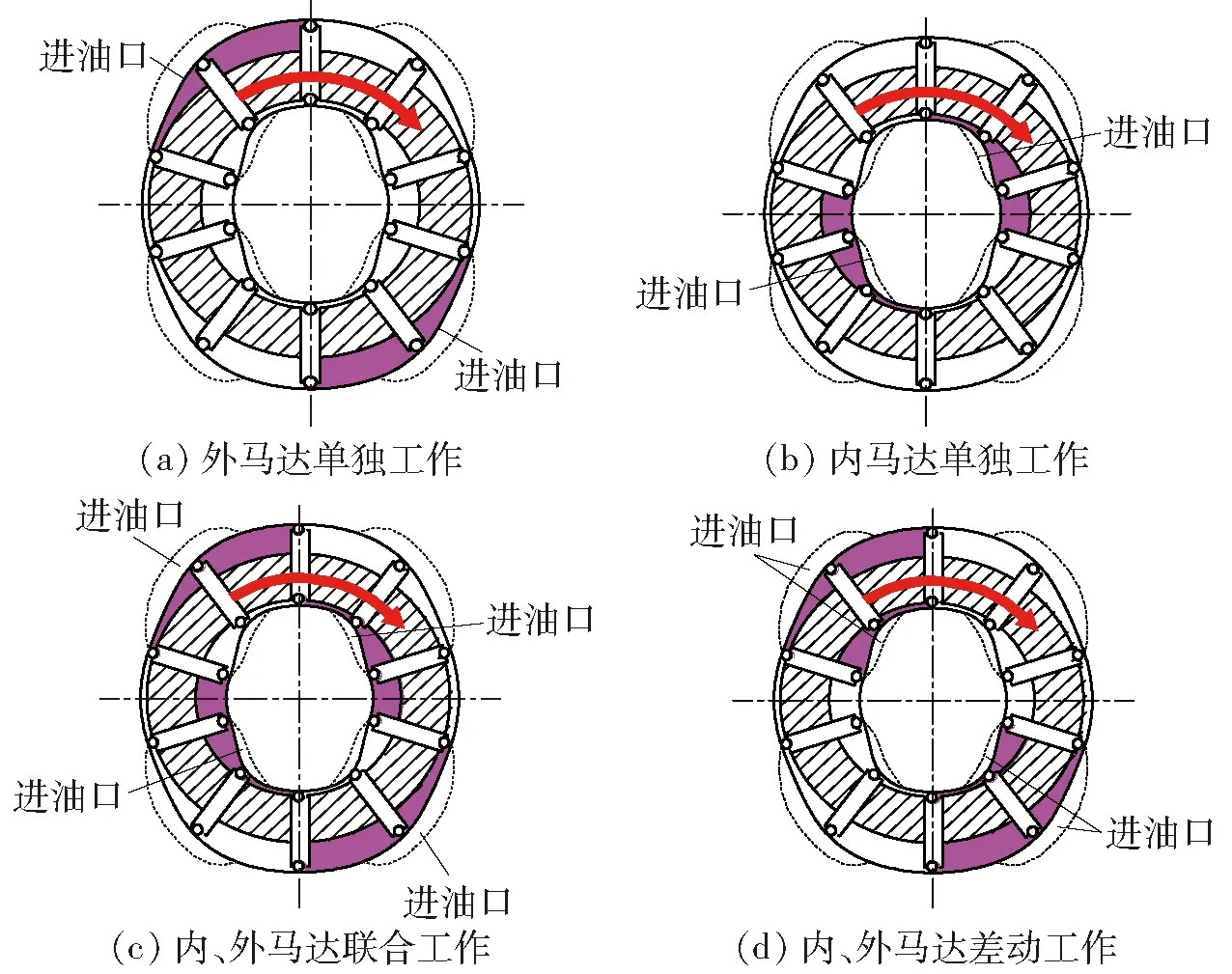
图4 双作用双定子液压马达高压油液分布示意图Fig.4 High pressure oil distribution diagrams of double-acting double-stator hydraulic motor
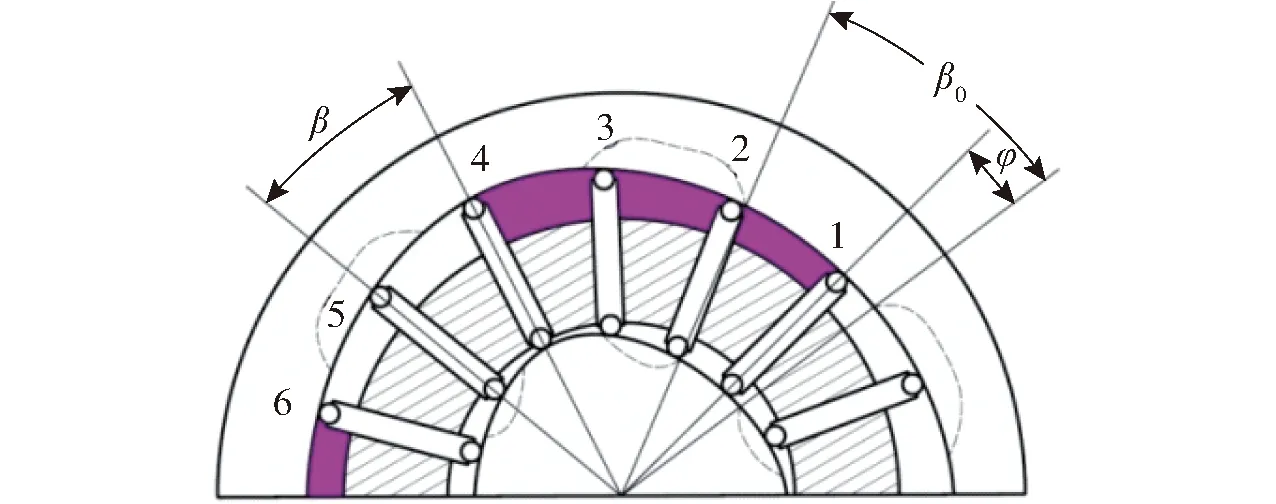
图5 转子径向受力分析简图Fig.5 Radial force analysis diagram of rotor
外马达单独工作
(2)
内马达单独工作
(3)
内、外马达联合工作
(4)
内、外马达差动工作
(5)
式中R——转子外圆半径,mm
r——转子内圆半径,mm
p1——高压油腔油液压力,MPa
B——转子宽度,mm
因此,在一个作用周期内就有M1个这样的径向液压力指向转子圆心,而这M1个径向液压力又可以合成一个指向转子圆心的合力,且此合力与坐标起始线的夹角为
(6)
(2)叶片数相同且为偶数

结合上述两种情况可知,当每个作用周期内的滚柱连杆组数相同,对于N(此时N为奇数)作用的双定子液压马达来说,N个作用周期内就有N个大小相等的径向液压合力沿转子外圆周表面或内圆周表面均匀分布且均指向转子圆心或背离转子圆心。在4种不同的工作方式下,转子在工作的过程中均受到平衡径向液压力的作用。
2.2.2每个作用周期内叶片数不同
以三作用双定子液压马达为例进行分析,当3个作用周期中的1个作用周期内的滚柱连杆组数为z1(令z1为奇数,z1为偶数时的情况与奇数时相同)时,3个作用周期内的滚柱连杆组数的分布有以下4种情况:①2个作用周期内的滚柱连杆组数为z1,1个作用周期内的滚柱连杆组数为z1-1。②2个作用周期内的滚柱连杆组数为z1,1个作用周期内的滚柱连杆组数为z1+1。③1个作用周期内的滚柱连杆组数为z1,2个作用周期内的滚柱连杆组数为z1-1。④1个作用周期内的滚柱连杆组数为z1,2个作用周期内的滚柱连杆组数为z1+1。

外马达单独工作
(7)
内马达单独工作
(8)
内、外马达联合工作
(9)
内、外马达差动工作
(10)

图6 z1取5时三作用双定子液压马达受力简图Fig.6 Force diagrams of three-acting double-stator hydraulic motor when z1 was 5
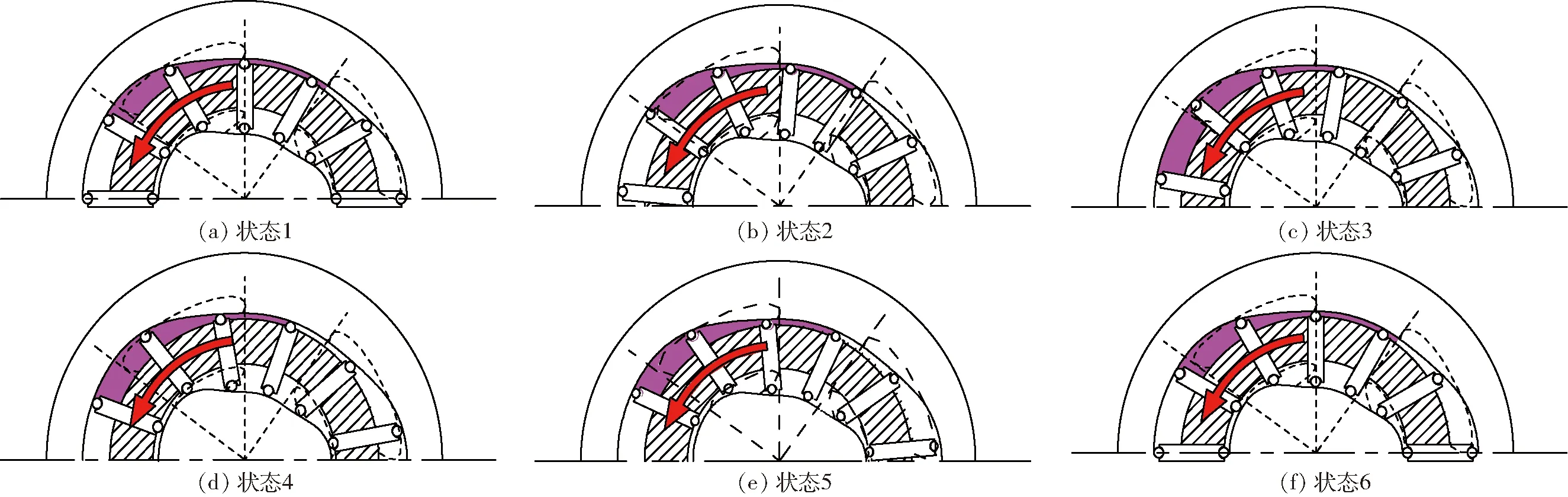
图7 转子周期性受力示意图Fig.7 Periodic force diagrams of rotor
图中各径向力之间的夹角为
(11)
根据各径向力的大小以及作用线的夹角,由分析可知,在4种不同工作方式下转子所受的径向合力不为零,即转子径向受力不平衡,不能称为力偶型液压马达。对另外3种情况采用相同的方法进行分析,也可得相同结论。
3 力偶型双定子马达转子所受径向力
转子是力偶型双定子液压马达中的关键零部件,作为一个旋转部件,其在工作的过程中所受到的径向力的作用不仅对其自身的变形程度有影响,而且还会直接影响轴承寿命,以致于关系到整个液压马达的使用寿命。
当力偶型双定子液压马达运转稳定时,转子所受到的径向力是以两相邻叶片间的夹角为周期变化的,图7为外马达单独工作时一个作用周期内转子受到高压油液作用的分布情况。
双作用双定子力偶原理液压马达的原理简图如图8所示,以叶片1为起点将转子圆周的一个作用周期等分为M个压力分布区,按顺时针方向依次规定为第1压力分布区、第2压力分布区、…、第m压力分布区(1≤m≤M),图中φ1、φ3为高压油区的压力分布区间角,φ2、φ4为低压油区的压力分布区间角。可以得出双定子液压马达外马达单独工作时转子在x、y方向上受到的径向液压力为
(12)
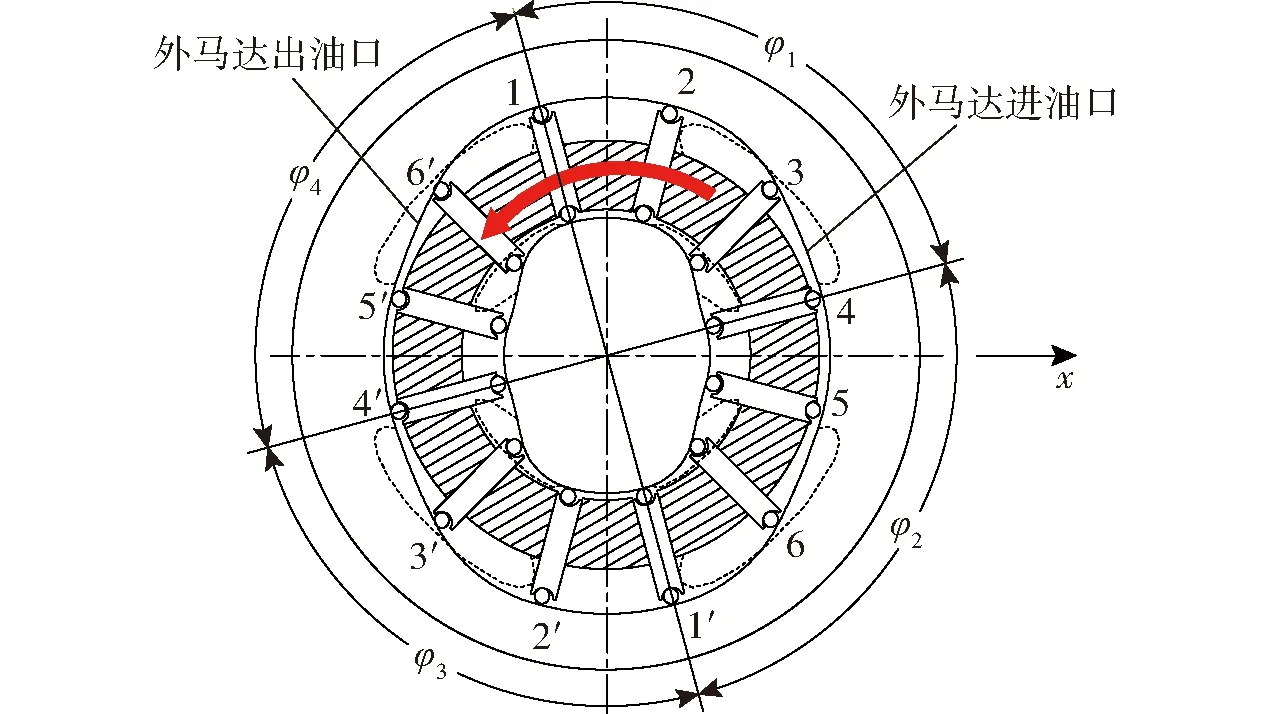
图8 双作用双定子力偶原理液压马达原理简图Fig.8 Schematic of double-acting double-stator couple motor
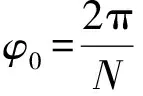
式中p0——高压油液压力,Pa
p——低压油液压力,Pa
关于建设“城市水库”打造“浙中水乡”的调研与思考……………………………………………………… 陈一新(9.7)
其与x轴正向的夹角为
(13)
同理可以得出其他工作方式下转子在x、y方向上受到的径向液压力以及方向:
内马达单独工作时
(14)
(15)
内、外马达联合工作时
(16)
(17)
内、外马达差动工作时
(18)
(19)
4 仿真计算与分析
根据力偶型双定子马达样机(图9)参数对转子的径向受力及方向在一个作用周期内的状况进行仿真计算。样机参数为:额定压力为6.3 MPa;外定子大、小圆弧直径分别为100、91 mm;内定子大、小圆弧直径分别为65、56 mm;转子内、外直径分别为65、91 mm;转子宽度为50 mm。

图9 力偶型双定子马达样机Fig.9 Prototype of double-stator couple motor
由于转子径向受力状况是以两相邻叶片间夹角为周期进行变化的,因此,以图8中叶片2转到叶片1时的过程进行分析,此过程中转子在4种不同工作方式下的径向受力以及力的作用点与水平方向的夹角如表1所示。
图10为力偶型双定子液压马达在单个周期内的转子径向受力变化曲线。对比双定子马达在4种不同工作方式下转子的径向受力状况可知:内、外马达联合工作时转子所受径向力最大,外马达单独工作时次之,内、外马达差动连接工作时转子所受径向力最小,且远小于外马达单独工作与内外马达联合工作时转子的径向受力。


表1 转子所受径向合力及方向Tab.1 Rotor’s radial force and direction

图10 单个周期内转子所受径向力的变化曲线Fig.10 Change of radial force of rotor in a single cycle
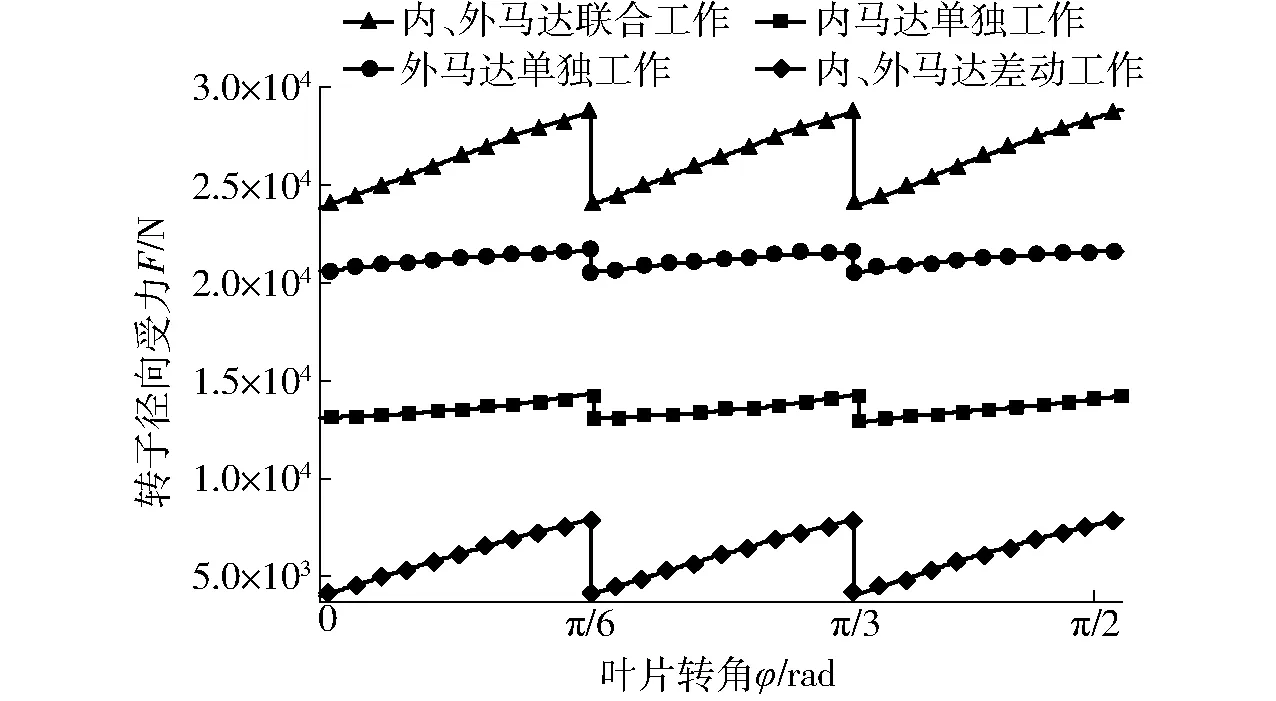
图11 一个作用周期内转子所受径向力的变化曲线Fig.11 Changes of radial force of rotor during one cycle
以此样机为例进行分析,如图12所示,外马达单独工作时,转子径向受力的作用点在29.87°~57.08°(与x轴正向的夹角)之间进行周期性变化;内马达单独工作时,转子径向受力的作用点在-57.41°~-23.54°之间进行周期性变化;内、外马达联合工作时,转子径向受力的作用点在17.34°~48.08°之间进行周期性变化;内、外马达差动连接工作时,转子径向受力的作用点在59.73°~74.80°之间进行周期性变化。
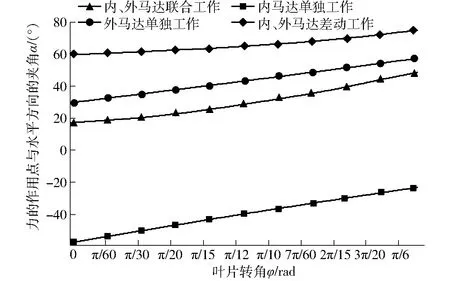
图12 单个周期内转子所受径向力的方向变化曲线Fig.12 Direction of radial force experienced by rotor in a single cycle
5 样机马达实验
为了验证双定子力偶型液压马达原理和结构设计的正确性与合理性,搭建了实验平台,对样机马达在4种不同工作方式下的空载排量及效率进行实验,实验系统原理图及实验测试系统如图13、14所示。
根据实验所得数据可得出双定子力偶型液压马达的效率如图15~17所示。
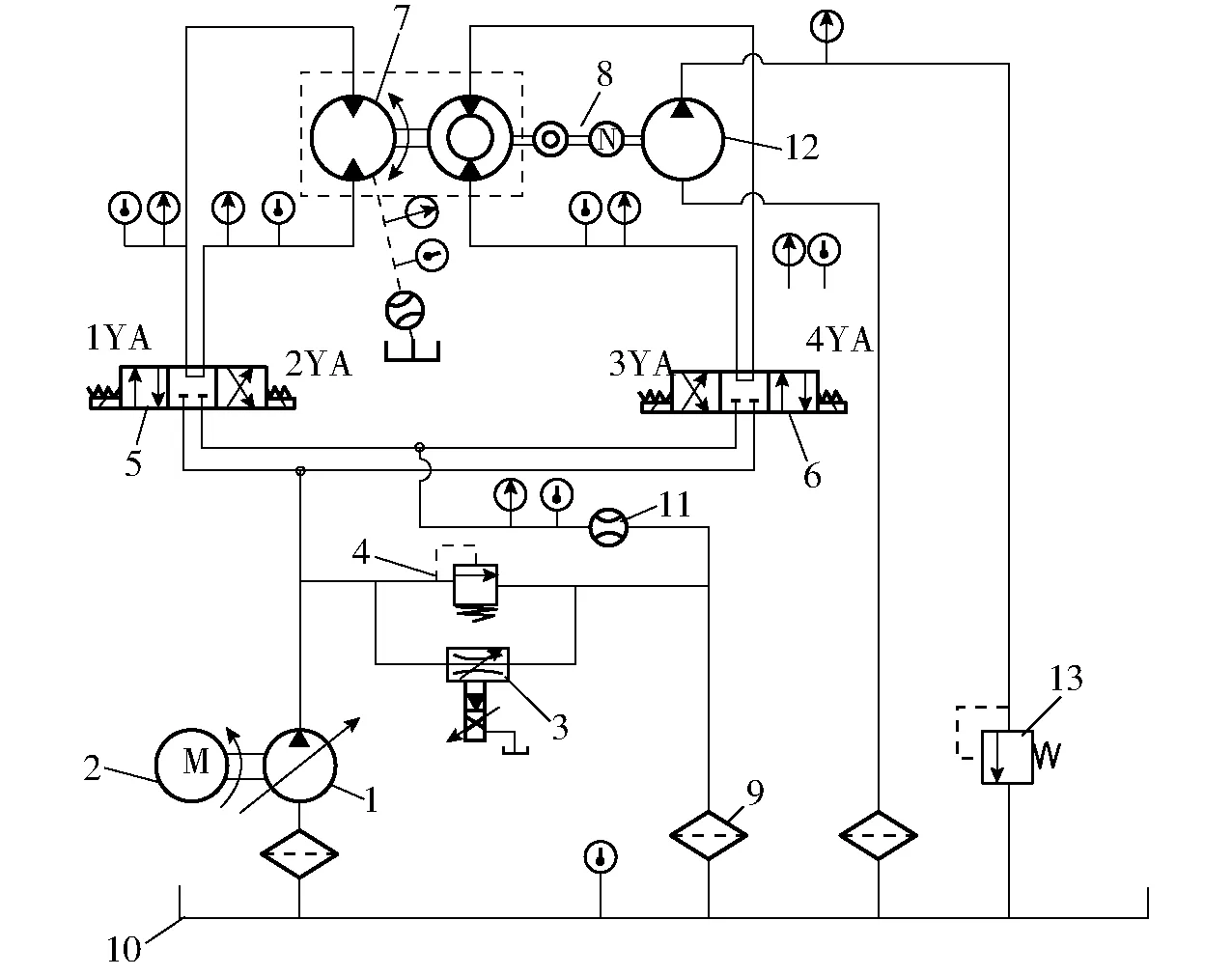
图13 双定子力偶型马达实验系统图Fig.13 Experimental system for double-stator couple motor1.变量泵 2.电动机 3.比例调速阀 4.安全阀 5、6.电磁换向阀 7.被测马达 8.转矩、转速测试仪 9.滤油器 10.油箱 11.流量计 12.负载泵 13.溢流阀

图14 实验测试系统图Fig.14 Picture of experimental test system
由图15~17可得,当内马达单独工作时马达容积效率最大,外马达单独工作时次之,联合工作时最小。而马达机械效率则是联合工作时最大,内马达单独工作时最小。马达总效率随着工作压力的增大而增加。
6 结论
(1)提出了力偶原理液压马达的概念,根据不同的作用形式对力偶原理液压马达进行分类,并对3种不同类型的力偶原理液压马达进行了阐述。
(2)对于偶数作用的液压马达,当叶片数为偶数时,对于奇数作用的液压马达,当叶片数能够被作用数整除时,转子径向受力状况基本平衡,可称为力偶原理液压马达。
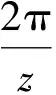
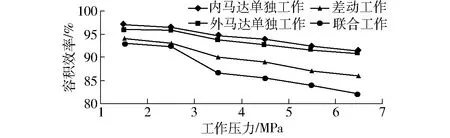
图15 容积效率曲线Fig.15 Volumetric efficiency curves
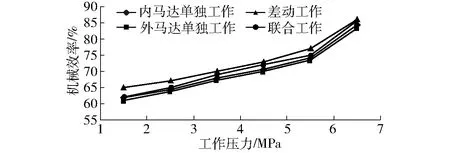
图16 机械效率曲线Fig.16 Mechanical efficiency curves

图17 液压马达总效率曲线Fig.17 Total efficiency curves of hydraulic motor
(4)通过样机实验,验证了双定子力偶型液压马达原理正确性与马达结构设计合理性。

