考虑热力学效应的空化模型修正及其适用性研究

张德胜 万福来 许 彬 王超超 施卫东

(1.江苏大学流体机械工程技术研究中心， 镇江 212013； 2.南通大学机械工程学院， 南通 226019)

0 引言

空化是一种包含湍流、多相流、相变、噪声、可压缩和非定常特性的复杂流动现象[1-3]。近年来，低温介质的运用促进了低温空化的研究。液化天然气等低温介质已经成为我国能源领域迅猛发展的新型产业[4-5]，而其温度为-160℃左右，极容易导致泵内发生空化现象，这对低温介质的空化性能提出了较高的研究要求。由于大部分空化都发生在常温水中，所以通常假设空化过程为等温过程，而低温流体介质物理属性对温度变化敏感，故热力学效应决定低温流体空化流数值模拟的准确性显著[6-7]。

在低温流体空化的数值计算和实验研究方面，STEPANOFF等[8]最早提出了一种B因子理论，用于预测泵中热力学效应对扬程的影响；HORD[9]以液氮和液氢为介质，做了较为全面系统的低温流体的空化实验，进一步加深了对低温空化特性的认识。CERVONE等[10]对不同温度水为介质的NACA0015翼形水翼空化开展了一系列实验研究，分析了热力学效应对其空化特性的影响。王巍等[11]对不同温度水为介质的NACA0066(MOD)翼型开展了翼型表面空化场的流动分析。由于低温流体工作环境的限制，极大增加了实验的难度。近年来，数值计算成为研究低温流体空化的重要手段，HOSANGADI等[12]采用Merkle空化模型对液氢和液氮绕翼型空化流动进行了模拟计算，但模拟结果与实验对比误差较大。为了提高数值模拟预测精度，TANI等[13]在B因子理论基础上提出了一种新的空化模型，通过与实验数据相比较确定了空化模型的蒸发凝结系数，使得计算结果较为吻合。国内学者也对低温流体空化做了一些研究[14-16]，评价了不同空化模型对低温空化的数值计算情况，并改进了个别空化模型，使得数值计算结果与实验数据更为接近，但这些研究都是二维翼型的数值模拟计算。因此，本文重点开展三维翼型考虑热力学效应的空化模型改进和验证研究。

本文通过CFX前处理编辑，将3种典型空化模型嵌入CFX软件中，并将水、液氮热传导系数以及饱和蒸汽压强等随温度变化的物性参数引入到求解代码程序。 同时考虑空化过程汽化潜热的影响，并在B因子理论的基础上，提出一种空化模型的修正方法。采用原始的和修正的空化模型，计算水及液氮绕翼型的空化流动，并与实验结果进行对比，评估不同空化模型对空化流动的热力学效应的敏感性和修正的空化模型的适用性，为开展低温空化研究提供理论支撑。

1 控制方程与数值方法

1.1 基本方程

对于考虑热力学效应的空化流动问题数值计算的控制方程，除了连续性方程和动量方程外，还包括包含能量源项的能量方程，依次为

(1)

(2)

(3)

式中ρm——混合相密度p——压强

μ——混合介质的动力黏性系数

keff——热传导系数

L——汽化潜热

Cp——定压比热容

fv——气相的质量分数

T——温度t——时间

xi——x在i方向分量

xj——x在j方向分量

δij——克罗内克函数

ui、uj——速度在i、j方向分量

μt——湍流粘度

1.2 湍流模型

计算采用了由MENTER[17]提出的SSTk-ω两方程湍流模型，公式为

(4)

(5)

涡黏系数计算公式为

(6)

式中ρ——密度k——湍动能

ω——湍流频率

σk3、σω2、σω3、α3、β3、β′——湍流模型常数

F1、F2——混合函数

S——剪切力张量的常数项

Pkb——浮力湍动能生成项

Pk——粘性力湍动能生成项

Pωb——湍流模型自定义项

a1——湍流模型常数

湍流模型常数取值参照文献[18]。

1.3 空化模型

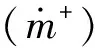
(7)

式中u——速度矢量

αv——气相体积分数

ρv——气相密度

1.3.1Zwart空化模型

Zwart空化模型[19]是基于单个空泡的生成和发展时空泡体积的变化，基于Rayleigh-Plesse空泡生长方程推导出的蒸发源项和凝结源项表达式

(8)

(9)

式中RB——平均空泡半径，取1×10-6m

ρl——液相密度pv——气相压力

αnuc——气核体积分数，取5×10-4

Fvap、Fcond——蒸发、凝结系数，取50、0.01

1.3.2Merkle空化模型

Merkle空化模型[20]是基于汽液两相流模型，由混合密度导出相间质量传输率，公式为

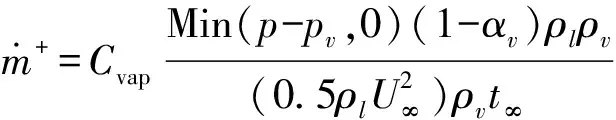
(10)

(11)

式中U∞——参考速度

t∞——参考时间

经验系数Cvap、Ccond分别取1、80。

1.3.3Singhal空化模型

Singhal空化模型[21]是基于汽液两相流模型，综合考虑了空泡在相变过程中表面张力和非凝结性气体的影响，公式为

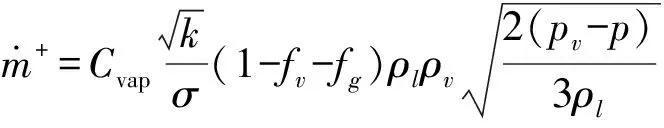
(12)

(13)

式中fg——非凝结气体的质量分数，取10-8

σ——液体表面张力系数

经验系数Cvap、Ccond分别取0.02、0.01。

1.4 空化模型的修正方法

在上述空化模型中，通常认为质量传输只由液相和气相的压力差来驱动，但在高温水和低温液体中，发生空化时，液体汽化吸收汽化潜热，导致空泡附近液体温度降低，从而形成空泡外的薄液体边界层，假设泡内的气体温度是均匀的，其压力等于饱和压力，温度等于饱和压力对应下的饱和温度[13]，由于热力学边界层的存在，泡内和泡外形成了一温度差ΔT，则相变的热平衡公式为

ρvυvL=ρlυlCplΔT

(14)

式中υv、υl——气相、液相的体积质量流量

Cpl——液相的定压比热容

B因子方法[22]及理想气液混合时B因子的表达形式为[23]

(15)

式中B——无量纲因子

国内外化工行业常用的纯液体饱和蒸汽压的三参数方程Antoine方程[24]为

lgpsat=a-b/(T+c)

(16)

式中a、b、c——Antoine常数，取值参照文献[23]

psat——液相饱和蒸汽压力

假定空泡周围热力学状态保持为饱和状态，则可得由于潜热传递而形成的局部饱和蒸汽压的变化ΔpL，其公式为

(17)

除此之外，研究表明湍动能对空化产生重要的影响[24],采用文献[24]中所提出的方法来计算湍动能k对当地汽化压强的影响，其公式为

Δpturb=0.195ρmk

(18)

式中 Δpturb——湍动能引起的压力变化量

基于以上分析，可对1.3节中3个空化模型中蒸发源项和凝结源项就考虑热力学效应的影响进行修正,从而可得

pv=psat+ΔpL+Δpturb

(19)

2 不同温度水的空化流数值模拟

2.1 计算区域及边界条件

为了评估各空化模型的热力学修正效果，首先对以不同温度水为介质的NACA0015翼形的空化流场进行了模拟计算，并与CERVONE等[10]的实验值进行比较。翼型尺寸与计算域选取与实验条件保持一致，如图1所示。设置边界条件：进口给定速度与温度，出口为平均静压；壁面为无滑移绝缘壁面条件。为更准确地计算空化流场，采用结构网格，并在翼型近壁面区域进行网格加密，使分子到最近壁面的无量纲距离y+为10～50之间，大多数学者认为y+值不超过60[25]，则计算y+值满足壁面函数要求，如图2所示。为了对计算所用网格进行验证，本文选取了3套网格，分别模拟计算了无空化流场，如图3a所示。所得压力系数pc与实验值[10]进行对比验证，其中Lc为翼型长度百分数。可知计算所得压力系数与实验较为接近,如图3b所示，并考虑计算经济性，选取方案2进行后续的计算。不同方案的网格信息如表1所示，计算工况见表2。

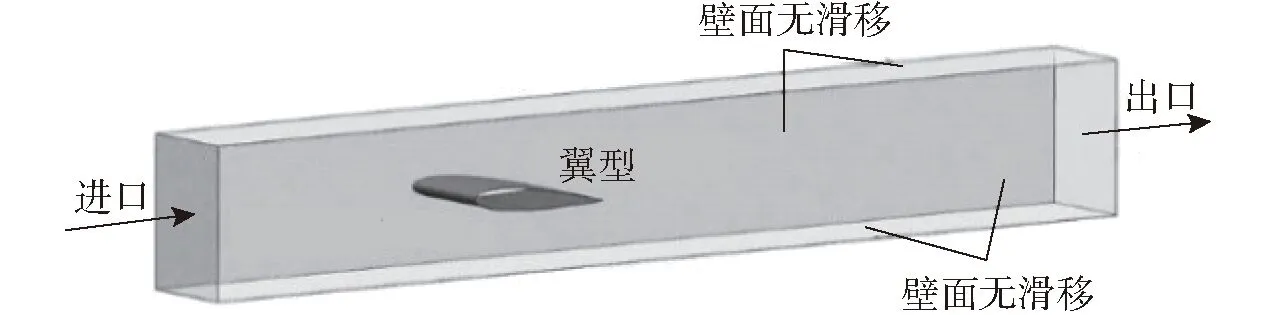
图1 三维水体模型及边界条件Fig.1 Schematic of 3D model with water and boundary conditions of cases

图2 NACA0015翼型网格分布Fig.2 Grids distribution near NACA0015 hydrofoil

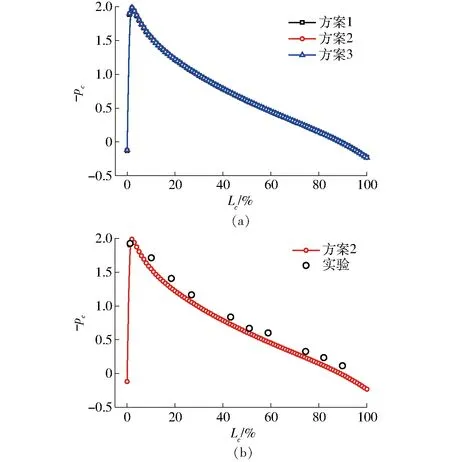
图3 NACA0015网格无关性验证Fig.3 Verification of NACA0015 mesh independence

计算中采用的无量纲参数为无穷远处空化数σ∞、当地空化数σc、压力系数pc、当地空化数与无穷远处空化数之差σ，分别定义为

(20)

(21)

(22)

σ=σc-σ∞

(23)

式中pout——无穷远处压力

T∞——无穷远处温度

uin——进口速度Tc——当地温度

pv(Tc) ——温度为Tc时的饱和蒸气压力

pv(T∞) ——温度为T∞时的饱和蒸气压力

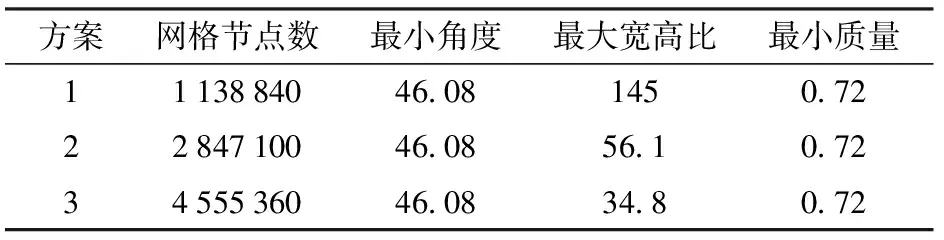
表1 网格信息Tab.1 Information of different grids

表2 不同温度水空化数值模拟边界条件Tab.2 Boundary conditions of numerical simulation about cavitation in water at different temperatures

2.2 计算结果与讨论

为了分析修正空化模型在不同温度水中空化数值模拟中的应用情况，分别运用1.4节中考虑热力学效应修正的Zwart、Merkle及Singhal 3种空化模型，并对298、323、343 K温度水绕NACA0015翼型空化进行了数值模拟研究，并与实验[8]所得翼型吸力面的压力系数分布进行对比分析，如图4所示。结果表明，在3种温度下，修正前后Singhal模型及Zwart模型模拟所得翼型吸力面压力系数分布无明显差别。温度为298 K和323 K时，水的热力学效应比较稳定，压力随温度变化梯度较小，3种空化模型修正前后的模拟结果差异较小。而修正的Merkle模型在水温为343 K所模拟的结果表现出较强的修正效果，修正前后有较明显差别。修正Merkle模型数值模拟得到的翼型吸力面低压区范围较之未修正前的模拟结果均有所增加，对应压力有所降低，并随温度的增加，降低得越多，体现出不同温度水中空化吸收潜热，引起饱和蒸汽压强不同程度降低的热力学效应作用，且越靠近临界温度，其敏感度越高。而同时对应空穴闭合区压力变化梯度均明显增大，且随温度的增加，其压力变化梯度也随之增大，从而更加接近于实验值。

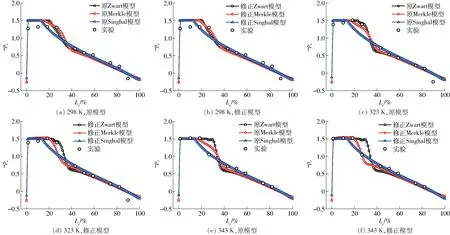
图4 不同温度下不同修正空化模型模拟得到的NACA0015翼型吸力面压力系数分布Fig.4 Pressure coefficient distribution on suction surface of NACA0015 hydrofoil

3 不同温度液氮的空化流数值模拟

3.1 计算区域及边界条件

HORD[9]针对不同温度液氮绕水翼空化进行了较为全面系统的低温流体空化实验研究，其实验段及水翼结构如图5和图6所示。

通过三维造型生成与实验所对应三维水翼，并根据实验中实验段的尺寸进行了实验流道的建模。

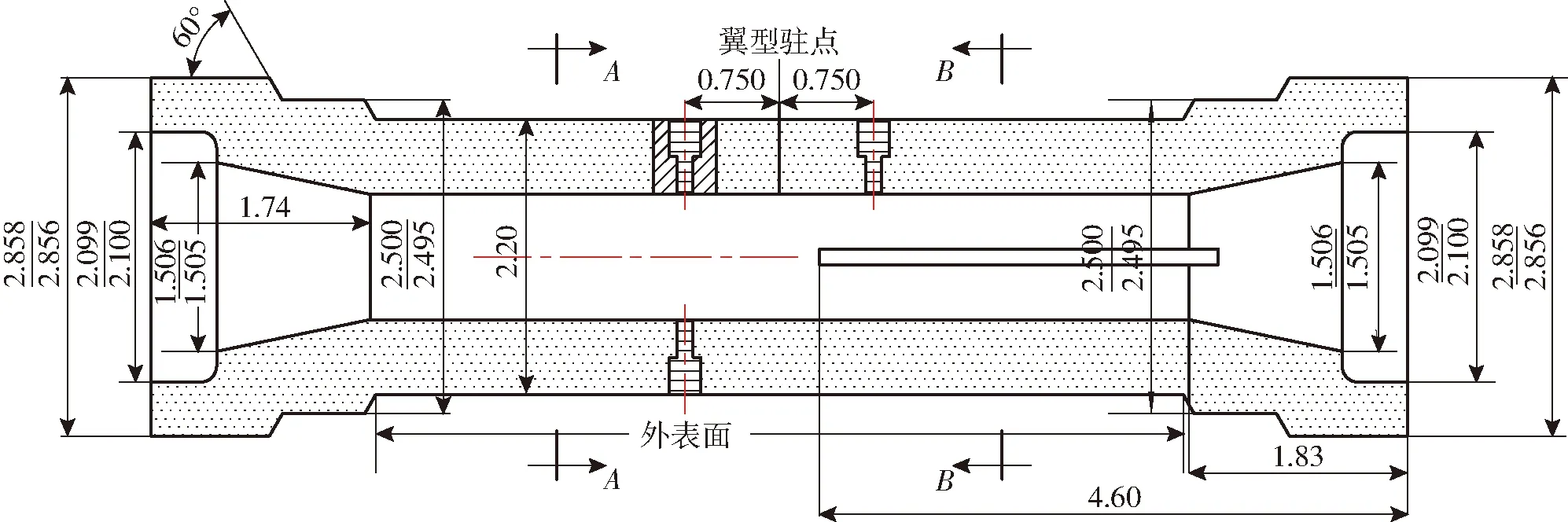
图5 实验段结构Fig.5 Test section structure

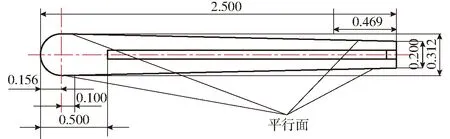
图6 HORD水翼结构图Fig.6 Diagram of hydrofoil structure

同时由于其对称性结构，在数值模拟过程中可进行对称边界条件的设置，故只构建了一半的对称水体模型。三维对称水体模型结构如图7所示。考虑与实验的一致性，进口设置为压力进口，其静压与实验对应进口压力相一致，来流温度根据实验进口所测的温度来设置；出口设置为速度出口，其速度与实验保持一致，边界条件如表3所示。为精准地模拟计算空化流场，在ICEM 软件中进行六面体结构网格的划分，考虑到水翼前缘的圆头形状的影响，采用C型结构化网格，在水翼近壁面区域进行网格加密如图8所示。选取3套网格计算液氮温度83.06 K时翼型表面压力系数分布情况，如图9a所示,各方案网格信息如表4所示。模拟所得压力系数与实验值[9]进行比较，如图9b所示。考虑数值计算的准确性与经济性，选择方案2作为后续模拟计算网格。

图7 三维对称水体模型及边界条件Fig.7 Schematic of symmetrical 3D model with water and boundary conditions of cases

3.2 计算结果与讨论

为了分析不同空化模型在低温流体空化数值模拟中的应用情况，分别运用Zwart、Merkle及Singhal空化模型，采用等温isothermal的流场热传输模式，分别对83.06、77.64 K两种不同温度液氮绕水翼的空化进行数值计算模拟研究，并与HORD的实验数据[9]进行对比分析，所得水翼表面的压力分布如图10所示。在两种液氮中，3种模型模拟所得低压区压强保持为对应远场温度下的饱和蒸汽压强不变，且均大于实验值，说明液氮中热力学效应明显，不容忽视，其中空化与常温水中不同，不能假设为等温过程。而模拟所得低压区范围差异较大，Merkle模型模拟结果较为接近实验值，而Zwart模型与Singhal模型两者模拟结果相近均偏离实验值较多，过多地预测了低压区即空化区域的范围。

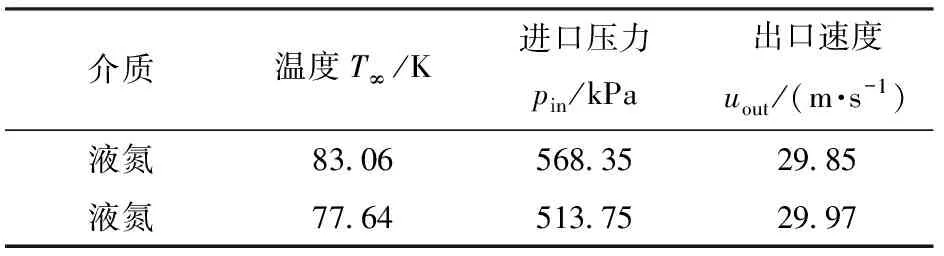
表3 不同液氮中空化数值模拟边界条件Tab.3 Boundary conditions of numerical simulation about cavitation in nitrogen at different temperatures

图8 HORD翼型网格分布Fig.8 Grids distribution near HORD hydrofoil

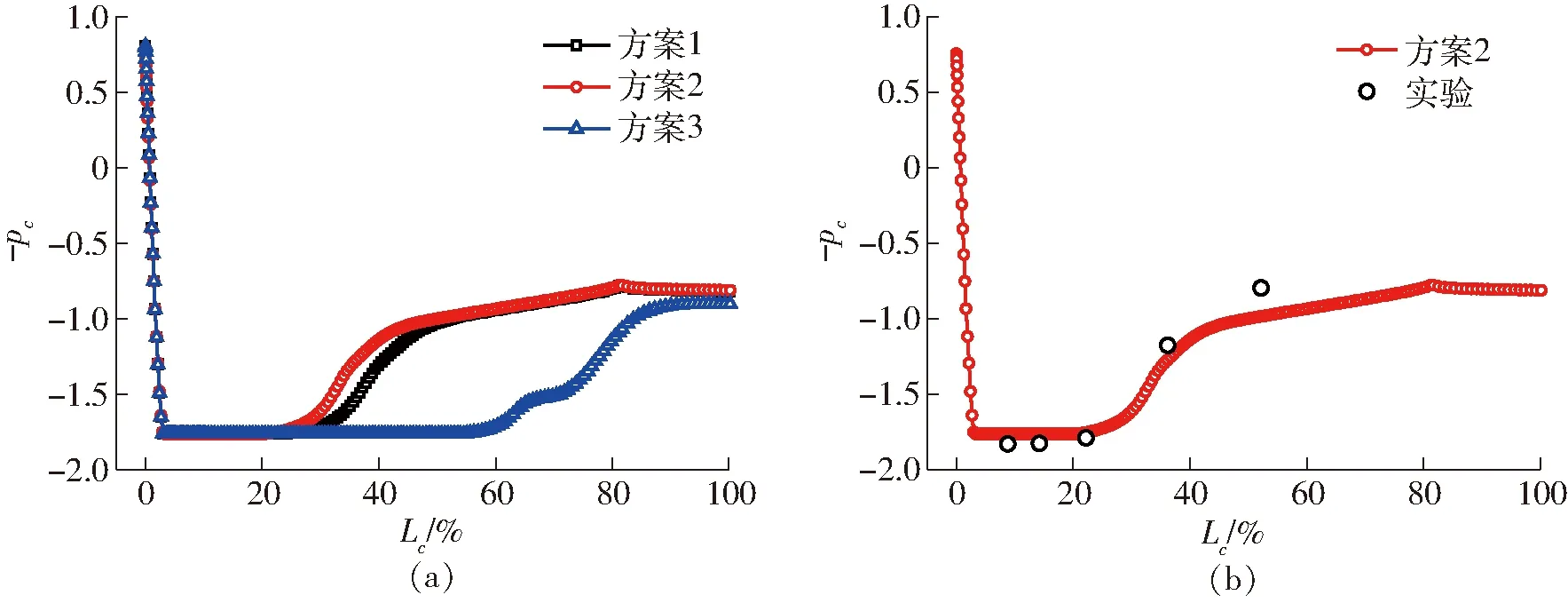
图9 HORD翼型网格变化Fig.9 Changes of HORD hydrofoil mesh

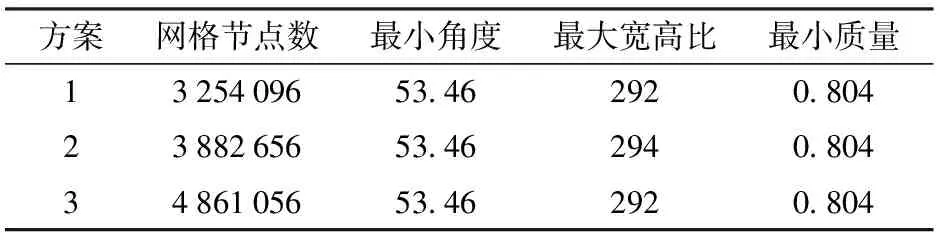
方案网格节点数最小角度最大宽高比最小质量1325409653.462920.8042388265653.462940.8043486105653.462920.804

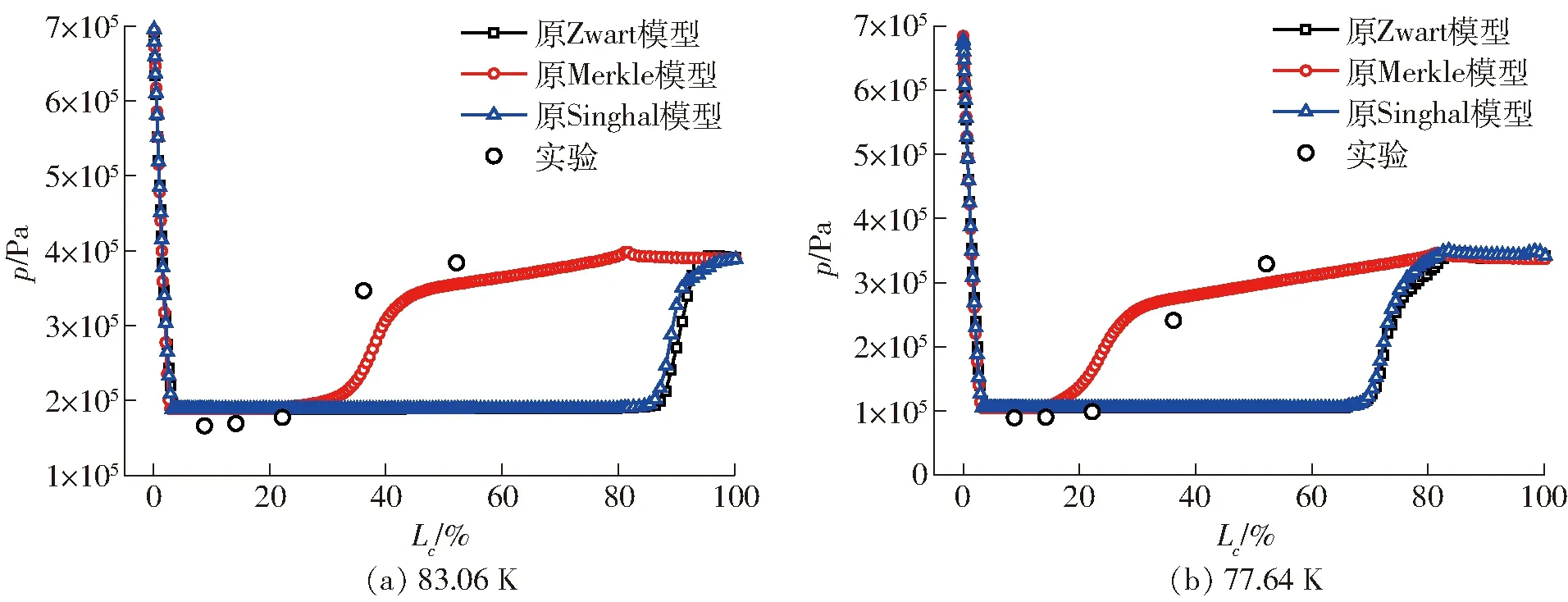
图10 空化模型模拟所得HORD水翼表面的压力分布Fig.10 Pressure distribution on surface of HORD hydrofoil with different cavitation models

综合上述分析可知，Merkle模型在低温流体空化数值模拟中有较好的可行性，其与实验吻合度较为接近。为了分析修正空化模型在不同温度液氮空化数值模拟中的应用情况，运用考虑热力学效应修正的Merkle模型，分别对83.06、77.64 K两种不同温度液氮绕水翼的空化进行数值计算模拟，并与实验数据进行对比分析，所得水翼表面的压力分布如图11所示。结果表明，修正前后Merkle模型所模拟的结果有较明显差别，修正的Merkle模型模拟所得水翼表面低压区范围较之未修正前的模拟结果均有所减小，低压区压力有所降低，且83.06 K中降低量较77.64 K下更多，使得两者模拟结果更加吻合实验低压区压力，这体现出低温流体中空化吸收潜热，引起饱和蒸汽压强不同程度降低的热力学效应作用，也进一步说明了越靠近其临界温度，其敏感度越高。

图11 修正空化模型数值模拟所得HORD水翼表面的压力分布Fig.11 Pressure distribution on surface of HORD hydrofoil with modified cavitation model

采用考虑热力学效应修正及等温模式的Merkle模型模拟所得蒸汽体积分数分布情况，如图12所示，图中y轴表示翼型绝对尺寸，x轴表示翼型相对尺寸。结果表明，等温模式下，无热力学效应作用，空穴区域内的压强恒定为对应远场温度下的饱和蒸汽压强，并且83.06 K中对应远场空化数为1.706，而77.64 K中为1.765，故在83.06 K中的空化区域大于77.64 K的，其空穴长度明显较长。而考虑热力学效应时，局部的温降，导致饱和蒸汽压强的降低，从而降低了空化强度，使得空化区域的蒸汽体积分数减小，空穴长度明显缩短。

根据当地空化数σc的定义，为了更好地表征热力学效应在低温流体空化中的影响，计算了两种液氮中，修正Merkle模型模拟所得空化流场的当地空化数与无穷远处空化数之差σ分布情况，如图13所示。考虑热力学效应时，当地空化数最大的区域与最大压降区、最大温降区相对应，都在空化核心区域，其当地空化数均大于相应的远场空化数，由此与等温模式下相比，考虑热力学效应时的空化强度降低。

图12 不同液氮中模拟所得HORD水翼表面蒸汽体积分数云图Fig.12 Vapour volume fraction on surface of HORD hydrofoil simulated in different liquid nitrogen

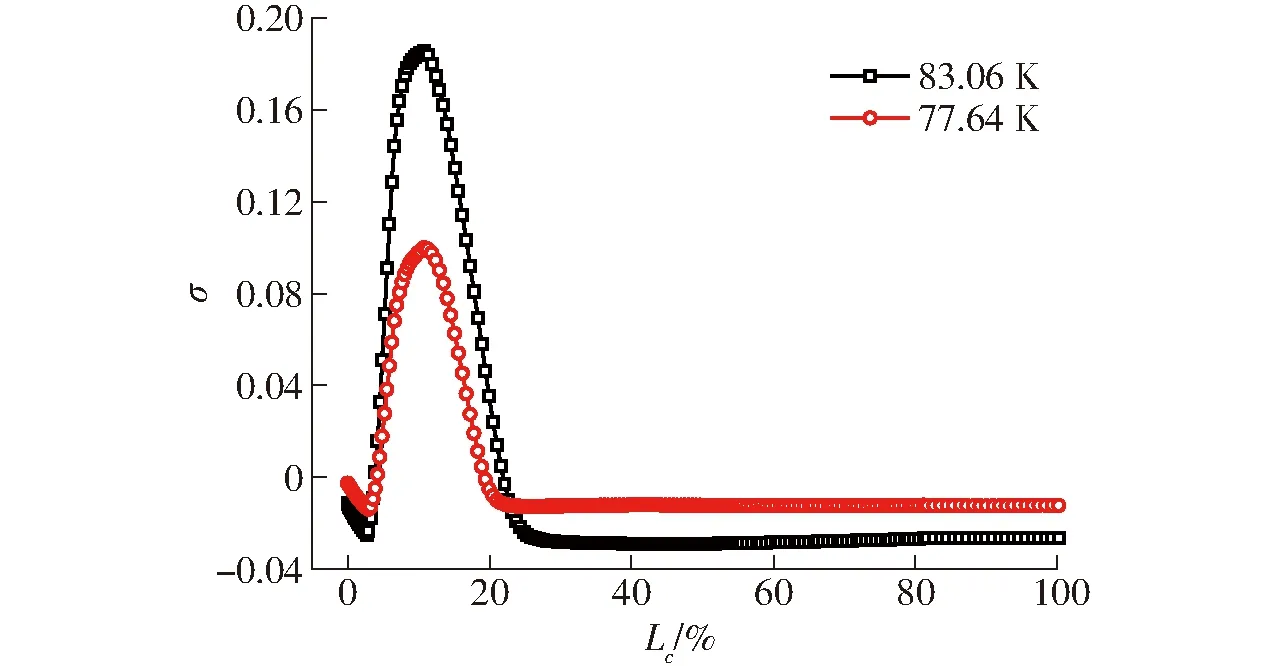
图13 不同液氮中模拟所得HOAD水翼表面σ分布云图Fig.13 Distribution nephogram of σ on surface of HORD hydrofoil simulated in different liquid nitrogen

4 结论

(1)采用Zwart、Merkle及Singhal共3种空化模型及对应修正后的空化模型,分别对3种温度水进行数值模拟，并与实验进行对比，结果表明修正的Merkle模型能更好地体现热力学效应对空化的影响。

(2)采用3种空化模型分别数值模拟83.06、77.64 K两种液氮绕水翼空化流场，并与实验数据进行了对比，发现Merkle模型数值模拟结果与实验值较为接近，适用性相对较强。考虑热力学效应修正的Merkle空化模型，对两种不同温度液氮中空化进行了数值模拟研究，并与实验所得水翼表面压力分布数据进行对比分析，再次验证了修正空化模型的适用性及空化模型修正方法在低温流体空化数值模拟中的可行性。

(3)在修正Merkle模型数值模拟结果的基础上，与等温模式的数值模拟结果相对比，其空化区域由于温降的产生，使得对应饱和蒸汽压强有所降低，致使空化强度减弱，空穴长度缩短，当地空化数均大于远场空化数。且相比77.64 K，83.06 K的温度较高，对于热力学效应的敏感性更高，其空化区域较多的压降使其热力学效应更显著，空化受到抑制作用更明显，空穴缩短更多，空化区域蒸汽体积分数降低更多。