滑动及侧滑影响下的移动机器人轨迹跟踪控制
卫荣慕, 金世俊
(东南大学 仪器科学与工程学院,江苏 南京 210000)
0 引 言
近几十年,由于移动机器人具有非完整约束的性质[1,2],其运动控制研究具有一定挑战性。如实际环境工作中,道路湿滑、结冰、快速转弯等原因,移动机器人不可避免地产生侧滑和滑动,破坏非完整约束[3,4]。为了解决这个问题,文献[5]研究了运动学模型下的纵向滑动参数未知的轨迹跟踪,设计了补偿纵向滑动的自适应非线性反馈控制律,并利用极点配置在线调整控制增益。文献[6]提出基于函数逼近技术的自适应控制方法,利用神经网络补偿干扰观测器估计的误差。文献[7]设计了基于广义扩展状态观测器的鲁棒追踪控制器,实现干扰的衰减和轨迹的准确跟踪。文献[8]提出非线性扰动观测器的滑膜控制器,利用运动学模型导出的偏移模型设计出控制器。文献[9]设计了自适应抗干扰控制器,将滑动和侧滑以及其他扰动视作系统的整体扰动,设计出自适应律,实现机器人轨迹跟踪。但上述文献中的控制设计需要精确的机器人控制模型,且文献[5,8]只考虑到运动学部分,这在移动机器人的工程实际中往往不易实现。
针对上述问题,本文提出了基于动力学的自适应模糊控制方法来解决动力学部分所受到的滑动和侧滑影响。结合H∞控制理论,引用鲁棒补偿项[10]将建模误差,外部干扰包括滑动和侧滑衰减到预先规定的指标,通过Lyapunov方法给出了自适应律。运动学部分是通过逆运动学方法[11]设计的逆运动学控制器,处理受滑动和侧滑影响的实际位置与期望位置的误差,最后以仿真验证了在滑动及侧滑影响下,移动机器人能够准确快速跟踪期望轨迹。
1 数学模型的建立
本文研究的对象为差分驱动轮式移动机器人,结构如图1所示。轮式移动机器人的动力学模型为[6]
(1)
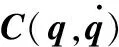

图1 轮式移动机器人结构
由于地面的湿滑和快速转弯,移动机器人容易发生滑动和侧滑,故很难满足理想的非完整性约束条件[11]。因此在发生滑动或侧滑影响下的非完整约束条件为
(2)
式中μ为侧滑速度,ζ=[ζrζl]T为左右驱动轮的滑动引起的干扰角速度。
整理式(2)可知移动机器人在滑动和侧滑影响下的运行速度为
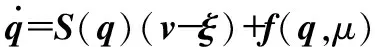
(3)
式中v=[uω]T,u为移动机器人前进的线速度,ω为移动机器人角速度,ξ=[ξuξω],ξu为纵向滑移速度,ξω为偏航角速度。f(q,μ)为扰动非完整约束引起的不匹配干扰向量。
由式(1)和式(2)可知受滑动和侧滑影响的动力学模型
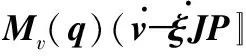
F2(q)f(q,μ)=τ+τd
(4)
式中Mv=(STB)-1STMS,Cv=(STB)-1ST(M+CS),F1=(STB)-1STM,F2=(STB)-1STC。
定理1将输入扰动和移动机器人的滑动、侧滑均视为扰动

(5)
移动机器人的动力学模型可以整理为
(6)

2 逆运动学控制器和自适应模糊动力学控制器设计
2.1 逆运动学控制器设计
逆运动学控制器[11]处理移动机器人实际位置与期望位置之间的误差,输出控制移动机器人运动的期望速度。
令轮式移动机器人的位置坐标为h=[x,y]T,则=Qv,其中

(7)

(8)
式中 [uc,ωc]T为运动学模型的期望速度,Ix,Iy为饱和常数,坐标误差增益kx>0,ky>0。
2.2 自适应模糊动力学控制器设计
本文提出基于动力学的自适应模糊方法[2]控制器,不需要辨识或估计动态模型参数。
受滑动和侧滑影响的移动机器人动力学模型可以写为
(9)
式中z为状态向量,k为输入向量,ε为扰动量,P(z)和Γ(z)为模糊近似函数。
如图2,设计自适应模糊控制器的目的是发现输入力矩τ(t)控制实际速度v(t)渐近收敛到期望速度vc(t)。

图2 控制算法结构
动力学误差为
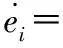
(10)
模糊系统
(11)
为设计未知参数ksi,Pi,Γi的自适应更新率。设计李雅普诺夫函数为
(12)
式中φi,γP,γΓ为正数。

(13)
假设φi满足
(14)
式中ρ,γ,η为正数,则
(15)
此外必须满足式(16)保证式(14)的一个解φi为正数
(16)
不等式(15)是H∞指数[10],因此利用控制律和自适应律可以保证(vc-v)→0。
2.3 完整控制系统稳定性证明
将运动学部分和动力学部分级联后,运动学部分变为
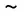
(17)
式中δ为速度控制偏差造成的系统位置控制的偏差

(18)
3 仿真分析
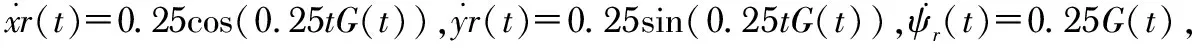
设轮式移动机器人初始姿态(x,y,4)为(0.5,0.5,0)。选取运动学控制器的参数为kx=ky为1,lx=ly为0.1。选取动力学控制器的参数为γ为0.1,γΓ为0.09,γP为0.9,φ1为10,φ2为5,α1为0.1,α2为1。扰动量[ζrζlμ]T和τd分别为[sin(t) cos(t)F(t)]T和[2sin(t) 2cos(t)]T。其中,F(t)=20[U(t-21)-U(t-23)]+24[U(t-37)-U(t-39)]为侧滑量,U(t)为单位阶跃函数。
利用MATLAB/SIMULINK进行仿真分析,将本文提出的自适应模糊动力学控制器与文献[9]自适应控制方法动力学控制器进行对比。
1)由图3(a)可知移动机器在没发生侧滑,只受滑动影响时,能够准确跟踪轨迹。在前两个转弯处同时受滑动和侧滑影响时能够迅速恢复行驶到期望轨迹上。由图3(b)可知在前两个转弯处受滑动和侧滑影响下,轨迹跟踪误差较大,且不能迅速恢复轨迹跟踪。在第三个转弯处只有滑动存在,也不能准确进行轨迹跟踪。

图3 轨迹跟踪对比
2)从图4可知,在21~23 s和37~39 s时受侧滑影响,2种方法控制的轨迹跟踪误差都变大,但是自适应模糊控制的轨迹跟踪误差较小,且能够迅速跟踪到期望轨迹上。

图4 不同方向轨迹跟踪误差
3)从图5可知,自适应模糊控制在发生侧滑时,机器人线速度和角速度跟踪误差较大,但侧滑因素消失后,两速度跟踪误差渐近于零。而自适应控制在没有侧滑影响时也出现周期性误差。
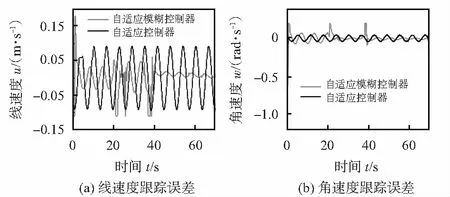
图5 速度跟踪误差比较
4 结 论
1)根据移动机器人受滑动及侧滑影响下的非完整性约束条件,构造出移动机器人的动力学模型。并推导出新的控制系统状态方程。在运动学部分,设计逆运动学控制器,得到移动机器人的期望速度。
2)提出了在滑动和侧滑影响下,基于动力学的自适应模糊控制。通过模糊系统逼近动力学控制系统的未知非线性,H∞对滑动和侧滑干扰的补偿,设计出模糊系数的自适应律,解决移动机器人偏离期望轨迹的问题。
3)仿真表明:本文所提方法有效补偿了滑动和侧滑引起的扰动,使移动机器人在滑动和侧滑的影响下,能够有效进行轨迹跟踪。

