基于惯性姿态参量量化融合的机器腿仿生步态控制*

陆兴华, 黄伟鹏, 黄澎奋

(广东工业大学 华立学院,广东 广州 511325)

0 引 言

仿生机器腿行走步态运动控制[1]过程中,容易受到仿生机器腿的转向部件、活动关节以及周边环境信息的影响,导致步态稳定性不好,定姿能力不强,对此,相关文献进行机器腿步态控制,常见的如模糊比例—积分—微分(proportional-integral-differitional,PID)控制方法、自适应卷积控制方法、Kalman滤波控制方法等[2,3],结合仿生机器腿的行为姿态参量融合和自适应处理实现机器腿的步态控制,文献[4]中提出一种基于连续体模型的蛇形机器人质心速度跟踪控制方法,使用模糊控制算法调节输出参量误差,提高机器腿动作稳定性,该控制方法不能有效抑制步态行进的稳态误差,在较大扰动下的控制稳定性不好；文献[5]中提出基于模糊PID变结构控制的仿生机器腿的步态稳定控制方法,采用变结构的前向三层自适应PID神经网络进行自适应学习,提高运动稳定性,该控制方法存在抗干扰性差的弱点,且对环境扰动的抑制能力不强。

针对上述问题,本文提出一种基于惯性姿态参量量化融合的机器腿仿生步态控制方法。首先对被控对象进行描述,分析控制约束条件,然后进行控制律的改进设计,最后进行了仿真测试,展示了本文方法在提高仿生机器腿步态控制稳定控制方面的优越性。

1 被控对象描述及机器腿的运动学模型构建

1.1 仿生机器腿步态控制对象描述

本文研究对象为仿人机器腿,分析机器腿行走的步态稳定控制问题。首先分析仿生机器腿的运动学模型和路径演化模型,进行控制对象和控制约束参量分析,为了简化分析,假设：1)仿生机器腿为类似于人腿的七自由度多维关节机器腿,机器腿的外形关于体坐标系x1oy1平面对称；仿生机器腿在网格区域内行走过程中,受到活动部件和关节部位的小扰动作用,其中关节力矩的扰动阻尼为一个非线性随机阻尼力,环境障碍物对机器腿步态的扰动作用表现为时滞误差,控制部件受到的阻尼力扰动是非稳态的,仿生机器腿运动链记为{A0,A1},作用力矩分布为均匀正态分布；2)忽略因仿生机器腿步进运动过程中受到的姿态变换、人为操控误差等因素的影响,惯性误差根据统计分布和经验分布量化估计[6]。根据上述假设,构造仿生机器腿步态控制的总体结构模型,如图1所示,控制模型的基础在于机器腿姿态参量的采集,采用陀螺仪和加速度计等位姿传感器等进行仿生机器腿姿态参量采集,并结合信息融合方法进行机器腿步进姿态参量的自适应处理,输出到执行器和控制器中,实现仿生机器腿的步态稳定控制。

图1 仿生机器腿步态稳定性控制的总体结构组成

根据图1,构建仿生机器腿的运动参量采集模型,机器腿的步进姿态参量采集主要有机器腿的行走速度、加速器、惯性、距离以及方位信息等,其中姿态陀螺仪采集机器腿的方位信息和惯性信息,加速度计采集机器腿的加速度和速度等参量,测距仪采集机器腿的距离和方位信息等参数,对采集的机器腿参量数据进行信息融合和传感识别,结合扩展Kalman滤波(extended Kalman filtering,EKF)进行参量估计[7],根据参量识别结果进行仿生机器腿步态稳定控制。

1.2 控制约束条件分析

进行仿生机器腿步行控制的约束条件分析,构建机器腿步进稳定控制的参量分析模型,假设τsc为传感器进行仿生机器腿姿态信息采集的时滞,τca为控制器传输到执行器的时滞。进一步建立仿生机器腿被控对象模型,给出如下约束条件：

1)仿生机器腿步行姿态校正过程中,受时滞环节的影响,在小扰动力矩作用下的步态控制模型是一个时滞二自由度模型,总的控制时延τk是确定的,满足τk=τsc+τca。

2)采用激光测距器进行仿生机器腿步进过程中与障碍物的测距,测距信息的采样周期为T；测距误差越大,对机器腿步进的方位跟踪能力越差,控制性能越差,因此,方位和距离信息是机器腿控制的重要约束参量。

3)仿生机器腿的姿态控制驱动系统为连杆系统,分布在七自由度空间内,仿生机器腿位姿发生变化时,执行器使用零阶保持器进行姿态记忆和位姿调整。

根据上述控制约束参量和约束条件,构建仿生机器腿的控制目标函数,将仿生机器腿的步态稳定性控制问题转化为一个求步态稳定控制约束参量优化和的问题。

2 控制算法改进设计

2.1 EKF

在上述构造机器腿仿生步态的运动学模型和被控对象的基础上,进行机器腿仿生步态控制算法的优化设计,本文提出一种基于惯性姿态参量量化融合的机器腿仿生步态控制方法,采用陀螺仪和加速度计等位姿传感器进行姿态参量采集,考虑由N个仿生机器腿姿态采集敏感元件组成的传感阵列进行仿生机器腿姿态参量测量,得到仿生机器腿步态测量离散线性约束参量模型描述为

x(k+1)=A(k)x(k)+Γ(k)w(k)

(1)

zi(k)=Hi(k)x(k)+ui(k),i=1,2,…,N

(2)

式中x(k)∈Rn×1为传感器陀螺仪、加速度计组成的传感器基阵的测量矩阵,A(k)∈Rn×n为相应的步态测量转移矩阵,步态控制的扰动项w(k)为均值为零且方差为Q(k)的标准正态分布随机干扰,Γ(k)为仿生机器腿三轴加速度计的测量驱动矩阵。zi(k)∈Rp×1为第i个静态角度组合矩阵,为一个实对称矩阵；Hi(k)∈Rp×n为机器腿步态姿态角估计的动态测量矩阵。

以上述采集的姿态参量为输入,进行EKF,实现机器腿的惯性姿态参量融合,扩展Kalman滤波器结构框图如图2。

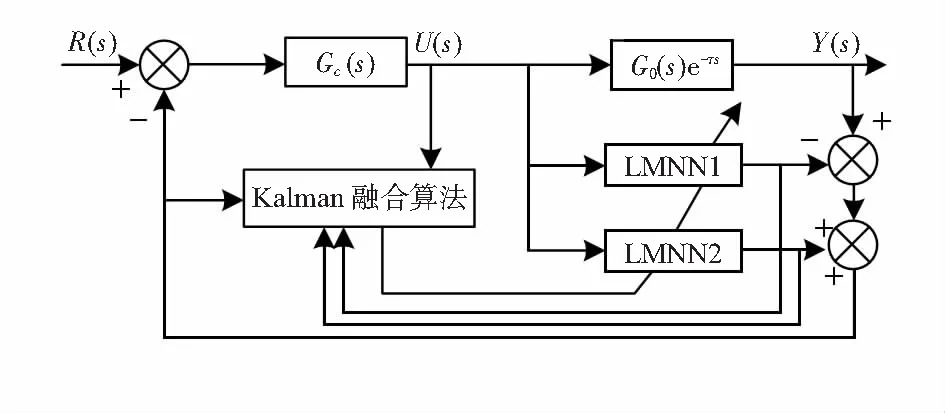
图2 扩展Kalman滤波器结构

由图2对读取的机器腿步态跟踪传感器数据进行误差补偿和迭代控制,EKF则第k次迭代的机器腿步态跟踪动态方程为

(3)

将陀螺仪角度估计作为过程数据,第k次跟踪误差为ek(t)=yd(t)-yk(t),EKF的控制律可以表示为第k+1次卡尔曼滤波输入是第k次机器腿步态参量修正输入和第k+1次控制误差的反演积分修正项的和,即

(4)

式中kp,ki为姿态角估计的动态增益矩阵。通过上述处理,采用EKF方法进行机器腿的惯性姿态参量融合和误差修正,并输入到时控制执行器中,进行机器人步态调整[8]。

2.2 姿态参量误差反馈修正及控制优化输出

针对未知扰动对机器腿步态参量控制的误差,采用自回归更新方法进行姿态参量误差反馈修正,给定一个相应的误差融合期望参考轨迹yd(t),寻找一种学习控制律的对机器腿的步进误差进行量化融合跟踪,得到伴随参考轨迹yd(t)。对于每次迭代时任意的给定的惯性姿态参量量化融合参考输入u0(t)和初始状态xk(0),采用闭环控制方法进行误差反馈控制,则在时间t内得到量化融合的状态参考序列{xk(t)}k≥0,{yk(t)}k≥0和{uk(t)}k≥0唯一收敛于xd(t),yd(t),ud(t)的充分条件为

ρ[(I+kpD(t))-1]<1,∀t∈[0,T]

(5)

式中ρ为组合姿态测量参考门限,相应必要条件是

ρ[(I+kp(t)D(t))-1]t=0<1

(6)

采用连续EKF进行姿态估计[9],得到机器腿仿生步态控制律收敛在时间区间t∈[0,T]内需满足如下条件:

1)∀t,u1,u2,x1,x2,满足‖f(t,x1,u1)-f(t,x2,u2)‖≤M(‖x1-x2‖+‖u1-u2‖),M>0；

2)∀t,x1,x2,有‖g(t,x1)-g(t,x2)‖≤M‖x1-x2‖,M>0；

3)相应的误差融合参数{δxk(0)}k≥0是收敛于0的序列；

4)有且只有一个期望的机器腿步态跟踪轨迹的输入ud(t)可以使参考模板参量达到期望值；

5)对于所有的t∈[0,T] ,多传感器信息融合矩阵(I+kpD(t))的逆存在。

根据上述稳定性收敛条件,在限定稳态误差条件下,采用自回归更新方法进行姿态参量误差反馈修正[10,11],得到机器腿仿生步态稳定控制的参量解算优化矩阵为

Φ1=[xT(k)xT(k-τk)KT]

(7)

(8)

以机器腿的步进的侧向偏移作为滤波融合的测量噪声协方差,得到机器腿步态稳定控制的姿态参量量化融合控制律等价于

Φ2=[xT(k)xT(k-τk)KTwT(k)]

(9)

(10)

当满足矩阵不等式成立时,存在

(11)

根据Lyapunove稳定性条件,得到本文设计的机器腿仿生步态控制算法是稳定收敛的。

3 仿真实验与性能分析

为了测试本文方法在实现机器腿仿真步态稳定性控制中的应用性能,进行仿真实验,实验建立在MATLAB仿真软件基础上,机器腿为自主研发的Smart II型仿人仿生机器腿,机器腿步态分为行走步态、跑步步态两种形式,分别在存在干扰障碍物和不存在干扰障碍物的情况下分析机器腿的仿生步态控制问题,机器腿所处的工作环境尺寸为一个300×300的网格区域模型,网络区域中设定了含有不规则障碍物的阵元分布流场,分析仿生机器腿在网格环境中的步态行为,机器腿的工作环境如图3所示。

图3 仿生机器腿的工作环境描述

在图3所示的仿生机器腿行走网格工作环境中,进行机器腿的步态稳定性控制分析,机器腿步进运动的初始测量状态向量为：X=[0.12 0.25 0.15 0.45]T,Kalman滤波融合的惯性参数ε1=0.1,误差修正的迭代步长为20,机器腿仿生步态行进的侧向位移偏差与真值期望值设定为0.35 rad,根据上述仿真环境和参量设定,进行机器腿仿生步态控制仿真实验,在对仿生机器腿行走步态参量的采样时间间隔设定为0.02 s的条件下,测量仿生机器腿的惯性姿态测量值,并采用本文方法和传统方法,在不同阻尼干扰强度下得到机器腿仿生步态参量的量化跟踪结果如图4。

图4 机器腿仿生步态参量的量化跟踪结果

分析图4结果得知,采用本文方法进行机器腿仿生步态,步态参量具有更好的量化跟踪和误差修正能力,提高了机器腿仿生步态控制的精度。采用本文方法和传统方法,得到机器腿步态跟踪的误差对比结果如表1,分析得知,本文方法的控制误差最小,响应能力和收敛性较好,提高了机器腿控制的稳健性。

表1 机器腿步态跟踪控制误差对比 cm

4 结 论

研究表明：本文方法能提高机器腿仿生步态控制的参量准确跟踪能力,提高机器腿步进的姿态稳定性和准确定位性。