非线性回归机器人运动参数估计方法*
郑 杰, 张 华, 肖宇峰
(西南科技大学 信息工程学院,四川 绵阳 621000)
0 引 言
机器人运动参数估计是机器人研究中尤为关键的问题,对于机器人的导航、定位、路径规划以及目标跟踪等具有十分重要的意义。为解决此问题,研究人员提出了多种方案:文献[1~6]的方法均存在累积误差,因而不适用于全局运动参数估计。文献[7,8]基于信标的方法虽然适用于全局位姿估计,但该方法要求在环境中放置信标,运用场景受到限制,尤其在室外环境。目前,较为可行的方案是通过安装激光雷达估计机器人[9,10]的运动参数方法精度高,且不需要对环境做任何改动,而成为该领域的研究热点。文献[11]提出角度直方图(angle histogram)算法将三维搜索问题转换成3个一维搜索问题,大大降低了计算量,但算法要求环境具有明显的线段特征,且精度受到直方图分辨率的影响。文献[12]提出的迭代最近点(iterative closest point,ICP)算法精度和鲁棒性均高于基于特征的对应方法。但激光测量数据多,导致ICP算法的计算量大,收敛速度慢。此外,ICP算法与其他基于对应的方法一样具有局部最小值问题。文献[13]在ICP算法的基础上,提出了IDC(iterative dual correspondence)算法。其优势在于能够处理任意角度的旋转且收敛速度比ICP快。但在实际应用中,IDC算法的计算量仍然比较大[10]。
本文提出一种非线性回归的机器人运动参数估计方法,通过实验验证本文算法能够实时准确地对机器人运动参数进行估计,并与ICP算法进行了比较。
1 运动模型分析
系统坐标系建立如图1所示,假设OX0Y0为世界坐标系,OXY为机器人坐标系,OXLYL为激光雷达坐标系。本文机器人采用两轮驱动模型,形式图1。

(1)


(2)

(3)
结合线速度矢量在相关坐标系统上的投影,可将式(3)表示为
(4)
2 运动参数估计模型转换

将上述微分公式的差分项dx和dy代入相对运动方程(3)中[14],得到公式
(5)
3 运动参数估计

Aiω+Biv+Di=0
(6)

但在实际测量过程中,由于激光雷达所反馈的数据含有噪声,并且该噪声的特性的计算非常困难,因此,在这里假设测量结果中出现的噪声为符合高斯分布的随机噪声序列ξ,则测量公式表示为
(7)

zi=HiXi+di+ξi
(8)
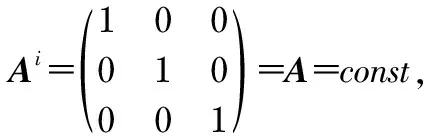
(9)
其中,卡尔曼增益为Ki=ATPiHT(HPiHT+R)-1。进而进行进一步的误差估计。
4 特殊情况分析
1)机器人沿着平坦的墙壁移动

2)机器人在圆形地形中旋转
让机器人围绕自身坐标系的原点旋转,而机器人四周的环境是一个圆柱体,其轴线垂直于OXY平面,并穿过机器人坐标系原点。
在这种情况下,运动方程(4)具有形式f(x,y,t)=x2+y2-R2=0,经过计算,可以得到关于ω,v公式:0·ω+2yv=0。与前一种情况相似,将得到方程的解为v=0,ω是任何实数。因此,这种情况下无法确定角速度。
3)机器人向平坦的墙壁上移动

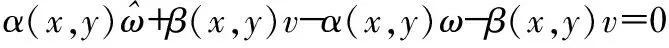
(10)

5 实验结果与分析
在实验室走廊搭建实验环境。以TurtleBot2为实验平台(如图2(a)所示)搭载Hokuyo URG—04LX激光雷达,获得实验环境的激光雷达数据并进行建模。实验中,机器人的移动环境是一个封闭的矩形空间,如图2(b)显示了RVIZ中激光雷达的一帧图像。

图2 实验平台实物图及激光雷达数据
机器人的运动由平移和旋转组成,根据上述的运动参数估计方法,对获得的激光雷达数据进行处理,最终得到机器人的运动参数。图3为上述方法估计的线速度和角速度。

图3 运动参数估计值
图3表明:线速度和角速度的估计值快速收敛,但在函数f(x,y)的拐点处获得的数据具有不连续性,这是由于在拐点处函数偏导数不存在所致。通过对激光雷达的扫描点设置阈值,以去除这些点的影响,可以极大程度地提高估计的收敛速度及准确度。
图4中将运动参数估计方法所估计的值与运动固有参数进行对比。从图中可看出,相比于原始数据,所提出方法的估计值具有较高的收敛精度,且收敛时间短。
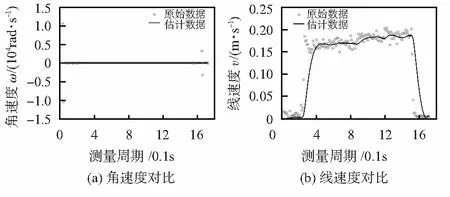
图4 参数对比
图5是在不同运动情况下,通过本文算法估计后的机器人运动位置坐标与ICP算法结果的对比。从图中可以看到:该算法与ICP算法具有相似的精度。

图5 机器人运动的坐标
通过将机器人运动位姿情况与地形数据整合,得到实际机器人运动轨迹如图6所示。从图中可以看出:在不同的地形环境以及不同的运动情况下,该算法都能够平滑地估计出机器人的运动参数。

图6 获得的机器人的地形和运动轨迹
6 结束语
本文通过建立与分析线速度和角速度估计的数学模型,转换参数估计求解模型,并利用递推最小二乘的方法与卡尔曼滤波来求解参数与消除误差。本文方法精度高、运算速率快。延迟时间为对一个点多次扫描的积累所花费的时间,但由于现代测距仪允许获得高频(例如75 Hz)的扫描,与获得几次扫描相关的延迟将是可忽略的,因此,能够实时估计机器人运动参数。最后将本文方法在实际的机器人系统中进行实验验证,结果验证了所提出方法的有效性。

