平均风速对海上风力机塔架动力响应的影响

张建平, 龚 振, 张智伟

(1.上海电力学院, 上海 200090; 2.上海绿色环保能源有限公司, 上海 200433)

目前,随着风力机容量的不断增大,塔架在风载荷作用下的可靠性愈加受到国内外学者们的关注。刘雄等人[1]分析了塔架的气动阻尼和结构阻尼,并将塔架简化成悬臂结构,得到了其在变载荷作用下的动态响应。闫海津等人[2]考虑塔架效应,利用FLUENT软件研究了风力机塔架附近的流场。张湘伟和文武[3]研究了大型风力机塔架在脉动风下的动力响应特性。刘新喜等人[4]基于ABAQUS有限元软件,建立了4种不同塔架形式的风力机一体化模型,探讨了不同塔架形式风力机的抗台风性能。王介龙等人[5]研究了风机不同部件之间的耦合问题,建立了桨叶、机舱、塔架的动力学方程,并利用子空间迭代方法计算了结构的动力响应。ZHANG J P等人[6-7]在考虑流固耦合作用的情况下,讨论了不同来流风速及湍流效应对风力机叶片动力响应的影响。

本文针对海上风力机建立了塔架结构的三维实体模型,基于ANSYS开展了数值模拟,分析了不同平均风速作用下考虑几何非线性的塔架动力响应,以期为优化风机结构提供参考。

1 基本理论

1.1 风载荷公式

从实际的工程计算来看,一般通过风压来表示风对结构的作用。由伯努利方程可知,风速在单位面积上的风压Fe(t)为

(1)

式中:ρ——空气密度;

v——平均风速。

由式(1)可得到风载荷计算公式[8]为

(2)

式中:CP——风压分布系数;

A——作用面积。

1.2 塔架结构控制方程

几何非线性是指放弃小位移假设,从几何上严格分析单元体的尺寸和形状变化,得到非线性的几何运动方程,由此引起基本控制方程的非线性问题。对于结构的几何非线性分析,可以归结为节点位移的非线性方程。在有限元分析中,根据系统的几何非线性特性对系统的平衡方程进行不断的修正,在新的一步增量求解前,对坐标系进行修正,然后去求解方程,并计算几何非线性对刚度矩阵和载荷阵的修正。有限元方法主要在单元体离散化的基础上实现微分方程的求解。一般情况下,塔架结构所满足的几何非线性离散运动微分方程为

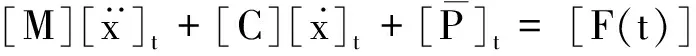
(3)

式中:[M],[C]——质量矩阵和阻尼矩阵;

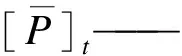
[F(t)]——塔架受到的风载荷列向量。

此外,在计算时不考虑阻尼,即阻尼矩阵[C]=[0]。

利用Newmark法,推导结构在风载荷作用下的几何非线性动力增量平衡方程。在有限元分析中,结构控制方程对应于某一时刻t+Δt的平衡方程,可表示为

(4)

式中:Δt——时间步长。

式(4)的几何非线性项可线性表示为

(5)

式中:[KT]t——t时刻的节点位移算出的切向刚度矩阵;

[x]t——结构位移,[x]=[u,vw]T。

将式(5)代入式(4),可得到

(6)

令

[x]t+Δt-[x]t=Δ[x]

(7)

通过结构的初始位移、速度和加速度计算出位移增量Δ[x],利用Newton-Raphson迭代法进行迭代计算来解决由线性化带来的误差,最终计算出结构新的位移、速度和加速度,即可得到结构整个动力响应的时程。

2 实体建模和网格划分

2.1 实体建模及参数设置

根据文献[9],用于数值模拟的海上风力机塔架几何参数如表1所示。

表1 风力机塔架几何参数 m

海上风力机塔架材料通常使用的是Q345钢材。本文中计算模拟的塔架材料Q345钢的基本材料参数如表2所示。

根据表1和表2给出的塔架参数,采用SolidWorks软件进行三维建模,并将建立的塔架实体模型导入到ANSYS中,所得模型如图1所示。

表2 风力机塔架基本材料参数

图1 风力机塔架实体模型

2.2 网格划分及网格无关性验证

塔架实体模型建立后,划分网格成为一个重要问题。依次增大网格密度,结果发现,塔架顶端最大位移随着网格单元数的增加是收敛的,如表3所示。

表3 网格无关性验证

为了保证计算精度,同时节约计算时间,这里采用23 265个网格单元数进行数值计算分析,网格划分后的模型如图2所示。

图2 塔架模型网格划分示意

3 数值结果与讨论

基于动力学分析方法,结合ANSYS Workbench软件对风力机塔架进行振动特性分析,选定8 m/s,12 m/s,16 m/s 3种平均风速(这里的平均风速指的是风的大小和方向都不随时间变化),由此开展塔架动态特性分析,得出塔架的位移和Mises应力的动态特性。

3.1 平均风速下的位移响应

图3为3种平均风速工况下,塔架顶部在风载荷作用方向上的最大位移响应曲线。

由图3可知,其中,8 m/s工况下塔架的最大位移为1.51×10-3m,12 m/s,16 m/s工况下的最大位移分别为3.39×10-3m和4.62×10-3m,这表明随着平均风速的增加,风力机塔架的位移也随之增大。

图3 塔架在不同平均风速下的位移响应曲线

图4给出了塔架最大位移随平均风速变化的曲线。考虑风速范围为8～45 m/s,由图4可以看出,最大位移随着平均风速的增大而增大,呈非线性递增关系。

图4 塔架最大位移随平均风速的变化曲线

3.2 平均风速下的应力响应

图5至图7分别为3种平均风速工况下整个风力机塔架最大Mises应力时间响应曲线。

图5 风速为8 m/s时塔架的最大Mises应力响应曲线

图6 风速为12 m/s时塔架的最大Mises应力响应曲线

3种工况下,塔架承受的最大Mises应力由8 m/s工况下的0.74 MPa增加到12 m/s工况下的1.65 MPa,16 m/s工况下的最大Mises应力是8 m/s工况下的3.04倍,表明随着风速的增加,塔架最大Mises应力也随之而增加。

与图4工况相同,给出了近海风力机塔架平均风速作用下最大Mises应力与平均风速的关系,如图8所示。由图8可以看出,最大Mises应力随着平均风速的增大而增大,基本呈非线性递增关系。

图7 风速为16 m/s时的最大Mises应力响应曲线

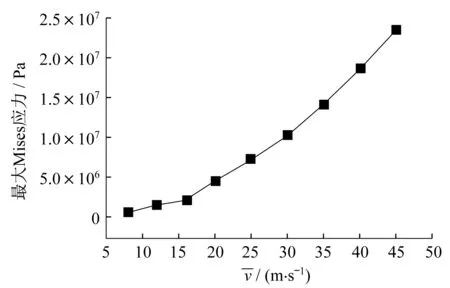
图8 塔架最大Mises应力随平均风速的变化

4 结 论

(1) 针对海上风力机塔架,建立了考虑几何非线性的离散运动微分方程,并基于Newmark和Newton-Raphson法,实现了对平均风速作用下塔架位移和Mises应力响应的求解。

(2) 从3种不同平均风速下风力机塔架的位移、Mises应力响应曲线可以发现,塔架最大位移随平均风速的增加而增加,最大Mises应力也是如此。

(3) 考虑风速范围为8～45 m/s,通过分析塔架最大位移、Mises应力随平均风速变化的曲线可以看出,塔架最大位移和Mises应力均随平均风速的增大而增大,且呈非线性递增关系。