串联型粘弹-粘塑性沥青混合料本构模型的有限元分析
徐建平, 朱耀庭
(1. 重庆交通大学 土木工程学院,重庆 400074; 2. 江西省高速公路投资集团有限责任公司,江西 南昌 330025;3. 江西省交通科学研究院,江西 南昌 330038)
0 引 言
沥青混合料的力学性能研究在道路工程中处于基础性地位,对全面掌握沥青路面结构行为具有重要作用。沥青混合料是典型的粘、弹、塑性综合体,其力学行为与加载速率、荷载时间以及温度等因素密切相关[1]。
为能对沥青路面结构进行更精确地应力应变分析,有必要对串联型粘弹-粘塑性本构模型进行有限元实现。目前学界对沥青混合料与时间的相关模型进行了研究与探讨[2-7],将与时间率相关模型植入有限元分析程序中,实现了沥青路面结构有限元计算与分析。然而,对于沥青混合料多阶段串联型粘弹-粘塑性本构模型的有限元实现还少见报道。
笔者针对目前沥青混合料串联型粘弹-粘塑性本构模型有限元实现方面的不足,在分析串联型模型力学特性的基础上,分别对粘弹、粘塑本构模型的增量离散化,采用数值稳定的径向回退与向后欧拉积分方法[8-9],并结合连续迭代R-M理论[10],将编写的材料本构模型子程序移植至有限元软件ABAQUS中,从而实现了对沥青混合料粘弹-粘塑性力学行为的数值模拟和分析。笔者通过建立隐式应力积分方程,并推导迭代所需的一致切线刚度矩阵,最后利用算例验证了有限元实现的有效性。
1 粘弹性本构方程有限元
针对沥青混合料的粘弹塑性力学特性,笔者在热力学理论基础上建立了串联型粘弹-粘塑性本构模型,一维模型如图1,本构方程如式(1)。利用室内试验方法和数学计算对本构模型进行了参数获取和敏感性评价[11]。

图1 串联型粘弹-粘塑性本构模型Fig. 1 Serial viscoelastic-viscoplastic constitutive model
(1)
式中:pr、lr、h、m、c、γ、q、b、β、s分别为粘弹-粘塑性材料常数。
根据Boltzmann线性叠加理论,可通过一个遗传积分方程将各向同性粘弹性材料应力应变关系表示如式(2)[12]。
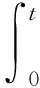
(2)
式中:σij(t)为应力张量;Sij(t)为偏应力张量;σkk(t)/3为应力张量第一不变量;Gijkl(t)为剪切松弛张量;Kijkl(t)为体积松弛张量;ekl为偏应变张量;εv为体积应变;上标符号表示为对时间的一次求导。
假定tr时刻应力状态已知,将荷载作用时间划为离散时间间隔为tr+1=tr+Δt,通过Prony级数性质表示广义Maxwell模型力学特性,以此推导出遗传积分应力增量在Prony级数条件下的表现形式如式(3)。
(3)
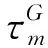
式(3)包含了弹性及粘性部分偏应力。对粘性部分积分进行单独分析时,每个子模型粘性应变化可以通过式(4)来表示。
(4)
在时间增量为Δt条件下,式(4)变化可表示为式(5):
(5)
由式(4)、(5)可得式(6):
(6)
假定在时刻tr≤t≤tr+Δt内,粘弹性行为服从等应变率为Rε变化,如式(7):
(7)
式(7)等号两边各减去tr时刻粘性应变,可得到粘性应变增量如式(8):
(8)
则有式(9):
(9)
同理可推导出体积应力增量,其表达式如式(10):
(10)
上述递推关系式可转化为式(11):
(11)
定义偏应力对偏应变的变化率为剪切切线模量GT,体积应力对体积应变的变化率为体积切线模量KT,法向应力增量可通过应力的体积增量和偏增量进行表示,得出GT和KT表达式如式(12):
(12)
在有限元计算中,还需推导一致切线刚度矩阵,根据Jacobian矩阵的定义[13]可得出如式(13):
(13)
2 粘塑性本构方程有限元
由于粘塑性本构模型方程是用时间导数微分方程表示,如何利用精确和有效的数学算法对模型方程进行积分运算,是有限元实现过程中遇到的最大困难。有限元计算采用等参单元,对本构模型方程积分过程是通过高斯点计算来实现,而更新的材料参数为应力和粘塑性两个变量。所采用数值算法必须满足以下4个基本条件[14]:① 被积分后的表达方程与粘塑性本构方程相一致;② 数值方法是稳定的;③ 粘塑性增量是一致的;④ 具备二阶精确度。因此,隐式积分算法可保证应力结果准确性,能满足上述基本条件,笔者将在向后欧拉积分算法基础上,建立粘塑性本构方程的一致切线算子。
2.1 本构方程的离散化和返回映射
粘塑性本构模型采用一组微分方程和其初值条件进行表述,微分方程组由应变增量通过积分离散计算进行实现,由于向后欧拉方法具有数值有效性和绝对收敛性,因而被广泛应用于(粘)塑性有限元数值计算中[15-16]。采用后退欧拉积分的方法将粘塑性本构方程离散,并对硬化方程进行表述,方程离散后表示如式(14):
(14)
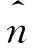

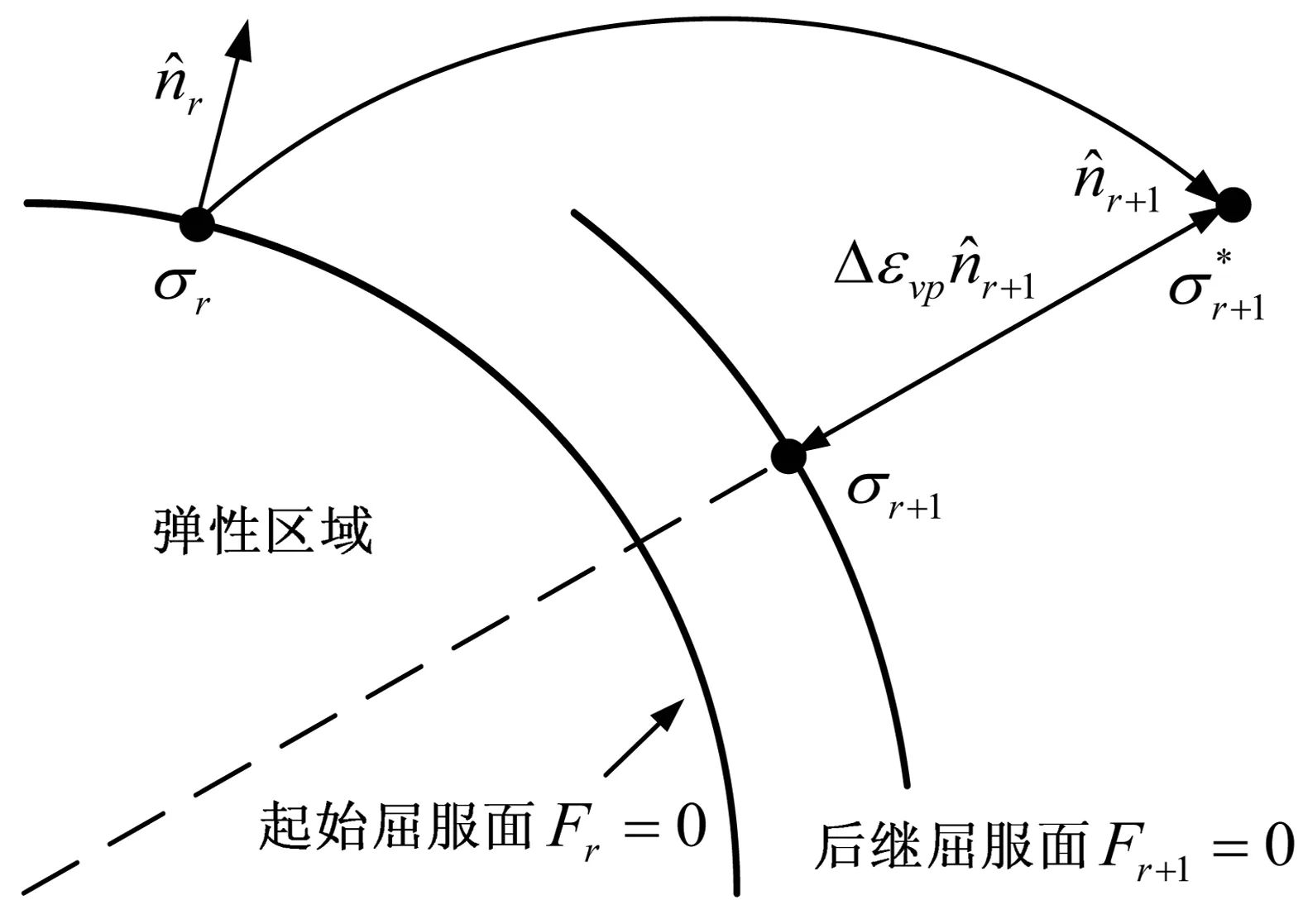
图2 径向回退法几何阐述Fig. 2 Geometrical view of the radial regression method
若tr时刻σij(tr)、εij(tr)、εvpij(tr)、Xij(tr)等力学状态变量均为已知,通过给定Δεij(tr+1)和Δt,则可采用弹性预估-塑性校正方法求出tr+1时刻的各个变量。假设给定的应变增量Δεij(tr+1)全部为弹性应变,则引入弹性尝试应力如式(15):
(15)
式中:Cijkl为弹性模量4阶张量。
此时,屈服准则由弹性尝试应力改为式(16):
(16)
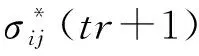
(17)
式中:CijklΔεvpkl(tr+1)称为粘塑性校正项。
由此可见,只需求得εvpkl(tr+1),则σij(tr+1)等变量将容易获得。
假定粘塑性材料各向同性,且塑性不可压缩,则粘塑性校正项偏量可通过材料剪切模型进行表示,如式(18):
(18)
则由式(18)可得式(19):
(19)
则得出有效应力第2不变量如式(20):
R[ΔP(tr+1)]
(20)
式(20)可表示为累计粘塑性应变ΔP(tr+1)的方程,对有效应力第2不变量进行表示如式(21):
(21)
式(20)和式(21)得到一个关于ΔP(tr+1)的非线性方程,如式(22):
(22)
当ΔP(tr+1)求解得出后,则可求解出时间子步条件下各变量增量,从而得出各变量。值得指出的是,式(22)为一非线性方程组,可采用N-R迭代方法对未知变量进行求解,计算流程如图3。
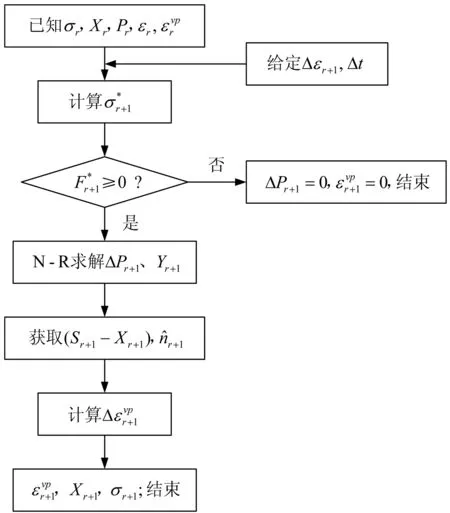
图3 N-R迭代算法流程Fig. 3 N-R iterative algorithmic process
2.2 一致切线算子
有限元程序在计算积分过程中,在时间增量结束时,一致切线刚度矩阵d△σij/d△εij用于表示应变增量的无穷小变化情况下的应力分量变化。对式(14)进行微分推导,可得Jacobican行列式如式(23):
(23)
3 串联型粘弹-粘塑性模型有限元
串联型粘弹-粘塑性本构模型有限元计算与弹塑性材料相类似,计算之初需要判断材料是否已经进入屈服阶段,在未进入屈服之前只表现为粘弹性行为,而进入屈服阶段以后则表现为粘弹性和粘塑性的共同响应,应变则表现为粘弹性与粘塑性应变之和。因此,串联型粘弹-粘塑性模型的有限元计算本质上和粘弹性或粘塑性分析本质上时相同的,需根据屈服法则对各个有限元单元做出屈服判断,然后按不同应力应变状态做出相应的判定和计算处理。对于已进入屈服的有限元单元采用粘塑性计算方法,对未进入屈服的有限元单元则采用粘弹性方法进行分析。其有限元计算流程如图4。

图4 串联型粘弹-粘塑性有限元计算流程Fig. 4 The calculation process of serial viscoelastic-viscoplastic finite element model
4 数值验证
笔者利用ABAQUS有限元平台进行有限元用户材料(UMAT)子程序的二次开发和编程[18]。通过对室内实验进行模拟,计算结果与实验数据对比,以验证数值实现的准确性。由于文中所涉及本构模型为串联型,要准确获取材料模型参数要将粘弹性和粘塑性进行解耦和分离,对材料行为时间相关性进行分配,基于此提出的策略为:通过小应力幅值动态试验获取粘弹性材料参数,利用静态蠕变试验对粘弹性和粘塑性解耦获取粘塑性力学行为,结合本构模型特征编制数据拟合程序,得出粘塑性模型参数,具体模型参数和实验数据请见文献[2]。
沥青混合料动态模量和静态蠕变室内试验采用的是圆柱形试件,试件高度为150 mm,直径为100 mm。试件几何尺寸、荷载和边界条件均轴对称,可采用轴对称单元模型以简化为二维模型进行计算,但笔者编制的UMAT子程序仍考虑到了三维状态条件。
建模中,有限元模型尺寸和试件相同,刚体模拟加载压头和支撑底座。有限元模型网格划分通过剖分和扫掠方法得到圆心向圆周发散的三维网格,单元类型为20结点减缩积分单元C3D20R。在实际的试验过程中,对试件底面并没有进行约束,同时由于实验过程采用双层乳胶膜以保障试件端面的自由变形,只进行了Z方向约束,即U3=0。试件顶面为在施加均布应力的加载方式。
4.1 粘弹性结果
粘弹性材料响应的表征可体现为蠕变和应力松弛,由于沥青混合料材料的特殊性,一般室内对粘弹性采用蠕变实验获取蠕变应变或柔度,再通过蠕变和松弛之间的粘弹性关系,可计算出松弛应力或模量[19]。计算结果如图5。
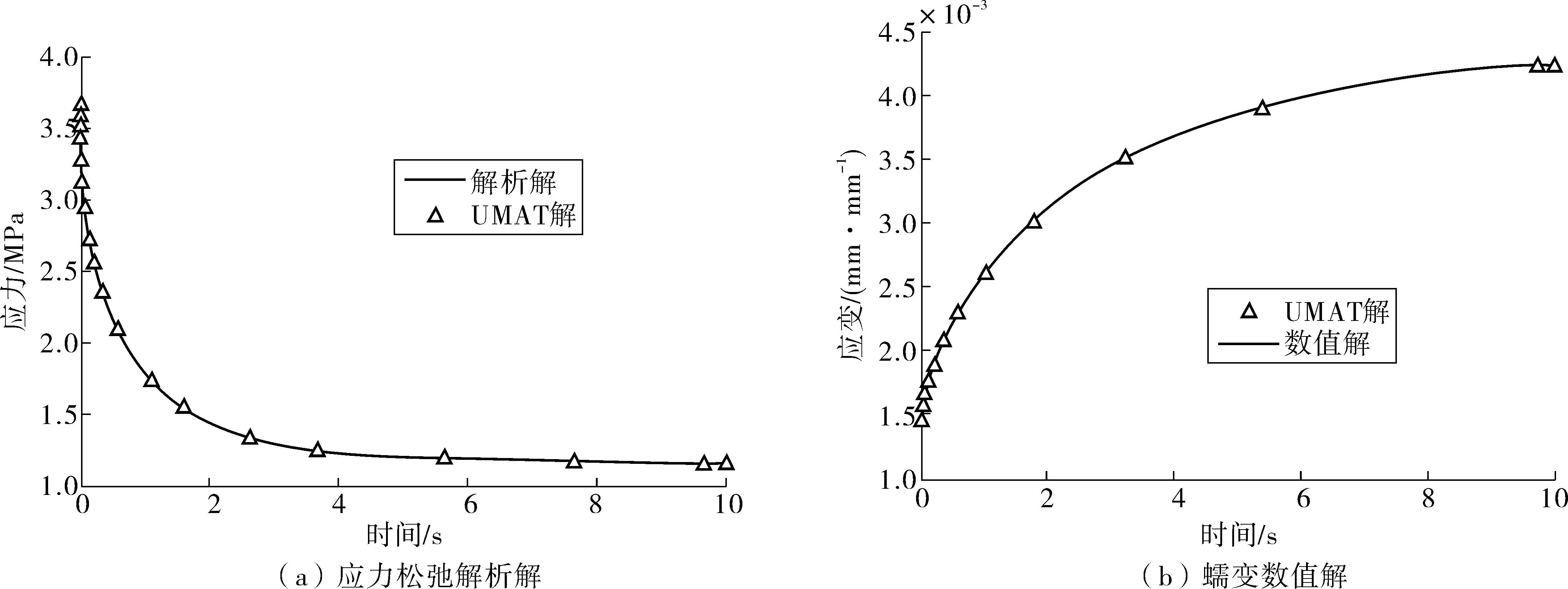
图5 应力松弛解析解和蠕变数值解与UMAT计算对比Fig. 5 Comparison between analytical solution of stress relaxation and numerical solution of creep and UMAT calculation
由松弛和蠕变计算结果可看出:粘弹性UMAT应力松弛计算解和解析解基本上相同,结果几乎无差别,而蠕变有限元解和数值解也基本上相同,表明有限元子程序有非常好的准确性。
4.2 粘塑性结果
粘塑性本构方程由一组隐形方程组构成,无法直接得出解析解,通过文献[2]中改进的有限差分格式可获取本构方程的数值曲线,本节采用蠕变模拟进行差分解和有限元解的对比分析。同时,由于粘塑性需要采用达到屈服条件才可验证,模拟加载应力需大于材料的粘塑性屈服应力。不同条件蠕变计算结果如图6。
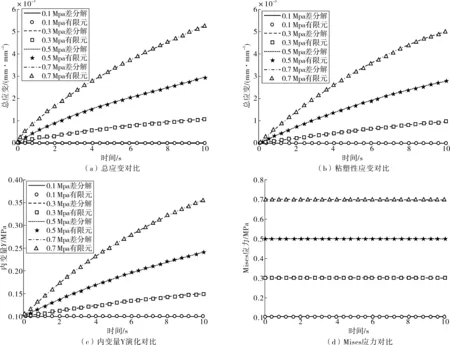
图6 有限元计算和改进差分法计算结果对比Fig. 6 Comparison between the calculation results of finite element calculation and the improved difference method
由蠕变实验模拟和计算结果对比可知,粘塑性子程序是准确和可靠的,能正确地反映出粘塑性材料的力学响应和内变量的发展趋势。
4.3 串联型粘弹-粘塑性结果
串联型粘弹-粘塑性材料的有限元计算之初要判定材料是否已进入屈服阶段,在未进入屈服以前只表现为粘弹性行为,进入屈服以后则表现为粘弹性及粘塑性共同响应。因此,串联型粘弹-粘塑性计算结果验证分为两个阶段,一个为材料未达到屈服状态;另一个为材料进入屈服状态而发生了粘塑性变形。未进入屈服和进入屈服状态的模拟结果如图7、8。
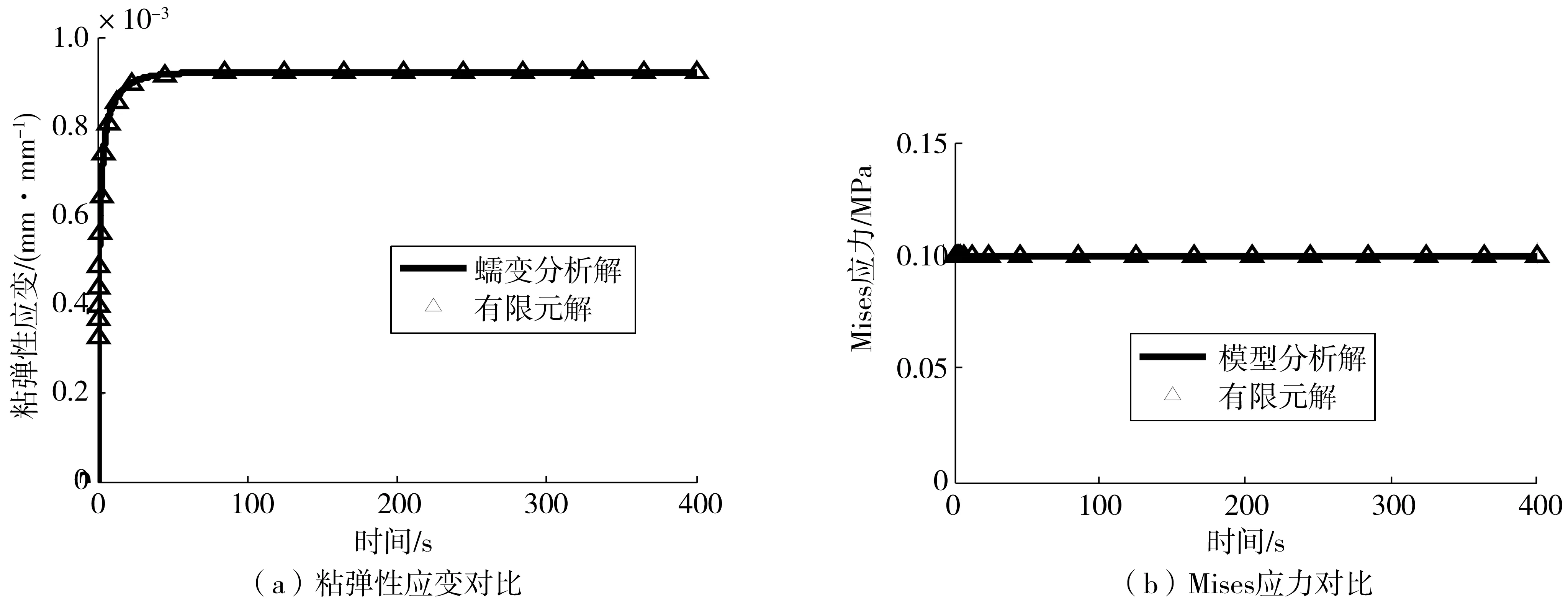
图7 未达屈服条件下计算结果对比Fig. 7 Comparison of calculation results under non-yield conditions

图8 屈服条件下计算结果对比Fig. 8 Comparison of calculation results under yield condition
由图7、8可见:无论屈服状态还是未达屈服状态,计算结果和理论分析都具有很好一致性,串联型粘弹-粘塑性本构模型有限元实现是有效的,能准确反映出沥青混合料与时间相关力学行为发展和演化规律。
5 结 论
笔者以沥青混合料与时间相关本构模型为研究对象,通过编制用户子程序,对串联型粘弹-粘塑性模型进行了有限元分析,通过沥青混合料试件在典型室内试验条件力学行为进行了有限元模拟和室内试验数据的对比,验证了笔者提出方法的正确性和可靠性,并得出以下结论:
1)串联型本构模型的有限元可依据模型特点表示为粘弹性和粘塑性两部分的应力相同而应变相加;
2)通过递推关系得出粘弹性、粘塑性本构模型的离散化方程,数值解和解析解进行对比,其结果基本一致,验证了文中模型离散化法有效性;
3)粘塑性模型采用径向回退与向后欧拉积分方法,并结合连续迭代R-M法可有效地解决模型离散化非线性方程组计算过程的稳定性和收敛问题;
4)当将串联型模型用于沥青路面结构计算中,只需将沥青结构层材料定义为模型属性即可快速实现路面结构永久变形计算和分析。

