基于改进层次分析法的煤矿应急管理体系评价

吴林林

（山西焦煤霍州煤电汾河焦煤公司三交河煤矿，山西 霍州 031400）

0 引言

矿井应急管理体系的建立和完善是保障矿井生产安全、降低事故发生风险和降低灾难损失的基础[1]。对应急管理体系脆弱性的平均，涉及到人员、物资、环境以及管理等多方面的因素，合理确定各因素所占权重，有助于发现管理体系中的薄弱环节，提出相应的改善措施有着重要的意义。对于权重的确定方法，常用的有最大权原则、二项系数法、层次分析法和最小平方法等[2-3]，各方法具有其优劣，结合实际条件，考虑到矿井应急管理体系具有层次性的特点，本文以层次分析法为基础，结合群决策和灰色理论，对层次分析法进行改进，有效避免了层次分析法的主观性和偶然性，为煤矿建立合理的应急管理体系提供理论依据。

1 影响因素分析

根据矿井生产实际，认为影响煤矿应急管理体系的主要有4个一级因素和17个二级因素，根据层次分析结构，建立评价指标体系图，如图1所示。

1）人的脆弱性：矿井生产管理人员是影响应急管理的主要因素，工作人员的生理和心理状况、安全意识、技术能力以及应急素质都对矿井应急管理有着一定影响，生理和心理状况越差、安全意识越淡薄、技术能力越低、应急素质越不好，矿井应急管理体系也就越脆弱；

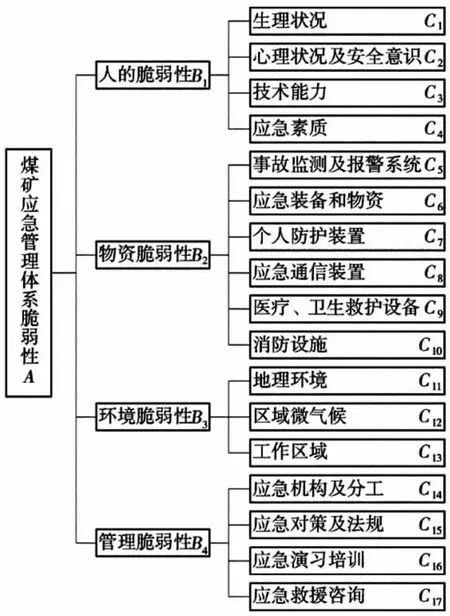
图1 煤矿应急管理脆弱性评价体系图

2）物资脆弱性：影响煤矿应急管理体系的主要物资包括矿井监测和报警系统、应急装备物资、个人防护装置、救护设备以及消费设施5个，相关物资设备越不完善，管理维护越差，应急管理体系也就越脆弱；

3）环境脆弱性：矿井所处环境对应急管理体系也有一定影响，主要包括地理环境、区域微气候以及工作区域3项；

（4）管理脆弱性：科学有效的管理措施是影响矿井应急管理的重要因素。制定合理的管理体系，能够有效保障矿井生产安全，最大程度的降低事故发生后的损失。主要包括应急机构及分工、应急对策及法规、应急演习培训和应急救援咨询4项。

2 应急管理体系脆弱性评价

2.1 构建判断矩阵

根据上述分析，确定影响煤矿应急管理体系脆弱性的主要因素，下面利用层次分析法、群决策和灰色理论构建评价矩阵，对应急管理体系的脆弱性进行评价。

假设共有m位专家，利用1-9标度法，对各影响因素两两比较，建立判断矩阵，与常规层次分析法不同，此处并不给出具体的标度值，只是给出一个标度区间灰数，得到每位专家的灰数判断矩阵如式（1）所示。

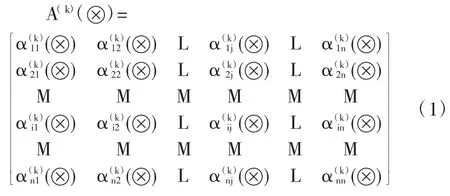
式中，A（k）（⊗）为应急管理体系脆弱性评价矩阵；(⊗)为第k为专家对第i，j个指标比较后给出的灰数值，（k=1,2，…，m），（i=1,2，…，n），（j=1,2，…，n）；n为同级指标的个数。根据相关理论，有(⊗)=1，(⊗)·(⊗)=1，(⊗)∈（(⊗)(⊗)）(⊗)(⊗)分别为灰数的下限和上限。

根据式（1），构建各级指标的群体灰数判断矩阵，如式（2）所示。

式中：A（⊗）为应急管理体系群体灰数判断矩阵；αij(⊗)为m位专家对第i，j个指标比较后的综合灰数值，且有 αij(⊗)分别为下限和上限。

根据加权几何均值算法，下限和上限可以表示为：

式中：wk为第k位专家占m为专家总体判断的权重。

对上述灰数判断矩阵进行白化，可得白化矩阵如式（5）所示。

式中：A%（⊗）为白化矩阵；α%ij(⊗)为第 i，j个指标相比较所得灰数的白化值；ρij为灰数判断矩阵的定位系数，且有 ρij∈[0,1]，ρij=1-ρji，（i=1,2，…，n）（j=1,2，…，n）。

2.2 白化矩阵一致性检验

为了检验上述白化矩阵的可靠性，对其进行一致性检验，其检验公式如式（7）、（8）所示。

式中：CI为矩阵的一致性检验指数；λmax为矩阵的最大特征值；N为矩阵的阶数；CR为一致性比率；RI为随机一致性指标，其取值见表1。

表1 随机一致性指标RI取值

当式（8）所得一致性比率CR＜0.1时，则所得白化矩阵较为可靠，评价结果是相对准确的，否则，则需要对白化矩阵进行调整，直至一致性比率CR＜0.1。

2.3 应急管理体系脆弱性评价

计算得到白化矩阵的最大特征值λmax后，根据其对应的特征向量W，进行归一化处理，所得数值即为该指标所占上层指标的权重。利用该方法对各影响指标逐个逐层进行计算，得到各指标所占权重，将下层指标权重与对应的上层指标权重相乘，得到各二级因素占应急管理体系的综合权重，其中，所占权重最大的因素就是导致应急管理体系脆弱的主要原因，即为应急管理体系中的最薄弱环节，应相应提出改善措施，保障矿井的安全生产。

3 实例分析

为了检验上述评价模型的准确性，根据温庄煤业实际生产条件，选取3位专家参与评判，对矿井应急管理体系进行综合评价。3位专家编号依次设为 M1、M2和 M3，对一级影响因素 B1～B4的灰数判断矩阵如表2～表4所示。

表2 专家M1的灰数判断矩阵

表3 专家M2的灰数判断矩阵

表4 专家M3的灰数判断矩阵

利用上表的计算结果建立群体灰数判断矩阵，设定3为专家判断的权重相同，均为1/3，根据式（3）、（4），得到群体灰数判断矩阵。取 ρij=ρji=0.5，利用式（5），对矩阵进行白化，所得结果如表4所示。

表5 群体白化判断矩阵

计算表5所示白化矩阵的最大特征值为λmax=4.0608，矩阵所对应的特征向量为

根据表1，可知对于4阶矩阵的随机一致性指标 RI为 0.90，将数据代入式（7）、（8），可得白化矩阵的CI=0.0228，小于0.1，满足相关要求，所得结果较为可靠。

根据上述方法，分别计算各二级影响因素C1～C17所对应的一级影响因素 B1～B4的白化矩阵，然后分别进行一致性检验，各因素的一致性比率均小于0.1，满足相关要求。

根据前面计算所得的白化矩阵最大特征值对应的特征向量W，进行归一化处理，计算各因素所占权重，即各因素的脆弱性值。根据计算结果，归一化向量W1为：

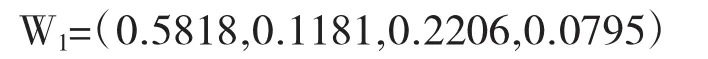
即各二级因素 B1～B4的脆弱性质分别为0.5818、0.1181、0.2206、0.0795。

根据同样的方法，可得C1～C4相对B1的脆弱性值依次为 0.0812、0.2283、0.5378、0.1527，将以上结果与B1的脆弱性质0.5818相乘，可得C1～C4相对于指标A的脆弱性值依次为 0.0472、0.1328、0.3129、0.0888。然后分别计算C5～C17相对指标A的脆弱性值，所得结果如表6所示。

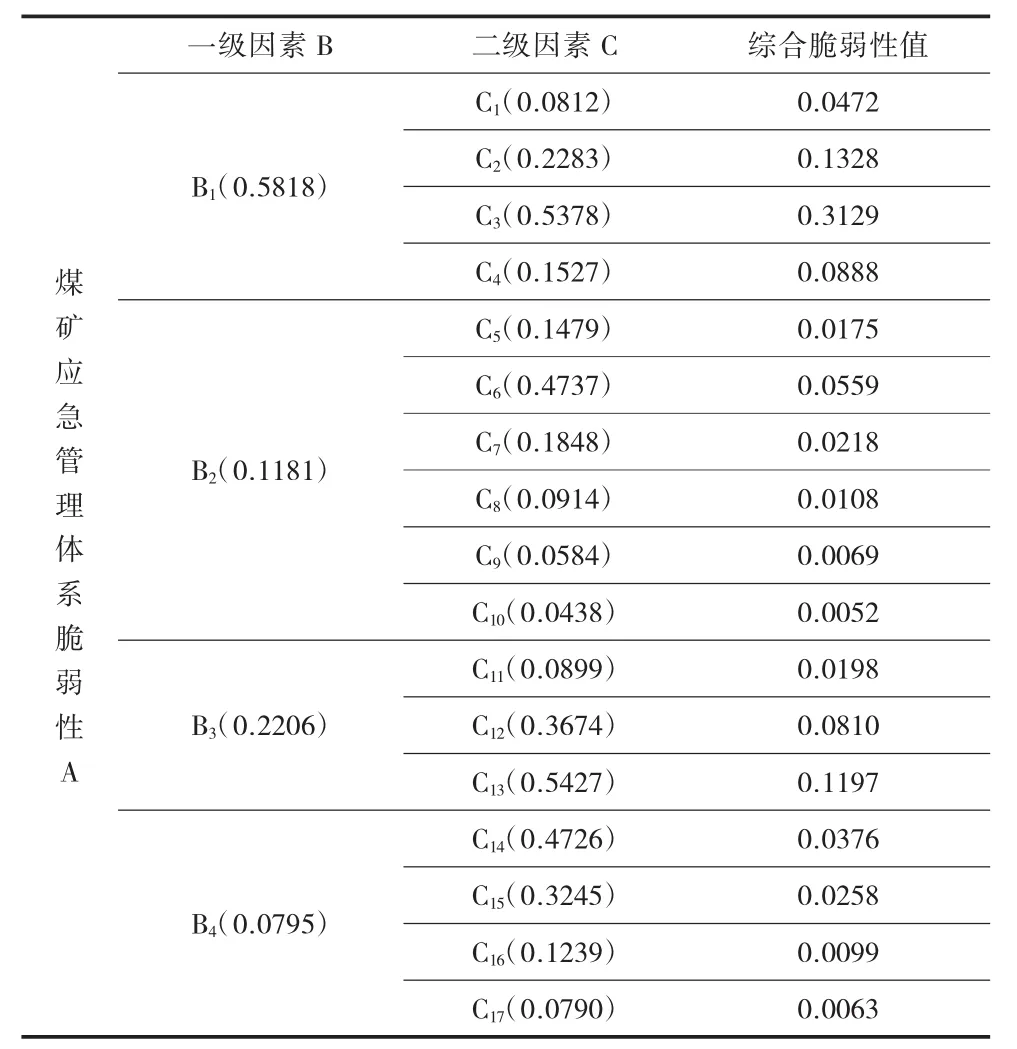
表6 综合脆弱性值计算结果

根据表6所得结果，对综合脆弱性质从大到小依次排列，脆弱性质最大的为人员技术能力C3，脆弱性值为0.3129，其次为心理状况及安全意识C2，脆弱性值为0.1328，第三为环境条件中的工作区域C13，脆弱性值为0.1197。这三项是影响温庄煤业应急管理体系的最薄弱环节，应有针对性的进行补强改进，以保障矿井的安全生产。

4 结 论

为确定煤矿应急管理体系中的薄弱环节，提出有针对性的应对措施，本文根据生产实践经验，确定影响应急管理体系的4个一级因素，17个二级因素，以层次分析法为基础，结合群决策和灰色理论，建立综合评价模型，并利用研究结果，对温庄煤业应急管理体系进行评价，找出影响最大的3个因素，为改善煤矿应急管理体系提供理论依据。