动力干扰下宽体客机机翼多目标优化设计

薛帮猛，张文升，孙学卫，吴宇昂

中国商飞北京民用飞机技术研究中心 民用飞机设计数字仿真技术北京市重点实验室，北京 102211

大型民用飞机机翼在产生升力的同时，阻力贡献也占到了全机一半，机翼的气动性能严重影响飞机的经济性。常规翼吊气动布局中，机翼、机身、发动机短舱、吊挂之间相互干扰，形成一个紧密联系的部件系统(简称WBPN构型)。20世纪90年代德国宇航院的研究显示[1]：吊装涵道比为8～9的涡扇发动机会使机翼超过60%翼展范围的升力显著损失，而吊挂也将造成内、外翼展向升力系数分布的不连续。文献[2]认为短舱/吊挂对机翼的干扰源于其诱导了额外的上、下洗作用。可以明确的是，真实飞机的机翼需要在比均匀来流复杂得多的条件下工作。与单独设计机翼或翼身组合体外形相比，在更接近全机外形的部件系统中优化设计机翼，对提高最终整机的气动性能更有意义。巴西航空工业公司Oliveira等[3]也指出了在飞机/发动机集成构型中优化设计部件外形的必要性。东京大学Nakahashi团队[4-7]使用伴随梯度优化方法进行了一系列针对WBPN构型的多点优化设计研究。最近，密歇根大学Martins团队[8]用梯度优化算法实现了支线机全机构型中机翼外形的优化设计。中国在飞/发集成构型的优化设计方面也做出了很多卓有成效的研究工作，左英桃等[9]使用伴随梯度优化方法在WBPN构型下，同时对DLR-F6的机翼和短舱实施了减阻优化设计。张宇飞等[10]尝试了用遗传优化算法在短舱干扰下实施机翼一体化设计。笔者所在团队[11]利用超级计算机和大规模并行计算，实现了在可接受的时间周期内完成NASA CRM(Common Research Model)飞/发集成构型下的机翼多目标优化过程。

除了机身、短舱和吊挂等有形部件的干扰，发动机喷流对机翼的影响同样不容忽视。模拟发动机进排气的流场中，在喷流的诱导作用下，其附近流场的速度大小和方向都将发生改变。翼吊气动布局中，发动机喷流不但增加喷流区内挂架上的刮擦阻力，对机翼下表面流动的加速作用会直接使升力损失，并间接增加巡航阻力。相比于窄体机，吊装更大涵道比和尺寸发动机的远程宽体客机，发动机喷流对机翼的气动干扰问题更为严峻。文献[12-16]在涡扇发动机喷流对机翼的干扰效应和气动性能影响方面做了大量研究。风洞试验中喷流干扰的研究手段主要是使用涡轮风扇模拟器(Turbofan Powered Simulators，TPS)[14-19]，但这种试验研究非常昂贵，不适合大量开展。另外，使用数值计算手段模拟发动机进排气时物面不封闭，直接由物面积分得到的阻力并不是真正意义上的机体阻力。此时，要将发动机推力和机体阻力划分清楚，需要经过较为复杂的推力/阻力分离计算[14-16]，这对喷流干扰下的机体减阻设计带来了挑战。

本文尝试直接在发动机喷流作用下开展宽体客机机翼气动外形的多目标减阻优化设计。首先，用动量定理分析动力短舱流场，选择合适的变量作为优化设计目标。接下来，以某宽体客机为对象，研究巡航工况下喷流对机翼气动干扰的程度，明确在喷流作用下设计机翼的必要性。最后使用前期建立的基于雷诺平均Navier-Stokes(RANS)方程计算分析和遗传算法寻优的多目标优化系统[11]，在CFD(Computational Fluid Dynamics)计算中以进排气边界条件模拟动力短舱，实施机翼外形的多目标优化设计。

1 动力外形流场分析和喷流干扰计算

CFD计算图1所示的动力短舱[14]绕流时，进排气模拟是通过边界条件来实现的，风扇入口处(E12)给定静压，风扇出口(E17)和核心机出口(E7)则给定总压比和总温比。图中VPre、VPost分别为上、下游远场速度大小；DPre、DPost分别为进、排气流管内物面积分阻力大小；φPre、φPost分别为进、排气流管表面积分阻力大小；DFrame为机体表面积分阻力大小。

图1 动力短舱流场控制体划分[14]Fig.1 Control volume division of powered-on nacelle flow-field[14]

对进、排气流管分别列流动方向动量方程，推导后可得推力区净推力FN和阻力区总阻力DExt的表达式，推力与阻力之差为

FN-DExt=(F17+F7-F12)-

(DFrame+DPre+DPost)

(1)

式中：F17+F7-F12为排气与进气边界上“毛推力”之差；DFrame+DPre+DPost则为整个流场中所有壁面积分流向力的大小，也即CFD计算直接给出的“阻力”，如前述因壁面不封闭它并不是真正的阻力。给定进排气边界和来流条件，仅修改机体外形时F17+F7-F12大小不会变。在机体部件减阻优化设计中，降低的无论是阻力还是推力损失，都会使推力与阻力之差增大，这正是期望的优化目标方向。此时FN-DExt和DFrame+DPre+DPost的变化量大小相等，因此以壁面积分流向力最小化为目标也是合理的。

本文中CFD计算使用内部CFD程序SFlow[11]，该程序在多块点对点结构化网格上以有限体积法求解雷诺平均Navier-Stokes方程。无黏通量项用Roe平均迎风通量差分分裂格式离散，黏性通量项用中心差分格式离散，时间推进计算采用隐式LU-SGS(Lower Upper-Symmetric Gauss Seidel)方法。SFlow有S-A(Spalart Allmaras)一方程和SST(Shear Stress Transport)两方程湍流模型，本文的CFD计算采用SST两方程湍流模型。MPI(Message Passing Interface)方式并行和基于贪婪算法的并行任务分配策略使SFlow有很高的并行效率。SFlow具有定升力计算功能，在迭代计算过程中，通过不断调整来流攻角，逼近设定的升力系数值。SFlow程序经过大量标准模型的验证计算，其计算精度也在很多工程项目中确认。图2展示了NASA CRM机翼-机身-水平尾翼构型的计算结果(图中Cp为压力系数，x/c为无量纲弦向位置)，机翼压力分布与NASA网站提供的风洞试验结果一致性良好。计算状态为：马赫数Ma=0.85，升力系数CL=0.534， 基于平均气动弦长的雷诺数Re=3×107。计算中使用了包含1 200万单元的网格，并且用网格变形方法使机翼计算外形的扭转变形与风洞试验中测得的变形量一致。

是否有必要直接在喷流作用下设计机翼，取决于喷流干扰程度。图3给出了某宽体客机的翼身组合体、机翼/机身/吊挂/通气短舱、机翼/机身/吊挂/动力短舱(分别简称WB、WBP+TFN、WBP+PN构型)外形，在马赫数Ma=0.85，迎角α=1.95°和基于平均气动弦长雷诺数Re=5×107状态下表面等压线的CFD计算结果。通气短舱(TFN)和动力短舱(PN)的外形面形状和流量系数相同。计算网格方面，3个外形的网格单元数都在1 000万左右(表1)，物面第1层尺度足以保证y+在1左右。WBP+TFN和WBP+PN的网格在机翼和机身周围的拓扑结构和点分布规律是一致的，该对比关注升力和压力分布，不做阻力的对比。

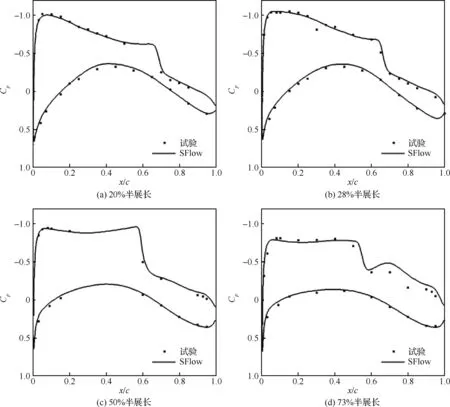
图2 NASA CRM机翼截面压力分布计算与试验对比Fig.2 Comparison of NASA CRM wing sectional pressure distributions between CFD calculation and test

图3 安装和喷流干扰下的机翼表面等压线图Fig.3 Contours of wing surface pressure coefficient under installation and jet effects

由图3可见，飞/发集成构型内翼为弱激波，去掉短舱吊挂后的WB构型内翼却表现为位置靠后的强激波。图4给出了内翼26%半展长位置机翼压力分布对比，在喷流作用下，内翼激波位置前移，且强度略有增加。图5对比了机翼展向升力系数分布(横坐标η为展向相对位置)，可以看到从WB到WBP+TFN，再到WBP+PN，机翼升力是逐步降低的。从表1可以定量地看到，安装通气短舱和吊挂后，升力系数损失了0.018，加入喷流后升力系数又损失0.021。如果最终配平后全机巡航升力系数为0.5，那么这两部分损失叠加高达全机升力系数的8%。因此，从干扰导致升力损失这个角度来说，翼吊布局宽体客机机翼气动设计不仅应该考虑短舱吊挂的安装效应，还应该考虑喷流干扰。

表1 发动机安装和喷流干扰下的升力系数Table 1 Lift coefficients under installation and jet effects of engine

图4 安装和喷流干扰下的机翼截面压力系数分布对比Fig.4 Comparison of wing sectional pressure coefficient distributions under installation and jet effects

图5 安装和喷流干扰下的机翼展向升力系数分布对比Fig.5 Comparison of wing spanwise lift coefficient distributions under installation and jet effects

2 优化设计方法

本节介绍优化设计中涉及的几何外形参数、计算网格生成、CFD计算和优化流程等方面。

优化设计的对象为WBP+PN构型下的机翼外形，具体来说是有限个机翼控制剖面。使用CST(Class function/Shape function Transformation)参数化方法[20-22]表达三维机翼外形，设计变量可以是控制剖面的扭转角或CST参数。该参数化方法具有一些设计者关心的直观参数，可直接显式控制翼型前缘半径、尾锥角和后缘厚度等几何特征。设计变量以扰动量的形式叠加到初始外形(Baseline外形)的基本参数上，基本参数需在优化开始前对初始控制剖面经过参数反算获得。

优化中使用网格变形技术实现新外形计算网格的快速生成。基于必要的网格收敛性研究，计算精度和时间的权衡，本文优化设计中使用包含445个网格块和1 065万单元的结构化网格。初始网格在ANSYS ICEM-CFD软件中生成，物面第1层尺度保证y+≈1，法向增长率为1.2。 这里的网格变形是与机翼参数化方法集成在一起的。给定一组机翼参数后，对于Baseline机翼表面的每一个网格点，根据其在平面形状中的展向、弦向位置，用参数化方法可以算出其在新机翼外形中的坐标。算出所有表面网格点的新坐标后也就生成了新的表面网格。接下来以指数衰减规律将表面网格角点的位移，传递到每个网格块的角点。最后用无限插值(TFI)方法插值逐步得到内部网格线、面、体新的空间坐标。同时，机翼厚度、容积等几何信息也都计算出来，这些量用来判断方案是否满足几何约束。

为了实现优化过程中的快速CFD计算评估，计算将以收敛好的Baseline外形流场解为初场，迭代计算扰动后外形的流场，同时使用多重网格和当地时间步长等加速收敛措施。经大量测试证明，用96核并行，10 min左右即可完成600次迭代，阻力系数和力矩系数的收敛程度可以满足要求。图6为有代表性的新外形阻力系数(CD)计算收敛历史(图中1 count表示阻力系数为0.000 1)。

本文以遗传算法为驱动，调动外形参数化、网格变形和CFD计算形成设计循环，实施多目标优化设计。优化流程如图7所示,每个新个体都是在Baseline外形的基础上，叠加由寻优算法给出的扰动量得到，表面网格也会随扰动相应变形。同时，新外形的几何特征也会被分析出来，并判断是否满足几何约束。如果不满足几何约束，该个体将被淘汰，不再进行后续的CFD计算分析。对于满足几何约束的个体，由计算结果判断是否满足气动约束，根据目标函数值判定个体优劣。完成一代种群的分析后，优化算法会生成新一代个体。本文的优化案例采用具备精英策略的非支配排序遗传算法NSGA-II[23]实现多目标寻优。

图6 阻力系数收敛历史Fig.6 History of drag coefficient convergence

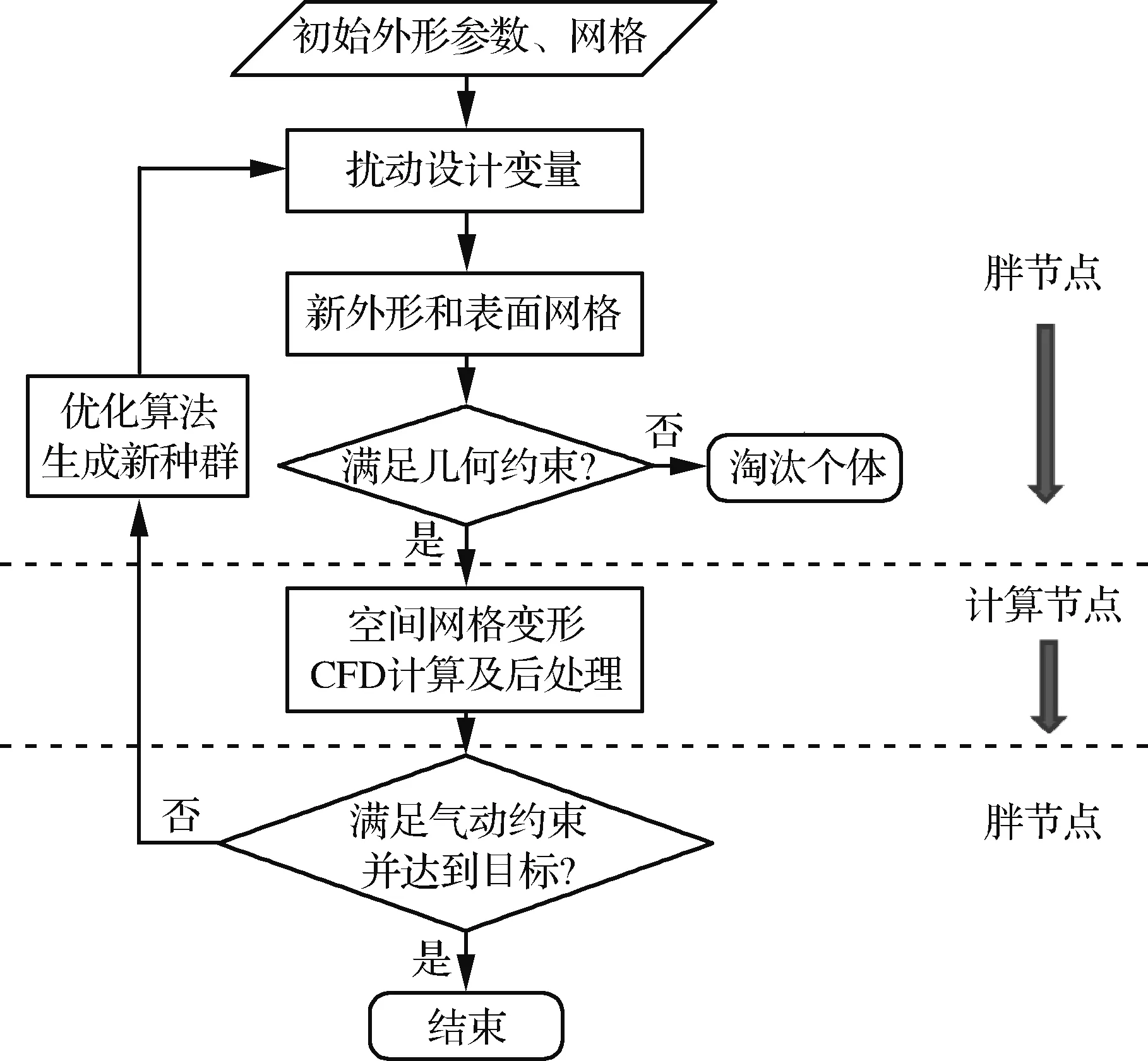
图7 优化设计流程Fig.7 Flow chart of optimization design

3 机翼优化设计

Baseline外形为前面计算的宽体客机WBP+PN构型，该方案在前期已经过初步人工修形设计，巡航马赫数为0.85时已有较为理想的升阻比和压力分布形态，但阻力发散性能不佳。下面将在此基础上优化机翼的扭转分布和剖面形状，在满足几何和气动约束下减小阻力。除了巡航马赫数为0.85的状态，还考虑马赫数为0.83、0.87两个状态。对本次优化设计的预期是：在保证马赫数为0.85时阻力不增的前提下，尽可能降低马赫数为0.87时的阻力，同时马赫数为0.83的阻力不高于马赫数为0.85的。

优化问题定义为：进行3点3目标优化，3个设计点分别为飞行马赫数为0.83、0.85和0.87，将每个设计点的壁面积分“阻力”作为独立的目标函数。设计变量包括9个控制剖面的扭转角和8阶CST参数共171个。设计约束有升力系数、低头力矩系数和迎角，其中升力系数的等式约束通过CFD程序的定升力计算实现。几何约束包括：剖面最大相对厚度为给定值；弦向15%、72%两处厚度不小于初始值的95%；油箱容积不小于初始值。

本次优化种群规模为512，初始种群在设计空间内随机产生。每批次同时对128个个体计算评估，每个个体串行计算3个设计点的气动性能。计算中同时使用共12 288核CPU的计算资源，CPU型号是英特尔Xeon E5-2692，时钟频率为2.2 GHz。在80 h内，完成接近20 000个个体的计算分析，遗传优化近40代。图8展示了优化过程中3个目标函数的演化历史，从下沿轮廓来看，马赫数为0.83、0.85下的两个设计目标已经趋于收敛，但马赫数为0.87目标函数值的下降趋势未尽。图9为马赫数为0.85和0.87两个目标函数值的散点分布图(图中Candidates代表已分析方案)，Pareto前缘上的方案数量还不够密集。图中蓝色方形标志为Baseline方案所在位置，综合考量3个设计点阻力系数、力矩系数、压力分布和几何展向过渡等因素后，在Pareto前缘上选定红色菱形标志的个体(ID19257)为此次优化的最优结果。相比于Baseline方案，最优解壁面积分流向力系数下降情况为：马赫数为0.83时增加2.0 counts， 马赫数为0.85时降低1.5 counts，马赫数为0.87时降低8.3 counts。可以选择马赫数为0.83阻力略有增加的方案是因为Baseline方案马赫数为0.83的阻力系数比马赫数为0.85的小3 counts左右。

图10为剖面优化后马赫数为0.85时机翼表面等压线分布与Baseline方案对比。尽管优化后阻力降低了，但机翼表面等压线沿展向分布较乱。事实上，由于自动优化中各个控制剖面拥有各自独立的自由度，加上进化类优化算法的随机性，优化后机翼几何展向过渡、等压线等值后掠、良好的压力分布形态很难同时保证。这里使用人工修形设计加以改进，修形原则是：在优化结果的基础上微调设计变量，保持激波强度和机翼展向升力分布基本不变，达到从翼根到翼梢剖面形状和压力分布渐进变化的效果。当然，这对设计者的经验和能力有较高要求。图11给出了人工修形设计后(Refined)的机翼表面等压线图，修形后，中外翼部分等压线基本上是等值后掠的，并且方案在气动性能上没有损失。

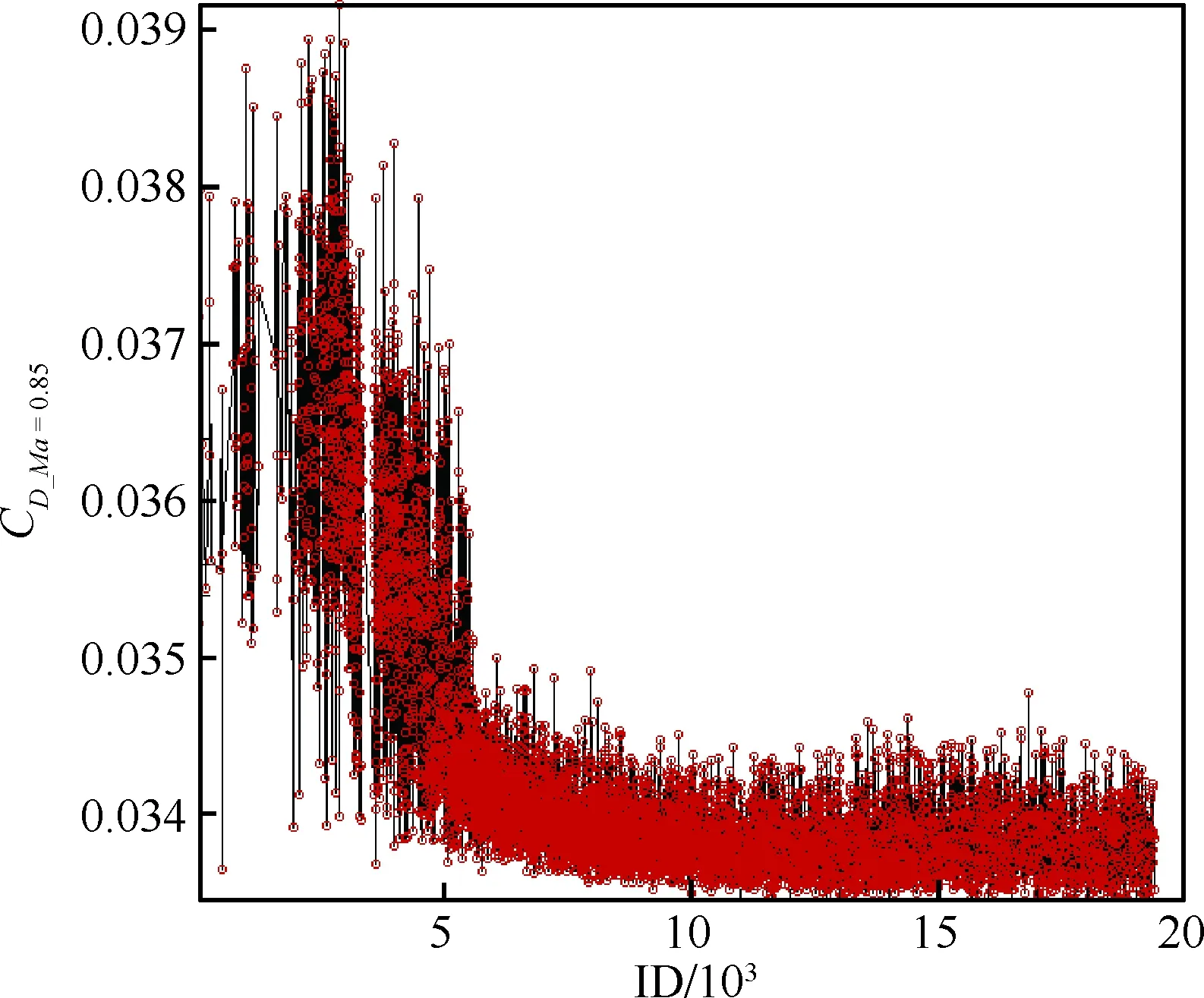
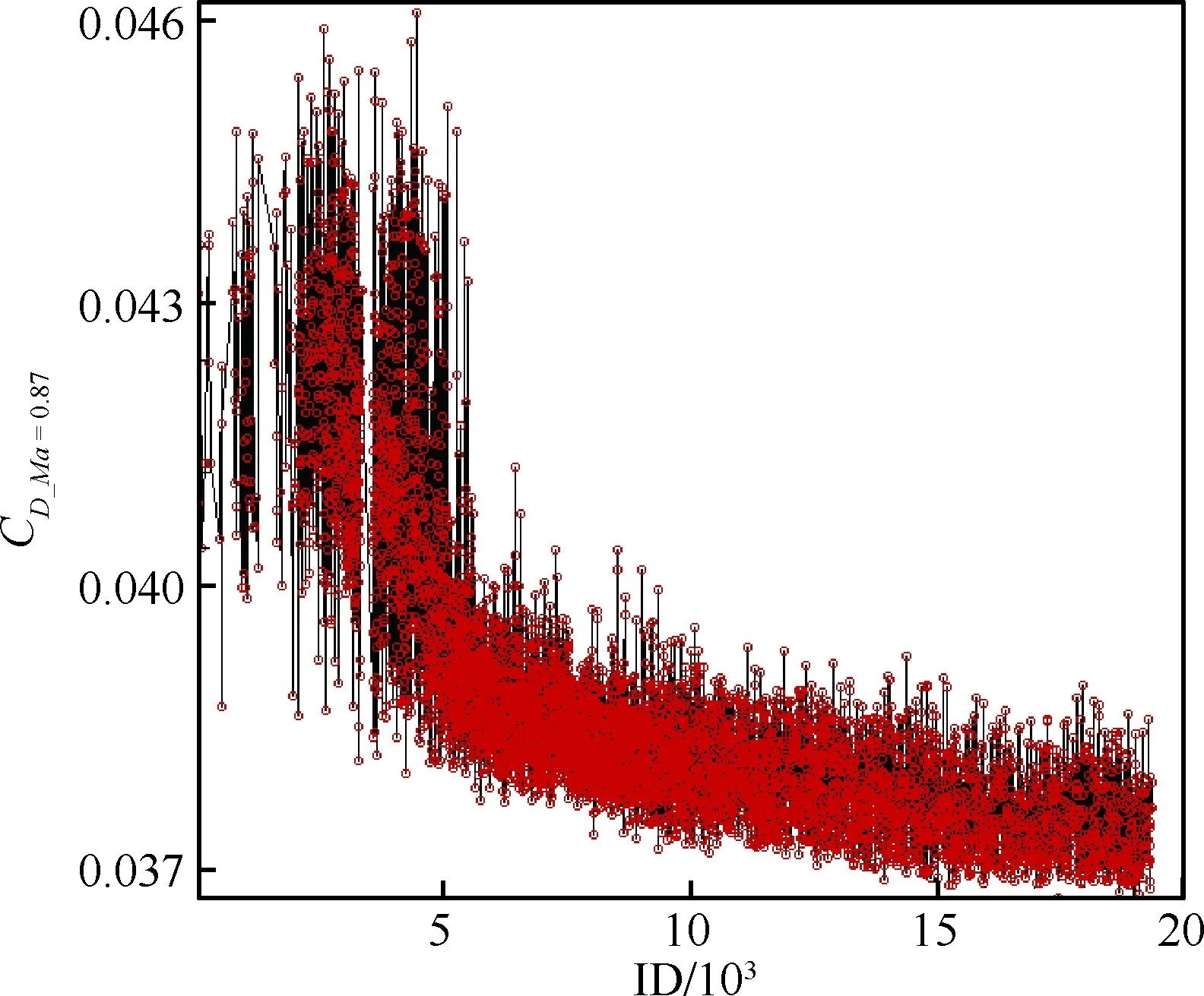
图8 优化过程中3个目标函数的历史Fig.8 History of three cost functions in optimization

图9 优化过程中两个目标函数的散点图Fig.9 Scatter diagrams of two cost function candidates in shape optimization

图10 马赫数为0.85时优化前后机翼表面等压线图Fig.10 Contours of wing surface pressure coefficient before and after optimization at Ma=0.85

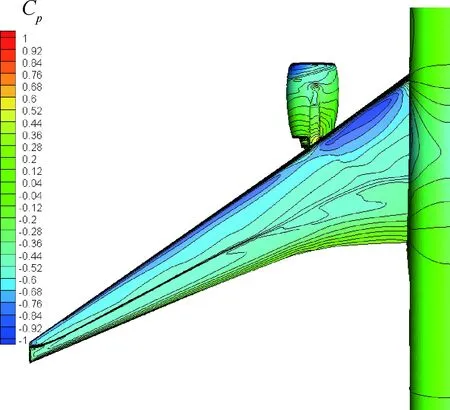
图11 人工修形后马赫数为0.85时机翼表面等压线图Fig.11 Contours of wing surface pressure coefficient after refinement at Ma=0.85

图12给出了机翼弦向15%、72%处相对厚度(t/c)和最大相对厚度沿展向分布的对比情况，优化和人工修形后机翼厚度基本无损失。图13对比了马赫数为0.85时优化前后4处剖面压力分布，其中前两处位于挂架内侧的内翼部分。优化后，激波在内翼略有前移和减弱，中段和外翼部分则显著前移和减弱，这有利于降低激波阻力。人工修形后，激波后流动的二次加速现象完全消失，压力分布形态较为理想。图14对比了马赫数为0.85 时机翼展向升力(升力系数CL与当地弦长c的乘积)分布，优化前后无明显变化。

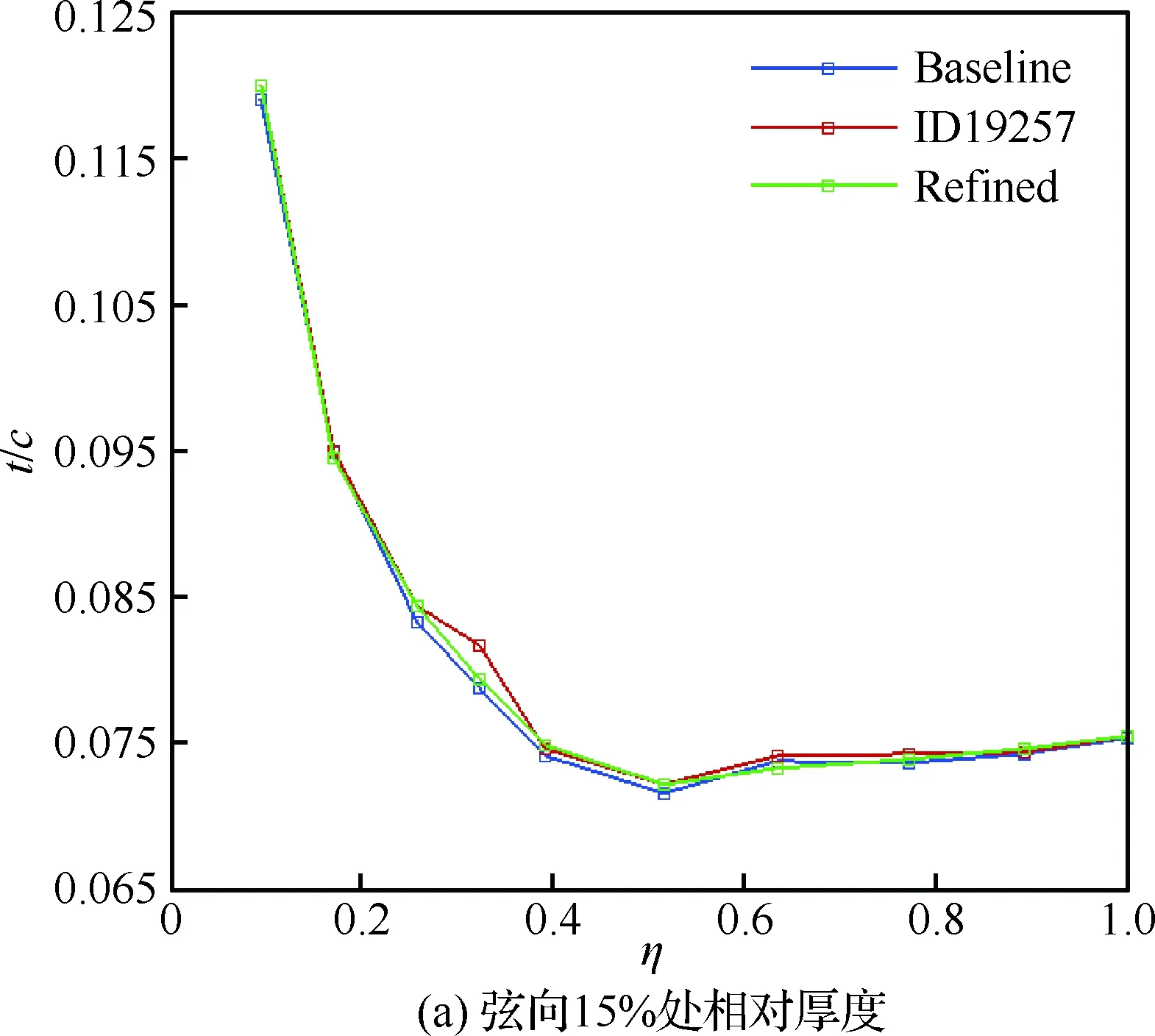
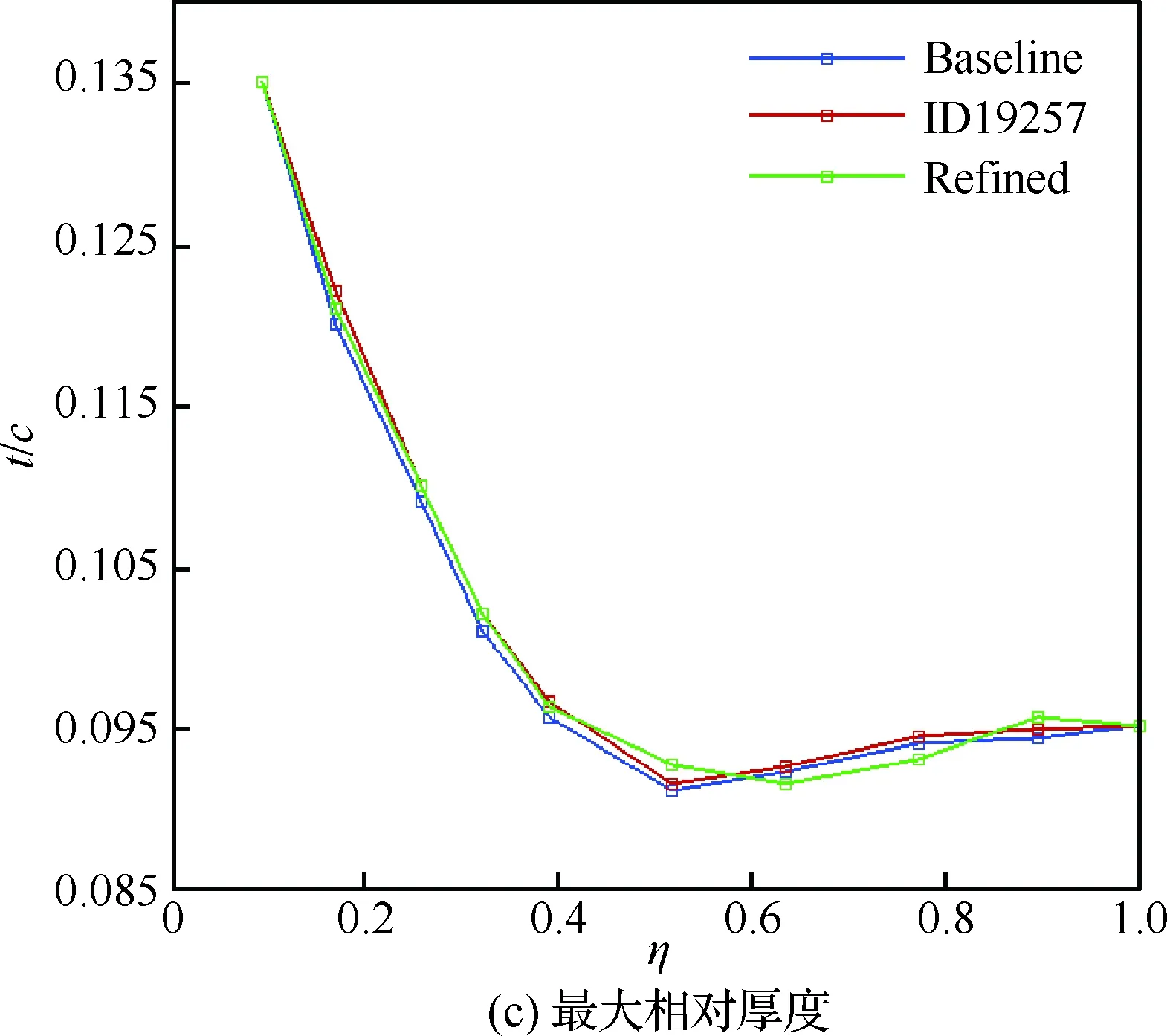
图12 优化前后机翼弦向3处厚度分布对比Fig.12 Comparison of distributions of wing thickness at three chordwise positions before and after optimization

为进一步验证优化取得的阻力下降效果，在优化加人工修形后的机翼上安装第2节中的通气短舱进行CFD验证计算。图15展示了马赫数为0.85时Baseline和人工修形后方案的表面等压线分布。图16对比了通气构型马赫数为0.87时优化前后4处剖面压力分布，优化加人工修形后的主要变化是吸力峰略有提高，激波前移并减弱。表2列出了安装PN和TFN条件下阻力的变化量，PN构型下为壁面积分流向力系数。马赫数为0.87时，两种条件下的阻力变化量基本一致，但马赫数为0.83和0.85时有差异，这样的差异源于优化设计中是否考虑喷流干扰。如前所述，优化前Baseline方案已在马赫数为0.85时具备理想的升阻比性能，因此阻力的下降不显著。总的来说，本次优化设计达到了预期效果，特别是在马赫数为0.87时，减阻高达全机阻力的3%。本次 优化过程持续80 h， 共消耗计算机时96 万核时。在精细设计阶段，以如此的时间和计算成本换取这样的性能收益是很有现实意义的。

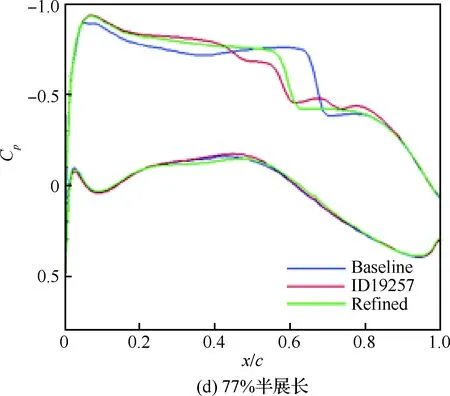
图13 马赫数为0.85时优化前后机翼剖面压力分布对比Fig.13 Comparison of distributions of wing sectional pressure at Ma=0.85 before and after optimization

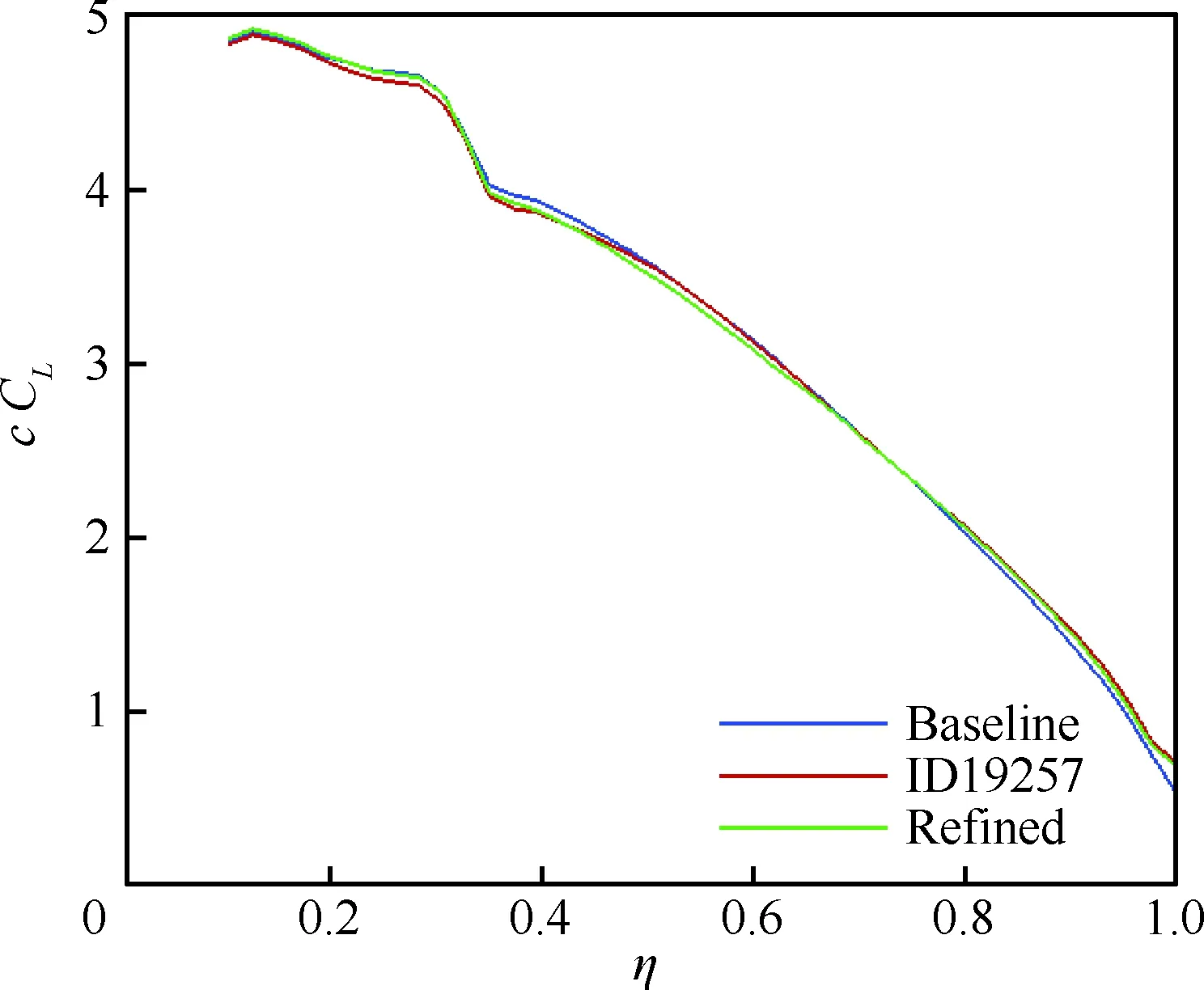
图14 马赫数为0.85时优化前后机翼展向升力分布对比Fig.14 Comparison of distributions of wing spanwise lift at Ma=0.85 befor and after optimization

图15 通气短舱下优化前后机翼表面等压线图对比Fig.15 Comparison of contours of wing surface pressure coefficient before and after optimization with TFN integrated

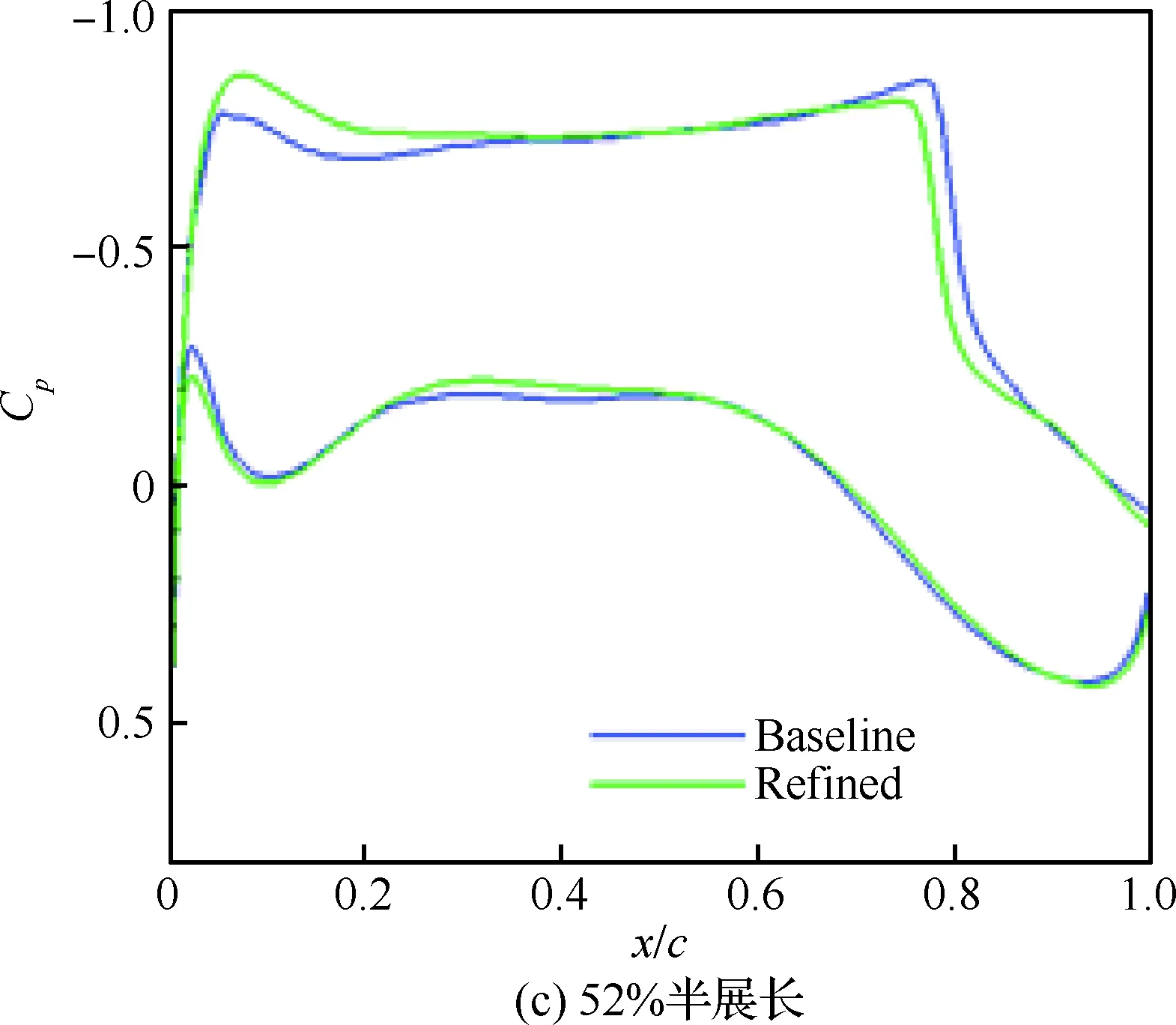
图16 马赫数为0.87时优化前后机翼剖面压力分布对比Fig.16 Comparison of distributions of wing sectional pressure at Ma=0.87 before and after optimization表2 机翼优化后阻力系数变化量Table 2 Variation of drag coefficient after wing shape optimization

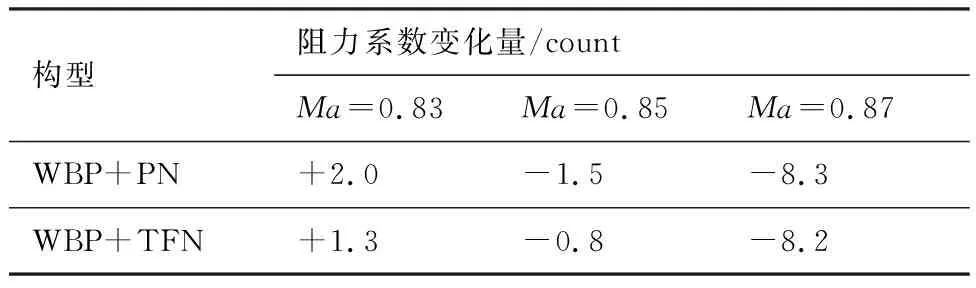
构型阻力系数变化量/countMa=0.83Ma=0.85Ma=0.87WBP+PN+2.0-1.5-8.3WBP+TFN+1.3-0.8-8.2

4 结 论

1) 应用动量定理分析动力短舱流场的进排气流管和外部流动，明确了机翼外形优化设计中以推力与阻力之差最大化或壁面积分“阻力”最小化为目标的合理性。

2) 以宽体客机Baseline机翼方案为对象，研究了短舱/吊挂以及喷流的干扰作用。CFD计算结果显示，从WB到WBP+TFN，再到WBP+PN，机翼升力因受干扰而逐步损失，且喷流引起的升力损失大于短舱/吊挂。从升力损失角度看，翼吊布局宽体客机机翼气动设计应该同时考虑短舱吊挂的安装效应和喷流干扰。

3) 运行前期搭建的优化系统，80 h内完成了近20 000个设计方案的计算评估，遗传优化近40代。在满足所有约束条件的前提下，选择的最优方案在取得马赫数为0.87时阻力系数下降超过8 counts的同时，也使马赫数为0.85时的阻力略有降低，阻力发散性能明显提高。人工修形设计后，机翼几何展向过渡和压力分布形态更为理想，且气动性能无损失。动力构型下取得的减阻成果，在通气短舱构型下得到了进一步验证和确认。