建模竞赛背景下数学建模课程教学创新探究
孙 欣, 李晓雪
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
《数学建模》是数学专业学生于大二下学期开设的专业选修课程,是近年来一项成功的大学数学教学改革实践。将数学建模引入大学教育,为学生学习数学和解决外部世界问题提供了一种新的方式和工具。将数学知识用于实际生活,使学生有更多机会参与发现和创造的过程,取得在传统课堂里和书本上较难获得的实践经验和切实感受。数学建模一方面激发学生获得较广博的数学知识、独立研究的主动性;另一方面培养学生想象力、洞察力、深入实际调查研究的能力,有助于在知识、能力及素质等方面迅速成长[1]。有关《数学建模》课程研究及相关活动的开展取得许多成果[2-6]。大学生数学建模竞赛是高校开展的一项学科竞赛活动,为提高学生用数学建模方法分析、解决实际问题的能力搭建了广阔的平台,有益于培养创新精神、团队精神和综合素质人才。
将数学建模竞赛的思想和方法有机地融入《数学建模》课程教学中去,是一种教学研究与实践的探索,已取得相关的研究成果[7]。2017—2019年,在本科数学与应用数学专业2015级、2016级、2017级分别进行了基于建模竞赛背景下的《数学建模》课程实践教学创新研究与探索。课程改革(简称课改)的主体目标是将数学建模竞赛内容引入数学建模课程,使其更具实效性。
新的教学模式在教学体系、课程组织形式及内容方法等方面较传统的教学模式主要区别体现在5个方面:一是在《数学建模》课程内容设置中增设《数学实验》课程中基础且重要的内容,将计算机技术引进《数学建模》课堂;二是突出学生实践环节,让学生自愿结合组成学习小组,合作完成课程任务,课程评价以小组为基础,结合个人表现;三是课程内容与数学建模竞赛紧密联系,进行历年建模国赛真题讲评与竞赛经验交流,理论与实践相结合;四是充分发挥信息技术优势,组建课程QQ群,增加课下与学生互动,克服时空带来的不便性,保持课程内容学习的连续性;五是课程考核评定取消期末考试,取而代之,采取以小组成绩为基础结合个人表现、课程学习结合竞赛实践两结合原则评定学生的期末成绩,考核评定具有开放式。总结3个年级的基于建模竞赛背景下的《数学建模》课程的实践教学经验,对于探索研究一种新的课程教学模式,起到了积极的推动作用。
1 课改实践创新的必要性
1.1 传统的《数学建模》课程教学模式存在弊端
1) 教师一言堂。教师授课满堂灌,学生被动接受新知识、课堂参与度小、缺少利用数学模型解决实际问题的实践机会。
2) 学生一言堂。一堂课只有一个学生作主讲,缺少以教师为主导的课堂组织调控。如果主讲学生水平有限或是准备不足,会造成大多数学生学无所获,浪费宝贵的课堂时间。
1.2 课程内容设置与建模竞赛无关联
对14级选修《数学建模》课程的部分学生做过调查,学生对课程的反馈意见之一是所学内容与建模竞赛几乎无关联,使学生有学无所用的学习无力感。
2 课改实施方案
2.1 课前充分了解学生对课程的心理预期,及时调整课程内容设置
在2018年课程第一节对2016级数学与应用数学专业一个选课班50名学生调查:《数学建模》课程期望是什么?课程建议有哪些?调查结果如表1所示。

表1 2016级学生选修《数学建模》课程期待与课程建议Table 1 Expectation and advice on mathematical modeling course of students enrolled in 2016
在2019年课程第一节对2017级数学与应用数学专业一个选课班47名学生关于选修《数学建模》课程动因和期待展开调查,结果如表2、图1所示。
通过对学生《数学建模》关于课程期待、选课动因及课程建议3个方面的调查,利于教师对课程内容的设置进行及时地整改、优化,有利于突出学生学习的主体地位,发挥教师教学的主导地位。

表2 2017级学生选修《数学建模》动因与课程期待Table 2 Motive and expectation of mathematical modeling course of students enrolled in 2017
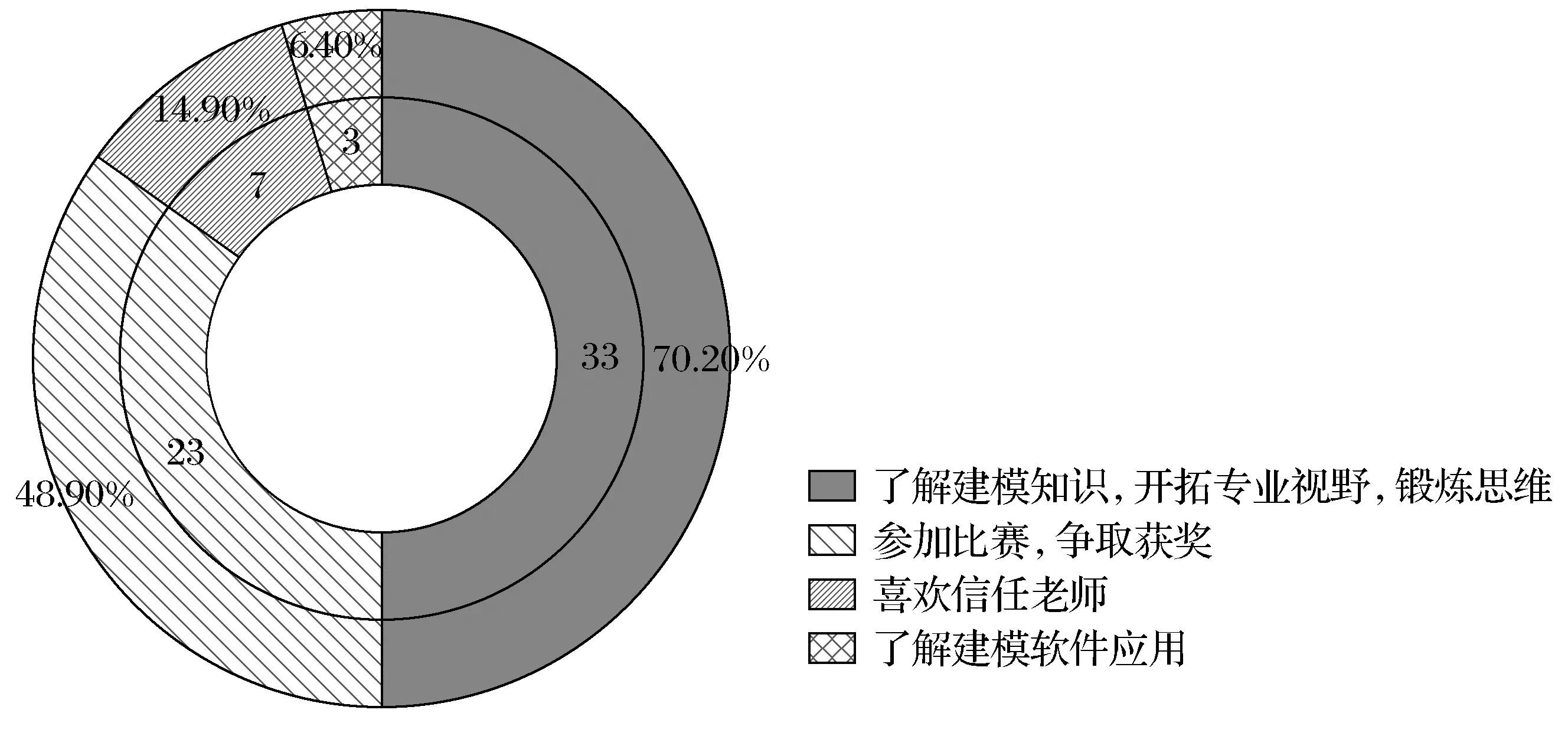
图1 2017级学生选修《数学建模》动因调查Fig.1 Motive investigation into mathematical modeling course of students enrolled in 2017
2.2 课程内容设置多元化
《数学建模》课程共54学时,4学时/周,13周半教学周。教学内容分成5个部分:一是基本数学模型学习;二是数学建模算法与程序学习;三是数学实验基本内容学习;四是建模竞赛指导与培训;五是以学生为主体的建模经验分享与交流。
1)基本数学模型的学习。参考姜启源等编著的《数学模型》第四、五版[1,8]。以评价类模型(理想解法TOPSIS、主成分分析法PCA、层次分析法AHP、秩和比法RSR)、预测类模型(微分方程模型、灰色理论模型、时间序列模型、马尔科夫模型)、数理统计模型、规划类模型(线性规划、非线性规划、排队论、目标规划、动态规划)为基本学习内容。具体内容如表3所示。

表3 基本数学模型学习内容Table 3 Study content of basic mathematical model
2) 数学建模算法与程序学习。参考司守奎等编著的《数学建模算法与应用》[9-10],掌握基本算法和计算机实现的相关源程序。求解模型实质上就是算法的实践,一般是用Matlab,lingo,spss等数学软件来求解;而有些算法数学软件往往无能为力,需要用C/C++来编制程序解决。学习往往从模仿开始,指导学生从读懂算法程序的源代码开始,由浅入深,直至自己能上手编程,达到求解模型的目的。
3) 数学实验基本内容的学习。将Matlab计算及仿真基础引入数学建模课程,内容有Matlab简介、Matlab数值计算、Matlab图形功能、Matlab符号计算功能、Matlab程序设计与数据拟合等。掌握建模必备的计算机技术,实现计算、绘图、数据分析等操作。
三是丰富业余生活,加强企业文化建设。通过举办群众广泛参与的读书学习、健身娱乐活动等,让单位处处充满生机活力,处处洋溢文化气息。
4) 建模竞赛指导与培训。梳理整理历年数学建模竞赛试题,统计分析近10年的国赛常考数学模型。结合获奖论文,分析各种模型的应用,总结归纳数学建模常用算法及计算机实现。使学生掌握建模竞赛必备的论文写作、模型选择、算法与程序实现等相关知识。课程进行期间经历每年4月20日—5月10日持续约20 d的东北三省数学建模竞赛。鼓励学生积极参与竞赛,增加实践机会。赛前培训指导,赛后总结交流。结合数学建模竞赛,深化课程内容。
5) 以学生为主体开展建模经验分享与交流。建模是一个积累的过程,既有学习资料、信息检索收集的积累,又有建模竞赛实战比赛经验的积累,缺一不可。开课伊始,请有丰富建模经验并在各类建模竞赛中多次获奖的学长、学姐做主题为“浅谈数学建模与经验分享”的报告会,围绕什么是数学建模、数学建模一般步骤、前期知识储备、比赛经验等方面进行经验分享,充分彰显榜样的力量。这样的交流使缺少建模知识和建模经验的学生对建模及竞赛有一个全局和概括性的认知。课程进行中,结合刚结束的东北三省数学建模竞赛组织学生以小组为单位进行赛题讲解、思路分析,总结建模写作经验,这些实践环节利于增长建模的实战经验。
2.3 课堂组织形式
克服以教师讲解为主,学生被动接受新知识的传统教学模式,建立以教师为主导,学生为主体的课堂教学形式。利用QQ群加强师生互动与交流,让学生组成学习小组协作学习,进行多模块教学模式,采用这些组织形式有效地组织了教学,提高了教学效果。
1) 建立课程QQ群,以克服由时空带来的与学生的互动不便性,充分发挥QQ群的便捷性,与学生增加课程交流,改善互动模式,提高学习效率。
2) 将50名学生以自愿结合原则按照2~4人为单位组成15~17个学习小组,以小组为单位课上讨论、完成作业、考核评定,增强研讨合作的团队意识,为建模竞赛做好准备。
3) 建立多模块课堂教学模式。讲授与讨论相结合,根据课程内容不同,采取不同的模块进行教学,有效整合教学资源,对资源进行合理的筛选、组合和利用,起到了事半功倍的教学效果。
2.4 课改的特色与创新
将建模竞赛训练与指导引入《数学建模》课程中,深化了课程内容。进一步,为满足建模竞赛对计算机技术的要求,将《数学实验》课程的部分内容引入课程。结合《数学建模》课程基本教学目标和任务要求,将基本数学模型、数学建模算法与程序、数学实验[11]、数学建模国赛真题讲解[12-15]几部分内容有机结合、整合与优化。
1) 适度挑战学生能力
如果一个学习任务很简单,会很无聊;如果一个学习任务很艰巨,会很令人沮丧。数学建模的学习与竞赛有足够的难度构成一个挑战,又不至于伤害学生尝试的意愿程度,让学生在最适当的挑战下,更有可能投入到学习与竞赛中。
2) 创立学习共同体
《数学建模》课程的学习、考核以小组为单位进行,增加师生之间、学生之间互动机会与交流。让所有的学生都参与讨论,所有的成员交换信息、想法和观点。有利于加强合作学习、协作学习、团队学习和问题导向学习。
3) 培养批判性、创造性和对话式思维
建模过程往往通过提出问题让学生认识并改善自己的思维方式,使学生获得对问题进行批判性思考的能力,培养创造性思维,鼓励对话式思维。
4) 课程动态监测
开课伊始,以问卷调查的方式了解学生对课程的心理需求和期待。根据学生实际情况调整教学目标、制定切实的教学手段、选择合理有效的课堂组织形式。课程中期,继续问卷调查,征求学生意见,了解课程教学效果,调整、优化。课程结束前,无记名形式征求课程建设性意见,为下次教学改进提供参考依据。
3 课改成果
讲授《数学建模》课程的3年中,学期期末学生的评价反馈良好,满意度在96%以上。指导学生参加东北三省数学建模竞赛、全国大学生数学建模竞赛和美国大学生数学建模竞赛(2018年指导2组获得美赛二等奖)获奖情况如表4~表7所示。

表4 2017年全国大学生数学建模竞赛指导学生获奖情况Table 4 Guidance for students on award for national university mathematical modeling contest in 2017

表5 2018年全国大学生数学建模竞赛指导学生获奖情况Table 5 Guidance for students on award for national university mathematical modeling contest in 2018

表6 2019年全国大学生数学建模竞赛指导学生获奖情况Table 6 Guidance for students on award for national university mathematical modeling contest in 2019

表7 2017—2019年东北三省数学建模竞赛指导学生获奖情况
注: 表7中“占比”指本人指导学生获奖的组数与全校获同级别奖项的组数之比。
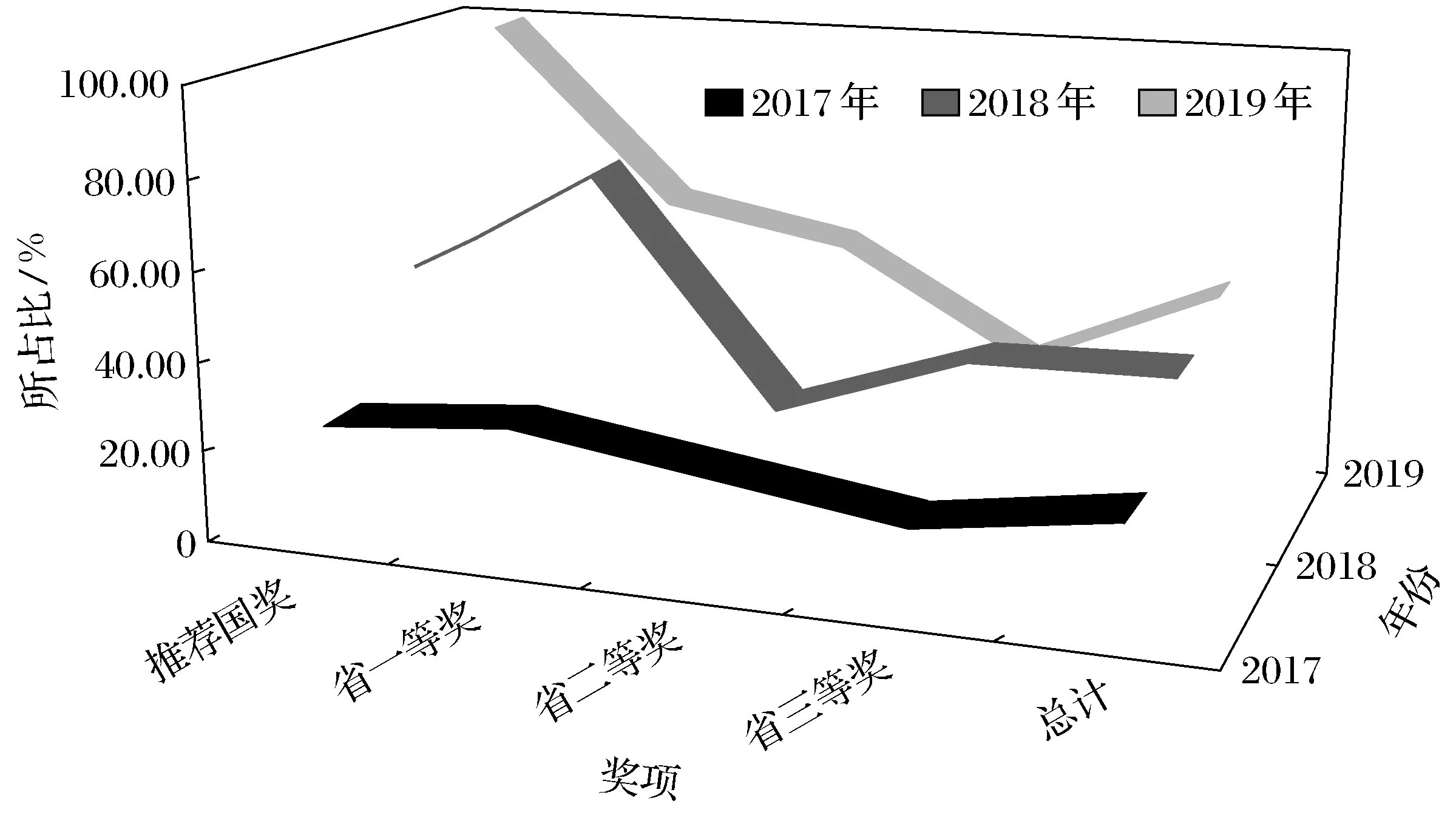
注: “占比”指本人指导学生获奖的组数与全校获同级别奖项的组数之比图2 2017—2019年指导全国大学生数学建模竞赛学生获奖所占比Fig.2 Award ratio of guidance for students for national university mathematical modeling contest from 2017 to 2019
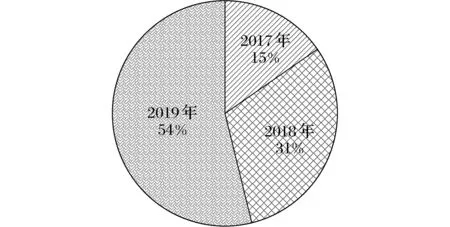
注: “占比”指本人指导学生获奖的总组数 与全校获奖总组数之比。图3 2017—2019年指导东北三省数学 建模竞赛学生获奖总数所占比Fig.3 Total award ratio of guidance for students for northeast three provinces mathematical modeling contest from 2017 to 2019
4 结论与展望
历经3年基于数学建模竞赛背景下的《数学建模》教学实践的探究初见成效,体现在学生对课程评价满意度和课程对数学建模竞赛的指导2方面。结合每学期期末学生对课程建设反馈意见的调查和授课实践,今后的课程建设还有需要提升的空间,具体体现在分层次教学、整合和优化课程资源、计算机软件的应用和编程3个方面。数学建模以数学作工具与外界世界联系起来,用数学解决实际问题,将数学应用于实践的能力与学生的数学基础有关。在今后的课程教学中可以考虑根据学生数学基础的差异实行分层次教学。依照教学大纲,《数学建模》课程只有54学时,而在54课时中完成实际教学内容达到预期教学目标,就必须对课程各部分资源进行调整、重组与优化。计算机技术的实现为数学建模教学内容和方法带来新启示,各种计算机软件和编程对于模型求解、算法实现等方面起到了关键作用,同时对教学也提出新的挑战。

