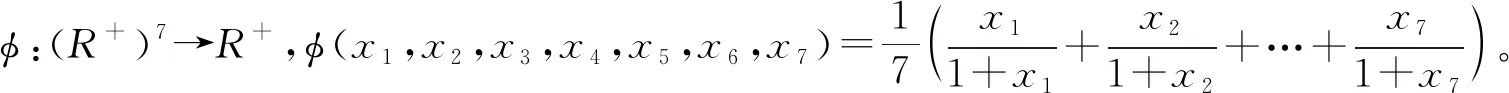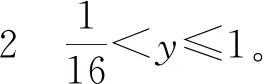关于3个映射的公共重合点定理
郝 妍, 关洪岩
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
度量空间中的不动点理论是非线性泛函分析研究的重点问题之一,而巴拿赫压缩映像原理是度量空间中关于不动点理论研究的最主要成果之一。从1922年巴拿赫在文献[1]中提出并证明压缩映像原理后,许多学者将此结果作了大量的推广并将其应用,得到了许多优秀的成果。其中,Czerwik[2]引入了b-度量空间的概念,并在该类空间中得到了新的不动点结果。随后,许多学者得到了关于b-度量空间中各式各样的单值和多值映射的不动点定理。Aydi等[3]证明了满足弱φ-压缩条件的单值和多值映射的公共不动点的结果。受文献[4]启发,Pacurar[5]给出了φ-压缩映射具有公共不动点的存在性和唯一性条件。利用相容映射给出压缩条件,文献[6]得到了2个映射具有公共不动点的结果。关于b-度量空间的一些新结果见参考文献[7-10]。
重合点问题是不动点理论研究中的另一类重要问题。在度量空间中,Machuca[11]得到了一对真映射具有公共重合点的条件。随后,Khan[12]和Liu[13]将上述结果进行了推广,证明了3个真映射在特定的条件下具有公共重合点。在文献[14]中,Liu等讨论了4个映射具有公共重合点问题。
受上述文献中结果的启发,本文主要讨论从T1拓扑空间到b-度量空间上的3个映射具有公共重合点的条件。首先,给出了从T1拓扑空间到b-度量空间上的关于3个映射的新型φ-压缩条件,在特定条件下,证明了3个映射具有公共重合点的定理。然后,针对所得结论,给出相应的例子说明其应用。
1 预备知识

为了得到主要结论,首先引入一些基本概念和引理。
定义1[2]设X是非空集合,映射d:X×X→R+。若∀x,y,z∈X满足条件:
1)d(x,y)=0当且仅当x=y;
2)d(x,y)=d(y,x);
3)d(x,y)≤s(d(x,z)+d(y,z))。
其中s≥1为常数。则称(X,d)为b-度量空间,s为b-度量空间的系数。
注1: 当s=1时,b-度量空间为通常的度量空间。
注2: 在文献[6]中作者举例说明了当s>1时b-度量空间不是度量空间。
定义2[6]设{xn}是b-度量空间(X,d)中的一个点列。
1) {xn}称为是收敛的是指存在x∈X满足当n→∞时,d(xn,x)→0;
2) {xn}称为是柯西列是指当n,m→∞时,d(xn,xm)→0。
b-度量空间(X,d)是完备的,是指该空间中的柯西列都收敛。
引理1[15]设φ:R+→R+为上半连续且递增函数,则对t>0,φ(t) 本节中主要讨论3个映射具有公共重合点的条件。 定理设X是满足第一分离公理的T1拓扑空间,(Y,d)是完备的系数为s≥1的b-度量空间。映射A,B,S:X→Y满足AX∪BX⊂SX,且下列条件之一成立: (a1) 映射A和S是连续的,同时A是真映射,AX是闭的; (a2) 映射A和S是连续的,同时S是真映射,SX是闭的; (a3) 映射B和S是连续的,同时B是真映射,BX是闭的; (a4) 映射B和S是连续的,同时S是真映射,SX是闭的。 若对任何的x,y∈X,存在φ∈Φ满足 则存在X中的一点u,使得Au=Bu=Su。 证明 任取X中的点x0,由于AX∪BX⊂SX,从而存在X中的点列{xn}及Y中的点列{yn}使得 y2n+1=Sx2n+1=Ax2n,y2n=Sx2n=Bx2n-1,n≥1 对点列{yn},若存在某个n∈N使得yn=yn+1,则可以得到公共重合点。事实上,当n=2k时,由压缩条件(1),可以得到 假设d(y2k+1,y2k+2)>d(y2k,y2k+1)=0,由φ的单调性及b-度量的三角不等式性质,有 矛盾。故d(y2k+1,y2k+2)=0,于是y2k=y2k+1=y2k+2。结合{yn}的定义,可以得到Ax2k=Bx2k=Sx2k,即有x2k为公共重合点。 当n=2k+1时,即y2k+1=y2k+2,利用类似的讨论可知x2k+1是映射A,B,S的公共重合点。 下面设d(yn,yn+1)>0,∀n∈N,去证明 (2) 分2种情形: 情形1n=2k,k∈N。 在压缩条件(1)中令x=x2k,y=x2k-1,有 假设d(y2k,y2k+1)>d(y2k,y2k-1)。由上式可知 矛盾。从而可得d(y2k,y2k+1)≤d(y2k,y2k-1)。利用式(3),可以得到 情形2n=2k+1,k∈N。类似于情形1的讨论,可以推出 (4) 下面将证明点列{yn}是Y中的一个柯西列。为此,只需证明子列{y2n}是Y中的柯西列。假设{y2n}不是柯西列,则存在ε>0,∀k∈N,存在2mk>2nk>k,且2mk为超过2nk的最小正整数,使得 d(y2mk,y2nk)≥ε (5) 和 d(y2mk-2,y2nk)<ε (6) 利用b-度量的三角不等式性质和不等式(6),可以推出 ε≤d(y2mk,y2nk)≤sd(y2mk-2,y2nk)+s2d(y2mk-2,y2mk-1)+s2d(y2mk-1,y2mk) 。 根据不等式(4),在上式中取k→∞的上极限 (7) 类似的,由ε≤d(y2mk,y2nk)≤sd(y2mk,y2mk-1)+sd(y2mk-1,y2nk)可知 另一方面,由d(y2mk-1,y2nk)≤sd(y2mk-1,y2mk)+sd(y2mk,y2nk)及不等式(4)可知 于是 (8) 经过类似的计算,可以推出 (9) 根据压缩条件(1),可以得到 利用不等式(5)、(8)和(9),在上式两边取k→∞的上极限,有 这是矛盾的。从而有Au=Bu=Su,即u为A,B,S的公共重合点。同理可证在条件(a2)、(a3)、(a4)其一成立时,映射A,B,S具有公共重合点。证毕。 在本节中给出一个例子来说明定理1的应用。 例设X=[0,1],定义其上的度量为d*:X×X→[0,+∞),d*(x,y)=|x-y|。设Y=[0,1],定义其上的b-度量为d:Y×Y→[0,+∞),d(x,y)=|x-y|2,系数为s=2。定义X到Y上的映射A,B,S分别为 即压缩条件(1)成立。2 主要结果







3 应用举例