具有规整曲率线网的光滑曲面设计

郑荟莹，伯彭波



具有规整曲率线网的光滑曲面设计

郑荟莹，伯彭波

(哈尔滨工业大学(威海)计算机科学与技术学院，山东 威海 264209)

为了设计具有规整曲率线网且无脐点的光滑曲面，提出一种曲面交互设计算法。采用Bézier曲面片光滑拼接构成的复合曲面作为表达形式，通过交替曲率线网的优化和曲面细分得到自由形状的设计曲面，所得曲面具有规整曲率线网而且没有脐点。以此复合Bézier曲面为基础，通过圆纹样条曲面优化算法得到结构规整的圆纹样条曲面，同时也能得到圆锥曲面条模型以及曲面多层支撑结构等自由建筑曲面设计中有重要应用的几何结构。

曲率线网；圆纹曲面；脐点；曲面设计

1 相关工作

在建筑曲面设计和数控加工等领域设计曲面上的曲率线具有重要的实际应用意义，例如在建筑曲面造型中，多层玻璃结构建筑物的支撑框架的走向必须与曲面的曲率线走向一致[1]，因此在应用中希望设计曲面的曲率线分布比较规整。规整的曲率线网是指曲率线分布比较整齐，而且曲率线网不含有奇异点。设计具有规整曲率线网的曲面难点之一是曲面的曲率线网对曲面形状变化高度敏感[1-2]。图1给出了一个参数曲面和曲面上的不规整的曲率线网，形状简单的曲面上具有很复杂的曲率线网。

现有曲面建模技术关注曲面的光顺性、连续性和逼近误差等要求，无法设计具有规整曲率线网且无脐点的连续参数曲面。已有的改善曲面光顺性的工作也能够在一定程度上改善曲面的曲率线分布，但不能保证得到具有规整曲率线网且无脐点的曲面。此类方法通过优化定义曲面上的能量函数改善曲面的光顺性[3]。JOSHI[4]通过极小化曲面的曲率变化达到光顺曲面的目的。一些方法通过直接或间接修改曲面上的高光线缺陷消除曲面的局部不光顺形状特征[5-7]。ALLIZE等[8]提出基于曲面上曲率线网的重新网格化方法，且不试图改善曲面的曲率线分布也无法去除脐点。KNÖPPEL等[9]提出网格曲面方向场的设计方法，可将主曲率方向作为约束生成沿曲率线的重新网格化结果，但该方法不能保证生成无脐点的曲面。LIU等[1]提出离散曲率线网格的计算方法，并讨论了在建筑曲面设计中的应用。PAN等[10]提出了基于曲面片边界上给定的方向场生成边界内部的光顺方向场，进而生成网格曲面的方法。

图1 曲面上不规整的曲率线网

本文提出一种能够生成具有规整曲率线网且无脐点的连续曲面设计算法。结合圆纹曲面优化技术得到具有规整结构的圆纹样条曲面及其他在建筑曲面设计中有重要应用的特殊几何结构。圆纹样条曲面采用Dupin圆纹面上的曲面片光滑拼接构造复杂的形状[11]。圆纹样条曲面由圆弧样条曲线组成，是曲面上的精确曲率线，在一定程度上实现了几何表达和曲率表达的一致性。圆纹样条曲面几何性质的表达，在面向数字化制造中的曲面设计中具有重要的应用前景[12]。

圆纹样条曲面建模的困难在于其自由度很少，传统的方法无法生成具有复杂形状的圆纹样条曲面。SRINIVAS等[13]首先设计一个圆圈网格，在网格的指定顶点上定义一个标架，并通过反射约束传播到整个曲面，但不能保证曲面的整体光顺性。BO等[11]提出一种全局观点的优化方法，将网格顶点和顶点上的标架一同优化，可以构造形状复杂的圆纹样条曲面。该方法在目标曲面上沿曲率线生成四边形网格，网格结构比较复杂且存在奇异点。

本文的贡献为：①提出一种无脐点且具有规整曲率线网的光滑曲面设计方法；②提供了具有规整结构的圆纹样条曲面、圆锥曲面条模型及多层支撑结构等自由建筑支撑结构等自由曲面建筑设计中重要的几何结构设计方法。

2 算法描述

本文提出的曲面设计方法，能够设计具有规整曲率线网的光滑曲面。在曲面细分的设计流程中，用户首先设计一个粗糙网格，表达设计意图，然后通过迭代曲面细分和曲面优化得到光滑的曲面。

为了在曲面设计过程中提供一个光滑的曲面表示，本文以三次Bézier曲面拼接的复合曲面作为曲面表示形式，优化目标使Bézier曲面片的边界曲线成为曲面上的曲率线，并由所有曲面片的边界曲线构成复合曲面上的曲率线网结构。最后基于具有规整曲率线网结构的复合Bézier曲面，设计圆纹样条曲面优化算法优化Bézier曲面的控制点，生成圆纹曲面片的有理二次多项式曲面的控制点和权重。

目标是让复合曲面中Bézier曲面片的边界曲线成为曲面的曲率线，基本策略是通过交替曲面细分和曲率线优化构造具有规整曲率线网的自由曲面，并以此曲面的几何信息构造圆纹样条曲面优化的初始。算法流程如图2所示。首先交互设计初始网格并生成初始Bézier曲面。然后交替2个步骤：基于Bézier曲面片的规整曲率线网以及曲面细分。当得到的曲面符合设计要求时，优化复合Bézier曲面的控制点生成圆纹样条曲面。

图2 算法流程图

初始设计网格是规整四边形网格结构，网格细分可保持四边形网格结构，曲面优化的目标是网格面片的边界成为曲面的曲率线。由于圆纹曲面片没有脐点，因此算法可以保证最后生成的圆纹样条曲面符合设计意图并且具有规整曲率线网结构。

2.1 初始曲面的交互设计

首先交互设计一个符合预期形状的粗略四边形网格曲面。每一个四边形内生成3×3个小四边形，小四边形的顶点为控制点，在每一个原始四边形面片上构造一个双三次Bézier曲面(,)，其中，是参数。

2.2 曲率线网的优化

本文基于Bézier曲面拼接的复合曲面生成的具有规整曲率线网需考虑以下约束。

(1) 曲率线约束。考虑曲面片(,)的一个边界曲线()，并优化其成为曲面的近似曲率线。假设()上的曲面法向量是()，()是曲线()上的切矢量。根据曲面上曲率线的性质可知曲线()是曲面的曲率线，当且仅当曲线()上每一点满足如下约束[14]

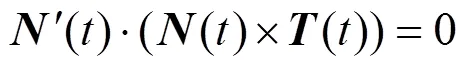
其中，参数可以任意参数化，且()和()不要求是单位向量。在曲线上计算+1个采样点，建立目标函数

定义曲面的曲率线目标函数为

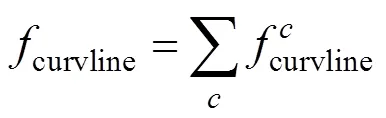
(2) 曲面光滑拼接约束。根据Bézier曲面的几何性质，其拼接的连续性条件可以用公共边界邻近的曲面控制点的关系表示。在设计过程中，由于四边形片面拼接的曲面上不存在奇异点，因此相邻的Bézier曲面1拼接的目标函数比较简单，记为smooth。

(3) 网格光顺控制。为了得到光顺的曲面形状，需增加网格的光顺控制项，即

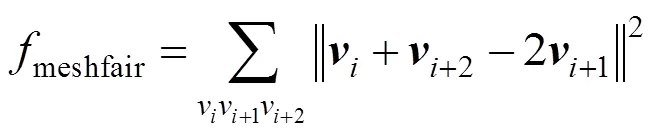
其中，v,v+1,v+2是网格流线上相邻的3个顶点。该函数可使得流线上的顶点趋向均匀分布。

(4) 距离约束。为了避免曲面的形状变化太大，增加网格顶点到初始位置的距离误差，即

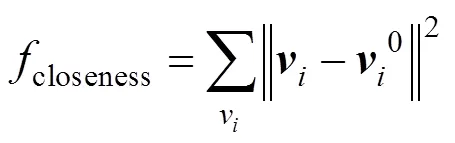
曲面优化目标函数为

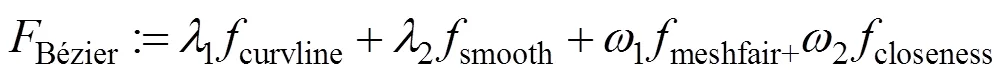
由极小化目标函数式(2)得到具有规整曲率线网的复合Bézier曲面，其优化变量是曲面的所有控制点P。利用Gauss-Newton算法极小化目标函数式(2)，解析出算法中需要的导函数。目标函数中的权重取经验值，本文选取的权重值分别为1=0.1，2=0.1，1=0.001，2=0.100。

2.3 曲面细分

曲率线优化生成由Bézier曲面片拼接构成的曲面，曲面片的边界曲线是近似曲率线。初始控制网格的控制点较少，无法生成形状复杂的曲面，本文通过曲面细分并增加曲面控制点的数量，从而增加造型的自由度。在建筑曲面设计中，曲面片的大小与建筑的结构性质和制造成本有紧密联系，因此对曲面片的大小有具体的要求。在设计过程中，若曲面片大小不符合要求时，需进一步细分。

细分操作需将1个Bézier曲面剖分成4个，可通过重新参数化实现，细分的结果不改变曲面的形状。当继续优化曲率线时，在曲面光顺项的作用下，曲面的形状变得更加光顺，同时该边界曲线就是曲面的曲率线。

曲率线优化和曲面细分需要交替执行，可生成具有足够数目曲面片的光滑曲面。设计人员的设计意图决定了最终生成的曲面的面片数目，以此确定曲率线优化和曲面细分交替执行的次数。结果得到1拼接的Bézier曲面片构成的自由形状，曲面片的边界曲线可生成曲面的曲率线网。

2.4 生成圆纹样条曲面

为得到圆纹曲面片光滑拼接的曲面，在每一片Bézier曲面的位置构造一个圆纹曲面片，其生成的复合曲面上曲面片的边界曲线是曲率线。得到的曲面形状符合设计要求时，进行圆纹曲面优化，当曲面的控制网格符合圆纹样条曲面的约束，可确定一个圆纹样条曲面。

不管注册会计师怎样小心严谨与认真，审计风险都是无法避免的。追其根本因素，审计风险是属于客观性的存在，列入审计成本方面的因素，想要减少审计风险就需要投入很大的人力与物力的资源，当风险被减少到一定程度的时候，进一步减少审计风险会造成适得其反。

因为曲率线优化和曲面细分算法生成的光滑Bézier曲面的边界曲线是近似曲率线，为圆纹样条曲面优化提供了高质量的初始。由Bézier曲面的控制网格顶点得到圆纹样条曲面，其形状和曲率线优化和曲面细分算法得到的Bézier复合曲面相比改变微小。基于Bézier曲面表示的圆纹曲面优化的约束如下：

圆纹曲面要求曲面边界端点标架满足该约束。考虑图4中的曲面边界0003，约束条件为

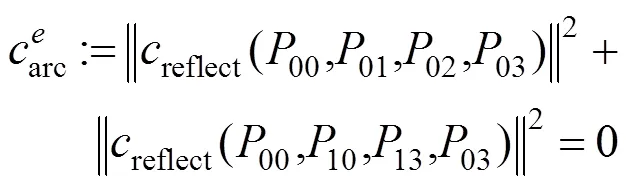
圆纹曲面优化的反射目标函数为

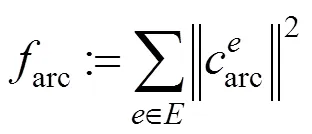
该目标函数的求和针对所有的网格边。

(2) 切向垂直约束。以图4中曲面片的顶点00为例，切向垂直约束为

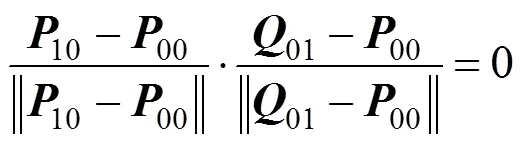
正交约束的目标函数是

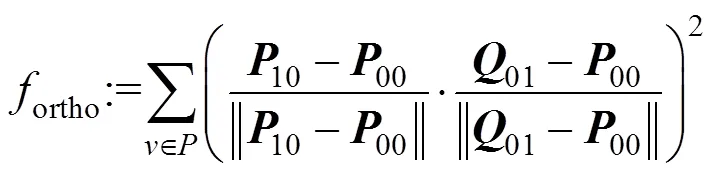
(3)1拼接约束。要求相邻曲面片的边界曲线光滑拼接，且相关控制点在一条直线上。图4中2个曲面片在00点的1拼接条件为

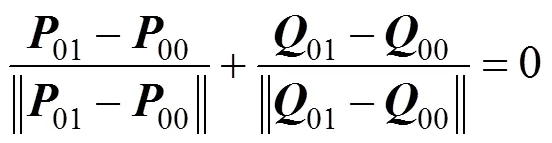
即曲面光滑拼接目标函数为

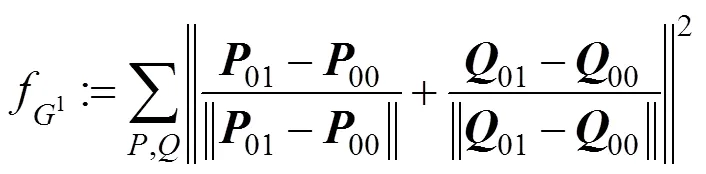
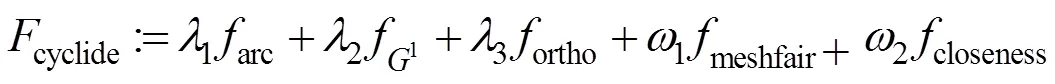
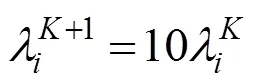
2.5 复合曲面分析

本文计算一个具有规整曲率线网的由Bézier曲面1拼接的复合曲面。基于该曲面可得到圆纹样条曲面优化的非常好的初始几何信息，并提供了对最后生成的圆纹样条曲面形状的视觉评估依据。

根据圆纹曲面的定义以及曲面主曲率线网的几何性质可知：曲率线优化和曲面细分的迭代算法构造的Bézier曲面的控制网格如果满足约束条件(3)，控制网格可以确定一个圆纹曲面片。网格光顺可使控制点形成对称性，但即使满足条件(3)，双三次Bézier曲面仍无法精确表示圆纹曲面。所以希望算法生成的Bézier曲面以较高的精度近似一个圆纹样条曲面，且对双三次Bézier曲面逼近圆纹曲面片的能力感兴趣。

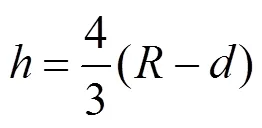
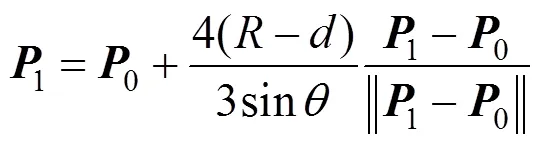
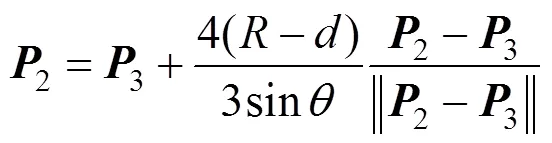
记梯形控制多边形生成的Bézier曲线上点的坐标(,)，圆弧对应点的坐标(，)。用|－|表示2条曲线的误差，记夹角对应的Bézier曲线和圆弧之间的最大误差为()。

举例说明误差()随角度的变化。给出一个控制多边形，控制点坐标0=(–10，0)，3=(10，0)，1和2由式(8)和式(9)计算得到。计算该曲线上采样点的(平均分成100份)最大误差()，如图5所示。实验表明，随减小最大误差()逐渐减小，当=89°时曲线上采样点的最大误差是0.313 1；当=30°时，曲线的最大误差是0.021 7。图6给出=89°和=30°时的圆弧和三次Bézier曲线。在圆纹样条曲面上的圆弧角度一般不大，因此控制点满足圆纹曲面约束的Bézier曲面与圆纹曲面片的逼近程度较高。

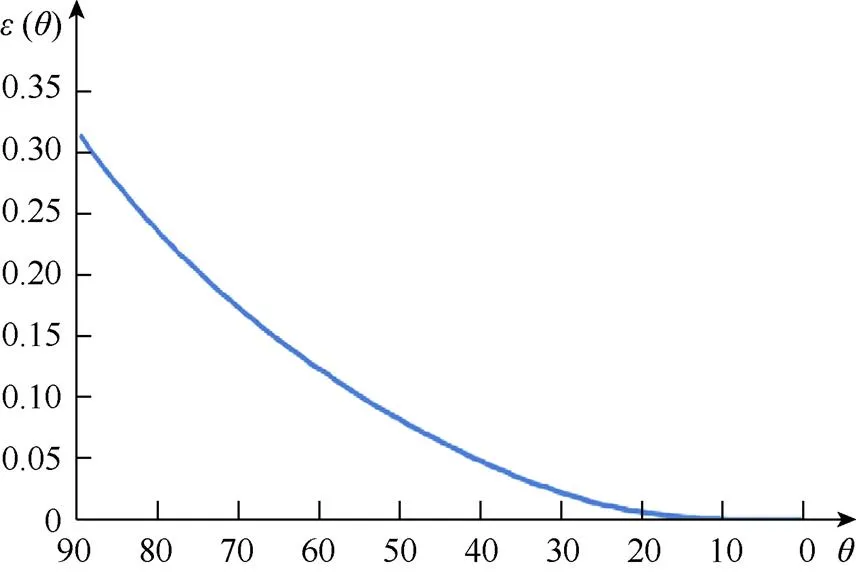
图5 圆弧和Bézier曲线的最大误差

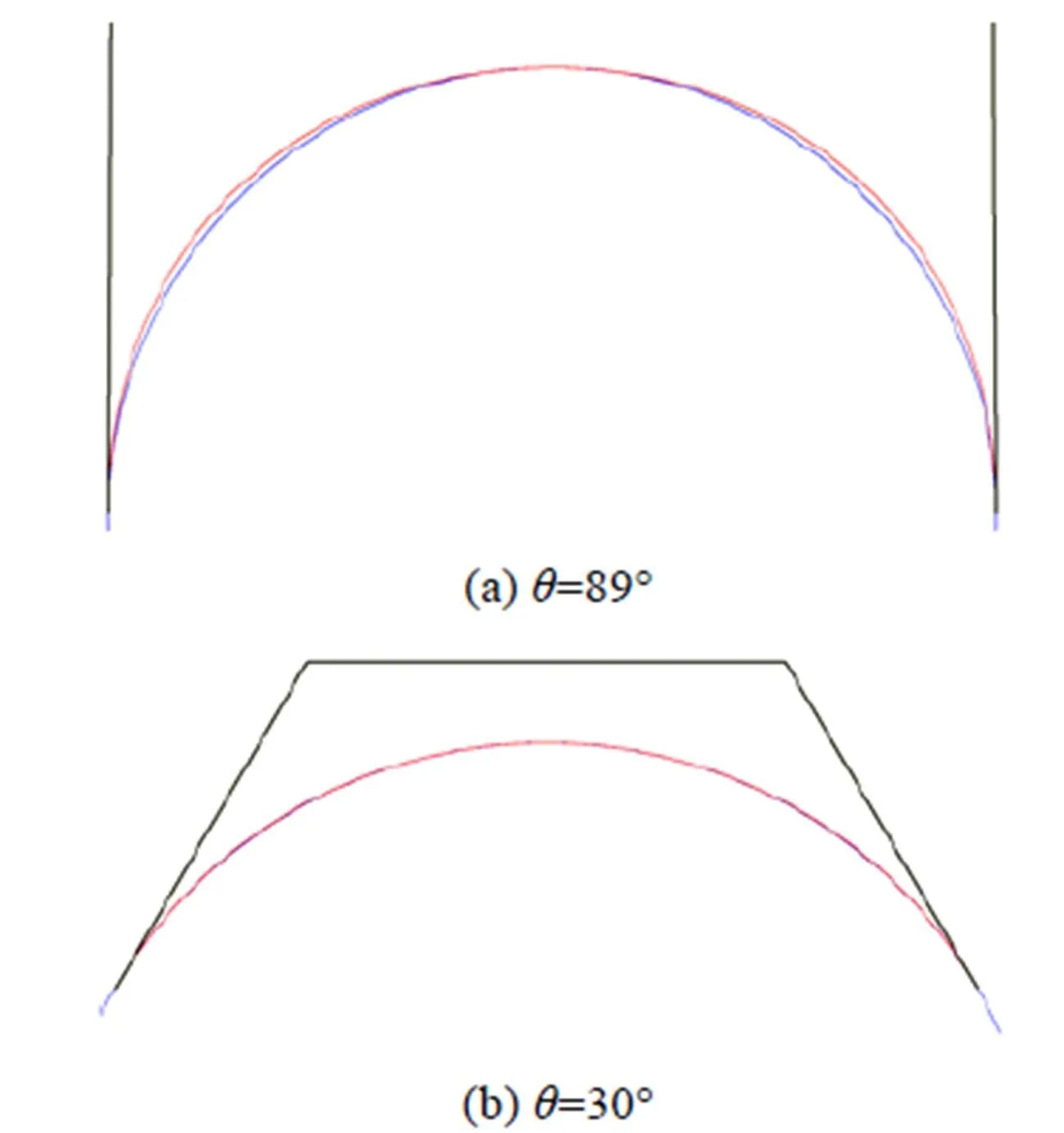
图6 圆弧和Bézier曲线的形状

由于圆纹曲面片由正交的圆弧构成，因此三次Bézier曲线表示圆弧的能力与双三次Bézier曲面表达圆纹曲面片的能力有密切关系，但从理论论证双三次Bézier曲面表达圆纹曲面片的能力的相关结论比较困难。虽然利用有理Bézier曲面能够精确表示曲面的边界圆弧，但是基于有理形式的目标函数的优化要更困难，而且本文使用双三次Bézier曲面只是作为一种中间表示形式，不要求能够精确表示圆弧。

3 实验和讨论

3.1 曲率线准确度的可视化

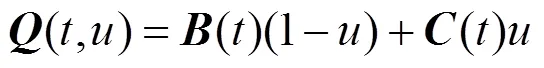
3.2 实例和讨论

(1) 圆纹样条曲面建模实验。图7~10给出了几个模型的设计和优化过程，以及生成的圆纹样条曲面。图(a)为交互设计的初始网格；图(c)~(h)展示了优化和细分迭代过程中的中间结果，并显示了衡量曲率线精确度的颜色编码，其中，图(c)和图(d)分别为优化前、后的曲面以及曲面上的曲率线可视化；图(e)和图(f)经过1次曲面细分后，优化前、后的曲面以及曲率线可视化；图(g)和图(h)经过再一次细分后，优化前、后的曲面以及曲率线可视化。基于最后得到的具有规整曲率线网格结构的曲面，通过圆纹样条曲面优化得到圆纹样条曲面(图(b))。实验说明本文方法能够有效地设计具有规整结构的自由形状的圆纹样条曲面。

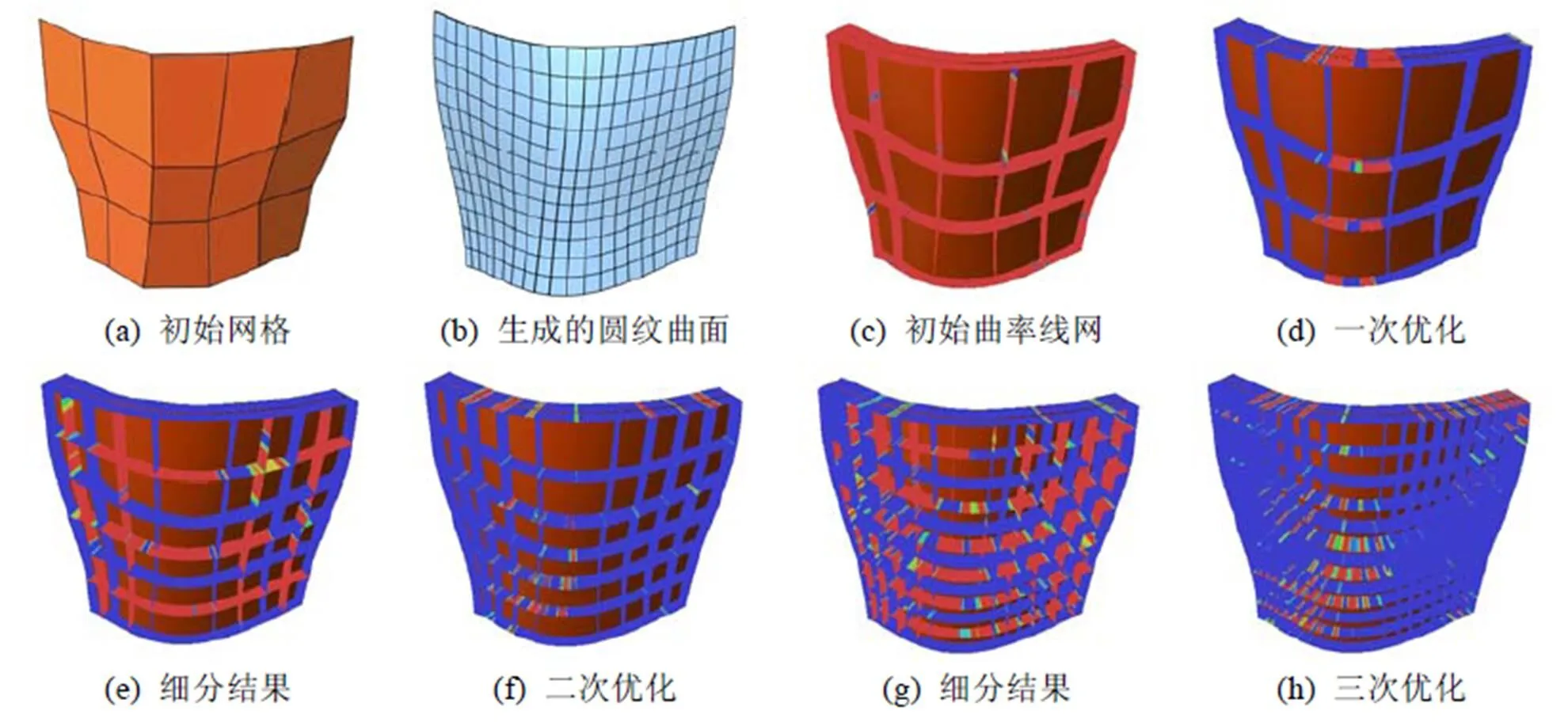
图7 模型1规则的优化过程

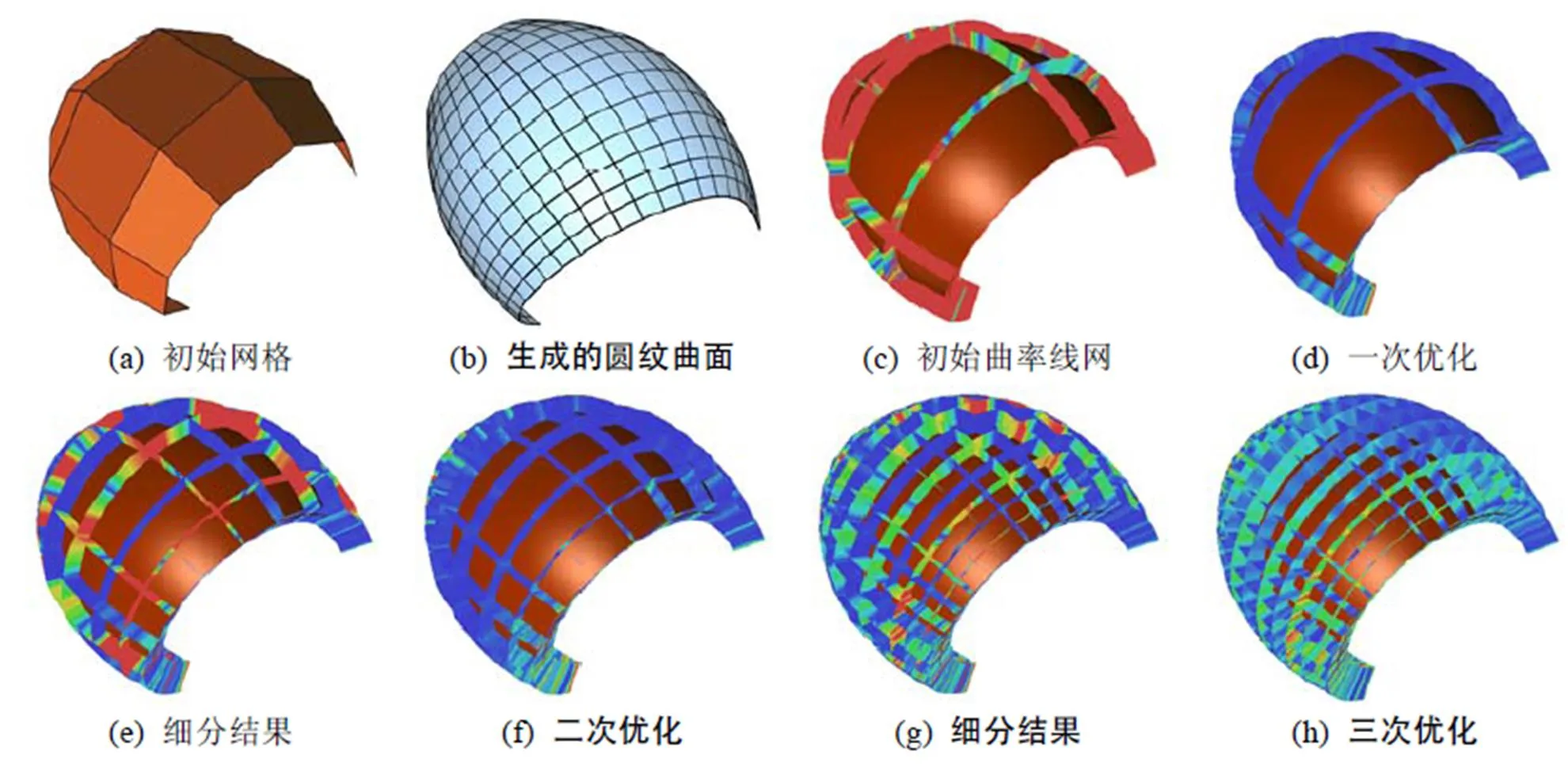
图8 模型2的优化过程

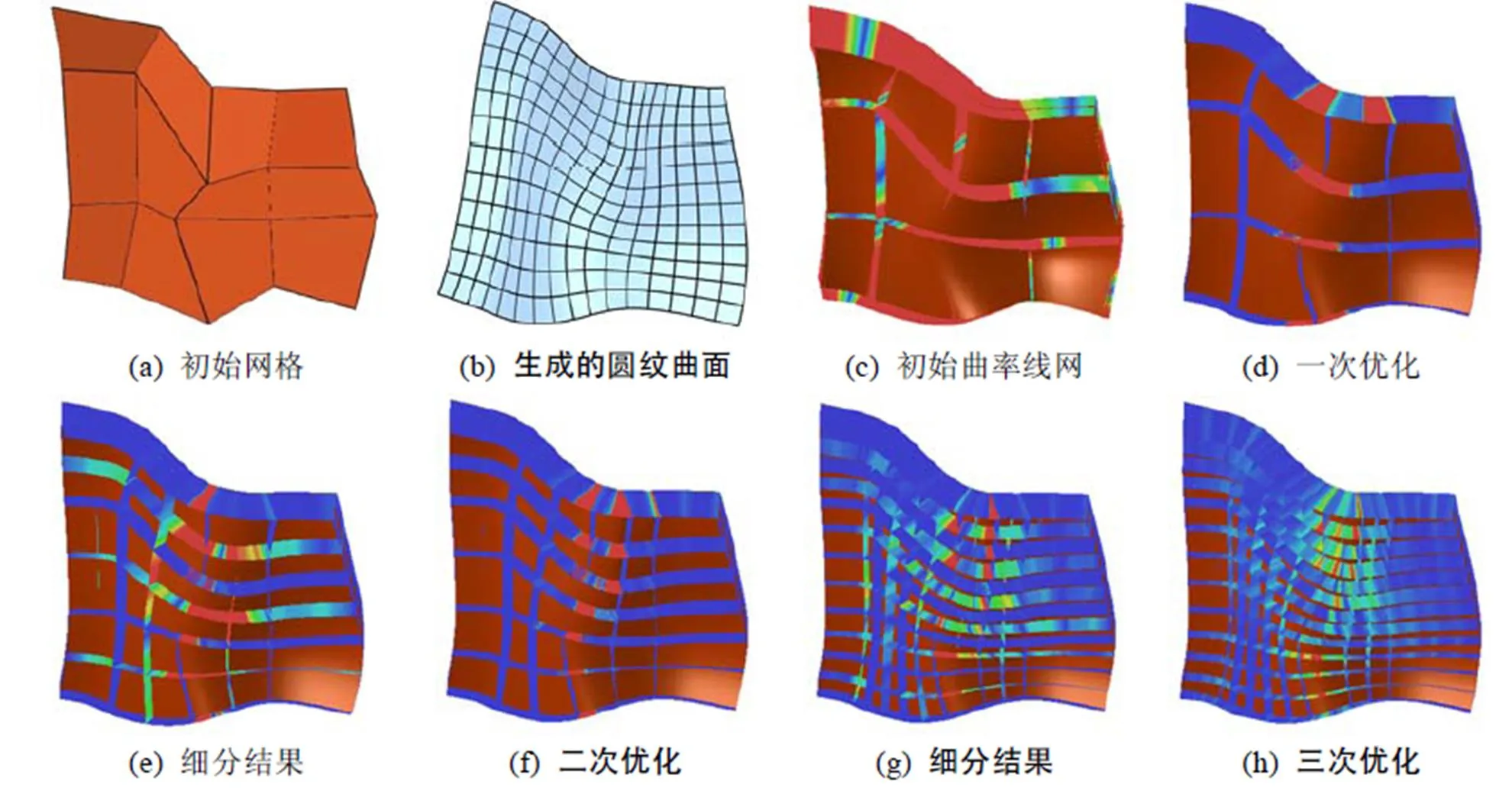
图9 模型3的优化过程

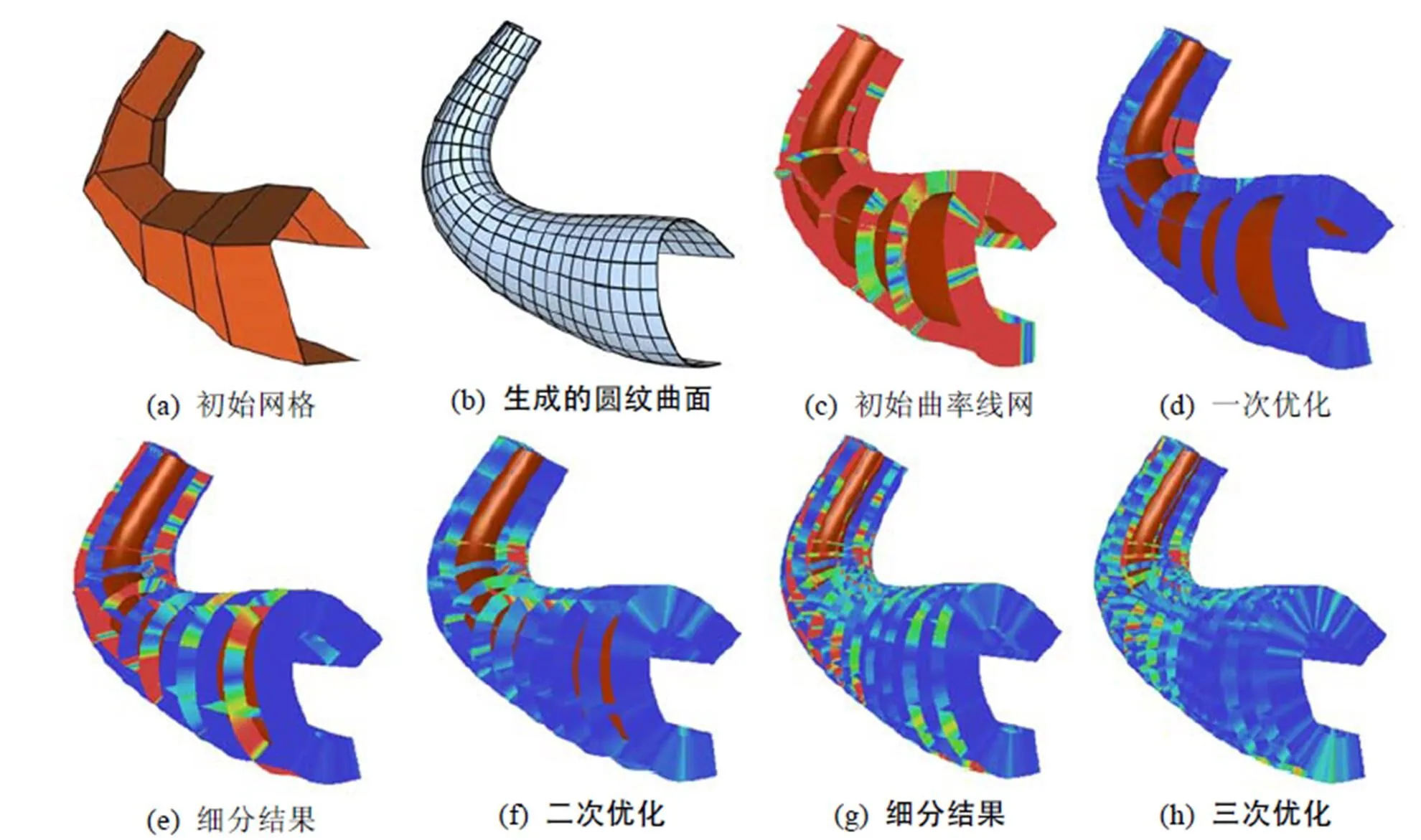
图10 模型4的优化过程

图中显示了优化曲面设计过程中曲面边界上沿法向的垂直曲面的可展性颜色编码，反映曲面边界是曲面的曲率线的程度。曲率线优化结束条件由式(10)计算的平均误差决定，其可达到10–4数量级，如图10中的模型曲面片边界曲线上的直纹面的可展性式(10)的平均值为1.5×10–4。以此结果作为初始，利用优化算法可以成功得到具有规整曲率线网的圆纹样条曲面。本实验的测试平台为Intel Core i5 2.5 G CPU，4 G内存，1T 硬盘的笔记本电脑。图7~10的优化时间分别为：6 s，7 s，7 s和10 s。

(2) 自由曲面建筑结构的生成。图11、12给出几个圆纹样条曲面的结果及特殊几何结构。图11和图12(a)给出了圆纹样条曲面的等距面，根据圆纹曲面的几何性质，一个圆纹样条曲面的等距面也是一个圆纹样条曲面。图11和图12(b)~(c)给出了由圆纹样条曲面得到的沿2个不同方向的圆锥条模型(conical strip)，在基于单向弯曲的可展曲面条的建筑表面设计和建造中有重要应用[16]。

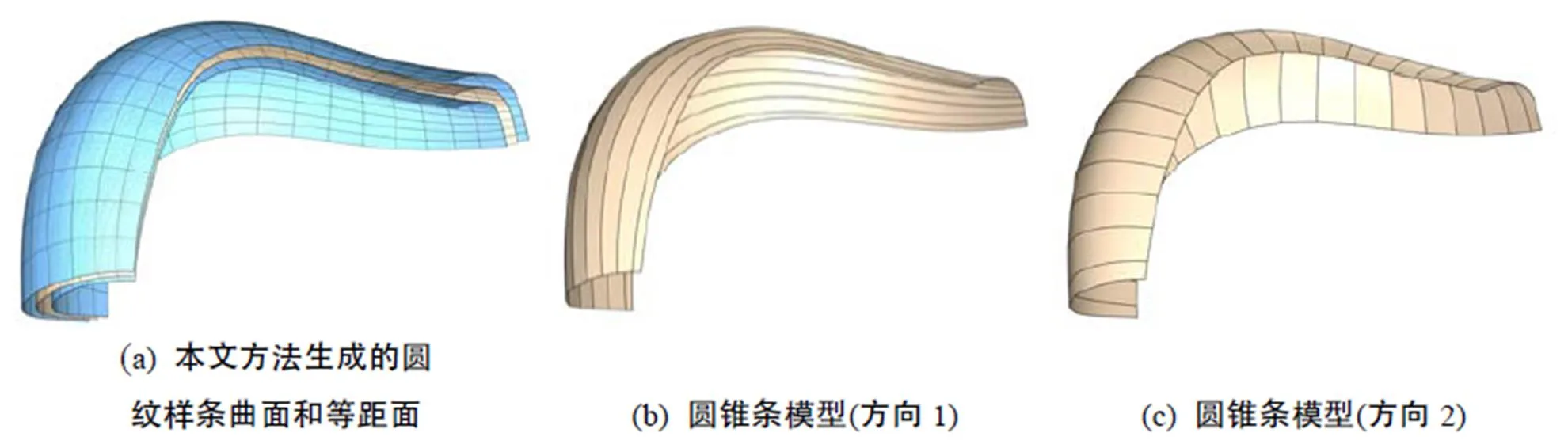
图11 圆纹样条曲面结果及上面的几何结构(模型5)

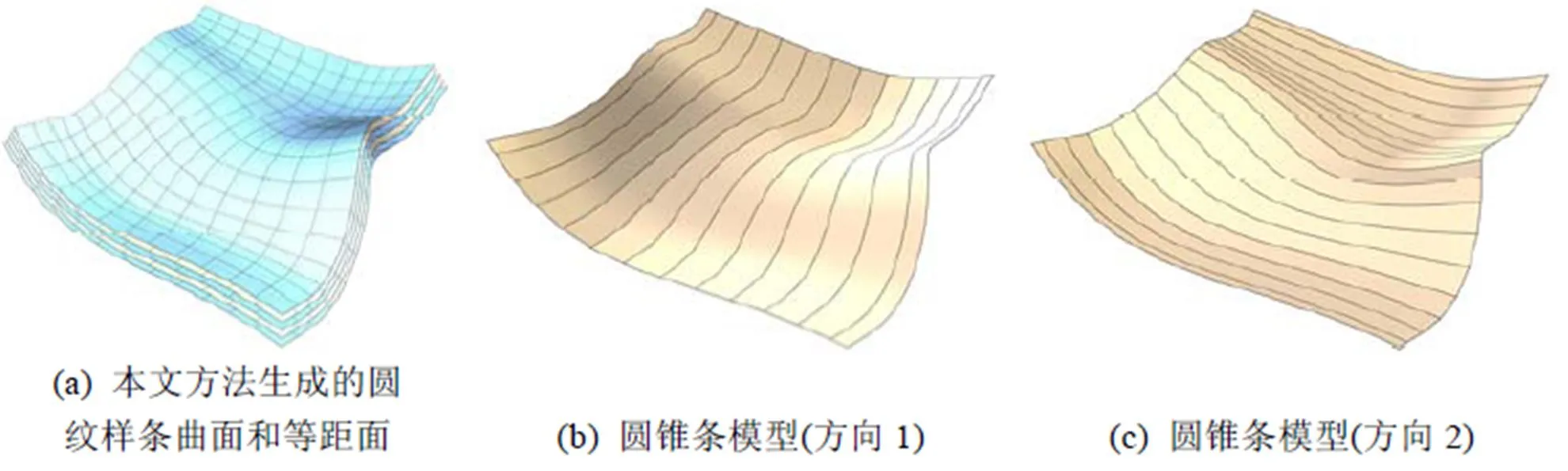
图12 圆纹样条曲面结果及上面的几何结构(模型3)

在建筑设计中，其表面的支撑结构是曲面垂直的可展曲面，且曲面只能沿着曲面的主曲率线构造[17]。本文得到的曲率线规整的光滑曲面上的可展曲面(,)就是建筑设计中的支撑结构。图13给出了结果曲面上的垂直支撑结构。

4 结束语

本文提出一种曲面的设计算法，能够生成具有规整曲率线网而且无脐点的光滑曲面。基于该方法，结合圆纹样条曲面的优化，能够得到具有规整结构的圆纹样条曲面，以及多种在自由建筑曲面设计中具有重要应用的特殊几何结构。

未来的工作包括研究算法效率的提高以及曲面的交互形状调整和编辑，目标是找到一种具有规整曲率线网的自由曲面交互设计技术。另外基于具有规整曲率线网的曲面的数控加工刀具形状和运动轨迹的计算也有重要意义，是未来的研究方向。

[1] LIU Y, POTTMANN H, WALLNER J, et al. Geometric modeling with conical meshes and developable surfaces [J]. ACM Transactions on Graphics, 2006, 25(3): 681-689.

[2] NICHOLAS M P, TAKASHI M. 计算机辅助设计与制造中的外形分析[M]. 冯结青, 叶修梓, 译. 北京: 机械工业出版社, 2005: 20-30.

[3] POLIAKOFF J F. An improved algorithm for automatic fairing of non-uniform parametric cubic splines [J]. Computer-Aided Design, 1996, 28(1): 59-66.

[4] JOSHI P P. Minimizing curvature variation for aesthetic surface design [M]. Berkeley: University of California at Berkeley, 2008: 1-10.

[5] ZHANG C M, ZHANG P F, CHENG F H. Fairing spline curves and surfaces by minimizing energy [J]. Computer-Aided Design, 2001, 33(13): 913-923.

[6] YONG J H, DENG B L, CHENG F H, et al. Removing local irregularities of triangular meshes with highlight line models [J]. Science China Information Sciences, 2009, 52(3): 418-430.

[7] 张跟全, 张彩明. 基于高光线模型修改NURBS曲面不光顺性[J]. 计算机辅助设计与图形学学报, 2003, 15(5): 561-565.

[8] ALLIZE P, COHEN-STEINER D, DEVILLERS O, et al. Anisotropic polygonal remeshing [J]. ACM Transaction on Graphics, 2003, 22(3): 485-493.

[9] KNÖPPEL F, CRANE K, PINKALL U, et al. Globally optimal direction fields [J]. ACM Transaction on Graphics, 2013, 32(4): 59:1-59:10.

[10] PAN H, LIU Y, SHEFFER A, et al. Flow aligned surfacing of curve networks [J]. ACM Transactions on Graphics, 2015, 34(4): 127.

[11] BO P B, LIU Y, TU C H, et al. Surface fitting with cyclide splines [J]. Computer Aided Geometric Design, 2016, 43c: 2-15.

[12] MARTIN R R. Principal patches: A new class of surface patch based on differential geometry [C]// Eurographics’83. Goslar: Eurographics Association Press, 1983: 47-55.

[13] SRINIVAS Y L, KUMAR V, DUTTA D. Surface design using cyclide patches [J]. Computer-Aided Design, 1996, 28 (4): 263-276.

[14] 郑荟莹, 伯彭波. 曲率线驱动的B样条曲面交互编辑[J]. 计算机辅助设计与图形学学报, 2018, 30(6): 1065-1072.

[15] DO CARMO M P. Differential geometry of curves and surfaces [M]. Upper Saddle River: Prentice-Hall Inc, 1976: 112-113.

[16] POTTMANN H, SCHIFNER A, BO P B, et al. Freeform surfaces from single curved panels [C]//ACM Transactions on Graphics, SIGGRAPH’08. New York: ACM Press, 2008: 76.

[17] TANG C C, KILAN M, BO P B, et al. Analysis and design of curved support structures [C]//Advances in Architectural Geometry 2016. Cham: Springer Intemational Publishing, 2016: 8-23.

Design of Smooth Surfaces with Regular Network of Curvature Curves

ZHENG Hui-ying, BO Peng-bo

(School of Computer Science and Technology, Harbin Institute of Technology (Weihai), Weihai Shandong 264209, China)

A new algorithm is proposed for the design of a smooth surfaces which is required to have a regular mesh of curvature curves without any umbilical points. A composite surface as smoothly joint by Bézier surface patches is used in the design procedure. By the alternative steps of optimization of curvature line networks and surface subdivision, the free from surface is generated which has a regular network of curvature curves without an umbilical point. Based on the resultant surface, a cyclide spline surface with regular structures, conical strip models and multi-layer support structures for freeform architectural surface design are easily obtained.

curvature line network; cyclide surface; umbilical point; surface design

TP 391

10.11996/JG.j.2095-302X.2019010046

A

2095-302X(2019)01-0046-08

2018-06-06；

2018-06-24

国家自然科学基金项目(61672187)；山东省重点研发计划项目(2018GGX103038)；模式识别国家重点实验室开放课题项目(201800013)

郑荟莹(1993-)，女，河南周口人，硕士研究生。主要研究方向为计算机辅助几何设计。E-mail：pengbo@hitwh.edu.cn

伯彭波(1978-)，男，山东威海人，副教授，博士，硕士生导师。主要研究方向为计算机图形学。E-mail：pbbo@hit.edu.cn