高斯过程回归方法在浙江沿海海岛冬春季阵风预报中的应用试验

胡波，俞燎霓，滕代高

(浙江省气象台，浙江 杭州310017)

1 引 言

浙江沿海港口众多，经贸发达，海岛旅游资源丰富，海上大风易造成突发灾害，因此研究近地层风场的阵风特征、风速切变和空间结构等对提高预报准确率，保障航运安全、建筑抗风设计等有重要意义[1-3]。阵风成因复杂，普遍认为与大尺度风、湍流和大气稳定度等有关，气流的水平动量传输及对流拖拽导致的垂直动量传输均扮演了重要角色[4-8]，可见阵风的影响因子复杂，其预报必然存在不确定性[9-10]，为此将预报从单一值的确定论向多值的概率论转变符合气象科学，它能够把预报的不确定性定量化并事先告知广大用户，不同的用户就能根据自身对气象条件的依赖程度做出不同的决策以达到最好的经济和社会效益[11-14]。

目前概率预报已经成为国内外研究的重要领域之一[15-19]。国内主要利用数值预报产品，通过统计方法建立概率预报模型，研究的重点领域为降水预报，如马培迎[20]、陈朝平等[21]利用贝叶斯公式求得暴雨的后验分布，并建立了暴雨预警模型；邵明轩等[22]利用非线性多因子动态组合方法进行降水概率预报；李明[23]通过计算优选的对流参数值，结合参数历史概率分布值及其权重，建立分月短时强降水客观概率预报模型；姜丽黎等[24]采用动力与统计相结合的方法，对台风引起的极端降水事件进行概率预报方法的研究。这些降水概率预报比起确定性的预报更能满足交通、航空、农业、水利和电力等部门的不同需求，提高了天气预报的使用效益。国内利用概率方法预报阵风的研究较少，国外已有许多学者进行了研究，如Sloughter 等[25]采用贝叶斯模型平均法（MBA）将预报风速作为混合的Gamma 分布来实现概率预报，Lerch 等[26]采用非齐次回归法预报德国的日大风。Thorarinsdottir等[27]则基于风速服从高斯分布的假设，采用高斯回归法实现大风概率预报。

从技术路线来看，目前概率预报方法分为两类，第一类是利用数值模式（集合预报）计算出事件发生的概率；第二类是利用模式产品结合实测资料，采用统计方法制作概率预报。第一类方法基于集合预报的动力数值模式，需大量人力物力支持，在省级气象台站开展存在许多困难；第二类方法本质为模式产品本地化解释应用，为省级气象台站研究重点方向，本研究采用第二类概率预报方法。

2 数据和方法

2.1 数 据

地面风场观测资料来自浙江海岛的4 个气象观测站，从南到北覆盖整个浙江沿海，分别为嵊泗（58472）、东 矶（58663）、大 陈 岛（58666）、南 麂（58764），具体地理位置见图1。资料时间跨度为2006—2016年的12—3月，大风资料包括10 min的平均风速和期间所对应的极大风速，如极大风速出现在05:08，则取05:01—05:10 的10 min 平均风速。

大气环流数据来自http://apps.ecmwf.int/datasets/网站，采用ERA-interim 一天四时次（北京时分别为02、08、14 和20 时）的高度、温度、风速、比湿、涡度、散度等要素数据，时间跨度为2006—2016年，水平分辨率为0.125°×0.125°，垂直层包括10m、1 000 hPa、975 hPa、950 hPa、925 hPa、900 hPa、875 hPa、850 hPa、825 hPa、800 hPa、775 hPa、700 hPa、650hPa、600hPa、550hPa、500hPa。

本文重点对沿海大风进行研究，选取的样本中10m平均风速≥8.0m/s，共选取整点样本4 975组。

2.2 阵风数据特征

阵风因子是阵风特征的重要参数，世界气象组织(WMO)给出其定义为在时距T0的时间段内持续时间为τ 的最大风速与时距为T0的平均风速之比，即[28]：

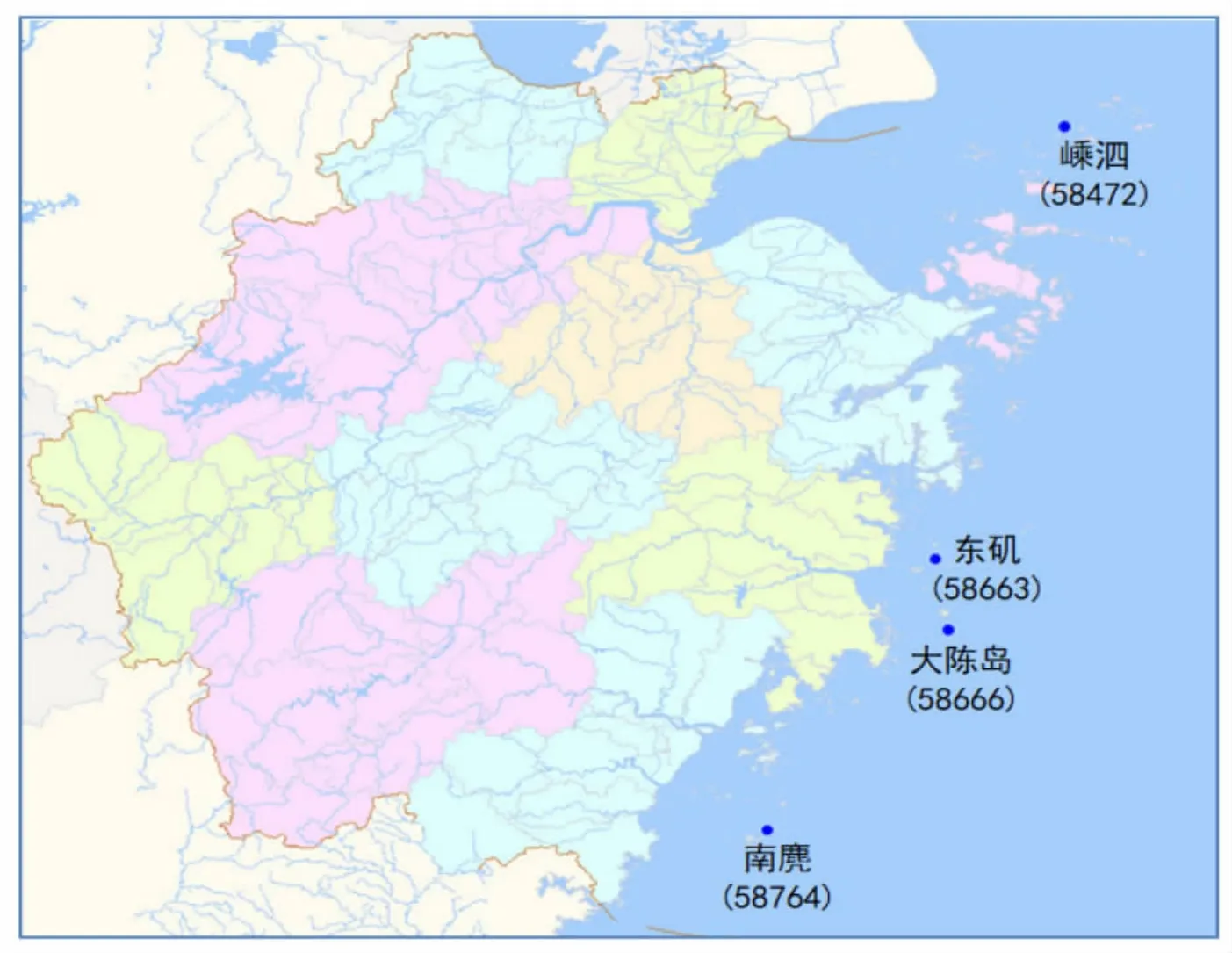
图1 四个海岛气象测站的地理位置

式中，Vτ，T0为观测周期T0中持续时间τ 的风速最大值(阵风)，VT0为观测周期T0的风速平均值。阵风因子计算时，T0必须大于3 min 才具有代表性，本文取T0为10 min，τ 为3 s。

图2 为四个海岛站10 min 平均风速和阵风因子的对应关系。从总体上来看，四个站阵风因子在平均风速较小时波动幅度要大一些，如平均风速在8.0～10.0m/s 时，嵊泗站和大陈岛站阵风因子上下界波动范围在1.15～1.80 之间，而东矶站和南麂站上界要大一些，其上下波动范围为1.1～2.0之间。随着平均风速增加，各站阵风因子的波动范围逐渐减少，相对来说，东矶站和南麂站上边界减小的速度更快些，在平均风速为16m/s，其上边界约为1.3～1.4，而另外两个站约为1.5～1.6，四个站下边界变化基本一致，均随着平均风速增大基本保持不变。从样本出现概率较高区域（黄、红色区域）的分布来看，嵊泗站、大陈岛站阵风因子波动范围为1.2～1.5，另外两站则为1.1～1.3。可见，在相同平均风速情况下，阵风因子可以有较大变化，导致对应的阵风也出现大的差异，譬如平均风速在10m/s 时，嵊泗站对应的阵风可以为11m/s，也可以高达19m/s，变化范围大，而东矶站由于阵风因子波动幅度更大，对应阵风上界甚至可达22m/s，说明阵风数据分布具有混沌性，业务中准确定量预报存在困难，因此采用概率预报方法具有实际意义。

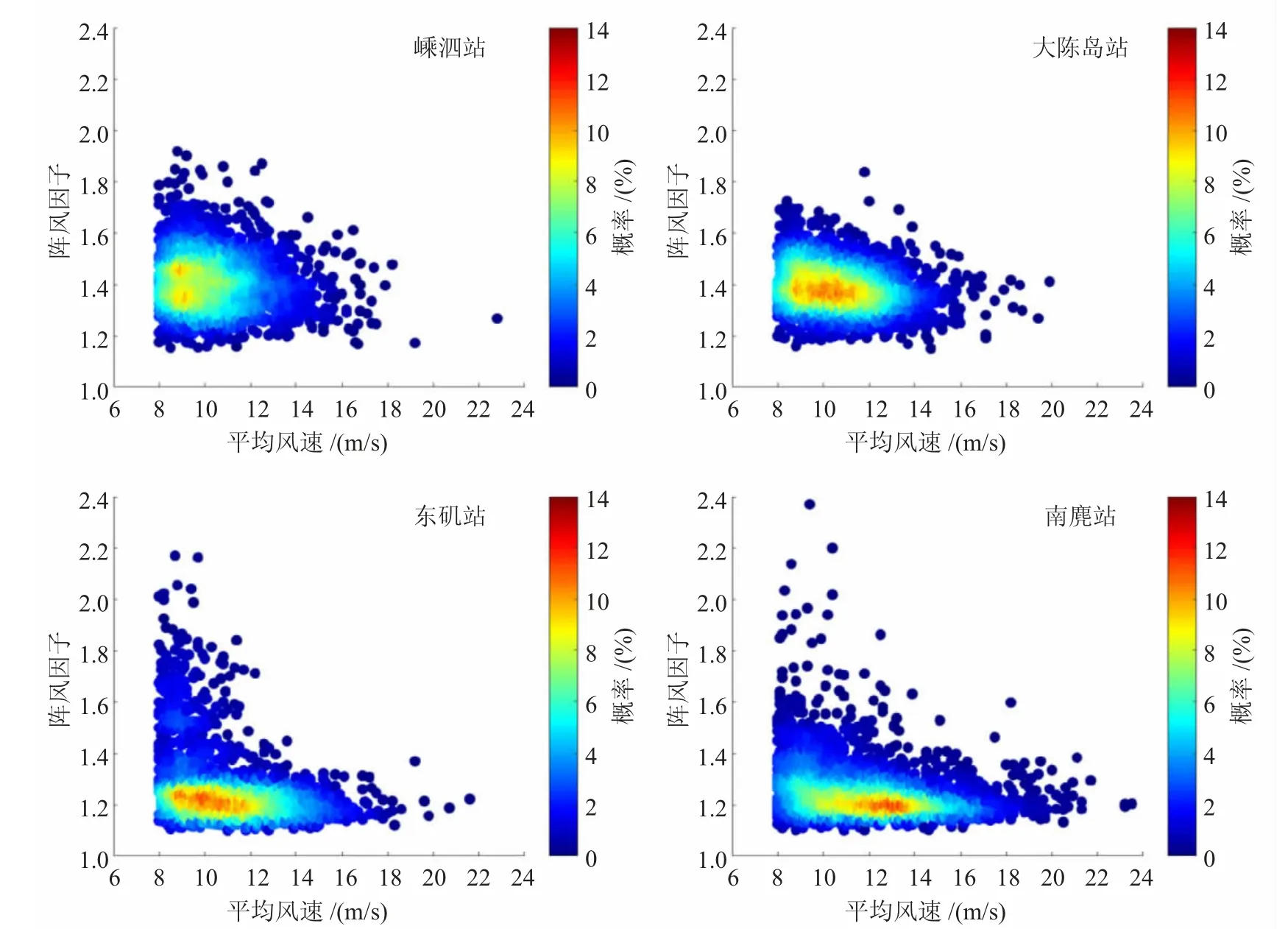
图2 四个海岛站冬春季大风的10 min 平均风速与对应阵风因子的关系颜色代表样本出现概率，概率按照平均风速2.0m/s 和阵风因子0.06 的间隔进行计算。

为了选择合适的概率预报方法，需要知道阵风样本的先验概率分布。 首先利用Kolmogorov-Smirnov 方法对四个站的阵风样本进行正态分布检验，结果表明嵊泗站和南麂站样本为准正态分布，而东矶站和大陈岛站符合正态分布，为了让阵风样本进一步接近正态分布，将阵风进行自然对数处理[29]后，检验表明四个站阵风数据均已符合正态分布，通过了0.01 显著性水平检验。图3 为不同阵风风速样本对应的概率密度估计，左边为10m阵风的概率密度估计，右边为10m阵风自然对数的概率密度估计。可见，嵊泗站阵风在自然对数处理后，其概率分布明显与正态分布（棕色线）更加符合，南麂站则在自然对数处理后，数据在小值和大值时的概率分布更加对称，符合正态分布（棕色线）。图4 为四个站样本的Kolmogorov-Smirnov 正态分布检验的概率累积分布，与标准化阵风样本比较，四个站点阵风样本在自然对数处理后，其经验概率累积分布和标准正态的经验概率累积分布曲线更加重合。

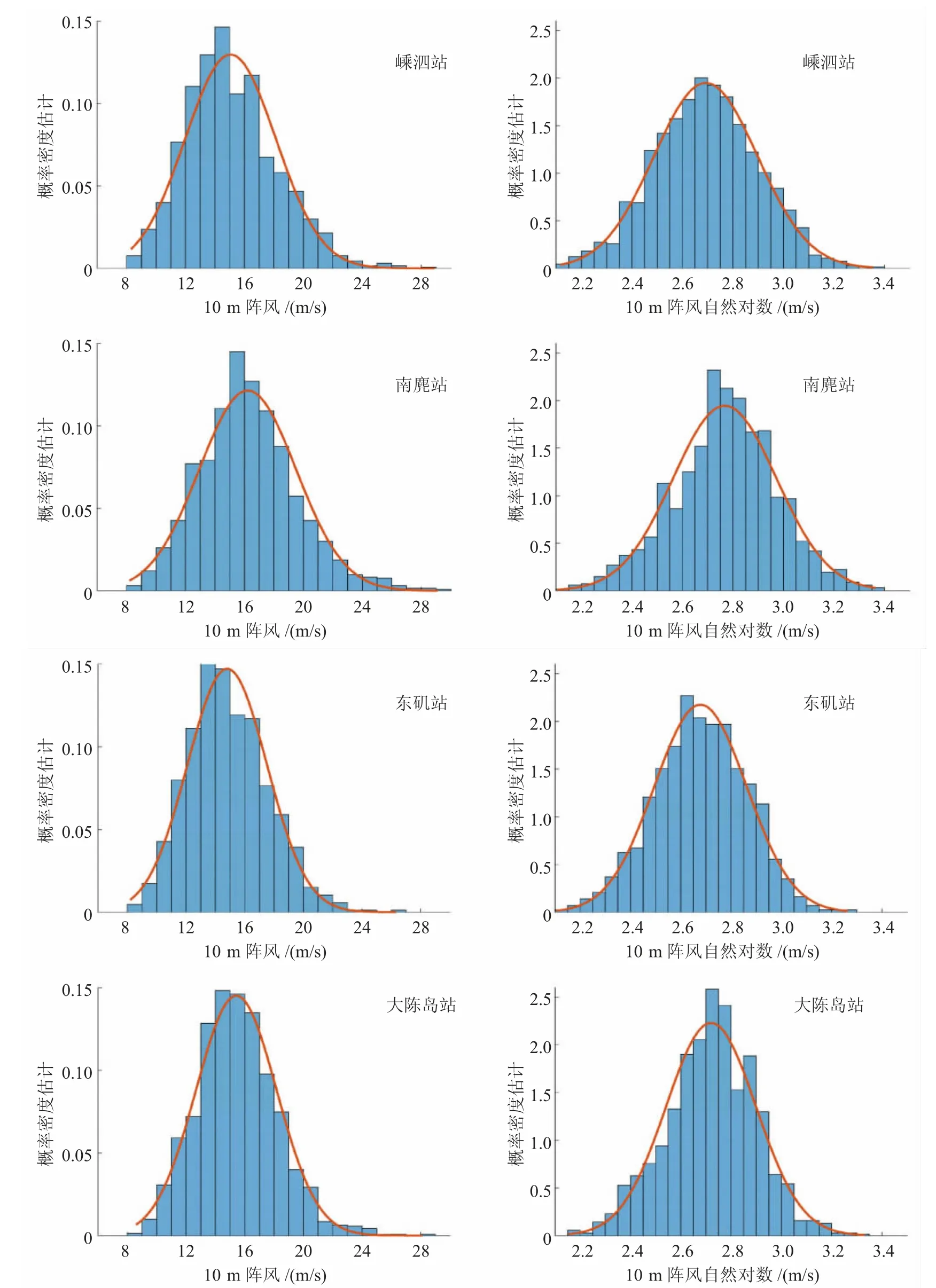
图3 不同阵风风速样本对应的概率密度估计 棕色线为标准正态分布曲线。左边为10m阵风样本，右边为10m阵风自然对数样本。

高斯过程回归是基于贝叶斯理论和统计学习理论发展起来的一种全新机器学习方法，它作为一种贝叶斯非参数模型[30-32]，可以自动适应自身接受到的数据，事先不用指定模型大小和参数个数，具灵活性高、性能稳健的优点，在各行业中得到广泛应用[29,33]。在气象领域，Lerch 等[27]将高斯过程回归与贝叶斯模型平均法（MBA）的预报结果进行比较，结果显示这两种方法的预报性能接近，而Feldman 等[34]则在概率预报研究中进一步指出高斯回归方法相对于MBA 方法，其概念更加简单，计算更加有效。由于沿海阵风数据具正态分布（高斯分布）的特征，其概率预报模型采用高斯过程回归方法是适宜的。

2.3 高斯过程回归方法介绍[28]

2.3.1 高斯过程回归原理

从函数空间角度出发，定义一个高斯过程(GP)来描述函数分布，直接在函数空间进行贝叶斯推理。GP 是任意有限个随机变量均具有联合高斯分布的集合，其性质完全由均值函数和协方差函数确定，即：

其中，x，x'∈Rd为任意随机变量，因此GP 可定义为f(x)～GP(m(x)，k(x, x' ))。为了符号上的简洁，通常对数据作预处理，使其均值函数等于0。

对于回归问题，考虑如下模型：

其中：x 为输入向量，f 为函数值，y 为受噪声污染的观测值，进一步假设噪声。可以得到观测值y 的先验分布为：

以及观测值y 和预测值f*的联合先验分布为：

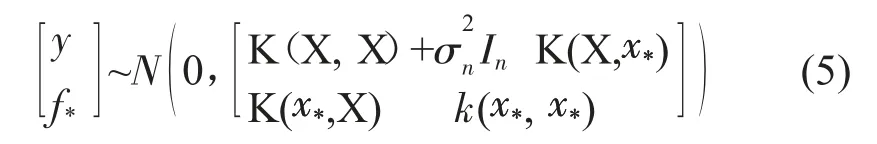
其中：K(X, X)=Kn=(kij)为n×n 阶对称正定的协方差矩阵，矩阵元素kij=k(xi, xj)用来度量xi和xj之间的相关性；K(X, x*)=K(x*, X)T为测试点x*与训练集的输入值X 之间的n×1 阶协方差矩阵；k (x*,x*)为测试点x*自身的协方差，In为n 维单位矩阵。

由此可以计算出预测值f*的后验分布为：

其中：

高斯过程回归可以选择不同协方差函数，常用的有平方指数协方差，即：

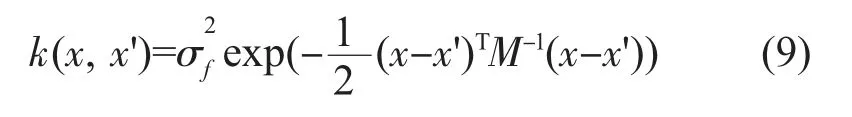
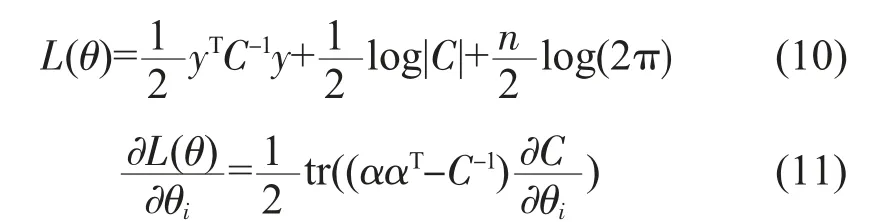
2.3.2 高斯过程回归的主要优缺点

高斯过程回归方法具有容易实现、灵活的非参数推断、超参数自适应获取等优点，是一个具有概率意义的核学习机，它不仅能够对未知的输入进行预测输出，而且能够对该预测输出的精度参数或不确定性进行定量分析；能以先验概率的形式表示过程的先验知识，并通过标准的贝叶斯方法进行模型选择，从而提高了过程模型的性能；与神经网络和支持向量机等机器学习方法相比，其模型参数明显减少，且能方便推断出超参数。

高斯过程回归方法虽然有许多优点，但也仍在一些问题，主要有两方面，一是计算量大，高斯过程回归非参数性质直接导致其计算量大的问题，训练中超参数一般是通过最优化边缘似然获取的，每一次梯度计算均需要对协方差矩阵求逆，当处理大数据集时，计算量将成为限制其应用的一个瓶颈。二是局限于高斯噪音分布假设，高斯过程回归需要满足噪声符合高斯分布，即观测数据满足多变量联合高斯分布，该假设使得矩阵运算变得简单方便，其预测分布也满足高斯分布，但许多实际情况并不满足这个假设，如观测值为正且在好几个数量级之间变化时，这种情况难以直接假设一个同方差的高斯噪音，这种情况需要先对观测空间数据进行一次或连续数次的变换，然后假设变换后的数据受高斯噪音的污染，此时高斯过程回归方法能得到较好的效果。

3 阵风影响因子分析

为了实现良好的预报效果，需针对性查找与阵风有密切关系的影响因子。由于Brasseur[7]研究认为阵风是由湍流涡旋引发边界层上层气流向近地面的偏移所导致，其主要原理考虑平均湍流涡旋动能大于大气浮力能，具体公式为：

式中的左边项为平均湍流涡旋动能，右边项为浮力能，θv(z)是虚位温，Δθv(z)为某个层次虚位温的变化，本文计算了中层500 hPa 以下至1 000 hPa 的浮力能。

对阵风与不同层次不同大气要素分别进行相关分析，初步选取四个站检验p 值均值≤0.05 的31 个要素为模型准因子（表1），从不同层次高相关因子数目来看，900～975 hPa 层所占因子明显偏多达9 个，其中以水平风速和垂直速度这两种因子为最多，分别占了4 个和3 个，另外两个因子分别为散度和涡度；因子第二多的层为600～700 hPa，因子总数达到了8 个，其中以气温和比湿为最多，分别占了3 个，其次为垂直速度占了2 个；浮力能因子以600～1 000 hPa 和700～1 000 hPa的相关最好也说明了近中层热力因子的重要性。可见，阵风与低层的动力因子相关较好，而在近中层则与热力因子相关较好。

表1 各站不同天气要素与阵风相关检验的p 值均值在0.05 以下的因子f：水平风速；t：气温；v：涡度；w：垂直速度；d：散度；q：比湿；b：浮力能。

虽然相关性良好的准因子很多，但由于许多准因子彼此之间相关性好，都放到预报模型里面会导致信息的重复利用，导致模型训练拟合好，但预报会变得不稳定，因此最好将相关不显著的准因子挑选出来，使预报模型尽可能保留更多差异化信息，提高预报的稳定性。表2 为准因子之间相关检验p值的平均情况，先考虑同一类型变量选择一个因子，由于p均值越大，相关性越小，故选取p平均值大的准因子；此外，由于低层的水平风速和垂直速度与阵风相关性为最好，因此模型入选低层因子w975 和f1000，以增加这两种类型因子的权重系数。最终入选的预报因子包括875 hPa 散度（d875）、975 hPa 垂直速度（w975）、500 hPa 比湿（q500）、600 hPa 气温（t600）、600 hPa 垂直速度（w600）、700～1 000 hPa 的 浮 力 能（b700_1000）、925 hPa 水平风速（f925）、1 000 hPa 的水平风速（f1000）。

表2 准因子之间相关检验p 值的平均 要素说明同表1。

为了说明入选因子对阵风影响，对比四个站阵风风速最大的10 个样本和风速等于10.1m/s的小值样本所对应的入选因子的平均值情况，表3和表4 为统计结果，可见大值样本阵风风速普遍在25m/s 左右，比小值样本约大1.5 倍，对应的925 hPa 和1 000 hPa 风速也有类似的特征；875 hPa 散度大值样本具有明显更强的辐合，四个站的散度均≤-10.0×10-6s-1，而嵊泗站的小值样本甚至可能表现为辐散；大值样本600 hPa 垂直速度具有更明显的上升速度，而嵊泗站和大陈岛站的小值样本甚至表现为下沉速度，低层975 hPa 的垂直速度则刚好相反，大值样本具有明显更强的下沉速度，东矶站和南麂站的小值样本甚至出现上升运动；从500 hPa 比湿和600 hPa 气温来看，大值样本一般拥有更大的比湿和更高的气温，且700～1 000 hPa 的浮力能也偏大。可见，阵风大值样本在低层具有更强的下沉速度，有利于上层动量向下输送，且大值样本在中层的气温和比湿相对大些，说明中层暖湿气流更加有利于湍流发展和不稳定能量的交换。

表3 四个站点前10 个阵风风速最大样本的入选因子平均值情况 要素说明同表1。

表4 四个站点10 个阵风风速为10.1m/s 小值样本的入选因子平均值情况 要素说明同表1。

4 阵风预报模型试报

高斯过程回归预报模型使用的8 个因子见表3，为了保证模型试报结果的可靠性，试报采用交叉循环检验方案，将样本资料等分为四组，先使用四分之三的资料进行拟合，其余四分之一的资料进行试报，然后进行检验，完成后将原先四分之一的试报样本并入拟合样本，而原来拟合样本则拿出四分之一进行试报，这样重复实验四次得到最终试报结果。模型使用的指数内核协方差函数定义为：

σm对应不同因子的权重尺度，σf为阵风自然对数的标准差，d 为因子数，可见权重尺度σm越大的因子对预报结果的影响越小。图5 为四个站的预报模型对应的8 个因子的权重尺度对数的情况。可见，南麂站因子之间的权重尺度相差不大，相对重要的因子序列为第2、6、7、8；大陈岛站和东矶站因子之间的权重尺度具有明显差异，大陈岛站起主要作用的因子序列为1、2、7、8，而东矶站则为3、6、7、8；嵊泗站因子之间的权重尺度差异也较明显，重要的因子序列为第1、5、7、8。总体来说，第一重要的因子为序列8（1 000 hPa 风速），其次为序列7（925 hPa 风速），然后是序列1（875 hPa 散度）、序列2（975 hPa 垂直速度）、序列6（700～1000 hPa 浮力能），可见最佳预报因子绝大多数集中在875 hPa 层以下，说明大气低层因子对地面阵风起主导作用。

试报结果见表5，可见各站拟合样本和测试样本的绝对误差基本一致，预报模型性能稳定，预报效果大陈岛站和嵊泗站最好，绝对误差为1.4～1.5m/s，南麂站要差一些为1.7m/s，从75%概率区间的跨度来看，东矶、嵊泗、大陈岛站为4.2～4.5m/s，而南麂站则偏大为5.3m/s，类似的50%概率区间东矶、嵊泗、大陈岛站为2.4～2.6m/s，而南麂站则明显增大至3.1m/s，从击中概率上来看，四个站75%概率击中率和50%概率击中率均符合预期。图6 为一组样本10m阵风与1 000 hPa 风速的散点图，黑色点为样本实况，蓝色点为确定性预报，红色点为75%概率区间预报的上限和下限，可见东矶、嵊泗、大陈岛站概率上下限没有明显发散，预报效果好，而南麂站上下限点发散，预报效果一般。图7 则为另一组样本50%概率区间的上限和下限的预报情况，同样东矶、嵊泗、大陈站预报效果比南麂站要好，这可能与南麂站位于浙江南部更加容易受南支天气系统影响，其预报因子与另外三站有所差别导致，从图5 也可以看出南麂站各因子之间的权重尺度大小相差不明显，没有表现突出的预报因子。此外，四个站高斯过程回归方法预报的75%和50%概率击中率则均符合预期。

表5 四个站点预报模型的拟合和测试结果

图6 四个站一组样本10m阵风与1 000 hPa 风速的散点图黑色点为样本实况，蓝色点为确定性预报，红色点为75%概率区间预报的上限和下限。

图7 四个站一组样本10m阵风与1 000 hPa 风速的散点图黑色点为样本实况，蓝色点为确定性预报，红色点为50%概率区间预报的上限和下限。

5 结 论

阵风成因复杂，普遍认为与大尺度风、湍流和稳定度等因子有密切关系，气流的水平动量传输及对流拖拽导致的垂直动量传输均扮演了重要角色，业务中准确定量预报存在困难。本文在统计浙江沿海海岛阵风因子和阵风风速的概率分布特征基础上，在分析阵风的影响因子后，采用高斯过程回归方法建立试报模型，得出以下结论。

(1) 在相同平均风速情况下，阵风因子可以有较大变化，导致对应的阵风也出现大的差异，说明阵风数据分布具有混沌性；阵风风速具有正态或准正态分布特点，在自然对数处理后其数据完全符合正态分布；阵风的数据特征表明采用高斯过程回归的概率预报方法合理可行。

(2) 从不同层次阵风高相关因子数目来看,900～975 hPa 层所占因子明显偏多，其中以水平风速和垂直速度这两种因子为最多；第二多的层次为600～700 hPa，其中以气温和比湿这两种因子为最多，浮力能因子也以600～1 000 hPa 层和700～1 000 hPa 层相关最好。说明阵风与大气低层的动力因子相关较好，而在近中层则与热力因子相关较好。

(3) 样本合成分析表明，阵风大值样本在大气低层具有更强的下沉速度，有利于上层动量向下输送，且大值样本在中层的气温和比湿相对大些，说明中层暖湿气流更加有利于湍流发展和不稳定能量的交换。

(4) 模式的因子权重尺度分析表明，第一重要的因子为1 000 hPa 风速，其次为925 hPa 风速，然后是875 hPa 散度、975 hPa 垂直速度、700～1 000 hPa 浮力能，可见最佳预报因子绝大多数集中在875 hPa 层以下，说明大气低层因子对地面阵风起主导作用。

(5) 高斯过程回归模型试报样本的绝对误差平均为1.5m/s，大部站点样本试报的50%概率区间跨度约为2.5m/s，75%概率区间跨度约为4.5m/s，样本的50%和75%概率区间击中率均符合预期。