粉质粘土层冻结温度场-声场耦合数值模拟及实测研究

，，，

(1.煤炭科学研究总院，北京 100013；2.北京中煤矿山工程有限公司，北京 100013；3.煤矿深井建设技术国家工程实验室，北京 100013)

人工冻结法在井筒施工中被广泛应用[1]。在冻结法施工中，人工冻结壁一旦不稳定和发生破坏将给掘进工作带来巨大的隐患，不及时发现处理将造成严重的后果。目前，常用的判断冻结壁发育状况的方法主要包括经验公式法、水文孔水位法、测温法等[2]。以上方法虽然能够判断冻结壁的整体发育状况，但是当冻结壁局部出现不交圈现象时，受水文孔、测温孔布置位置的影响，推算的结果往往存在一定偏差。因此，需要一种更加直观的方式作为补充手段来判断局部冻结壁的发育状况。

超声波在穿透土体后，会携带大量信息，包括声时、声速、波幅、频率、波形等，这些信息能够反映出土体的岩土力学性质[3]。杨平等[4]认为可以通过冻土力学特性与声波特性的相关性研究找到不同条件下冻土强度与声波参数间的关系，利用该关系可实现现场原位检测冻土声参数来推算冻土的强度。王大雁等[5]认为土质颗粒的大小及组成成分在土冻结且在温度继续下降的过程中，通过影响结合水含量的变化而影响未冻水含量的变化，从而进一步影响冻土中的超声波传播速度。这就为利用超声波检测冻结壁发育状况提供了基础。

本文利用COMSOL Multiphysics有限元软件建立冻结壁温度场与超声波声场单向耦合模型，从数值模拟的角度讨论不同冻结阶段超声波声学信号的响应特征，进而利用不同冻结阶段下声学参数的变化判别冻结壁发育状况，并通过现场检测进行了验证，为人工冻结壁超声波检测技术提供依据。

1 工程概况

河南赵固二矿西风井采用冻结法凿井施工，井筒净直径6.0m，井口标高+81.0m，落底标高-833.0m，设计深度914m，其中井筒穿过冲积层厚度为704.6m。据地质勘查资料，井筒所处地层地下22.3～194.9m主要为粉质粘土层。该矿采用多圈孔冻结方案，冻结孔主要技术参数见表1。

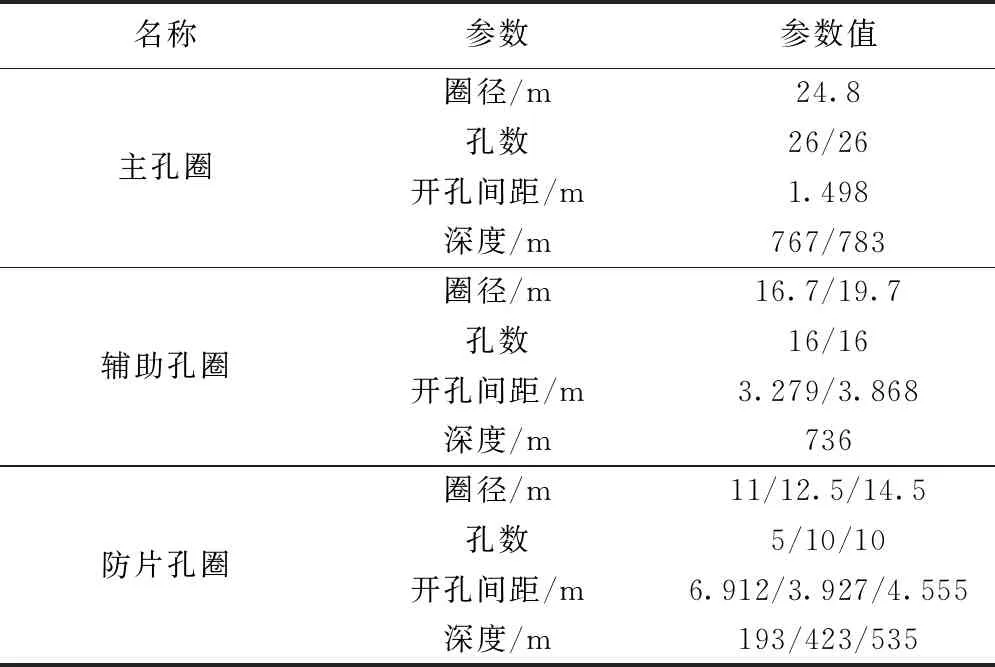
表1 冻结孔主要技术参数

为了检测冻结过程中温度场的变化，布置测温孔T3和T4，孔深均为783m，T3距离主孔圈1.5m，T4距离辅助孔圈1.0m，冻结孔及测温孔布置如图1所示。

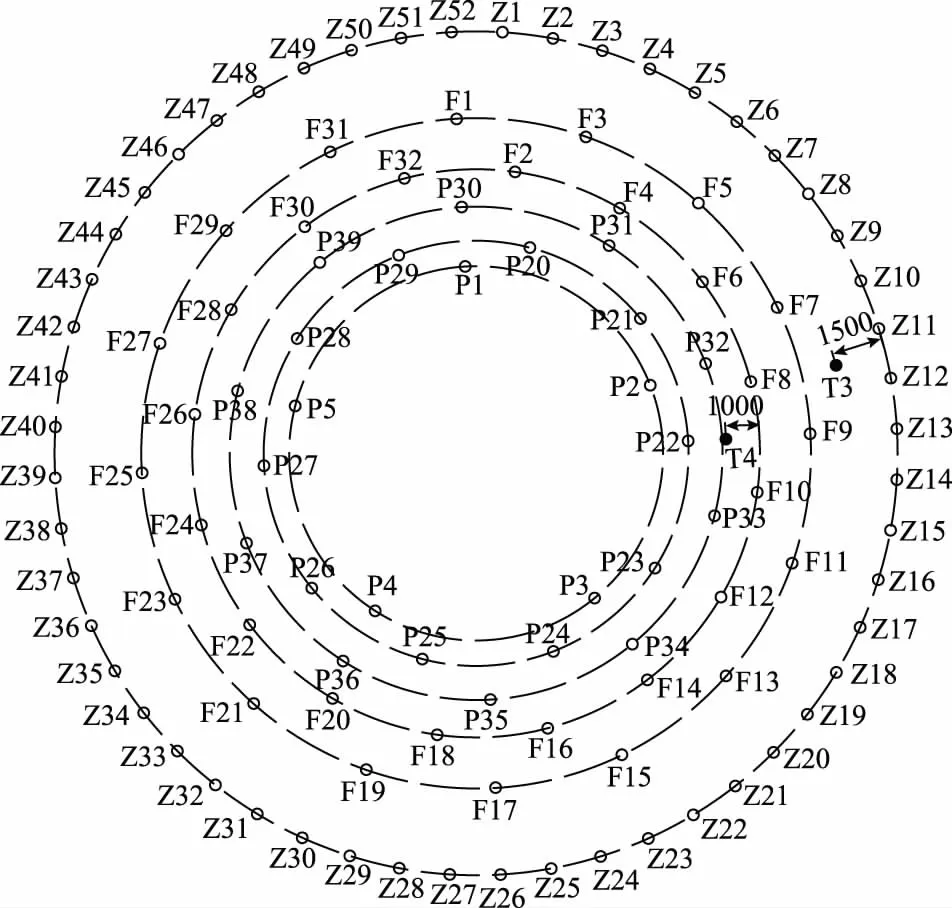
图1 冻结孔及测温孔布置图

2 冻结温度场-声场耦合数值模拟

2.1 基本控制方程

1)温度场的控制方程[6]。均质各向同性体遵循导热方程为：

式中，ρ为密度，kg/m3；Cp是恒压热容，J/(kg·K)；T为表面温度，K；u是节点平移运动的速度矢量，m/s；q是热传导的热通量，W/m-2；qr是热辐射的热通量，W/m2；Q是热源，W/m3；k是导热系数，W/(m·K)。

冻结过程中不考虑辐射换热，故qr项取为0；为节约计算时间，将问题简化为平面二维模型，dz取1mm。因此式(1)可简化为：

2)声场的控制方程。声波在无损介质中的波动方程为[7]：

式中，ρ为介质密度，kg/m3；c为声波在介质中的传播速度，m/s；p为自变量声压，Pa；t为时间，s；qd为偶极子声源，N/m3；Qm为单极子声源，1/s2。

利用人工冻土超声波室内实验方法[4，5]，获得超声波纵波速Vp与温度T的关系表达式为：

Vp=a1+a2T+a3T2

(4)

将式(4)代入到式(3)中可得：

声阻抗Z与波速Vp的关系表达式为：

Z=Vpρ

(6)

将式(4)代入式(6)中可得：

Z=(a1+a2T+a3T2)ρ

(7)

式中，T为温度；Vp为超声波纵波波速；Z为声阻抗；ρ为密度；a1、a2、a3为相关系数。

2.2 冻结粉质粘土声学特性试验

试验土质为粉质粘土，取自河南赵固二矿。按照《土工试验方法标准》(GB/T 50123—1999)进行含水率、密度试验，测定土样的含水率为37.53%、密度为1.87kg/cm3。

土样经过烘干、机械碾碎，过2mm筛并除去杂质。配置时在土样中拌合适量蒸馏水，让土样达到目标含水率，并封闭放置至少12h使土样中的水分充分均匀。待土样中水分均匀后，制成直径为61.8mm、长度为150mm的试样。将制作好的试样装入特制的模具中，然后放入温度低于-20 ℃的恒温箱中快速冻结，24h后脱模，重新测定脱模后试样的尺寸和质量。再将试样放入控温精度为±0.02℃的控温恒温箱中，当温度达到设计温度时进行超声波测试，每个试块均测试三次取平均值。分别获得了不同温度条件(-1℃、-3℃、-5℃、-7℃、-10℃、-15℃、-20℃)下的波速值。超声波测试采用NM-4A非金属超声波检测分析仪，纵波换能器的频率为50kHz，采用凡士林作耦合剂。

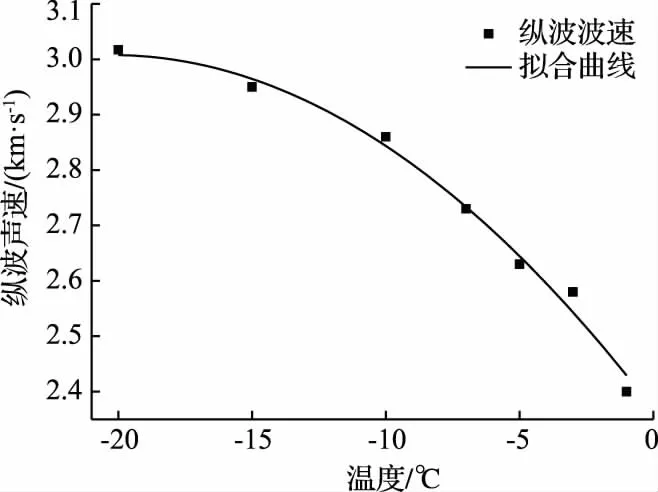
图2 纵波声速与温度关系曲线图

测得的纵波声速与温度的关系曲线如图2所示，波速与温度之间呈非线性关系，利用二次函数进行拟合，回归波速与温度关系表达式为：

Vp=a1+a2T+a3T2

式中，a1=2.3675，a2=-0.0632，a3=-0.00156。

2.3 热声单向耦合模拟方案

利用COMSOL Multiphysics软件对超声波在井筒冻结壁中的传播过程进行模拟，采用固体传热和压力声学模块，进行热-声单向耦合数值模拟计算。首先，基于式(2)进行人工冻结热力学分析，获得不同冻结阶段的温度场分布云图。其次，利用人工冻土超声波室内实验获得土层温度与纵波波速的关系表达式(4)，结合声阻抗与纵波波速的关系式(6)，将温度场分布云图转变为声阻抗分布云图，并将关系式(5)、(7)输入到求解域中。最后，进行声压场的时域瞬态计算，提取声压、波速进行分析。

2.4 热声单向耦合模型

根据实际冻结孔的布置，经过适当简化处理，按平面问题考虑冻结温度场。求解域直径为60m×60m，选用COMSOL Multiphysics软件固体传热模块进行数值模拟，模拟冻结天数90d，有限元模型如图3所示。

图3 冻结井筒有限元模型

以粉质粘土层为主要研究对象，热物理参数见表2。

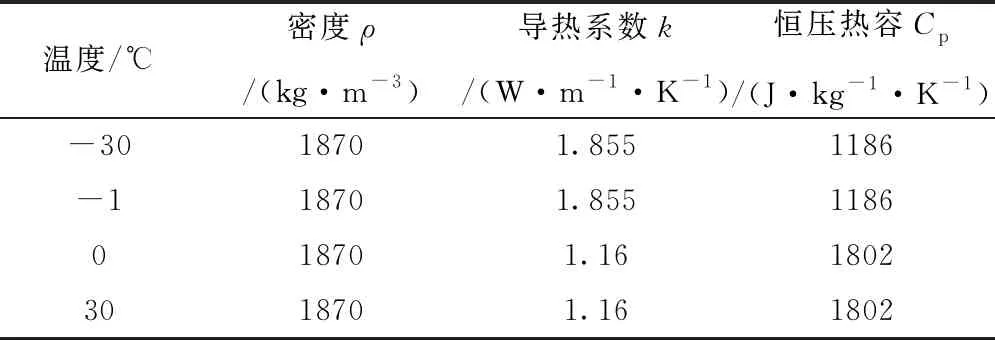
表2 粉质粘土热物理参数

根据相关资料初始地温设置为20℃，在所有冻结管外壁施加温度边界条件，冻结管外壁温度近似成盐水温度，其中盐水降温曲线如图4所示。

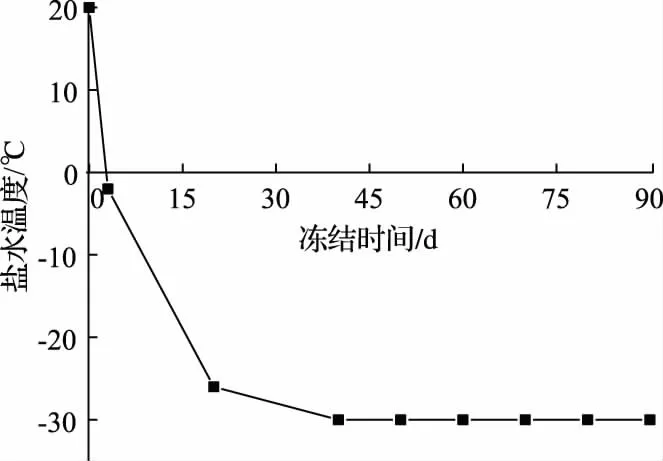
图4 盐水降温曲线

在对不同冻结阶段的冻结壁进行超声波检测时，重点关注的是相邻两冻结孔之间的声场分布，为了减少计算量，以井筒最上方的主冻结孔(Z1)以及其相邻孔(Z2、Z52)为研究对象，调取两冻结孔之间的温度场分布，以主冻结孔Z1为发射中心，主冻结孔Z52为超声波信号接收端，如图5所示。

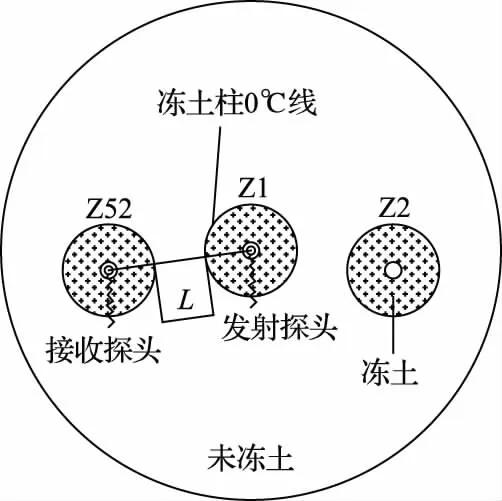
图5 两孔超声波检测示意图

选取超声波声源S(t)的函数表达式[7]为：

πf0t)

(8)

式中，t为声时，s；f0为声源中心频率，Hz；T0为周期，s。此信号的函数如图6所示。

声源激励选用柱面波辐射，施加在Z1冻结孔的边界上，作用时间为一周期；外边界设为低反射边界，声波到达后不会反射，以模拟声波在无限大土体中的传播。一般而言，单元网格大小由声源决定。很多研究计算表明，当单元网格小到一定程度后，继续缩小单元网格大小对提高计算精度的效果己不显著，在有意义的波长内含有不少于6～8个的空间步长可以满足精度[7，8]。本文选取最小波长的六分之一作为空间步长，经计算确定最大单元格尺寸为1mm，计算时间步长设置为T0/10。超声波声场模拟的相关计算参数见表3。

表3 声学计算相关参数

3 模拟结果分析

3.1 温度场

随着冻结时间的推移，冻结温度场不断向外扩展并开始交圈，周围土体温度逐渐降为0℃，冻土帷幕开始形成，并且厚度不断增加。定义两相邻冻土柱零温线之间的间距，即未交圈距离L，冻结过程中冻结壁(圈)的发展过程以及冻结管附近温度场的变化趋势，如图7所示。可以看出，冻结25d后，L=590mm；冻结40d后，L=81mm；冻结42d后，最外圈相邻主冻结孔连线中心的温度降至0℃以下，冻土帷幕开始交圈；冻结90d后，主冻结圈冻结壁进一步发展，形成一定厚度，而主冻结孔与辅助冻结孔尚未交圈。

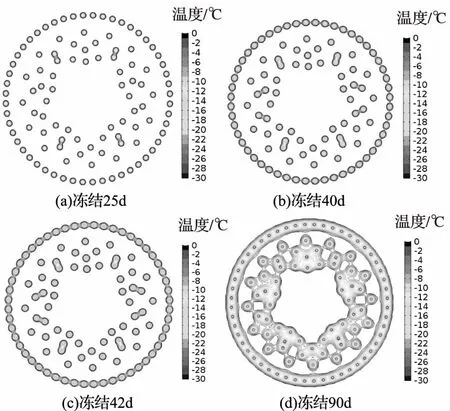
图7 冻结壁温度等值线图

利用COMSOL软件提取测温孔T3、T4所在位置不同时间的温度数据，将模拟结果与实测结果进行比较，绘制温度随时间变化的曲线如图8所示。

式(5)中：和分别为交叉航道中单位时间内某种特定船舶交通流量，艘；和为交叉航道中船舶的航速，m/s；Vij为两船的相对航速，m/s；Dij为当交叉相遇中两船不做任何避让行动条件下碰撞区域直径；θ为航道交叉角度，(°)。

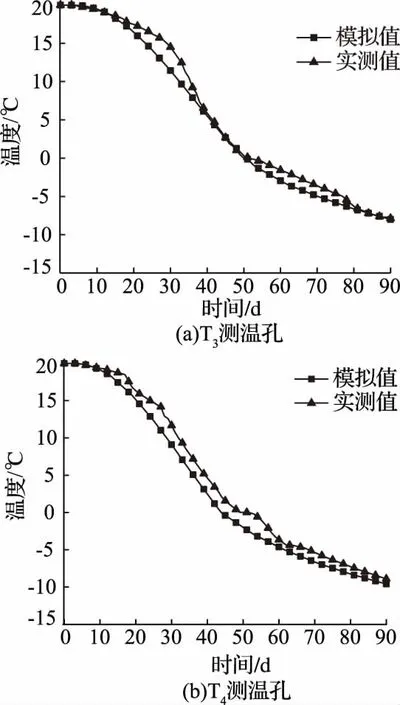
图8 测温孔模拟结果与实测结果对比

煤矿井筒冻结壁温度场的发展受多种因素影响[9-13]，虽然本文中考虑了冻结过程中导热系数及比热容的变化，但是并不能包含所有影响因素。由图8可以看出，模拟温度数据与实测温度随时间的变化曲线虽在个别区段有较小偏差，但两曲线具有相同的发展趋势，均随冻结时间呈对数关系下降。可以认为数值模拟所选参数与本文研究对象的实际情况基本相符，数值模拟的计算结果可在满足工程精度的要求下有效反应实际情况，所选岩土热物理性质参数是合理可信的，能够为温度场与声场的耦合计算提供可靠依据。

3.2 声场

在不同冻结阶段25d、40d、42d、90d设置超声波激励，得到接收点的波形如图9所示，并求得两个冻结孔之间的平均声速。

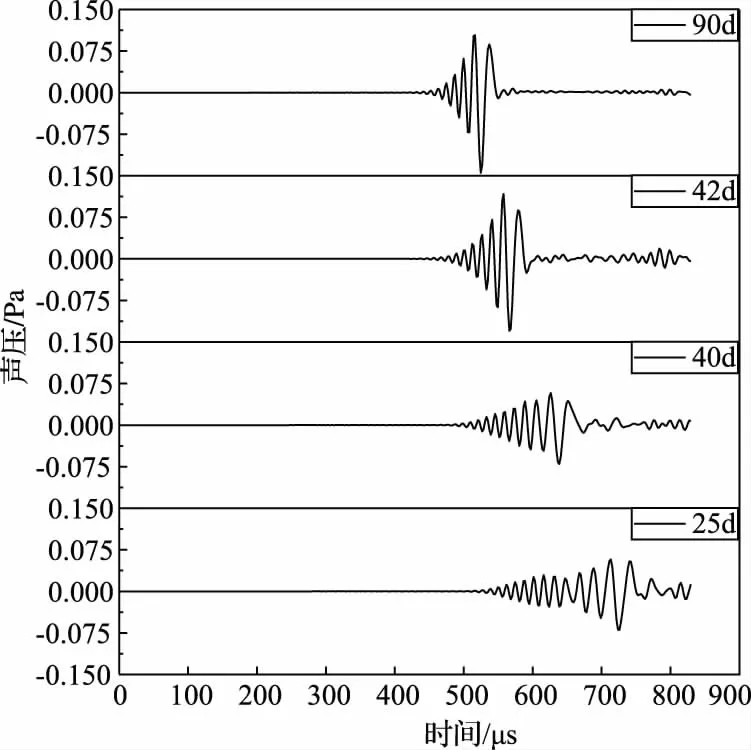
图9 不同冻结阶段接收点波形图

由图9可以直观的看出，冻结25d和冻结40d，即冻结壁交圈之前，波形图发生明显的紊乱与畸变；冻结42d和冻结90d，即冻结壁交圈之后，波形图曲线形态规律完整，峰值突出。冻结前期检测声压值较小，随着冻结时间的增加，声压值逐渐增大，声压衰减逐渐减弱。从COMSOL计算结果中提取出四个冻结阶段的峰值声压，见表4。与冻结90d相比，冻结25d、40d、42d分别衰减51.83%、51.48%、10.29%。其中，冻结30d峰值声压与冻结27d峰值声压相比，峰值声压增大了45.91%，二者差别极大，反映出冻结壁交圈前后声压发生了急剧变化。

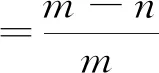
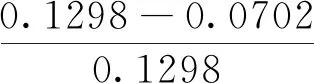
式中，m为30d峰值声压；n为27d峰值声压；ξ为变化量百分比。

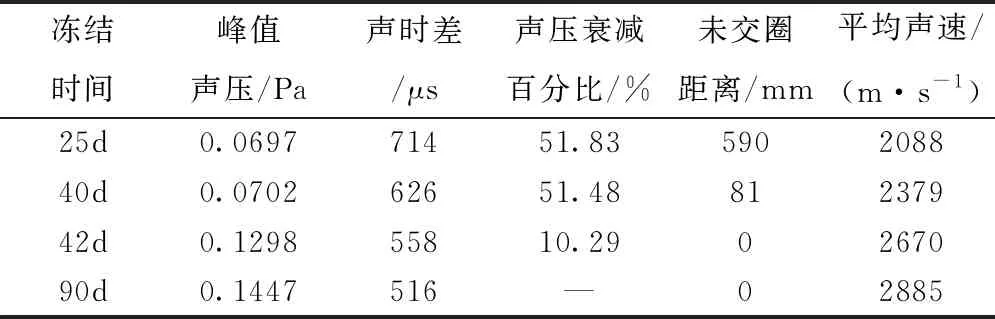
表4 不同冻结阶段声压计算结果对比

4 检测实例

利用NM-4A型超声波检测仪在Z1、Z52孔进行4次超声波检测实验，测试阶段分别为冻结25d、40d、42d、90d。检测层位为-30m的粉质粘土层。

超声波测试采用NM-4A非金属超声波检测分析仪，由声波检测仪、导线、发射和接收换能器组成，纵波换能器频率为50kHz，尺寸为38mm，水密性能可以满足1MPa不渗水(可用于100m水深)。该声波检测仪的采样间隔为0.1～200μs，记录长度为0.5～1K可调，发射电压为500V/800V/1000V可选，放大增益为100dB，发射脉宽为0.1～100μs连续可调，放大器带宽5～500kHz。为了使测试结果具有可比性，整个测试过程声波检测仪的参数(如发射脉宽、增益等)设置一致。

具体测试方法如图10所示，在Z1、Z52两孔内分别下放发射和接收的换能器，下放至供液管中，使两换能器在同一标高上，利用盐水作为耦合剂进行测试。

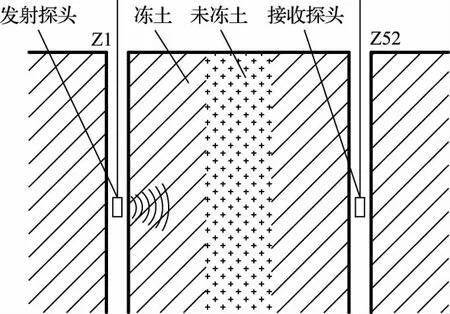
图10 检测示意图

测得的平均声速测试值与模拟值对比如图11所示。可见，测试值与模拟值整体趋势基本一致，测试值普遍较模拟值低5%，原因在于测试耦合剂为低温盐水，与室内实验条件有较大区别；另外，数值模拟时未考虑冻土中的裂隙以及应力状态等因素。因此，实际测试中超声波的衰减相对较大。现场检测结果表明，可根据实测平均声速105%对比温度场-声场耦合数值模拟结果，确定Z1、Z52孔之间未交圈距离。

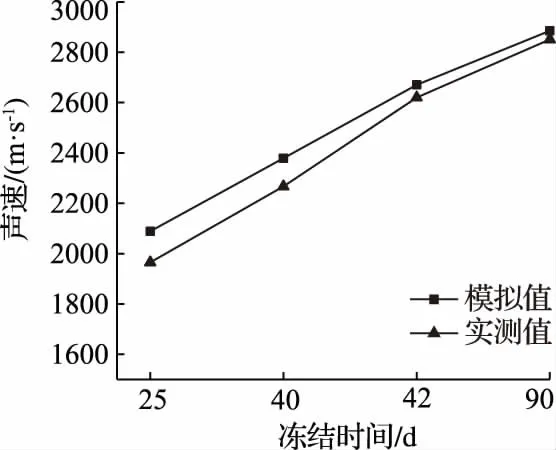
图11 平均声速模拟值与实测值对比

5 结 论

1)采用COMSOL Multiphysics多物理场耦合程序，选取固体传热与压力声学模块，提出了热-声单向耦合仿真思路，建立了温度场-声场间接耦合数值模型。

2)从模拟结果可以看出，冻结壁从未交圈到交圈，超声波波形变化明显，声压急剧增大，42d(交圈)峰值声压比40d(未交圈)峰值声压增大了45.91%，冻结壁交圈前后超声波波形、声压、平均声速均发生剧烈变化，可以有效的判别冻结壁的交圈情况。

3)随着冻结时间的增加，模拟求得的随着量冻结孔之间未交圈距离逐渐减小，超声波平均声速从2088m/s逐渐增加到2885m/s。不同冻结阶段平均声速变化趋势与实测值基本一致，绝对值相差5%。表明温度场-声场耦合数值模拟方法可作为预测不同冻结阶段冻结壁超声波声学参数的有效手段。