复杂环境下BDS/GPS紧组合高精度定位方法

隋 心，李玉星，沈佳琦，张 涵，杨东辉

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

0 引言

目前，在室外良好观测环境下利用全球卫星导航系统(global navigation satellite system，GNSS)可以很容易获得较高精度的定位结果[1-5]，但是在复杂观测环境下，例如城市峡谷，GNSS的定位性能大幅下降，其主要原因为城市峡谷中高大建筑物对GNSS信号的遮挡与反射。在一些特别复杂的观测环境下，单GNSS系统的可观测卫星的个数甚至会低于4颗，这将导致GNSS无法定位。因此有必要对复杂观测环境下GNSS高精度定位进行研究。

随着卫星导航定位技术的快速发展，很多国家都致力于建立各自的卫星导航定位系统，目前已有多个GNSS系统处于运行状态，已经建成的全球卫星导航系统包括美国的全球定位系统(global positioning system，GPS)和俄罗斯的格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)，处于建设阶段的包括我国的北斗卫星导航系统(BeiDou navigation satellite system，BDS)和欧盟的伽利略卫星导航系统(Galileo navigation satellite system，Galileo)。随着各国GNSS的不断完善与建设，GNSS卫星的个数也在不断增加。将不同GNSS卫星观测值进行组合可有效解决复杂环境下的高精度定位问题[6-9]。目前，在4个GNSS系统中，GPS、GLONASS和Galileo的卫星星座只包括中圆地球轨道(medium Earth orbit，MEO)卫星，而BDS的星座构成同时包括地球静止轨道(geostationary Earth orbit，GEO)卫星、倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)卫星和MEO卫星，因此在中国及周边区域可保证在天顶方向具有相对多的观测卫星，这对于复杂观测环境下的高精度定位是有益的[10]。同时，GPS在目前4个GNSS系统中发展最为成熟，并且其卫星信号的频率也与BDS十分接近，因此将BDS与GPS进行组合，理论上可以增强复杂环境下定位的实时性、连续性和可靠性[11]。

目前多GNSS组合相对定位分为2种模式，一种为称为松组合，一种称为紧组合。2种组合模式的区别在于松组合只构建系统内部双差观测方程[12]，而紧组合不仅构建系统内部观测方程，同时也构建系统间观测方程[13]。由于紧组合增加了观测方程个数，因此多GNSS紧组合更适合于复杂观测环境下定位。对于实时高精度来说，模糊度固定至关重要。对于GPS和BDS系统内部构建的双差模糊度，它们仍然具有整数特性，可以采用常用的模糊度固定方法对其固定；对于GPS和BDS系统间的双差模糊度，由于存在系统偏差(inter-system bias，ISB)的影响，系统间双差模糊度将很难被固定下来，需要采用一定方法对其分离。此外，ISB的稳定性也比较重要，如果ISB能够保持稳定，可以利用准确计算的ISB值对后继历元的相位观测值进行改正，进而实现紧组合相对定位。文献[14]对GPS/BDS的ISB稳定性进行研究，短基线实验结果表明在5种品牌接收机中有3种品牌的接收机端ISB不稳定，2种品牌的接收机端ISB在较长时间内保持稳定，接收机重启对ISB稳定性产生影响。

本文首先对BDS/GPS的紧组合定位模型进行推导，然后利用实验对ISB的稳定性进行分析，在此基础上，利用真实复杂观测环境下的BDS/GPS观测数据对紧组合定位模型进行检验。

1 BDS/GPS紧组合观测模型

以GPS和BDS非差相位观测方程为基础，推导BDS/GPS紧组合观测模型。在短基线条件下，GPS和BDS的相位观测方程[15]可表示为

(1)

(2)

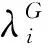
顾及GPS与BDS在时间系统上所存在的差异，式(2)可进一步表示为

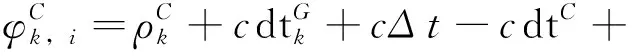
(3)

式中cΔt为BDS和GPS在时间系统上的偏差。

对接收机k和l进行站间求差可得

(4)

(5)

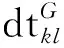
对于松组合，构建双差过程中，分别在各自系统内部选择参考卫星，然后进行卫星间求差，形成的系统内部双差相位观测方程可表示为

(6)

(7)

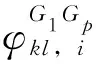
对于紧组合，除了要构建与松组合一致的系统内部双差观测方程，还需要构建系统间相位双差观测方程。为了防止出现秩亏现象，只对GPS和BDS的参考卫星间求差，可表示为

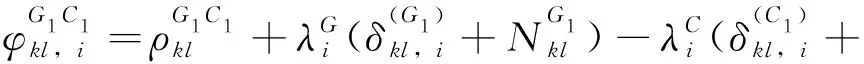
(8)

将式(8)进行变换

(9)

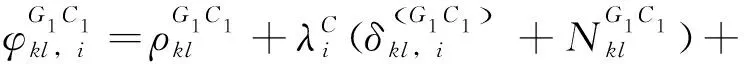
(10)

由于GPS和BDS的第一频段和第二频段波长十分接近，分别为0.190 3 、0.192 0 和0.244 2 、0.248 3 m，如果GPS参考卫星的单差模糊度的计算精度能够分别低于11个周期和6个周期，那么可以忽略由于波长不同对整周模糊度的固定所造成的影响。GPS参考卫星的单差模糊度初值可以根据多历元的P码和载波相位数据进行计算。式(10)可进一步表示为

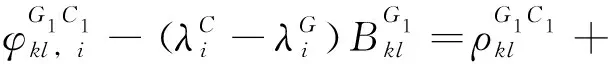
(11)

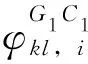
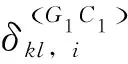
2 复杂观测环境下BDS/GPS紧组合对定位精度影响分析

BDS/GPS在不同频率下的ISB稳定性对于BDS/GPS紧组合定位影响较大，有必要利用实验对ISB的稳定性进行验证。使用2台GNSS接收机采集短基线数据，利用本文所述方法对基线的B1/L1观测数据进行单历元解算，ISB的时间序列结果见图1。

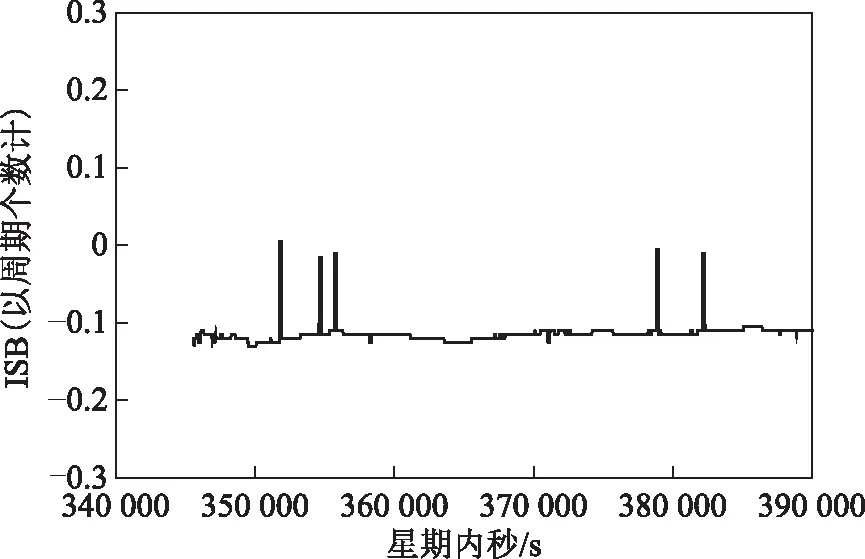
图1 BDS/GPS ISB的时间序列

图1表明解算的ISB值并不为零，均值为-0.113个周期，出现该现象的原因可能为实验采用了2个不同品牌的接收机，已有研究成果也表明不同品牌接收机间的ISB可能不为零[14]。ISB时间序列从总体上来看是比较稳定的，中误差为0.015个周期，小于0.1个周期，因此认为可以将该ISB均值作为已知的校正参数对后继历元相位观测值进行改正，实现紧组合定位。在图1中，出现了5处ISB解算结果大幅偏离均值的情况，由于这部分解算结果在整体解算结果中所占比例十分微小，因此可将其视为异常值予以忽略。为了检测BDS/GPS紧组合对复杂观测环境下定位精度的影响，对真实复杂环境下的观测数据进行采集与解算。

图2 真实复杂观测环境下的测站安置

使用上述实验2台接收机采集一条长为5.1 km的基线，观测数据中包括GPS、BDS单频观测值，采样率为1 s，观测时长为1 h20 min，卫星截止高度角为15°。将1台接收机安置于观测环境良好的广场，将另一台接收机安置于一栋四层楼楼下，测站与楼的距离约为1.5 m，具体安置见图2。观测期间卫星轨迹图和卫星数量及位置精度因子(position dilution of precision，PDOP)值见图3和图4。

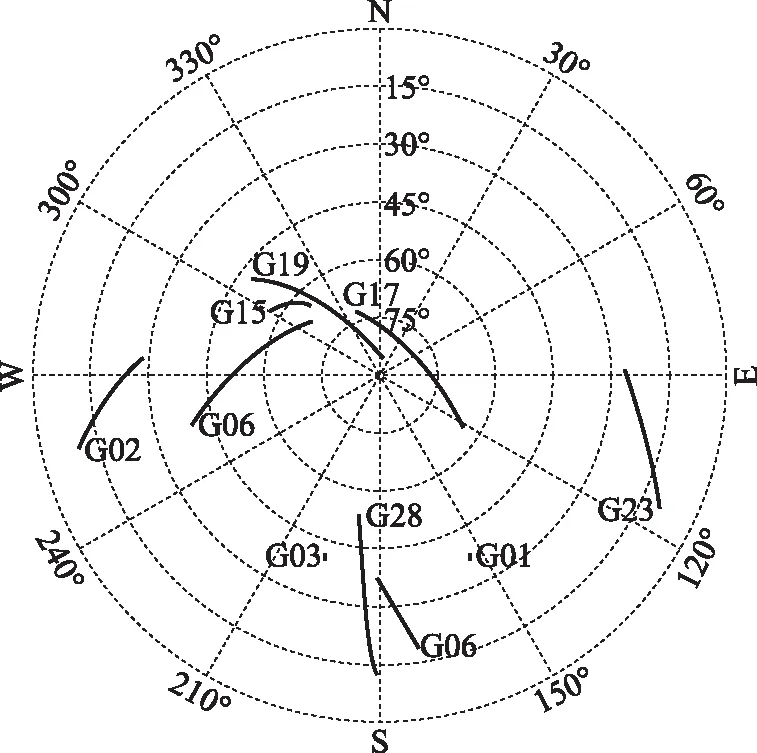
图3 卫星轨迹图

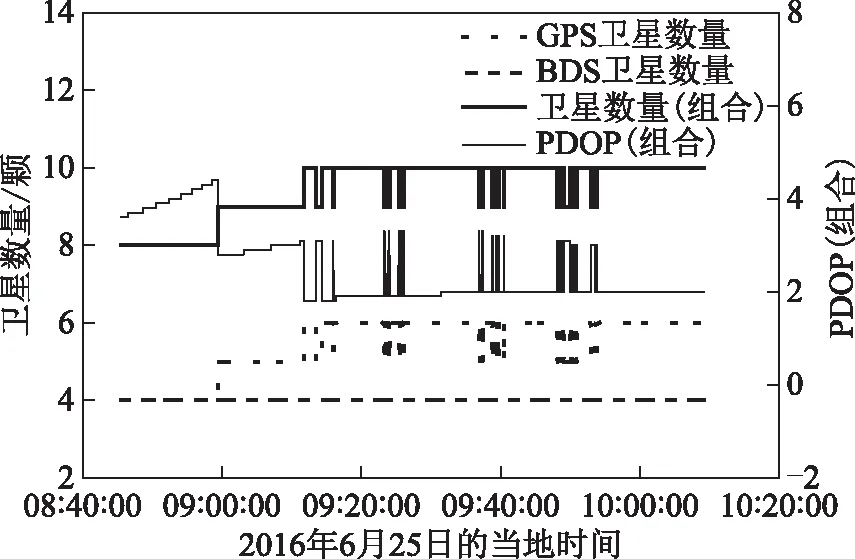
图4 卫星个数和PDOP值

为了能够细致分析复杂环境下紧组合对定位精度的影响，将不同模式下解算结果的定位误差区间分布进行比较。为了能够进一步分析复杂环境下实时计算ISB参数与已知ISB校正参数的定位结果差异，也对这两种模式下的解算结果的定位误差区间分布进行统计。总体统计结果见表1。

表1表明对于单系统，平面和高程定位偏差小于1 cm所占的比例均低于18 %，GPS单系统平面定位偏差小于5 cm所占的比例低于42 %，高程低于38 %，BDS单系统平面定位偏差小于5 cm所占的比例低于50 %，高程低于31 %，GPS和BDS单系统的平面定位偏差小于10 cm所占的比例均接近于50 %，高程均接近于38 %。对于BDS/GPS双系统松组合，相对于单系统定位精度得到一定提高，在小于1 cm区间内，平面接近于70 %，高程接近于40 %，在小于5 cm区间内，平面和高程均接近于80 %，当定位偏差区间放大到小于10 cm和小于20 cm时，平面和高程所占比例已无明显变化。对于已知ISB校正参数的BDS/GPS双系统紧组合，在小于1 cm区间内，该模式所占的比例并不高，平面和高程分别为69.5 %和41.4 %，低于上述松组合所占比例，但当定位偏差区间放大到小于5 cm时，平面和高程所占比例均接近于100 %，出现该现象的原因主要是在该模式下，始终将ISB校正值设置为一个固定的值，而该值是根据时段内所有历元的ISB求均值而获得，因此在部分历元上，设置的ISB校正值并不是当前历元所需ISB的最优值。对于实时计算ISB参数的BDS/GPS双系统紧组合，在小于1 cm区间内，该模式所占的比例高于松组合和已知ISB校正参数的紧组合，平面和高程分别为73.3 %和62.7 %，因此可以认为采用实时计算ISB参数的紧组合模式，可以获得更加精确的定位结果。当定位偏差区间放大到小于5 cm时，实时计算ISB参数的紧组合模式所占比例高于松组合，但低于已知ISB校正参数的紧组合模式。出现该现象的可能原因为在复杂观测环境下可观测卫星个数减少，采用紧组合可以增加多余观测值个数，因此无论是实时计算ISB参数的紧组合模式还是已知ISB校正参数的紧组合模式，它们在小于5 cm的区间内所占比例都高于松组合。但对于实时计算ISB参数的紧组合模式，为了能够进行紧组合该模式还需要额外增加1个ISB参数，这将削弱整体平差模型强度，最终导致该模式所占比例低于已知ISB校正参数的紧组合模式。根据以上实验结果分析，可以认为本文所述方法可较好地解决复杂环境下的高精度定位问题。

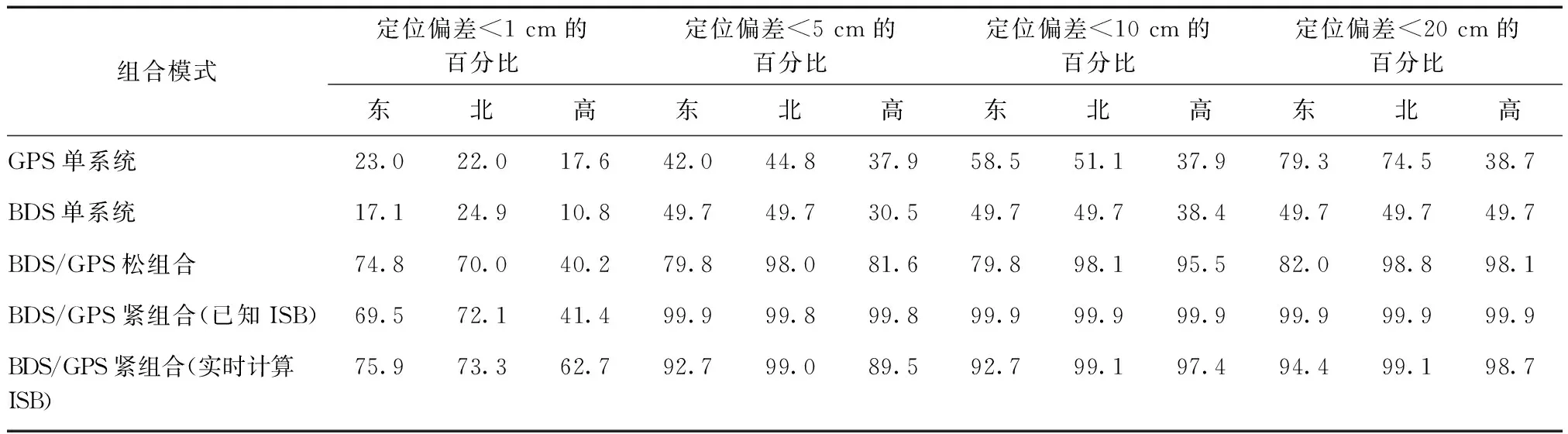
表1 真实复杂观测环境下不同模式下解算结果的定位误差区间分布比较 %

3 结束语

随着导航定位技术的不断进步，人们越来越关注于复杂环境下的高精度定位，BDS/GPS紧组合定位是一个较好的选择。本文以GPS非差观测方程为基础，推导出顾及ISB的BDS/GPS紧组合观测方程。利用实验对ISB稳定性进行分析，实验结果表明ISB具有稳定性，可以作为校正参数。为了检验BDS/GPS紧组合对复杂观测环境下定位精度的影响，将不同模式下解算结果的定位误差区间分布进行比较分析，BDS/GPS紧组合的平面和高程定位偏差小于5 cm所占的比例均接近于100 %，而松组合的平面和高程定位结果在该区间所占比例均约为80 %，紧组合相较于松组合提高了20 %。