BDS三频非差RTK单历元定位方法

刘 扬，程鹏飞，徐彦田，张洪文

(1.辽宁工程技术大学，辽宁 阜新 123000；2.中国测绘科学研究院，北京 100830；3.黑龙江第一测绘工程院，哈尔滨 150025)

0 引言

我国北斗卫星导航系统(BeiDou navigation satellite system，BDS)是首个能全星座播发三频信号的导航卫星系统。三频信号相比单频或双频信号，在周跳探测和等模糊度解算方面都具有更大的优势。实时动态定位(real-time kinematic，RTK)技术已经成为全球卫星导航系统(global navigation satellite system，GNSS)高精度实时动态定位领域一种不可替代的定位方法，并且得到了广泛的应用[1]。RTK通过消除或削弱流动站的观测误差来提高定位精度。经过消除大部分误差的流动站只需解算位置参数和模糊度参数即可，可实现单历元定位。

为了缩短定位初始化时间和提高模糊度解算的成功率、可靠性，文献[2]研究了一种BDS单历元基线解算方法，模糊度解算成功率还可进一步提高。文献[3]通过无几何模式逐步解算2个超宽巷模糊度，在通过几何模式固定第3个超宽巷最后还原到原始载波模糊度进行定位，可尝试其他较优的组合系数。文献[4]研究了估计对流层延迟误差和电离层延迟误差参数的BDS中长距离的非差RTK定位算法，单基站非差RTK方法将大气误差参数化后模糊度解算成功率较高。文献[5]研究了一种基于宽巷观测值的中基线单历元分米级定位方法，未解算基本频点模糊度。

为了利用三频观测量组合长波长、低噪声的优势，本文在研究三频模糊度解算的基础上，编写程序实现单参考站RTK流动站观测值的非差误差改正，单历元计算2个超宽巷模糊度，进而线性组合得到宽巷模糊度，对基本频点构成约束，通过最小二乘模糊度降相关平差法(least-square ambiguity decorrelation adjustment，LAMBDA)辅助固定基频单差模糊度解算进行实时动态定位。

1 流动站误差改正方法

1.1 参考站非差误差改正数的计算

RTK参考站坐标已知，可以计算出伪距及载波相位观测值的非差误差改正数，由于对流层延迟、电离层延迟和卫星轨道误差等具有空间相关性[6]，故可以通过计算参考站误差来消除或大大削弱流动站观测误差对模糊度解算的影响，使其残余误差影响小于半个波长。

基准站伪距和载波相位观测值的非差改正数(undifferenced observation minus computed，ud-omc)为

(1)

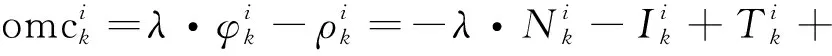
(2)

式中：omcp为伪距观测值改正数，以m为单位；上标i为卫星编号；下标k为接收机编号；omc为载波相位观测值改正数，以m为单位；λ为BDS观测值的波长，以m为单位；P为伪距观测值，以m为单位；φ为载波相位观测值，以周跳个数为单位；ρ为卫星至接收机几何距离，以m为单位；N为整周模糊度，以周跳个数为单位；I为电离层延迟误差；T为对流层延迟误差；c为真空中的光速；t为钟差，上标ti表示卫星钟差，下标tk表示接收机钟差；εP为伪距观测值噪声；ε为载波相位观测噪声，以m为单位。改正数中包含误差改正信息和基准站的整周模糊度，基准站的整周模糊度改正后可以吸收到流动站整周模糊度中。

1.2 流动站观测值的非差误差改正

流动站卫星i，j经非差误差改正数改正后的伪距和载波相位观测方程为

(3)

(4)

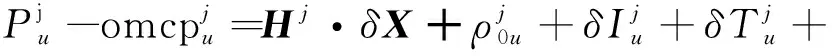
(5)

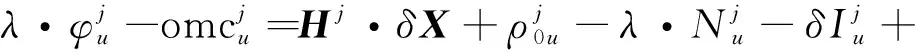
(6)

式中：Hi为流动站点处卫星的方向余弦矩阵；δX为流动站点坐标改正向量；ρ0表示接收机至卫星近似距离；流动站经过改正消除了卫星钟差和卫星硬件延迟，δI和δT为残余的电离层和对流层延迟误差，短基线情况下可以忽略。将式(3)至式(6)星间求差消除流动站钟差tu和基准站钟差tk得到

(7)

(8)

式中：上标i、j表示流动站i和j卫星做星间单差。按照上述改正方法可得到当前历元所有观测卫星的经过误差改正的伪距及载波相位单差观测方程，经过改正后的载波相位单差观测方程中只含有位置参数和模糊度参数。短基线单参考站非差RTK达到与双差RTK差分定位等效的误差消除效果，但非差模式更灵活，以接收单颗卫星非差误差改正数的形式对流动站进行误差改正。

2 流动站BDS三频单历元模糊度解算

2.1 超宽巷和宽巷模糊度求解

以周跳个数为单位的三频载波相位线性组合观测量为

φ(l,m,n)=l·φ1+m·φ2+n·φ3

(9)

式中：l、m、n为整数组合系数；φi为第i个频点的载波相位观测值。以距离为单位的伪距线性组合观测量为

(10)

式中：Pi为第i个频点的伪距观测值；f1、f2、f3为BDS信号的频率，分别对应于B1=1 561.098 MHz、B2=1 207.14 MHz、B3=1 268.52 MHz。

计算涉及到的载波相位超宽巷组合如表1所示。

表1 所选取超宽巷载波相位组合特性

超宽巷组合(0，-1，1)总噪声水平在中基线情况下低于0.3 个周跳，可以忽略大气误差的影响[7]。超宽巷组合选取电离层放大因子较小的(1，2，-3)，在电离层残余误差δI小于等于20 cm时为较优的超宽巷组合[8]，短基线情况下流动站观测值经过误差改正残余电离层延迟误差一般不会超过20 cm[6]。

所选取的相关伪距计算组合如表2所示。

表2 相关伪距组合特性

第一个超宽巷模糊度ΔN(0,-1,1)为

(11)

式中：Δ为单差算子；下标round-off为四舍五入取整。观测量组合PC-I与EWL-I的电离层放大因子与噪声放大因子相同，故消除电离层延迟一阶项影响和对流层延迟影响，进而可直接取整为最近的整数固定模糊度。超宽巷组合(0，-1，1)通过式(11)单历元解算成功率接近100 %[6]。

第二个超宽巷组合(1，2，-3)与EWL-I组合噪声放大因子相近，故将去掉整周模糊度信息的EWL-I组合观测值作为虚拟伪距观测值参与解算，采用基于几何模型为

(12)

(13)

PC-II与EWL-III的电离层放大因子不相同，因此还有残余的电离层延迟误差，但对流层延迟差可以消除[5]。宽巷模糊度的解算可采用超宽巷模糊度线性组合，宽巷模糊度解算的成功率取决于第二个超宽巷模糊度解算的成功率。本文采用第一种组合求解，其计算方法为

(14)

(15)

2.2 基本频点B1模糊度求解

采用宽巷模糊度组合(1，-1，0)和(1，0，-1)约束B1、B2、B3观测值分别构建原始载波相位单差观测方程[9]，可得到一个观测卫星对的B2单差观测方程为

(16)

式中：ΔN1为待求B1频率的单差模糊度参数；L为观测值减近似值所得残差；下标表示频率，B3与B2相似。由于流动站观测值经过非差误差改正后，消除了绝大部分大气误差及卫星轨道误差，L主要包含该频率的未知整周模糊度信息，解算中通过宽巷模糊度分解为基频模糊度线性组合，可实现对基频模糊度求解的约束，提高解算成功率，列立一个历元所有观测卫星对的B1、B2、B3单差观测方程。

BδY=L

(17)

式中：Β为位置参数与模糊度参数系数矩阵；Y为位置与模糊度参数矩阵；L为残差向量。采用最小二乘法求解方程为

δY=(BTPB)-1BTPL

(18)

式中P为权矩阵，依据卫星高度角得出。用去除模糊度信息的宽巷观测值对基本频点模糊度求解构成约束，使得观测方程的状态大为改善，使用LAMBDA方法固定模糊度，通过Ratio检验判定基频模糊度固定情况[10]，模糊度固定后回代入观测方程，得到固定解。

3 实验与结果分析

本文采用的数据是利用Trimble R10多频接收机在河北省采集的2条基线：一条50 m的超短基线，连续观测约2 h，采样间隔为1 s，观测时间为2017年9月15日；一条7 km的短基线，连续观测约1 h，观测时间为2017年9月16日。编写程序实现上述算法采用动态数据的单历元方式处理，流动站位置精度衰减因子(position dilution of precision，PDOP)如图1～图2所示。

图1 50 m超短基线流动站PDOP值

图2 7 km短基线流动站PDOP值

从图1～图2可以看出，50 m超短基线PDOP值在1.9和2.5之间浮动，最大不超过3，观测条件较好，7 km短基线PDOP值从2.2持续升高，最大不超过3，卫星几何构型逐渐变差，观测条件一般。图3～图8为解算各个历元所有星间单差卫星对的超宽巷小数部分。

图3 50 m超短基线超宽巷组合EWL-Ⅰ小数部分

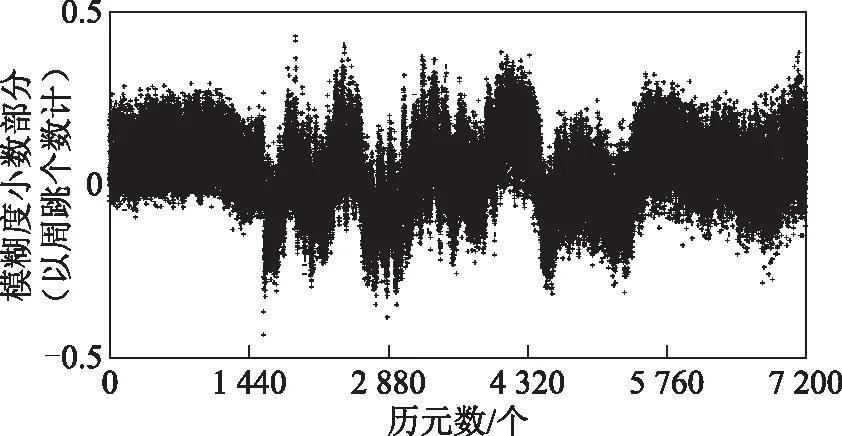
图4 50 m超短基线超宽巷组合EWL-Ⅱ小数部分

图5 50 m超短基线超宽巷组合EWL-Ⅲ小数部分

图6 7 km短基线超宽巷组合EWL-Ⅰ小数部分

图7 7 km短基线超宽巷组合EWL-Ⅱ小数部分

图8 7 km短基线超宽巷组合EWL-Ⅲ小数部分

EWL-I组合在2条基线中的模糊度小数部分绝大多数都在0.3 个周跳以内，2条基线采用无几何模型解算的EWL-III组合(1，4，-5)的收敛程度没有经过虚拟值进行约束求解的EWL-II组合(1，2，-3)的收敛程度优，但取整仍能得到出正确的模糊度。

2条基线解算模糊度求得的Ratio值如图9～10所示。

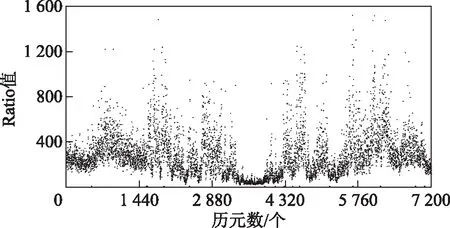
图9 50 m超短基线的Ratio变化

图10 7 km短基线的Ratio变化

50 m基线距离非常短，流动站观测值误差消除较好，残余电离层延迟误差、对流层延迟误差和卫星轨道误差都很小，改正后的流动站观测值质量较高，解算模糊度Ratio值很大。7 km短基线可能由于观测时间段内卫星几何构形逐渐变差，Ratio值逐渐变小。将高精度解算软件处理2条基线结果作为真实值，计算结果与真实值作差得到东(E)、北(N)、天(U)3个方向的误差值，如图11～图16所示。

由图11～图16可知：2条基线的E方向和N方向差值不超过1 cm，第一条U方向差值不超过2 cm，第二条U方向差值绝大部分在2 cm以内；第一条基线观测条件较好，3个方向差值变化平稳，第二条基线流动站卫星几何构型变差或由于流动站观测值残余电离层延迟误差增大影响，3个方向差值变化跳动剧烈；将Ratio阈值设置为3[10]，小于3认为未固定，第一条基线一共处理7 200个历元，Ratio值小于阈值的有77个历元，单历元固定率为98.93 %，Ratio值大于3时固定成功率为99.99 %，第二条基线处理3 600个历元，Ratio值小于阈值的有37个历元，单历元固定率98.97 %，Ratio值大于3时固定成功率为99.99 %。由此可见第二个超宽巷组合(1，2，-3)在短基线情况下，解算成功率较高，在观测环境变差时，观测结果仍达到常规RTK的测量精度。为了便于分析，将2条基线的各个方向偏差值的均方根(root mean square，RMS)值列于表3，2条基线的E方向RMS值最小，其次为N方向，U方向RMS值最大，随着基线距离的增加U方向RMS值增加较快。

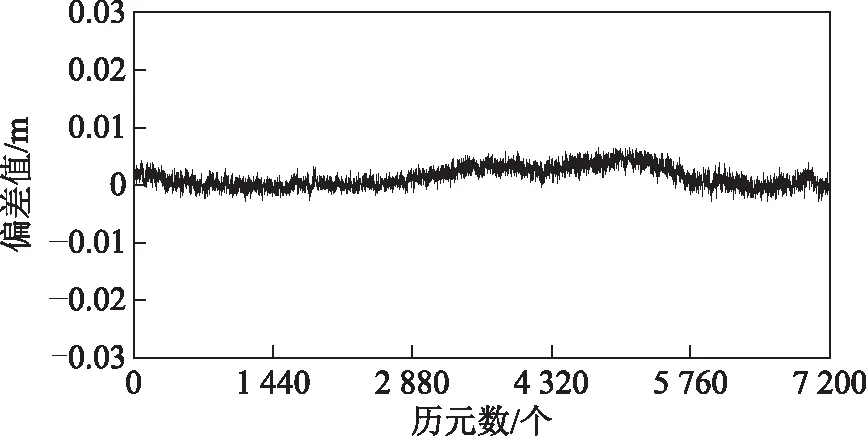
图12 50 m超短基线N方向差值

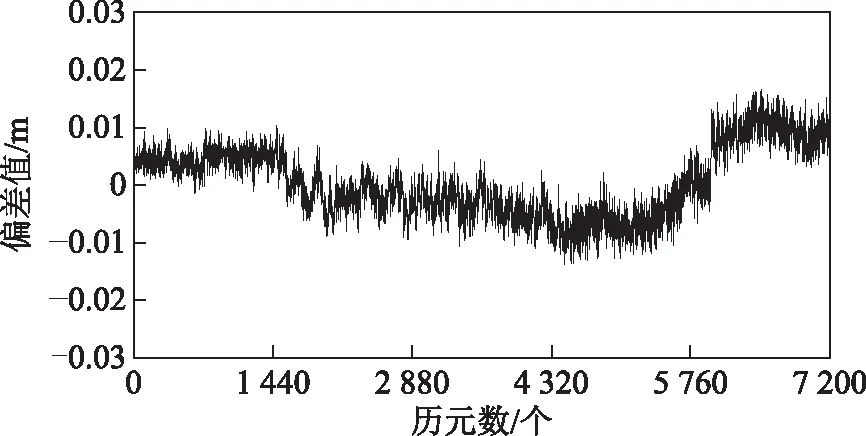
图13 50 m超短基线U方向差值

图14 7 km短基线E方向差值

图15 7 km短基线N方向差值

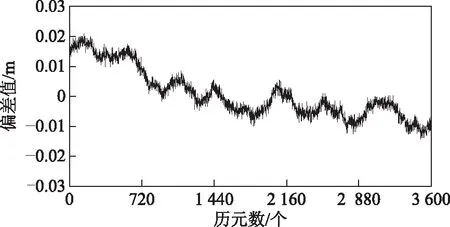
图16 7 km短基线U方向差值

表3 解算结果定位误差RMS值 m

4 结束语

本文利用2组实测数据进行分析，以参考站非差误差改正数的形式对流动站进行单颗卫星观测值的误差改正，改正后的流动站单历元解算2个超宽巷组合模糊度。短基线情况下，2个超宽巷模糊度解算成功率均接近100 %，超宽巷模糊度线性组合后得到宽巷模糊度对基本频点模糊度的求解构成约束，使得单历元基本频点解算成功率大大提高，定位精度达到厘米级。与现有BDS双差短基线RTK定位精度相当，能够满足测量精度要求。随着基线长度的增加，基准站与流动站大气误差相关性的降低会制约常规RTK的作业范围，电离层与对流层延迟等误差的处理直接影响流动站定位的可用性与精度，窄巷模糊度解算受残余电离层误差影响较大，中长距离难以瞬时固定，大气误差的快速分离将成为下一步研究的内容。