严格α2对角占优M矩阵A的估计式的改进

周 平

(文山学院数学学院， 云南 文山 663099)

引 言

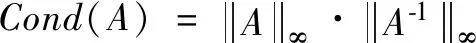
(1)

其中

2016年，在文献[15]中给出了优于式(1)的结果：

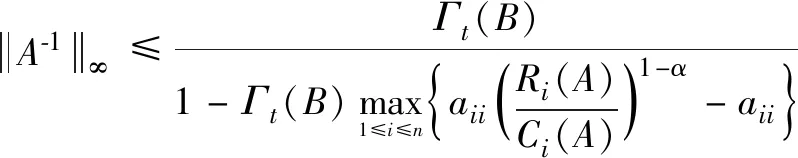
(2)

其中

1 符号、定义和引理

为了便于后文的探讨，先给出如下记号：

记N={1,2,…,n}，Rn×n是全体n×n阶实矩阵构成的集合.设A=(aij)∈Rn×n，对任意的i,j,k∈N，j≠i，令

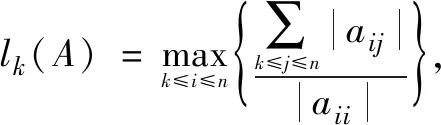
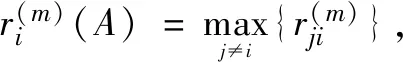
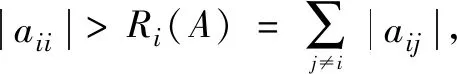
定义2[2]设A=(aij)∈Rn×n，如果A的所有元素aij≥0，那么A就叫做非负矩阵，记为A≥0。

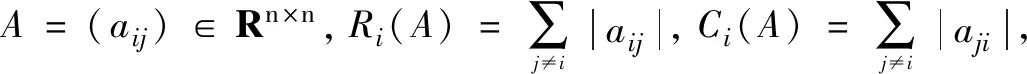
如果存在α∈[0,1]，致使A中的元素满足|aii|>Ri(A)αCi(A)1-α，i∈N，则A就叫做严格α2对角占优矩阵。

引理1[5]设A=(aij)∈Rn×n为严格对角占优M矩阵，则

引理2[10]设A,B∈Rn×n,A,A-B非奇异，则有

(A-B)-1=A-1+A-1B(I-A-1B)-1A-1。

2 主要结果

下面应用文中第一部分给出的引理和矩阵分裂的技术给出严格α2对角占优M矩阵的逆矩阵无穷范数的新估计式，进而获得其最小奇异值的估计式。

定理1设A=(aij)∈Rn×n是严格α2对角占优M矩阵,α∈(0,1],如果

N1={i∈N:Ri(A)>Ci(A)}≠φ

证明令矩阵A=B-F，这里B=(bij)∈Rn×n是SDD矩阵，F=diag(fij)∈Rn×n且是非负的，其中

由于A为严格α2对角占优M矩阵，所以有

|aii|>Ri(A)αCi(A)1-α=

近年来，由于草莓果酱、果酒等加工品的出现，使得草莓不仅限于鲜食，亦倾向于果品加工。草莓在温暖的天气中生长较快，因此大部分地区，都有草莓的栽培。但传统的栽培技术草莓的产量较低，尤其是北方地区，冬季的气温较低，草莓无法继续生长，若采用设施栽培等保护地的方式，草莓一直生长在适宜的环境中，能提高草莓的产量，笔者简述了丰产栽培技术，以期为草莓的丰产种植提供参考。

Ri(A)·Ri(A)α-1Ci(A)1-α=

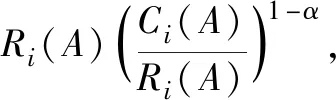
当i∈N1时，

当i∉N1时，

Ri(A)=Ri(B)

从而由定义1知，矩阵B是严格对角占优M矩阵。

进而结合引理2和引理3知

证明由文[16]中的定理2.1知

则

即

同理可证

从而ζ(B)≤κ，进而有

故该定理结论成立。证毕。

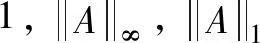
推论1设A=(aij)∈Rn×n是严格α2对角占优M矩阵,α∈(0,1],如果

N1={i∈N:Ri(A)>Ci(A)}≠φ

推论2设A=(aij)∈Rn×n是严格α2对角占优M矩阵,α∈(0,1],如果

N1={i∈N:Ri(A)>Ci(A)}≠φ

由于本文给出的定理1与文献[15]中的定理2不便于从理论上作比较，但可从下面的例子发现文中定理1的结果优于文献[15]给出的结果，在一定程度上提高了估计的精确度。

3 数值算例

由A中的元素知|a6,6|=R6(A)=38，当取α=0.95时，根据定义1和定义3知，A为严格α2对角占优M矩阵，下面把矩阵A分裂为A=B-F的形式，其中