灰色系统动态模型群GM(1,1)在秦淮河水质预测中的应用

胡祉冰，逄 勇，宋为威，邵咏絮

(1. 河海大学浅水湖泊综合治理与资源开发教育部重点实验室，南京 210098；2. 河海大学环境学院，南京 210098；3. 河海大学水文水资源学院，南京 210098)

1 前 言

在区域水环境影响评价及管理中, 水质预测是一项重要技术[1]。水质预测是在多元监测数据和水质参数变化之间建立相应的映射关系。这种映射关系的建立主要有两大类方法: 一是建立显式的方法，如概率法、多元回归法和指数法等；二是建立隐式的方法，如神经网络法、群体智能算法等[2]。按照所依据的理论基础不同, 水质预测模式大致可以归纳为5类：数理统计预测方法、灰色系统理论预测方法、神经网络模型预测方法、水质模拟模型预测方法和混沌理论预测方法。数理统计预测方法主要有单因素预测(平滑法[3]、时间序列法[4])和多因素预测(多元线性回归[5]、逐步聚类分析[6]、逐步回归分析[7])。灰色系统理论预测方法使用较多的是GM(1,1)灰色模型[8-9]。灰色系统动态模型预测是一种含不确定因素的系统进行预测的方法，是对既含已知信息和未知信息的系统预测。张保祥[10]运用灰色动态模型群法对济南市工业取水量进行了中长期预测；袁娜[11]基于灰色动态模型群理论对济宁市需水量进行预测；王韶伟[12]运用灰色动态模型群对福建省泉州市用水量变化趋势进行了预测分析；曾光明[13]运用灰色动态模型分析、预测焦作市人类-环境系统；郭锐[14]应用灰色系统动态模型群对泾河流域减沙效益进行了分析；李强[15]应用灰色动态模型预测了湖泊TN、TP的贮蓄量。前人研究的对象主要有工业用水量、济宁市需水量、泉州市用水量、人类环境系统、减沙效益及湖泊的TP、TN。而本文在前人研究的基础上对河道的高锰酸盐指数进行预测，以长江三角洲经济带典型大型城市-南京市为例，对南京市最大流域性河流秦淮河1/2源头句容河难达标高锰酸盐指数进行分析。基于2011～2016年高锰酸盐指数浓度，运用灰色系统动态模型群GM(1,1)理论，预测2017年水质，并与实际水质对照。本文为河道的水质预测提供了科学方法，可为类似研究提供参考，同时也对水环境管理具有一定的指导意义。

2 灰色系统动态模型建立

对于给定的原始时间序列{x(0)(t)}，t=1,2,3…,n，累加后得到新的数据系列为:

x(1)在上述方程中a和u为待识别参数，将上式离散化，得

△(1)(x(1)(t+1))+az(1)(x(t+1))=u

在(t+1)时刻的累减序列为:△(1)(x(1)(t+1))

△(1)(x(1)(t+1))=△(0)(x(1)(t+1))-△(0)(x(r)(t+1))=x(1)(t+1)-x(1)t=x(0)(t+1)

(k+1)时刻的背景值为z(1)(x(t+1)):

z(1)(x(t+1))=(x(1)(t+1)+x(1)t)/2

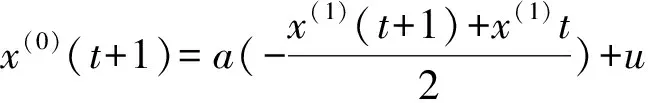
展开得

Y=B

运用最小二乘法进行求解，得

则其离散解为

还原到原始数据为

3 灰色系统动态模型群建立

根据灰色系统动态模型理论，要求建模采用的数据系列x(0)(t)中的数目应不少于4个。假定原始数据系列x(0)(t)中有n个数(n≥4),按照时间序列且含有原始数据系列中最后一位数的组合共有n-3组，按照时间序列建立n-3种子模型，形成灰色系统动态模型群。针对水质数据的离散性和无规律性，为了提高水质预测的精确性，采用光滑处理和累加结合的方法进行处理。

原始数据的光滑处理。对G(0)(t)随时间变化的水质数据，采用自然对数变换对原始数据光滑处理，得到X(0)

G(0)=(G(0)(1),G(0)(2)，…,G(0)(n))

x(0)=lnG(0)(t)

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

按照离散解：

第1个GM(1,1)子模型为

第2个GM(1,1)子模型为

……

第n-3个GM(1,1)子模型为

由n-3个GM(1,1)子模型建立灰色系统动态模型群。

则各个子模型预测值的算数平均值为最终预测结果

4 以南京市秦淮河高锰酸盐指数评价为例

以南京市秦淮河高锰酸盐指数评价为例，对南京市最大流域性河流秦淮河1/2源头句容河难达标高锰酸盐指数进行分析，基于2011～2016年高锰酸盐指数浓度，运用灰色系统动态模型群GM(1,1)理论，预测2017年水质，并与实际水质对照。其中2011～2016年句容河高锰酸盐指数浓度见表1。

表1 2011～2016句容河高锰酸盐指数实测浓度Tab.1 2011～2016 Jurong River Permanganate Index measured concentrations (mg/L)

4.1 对原始数据光滑处理

对表1所列的13组数据中，将2017年高锰酸盐指数浓度作为检验值。采用自然对数变换方式对其余12组实测数据光滑处理

G(0)(t)=(6.10,6.93,5.77,6.53,6.53,7.47,7.00,5.63,6.60,5.17,53.57,5.90)

X(0)=(1.81,1.94,1.75,1.88,1.88,2.01,1.95,1.73,1.89,1.64,1.72,1.77)

4.2 建立灰色系统动态模型群

根据GM(1,1)子模型理论，12组数据可建立8个灰色子模型，见表2所列。

表2 灰色系统动态模型群及其检验结果Tab.2 Grey system dynamic model group and its test results

4.3 模型验证

分别计算了各模型后验差C和小误差概率P，并进行模型验证，验证结果如表2所示。从验证结果可以看出，各个子模型均能较好满足预测的要求。

4.4 高锰酸盐指数浓度的预测

用这8个灰色系统动态子模型对2017年上半年的氨氮浓度进行了预测。经过数据还原，得到统计值的平均值为6.24 mg/L。2017年上半年的实测值为6.17 mg/L，相对误差为1.24%。一般的GM(1,1)预测模计算结果为7.09mg/L，相对误差为14.91%，而运用灰色动态模型群则误差下降13.67%。利用灰色系统动态模型群对2011～2017年秦淮河高锰酸盐指数浓度进行拟合和预测之后结果见表3。

表3 2011～2016句容河高锰酸盐指数模型群预测浓度Tab.3 2011～2016 Jurong river permanganate index model group predicted concentration (mg/L)

运用表2中子模型对2017年上半年水质进行预测。得到2017下半年～2019上半年句容河高锰酸盐指数模型群预测浓度为5.52 mg/L、5.45 mg/L、5.40 mg/L、5.35 mg/L，拟合与预测曲线见下图。从结果可以看出，灰色系统动态群法预测精准程度令人满意。

图 高锰酸盐指数浓度变化曲线Fig. Permanganate index concentration curve

5 结 语

灰色系统模型对数据资料的丰富程度较低，但是仅由单一的子模型预测难以获得较为理想的结果。本文针对南京市最大流域性河流秦淮河1/2源头句容河难达标高锰酸盐指数进行分析，运用灰色系统模型理论，建立了8个灰色系统动态子模型，形成灰色系统动态模型群，减弱随机波动性带来的影响，增加数据光滑程度，提高模型预测精度。经过数据还原，得到统计值的平均值为6.24 mg/L，2017年上半年的实测值为6.17 mg/L，相对误差为1.24%。灰色系统动态模型群GM(1,1)可应用于南京市水质预测，对水环境管理具有指导意义。