Dynamical stable-jump-stable-jump picture in a non-periodically driven quantum relativistic kicked rotor system∗

Hsincheng Yu(于心澄),Zhongzhou Ren(任中洲),2,†,and Xin Zhang(张欣)

1 Department of Physics,Nanjing University,Nanjing 210008,China

2 School of Physics Science and Engineering,Tongji University,Shanghai 200092,China

Keywords:quantum chaos,dynamical localization,quantum resonance

1.Introduction

The kicked rotor model is an important chaos model in the study of nonlinear dynamics.It describes a rotor that is driven by a periodic potential.The dynamic evolution of the classical kicked rotor can be calculated by the“standard map”or“Chirikov map”.[1]In the classical kicked rotor model,an initial ensemble evolves as the kick times.The evolution of the average value of p2shows a chaotic classical diffusion.The dynamic evolution of the quantum kicked rotor model is described by the Floquet operator.In the quantum kicked rotor model,the dynamic localization of energy is found and the dynamic localization phenomenon is tentatively explained by an analogy with the Anderson localization phenomenon in the tight binding model.[2-13]Recently,interest has risen in the quantum relativistic kicked rotor(QRKR)model.Although it is similar to the quantum kicked rotor model,it has some unique characteristics.The most interesting characteristic of the QRKR is its quantum resonance phenomenon.If the quantum resonance condition is satis fied,then the QRKR system will show a superballistic transport characteristic.[14-18]

Studiesofthe QRKRmodelhave focused on periodic perturbations.It is intriguing to investigate whether the phenomena of dynamical localization and quantum resonance would still survive if the perturbations are not periodic. In this work,we intend to introduce a non-periodically driven QRKR model,which adds a small constant to the interval of kicks after each kick,T(n)=T(0)(1+n/d).Here 1/d is a small constant.We note that the non-periodically quantum kicked rotor(QKR)model has been studied in Ref.[19].The classical-like diffusion was demonstrated instead of the quantum dynamical localization.However,a new pattern is achieved here;i.e.,a stable-jump-stable-jump pattern.This might give an active response to the survival of the quantum resonance.

The rest of this article is arranged as follows.In Section 2,we review the framework of the one-dimensional quantum relativistic kicked rotor(QRKR)and introduce a nonperiodically driven QRKR model,which adds a small constant to the interval between kicks after each kick.In Section 3,we show our numerical results and do some quantitative analyses on the dynamical stable-jump-stable-jump picture.Finally,we give a summary in Section 4.

2.One-dimensional QRKR model

The one-dimensional QRKR model is derived by considering the Dirac Hamiltonian of a one-dimensional rotor in fluenced by a periodic delta-function potential[11,20,21]

In Eq.(1), σxand σzrepresent the Pauli-X matrix and the Pauli-Z matrix,respectively.I is a 2×2 unitary matrix.is the momentum operator distinguished from the angular momentum operator,parameter c is the speed of light,parameter k is the kicking strength,parameter m is the mass of the kicked rotor,and parameter R is the radius of the onedimensional ring.Parameter q is a parameter associated with the period in angular position.In order to simplify calculations,we take the convention c=¯h=R=1 and some parameters are defined as follows:[21]

We define the angular momentum operator=.The Hamiltonian of the quantum relativistic kicked rotor(QRKR)in dimensionless units[21]is given as

where α,M,K,and q are parameters.t′=t/T,where T is the interval between kicks.is the angular position operator.The Hamiltonian describes a spin-1/2 particle confined to a one-dimensional ring and kicked by a potential which is a cosine function in the angular position.This system is similar to the two-level system.The solution space can be regarded as a Bloch sphere product the angular momentum space or the angular position space.[21]For a vanishing M,this model reduces to the Maryland model.

In our calculations,we have chosen a “spin-down”state as the initial state.This is given as

where m is a sufficiently large integer and the angular momentumcan only take integers.

The dynamical evolution equation of the one-dimensional QRKR is written as

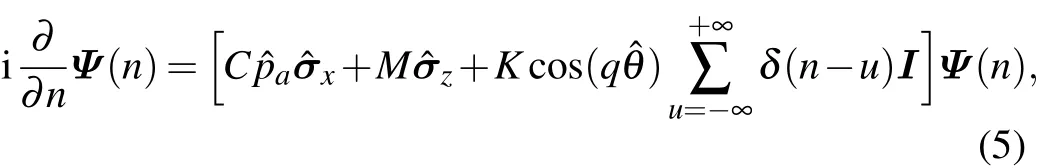
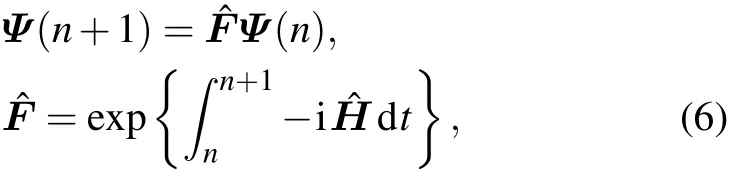
The evolution calculation is carried out by splittinginto two parts,and.Those two operators are,respectively,diagonal in the angular momentum representation and the angular position representation.First,we perform discrete Fourier transformation on the wave function in the angular momentum representation and let e-iKcos(qˆθ)Ioperates on it.Second,we perform the inverse Fourier transformation on the wave function in the angular position representation to get wave function in the angular momentum representation again.Finally,we operate e-i(Cˆpaˆσx+Mˆσz)on it.We have operated anoperator on the initial wave-function.The next work is to ensure that we have enough repetitions ofIn our numerical simulations,we use the fast Fourier transformation algorithm to finish the discrete Fourier transformation and inverse Fourier transformation.[18,21]

In this paper,we consider a non-periodically driven QRKR model which adds a small constant to the interval of kicks after each kick

where parameter n represents the kicked time.1/d is a constant parameter.C(n),M(n),and K(n)are variables of the kick times,which are given as

Then,the quantum states of different kicking numbers are related by

Then we have

3.Numerical results and analysis

In this section,we show our numerical results of the nonperiodically driven QRKR.Our results can be explained explicitly with the quantum resonance phenomena.

In Fig.1,we compare the momentum spreading with different increasing rates d=104,106,1020.From this figure,we find that the initial amplitude of oscillation is relatively large.Furthermore,as the kicked times increase,the initial amplitude of oscillation decreases.If d approaches in finity,our results reduce to the results shown in Ref.[18].

Fig.1.This figure shows the momentum spread with kicked times.We set the initial wave-function as a spin-down state.This shows a Gaussian distribution in angular momentum space centered at p=0.We take M(0)=6,C(0)=2π/3+0.01,K(0)=0.8,q=3,σp=4,σp is the standard deviation.These quantities are given in dimensionless units.

As can be seen in Fig.2,the evolution of momentum spreading follows a stable-jump-stable-jump pattern.The momentum spreading remains approximately constant for a while and it then jumps upward or downward,it then settles on a different constant value.The interval between these“jumps”is essentially a constant for different values of d.We find that the interval between the jumps is linearly proportional to d.Approximately,the interval between jumps divided by d is a constant.which is 1/4 as shown in Fig.2.Since the parameters we set in the calculation are M(0)=6,C(0)=2π(4/3),K(0)=0.8,q=3,σp=4.We find the relation that 1/4=2π/(C(0)·q).With this relation,the interval between jumps has the relation given below,

where Δ represents the interval between jumps.To derive this equation through the quantum resonance condition of QRKR model,we rewrite the quantum resonance condition of QRKR model mentioned in Ref.[17]

This indicates that if α is an integer divided by a factor of q,the quantum resonance will happen.Here r,s,and n are all integers.We define the “the general reciprocal”as follows.The general reciprocal of q means that this number is generated by some positive integer times 1/q.In terms of our definition,all of α(0)are the general reciprocal of q.The minimal is 1/q.So we have

where t1and t2represent the number of kicks;n1and n2are some integers.Then,one obtains

which is exactly Eq.(11).This suggests that these leakages are caused by the quantum resonance phenomenon.

Fig.2.We increase the kick time to show the stable-jump-stable-jump picture.The initial wave-function takes a spin-down state.This shows a Gaussian distribution in angular momentum space centered at p=0.M(0)=6,C(0)=2π(4/3),q=3,σp=4.Panels(a)and(b)show the weak kicked case(k=0.8)and the strong kicked case(k=6),respectively.

Fig.3.The initial wave-function takes a spin-down state.It shows a Gaussian distribution in angular momentum space centered at p=0.We take M(0)=6,K(0)=0.8,q=4,σp=4,d=1000.These quantities are given in dimensionless units.

It is also of interest to study the situation when the initial kicking interval does not satisfy the quantum resonance condition.In Fig.3,we reset the parameters so that the quantum resonance condition is not satis fied initially,while the momentum spreading will be localized in the low momentum area until the first quantum resonance condition is satis fied.Then,it will hop to a high energy area and exhibits the characteristics that we have discussed previously.Furthermore,we increase the interval of kicks randomly.Even in this situation,we find that the stable-jump-stable-jump pattern still exists.This suggests that the quantum resonance is independent of the periodic perturbation.

In Fig.4,we show an example of the wave-packet spreading in the angular momentum space.The initial wave-function takes a spin-down state and shows a Gaussian distribution in angular momentum space centered at p=0.As the kick time increases,the symmetric wave-packet spreading becomes increasingly significant.

4.Conclusion

We study a special one-dimensional non-periodically driven QRKR model based on the methods in Refs.[18]and[21].This one-dimensional non-periodically driven QRKR is found to show a stable-jump-stable-jump pattern.This phenomenon can be understood by the quantum resonance.We also find thatthe momentum spreading ofkicked rotorpresents a transport behavior when the quantum resonance condition is satis fied.If the quantum resonance condition is not fulfilled,then the momentum spreading will tend to a confined evolution.We compare our results with the results in the similar non-periodically driven QKR system[19]and conclude that the dynamical evolution of the non-periodically driven QRKR system is dramatically different from that of the nonperiodically driven QKR system.