基于最优化线抽样法的XAPR自然循环功能失效研究与分析

王宝生，唐秀欢，包利红，朱 磊

(西北核技术研究所，陕西 西安 710024)

西安脉冲堆(XAPR)作为池式研究堆，具有停堆后的非能动安全性，即当反应堆发生事故时，依靠堆池水的自然循环冷却将堆芯余热非能动安全导出。然而这样的B型非能动系统[1]在缓解严重事故时，易受到不确定性的影响，从而引起系统的功能失效[2]。因此，有必要对XAPR自然循环功能失效进行研究与分析，并发展一种评价其失效概率的方法，为XAPR概率安全评价提供重要的信息。

研究表明，功能失效概率的计算可采用响应面(RS)法、一次二阶矩法(FOSM)、直接蒙特卡罗(DMCS)法、自适应蒙特卡罗(AMCS)法、自适应重要抽样(AIS)法和重要抽样蒙特卡罗(ISMCS)法等[3-8]。然而，RS法和FOSM能简化复杂模型的处理，但对于高非线性问题的精度不够理想；DMCS法能很好地模拟真实的概率，但需进行大量抽样，计算效率低下；各种改进的蒙特卡罗(MCS)法通过引入重要密度函数，可提高计算效率，但对隐式关系的热工水力过程，仍依赖响应面方程来替换热工水力程序，难以避免RS法的固有缺点。

本文提出一种重要方向最优化线抽样(OLS)法来评价XAPR自然循环功能的可靠性。基于自然循环系统功能可靠性[9-11]的评价内容及流程，考虑系统模型及输入参数的不确定性，利用OLS法获得输出响应的累积分布函数，进而计算功能失效概率及灵敏度系数。以XAPR自然循环冷却堆芯能力的可靠性评价为例，结合中破口失水事故，对功能失效进行评估，并与其他几种方法进行比较。

1 功能失效概率评估数学模型

假设影响系统功能可靠性的输入变量X=(x1,x2,…,xn)由n个不确定输入参数组成，那么功能失效概率Pf可由下式表示：

(1)

式中：g(X)=A-y(X)为功能函数，A为失效准则，y(X)为用函数映射关系表示的热工水力学程序，g(X)>0表示系统处于安全状态，g(X)<0表示系统处于失效状态，g(X)=0表示系统处于临界状态；fX(X)为输入变量X的联合概率密度函数。

为便于计算，式(1)可改写为如下形式：

(2)

式中：I[g(X)]为指示性函数，若g(X)<0，则I[g(X)]=1，若g(X)≥0，则I[g(X)]=0；Ω为整个积分区域。

对于复杂的自然循环系统，难以用快速积分的方法求解式(2)，因为g(X)是一个复杂的热工水力学程序，其功能函数都是模拟程序，需用数值方法求解。由于功能失效概率一般较小，采用MCS法计算需进行多次抽样，且每次抽样均要运行热工水力学程序，计算量非常大。针对这一问题，本文提出重要方向OLS法进行求解。

2 重要方向OLS法

2.1 线抽样法基本思想

该方法的基本原理是利用直线代替随机点确定出高维复杂系统的失效域，通过重要方向α上的插值和n-1维上的随机抽样来高效地实现失效概率的计算。图1示出线抽样法示意图。

(3)

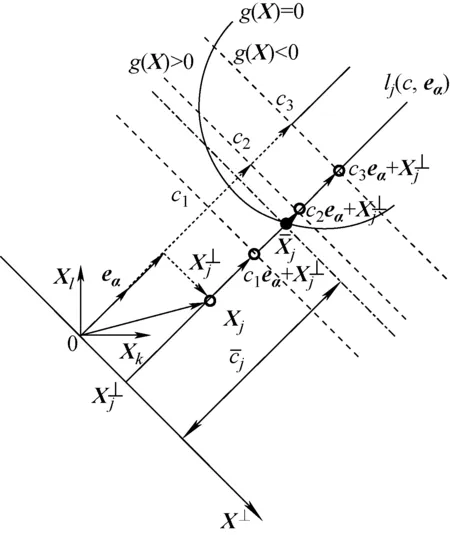
图1 线抽样法示意图Fig.1 Sketch map of line sampling method

(4)

(5)

2.2 最优化重要方向的确定

线抽样法的有效性取决于重要方向的选取，当重要方向与最优重要方向一致时，效率达到最佳。定义最优化重要方向αopt为使系统失效概率估算值方差最小的重要方向。那么最优化重要方向可表述为αopt=Xopt/‖Xopt‖，其中Xopt位于失效域内。以系统失效概率估算值方差最小为目标，构建如下所示具有约束条件的优化模型：

minM=Var[PN(F)]=σ2[PN(F)]

s.t.αopt=Xopt/‖Xopt‖

Xopt∈F,{g(Xopt)<0}

(6)

采用遗传算法对所建立的优化模型进行求解，其主要步骤如下。

1) 通过遗传算法模拟产生NT个条件样本点Xj(j=1,2,…,NT)，计算样本点的质心

2.3 OLS法实现过程

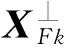
2.4 OLS法的适用范围

OLS法无需找到设计点，该方法只需确定失效域中的质心，即可通过遗传算法求解约束条件准确确定最优化重要方向，且采用3点二次插值在非线性情况下更易逼近真实的隐式功能函数方程。该方法不依赖于功能函数方程的显式表达，且在重要方向上具有极高的效率，因此该方法适用于非线性程度较高的大型复杂自然循环系统可靠性分析中的高维小功能失效概率问题，对于具有不规则极限状态曲面的功能函数，该方法尤其适用。此外，对于含有非正态随机变量的情况，需先将非正态随机变量转为标准正态变量，再运用该方法求解。

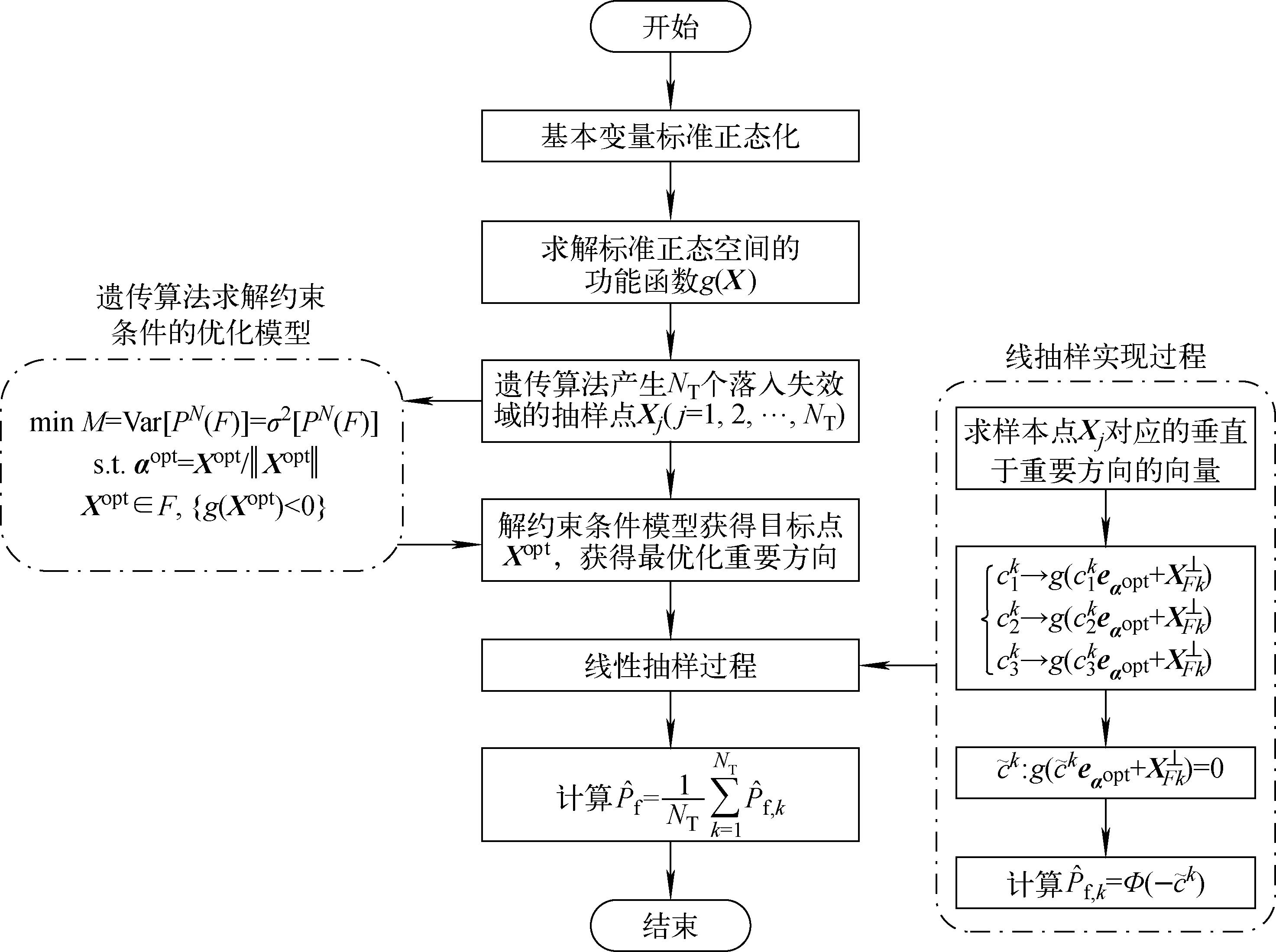
图2 OLS法的计算流程Fig.2 Flow chart of optimized line sampling method

3 OLS法的应用

以XAPR自然循环冷却堆芯能力的可靠性评价为例，考虑模型与输入参数的不确定性，对中破口失水事故下的自然循环功能失效概率进行量化分析。

3.1 系统安全功能

XAPR采用池式反应堆结构，堆芯采用自然循环冷却，当反应堆发生冷却剂丧失事故时，依靠池水自然循环冷却，或与环境的热量交换即可将堆芯余热非能动导出。当发生失水事故时，事故进程可划分为3个阶段：1) 水冷自然循环冷却阶段；2) 堆芯半裸露阶段；3) 空气冷却自然循环阶段。这样即可在失水事故时建立堆芯长期自然循环冷却，将堆芯余热导出，保证燃料元件的完整性。

3.2 系统模型与功能准则

采用RELAP5模拟失水事故堆芯自然循环冷却过程。XAPR热工水力建模计算节点示于图3。图3中控制体101～107为堆池，120～124为堆池混凝土壁外空气边界，150～163为一回路管道，170～172为简化二回路边界，109为堆池顶部空气边界。为验证模型的准确性，采用运行工况作为边界条件进行计算，得到堆芯自然循环流量为12.21 kg/s，该流量与实际自然循环流量12.13 kg/s基本一致。

定义功能准则为：当包壳温度低于或等于500 ℃时，燃料芯体最高温度应低于1 150 ℃；高于500 ℃时，应低于970 ℃。从概率安全角度出发，假设燃料芯体最高温度超过安全限值970 ℃则认为功能失效。设向量X为不确定性参数，To,max(X)为燃料芯体最高温度，则功能函数g(X)可表示为：g(X)=970-To,max(X)，当g(X)<0时，即认为功能失效。

3.3 系统不确定性参数

XAPR运行时涉及到2种不确定性：第1种是偶然不确定性，它与模型的几何性质有关；第2种是认知局限不确定性，它与运行和试验数据缺乏而导致对有关现象认知的局限性有关[2]。本文重点研究因认知局限的不确定性。

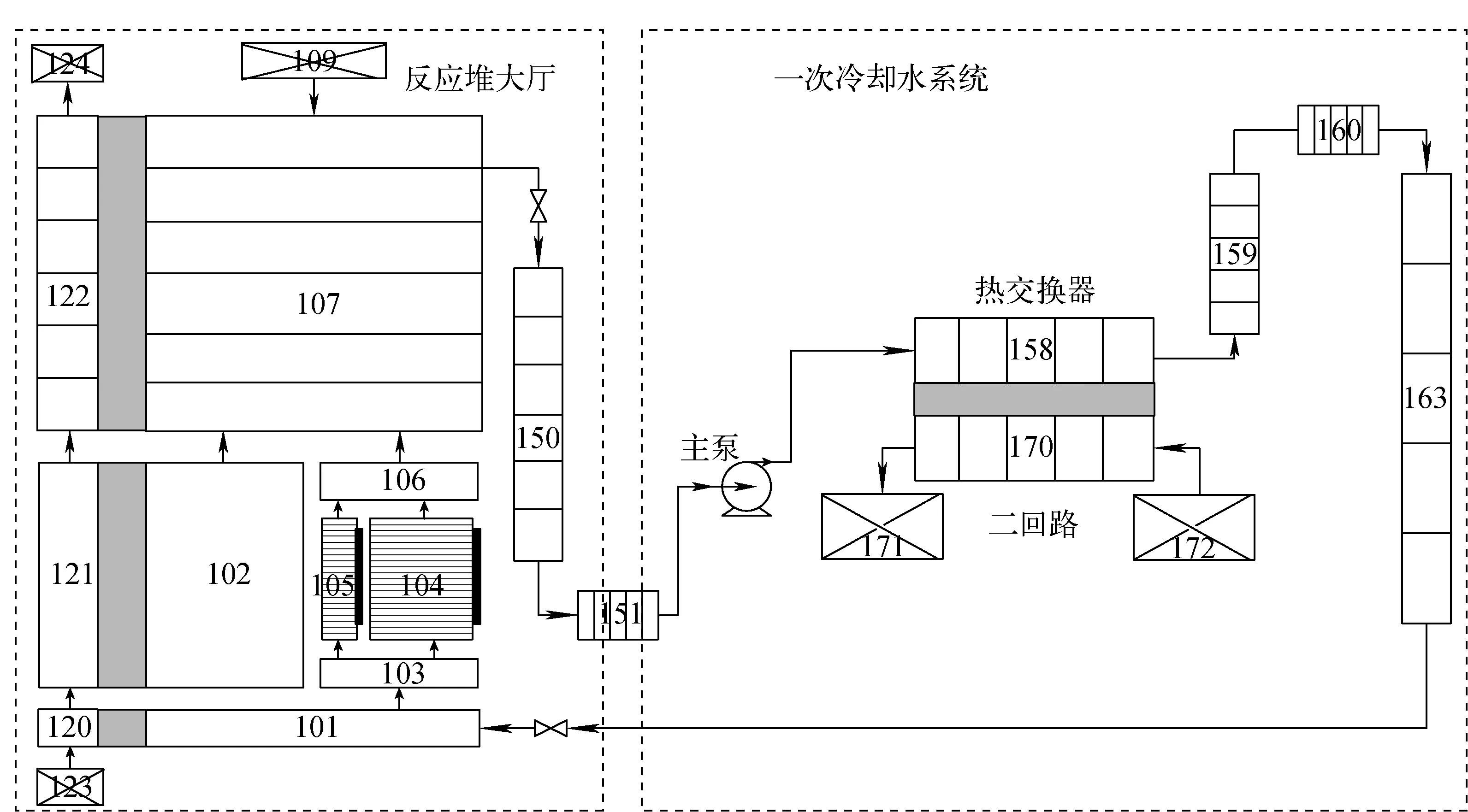
图3 RELAP5计算节点Fig.3 Nodalization of RELAP5 calculation

利用层次分析法及专家判断相结合的方式，识别出对XAPR堆芯自然循环影响较大的不确定性参数。在目前处理中，当可得到的数据有限时，各输入参数的概率分布及取值区间主要以工程设计标准为基础，并结合专家评价的主观方法得出。表1列出输入参数的概率分布及特征参数。这些参数的取值及分布考虑了所有可能的事故工况，是一种较为保守的方法。

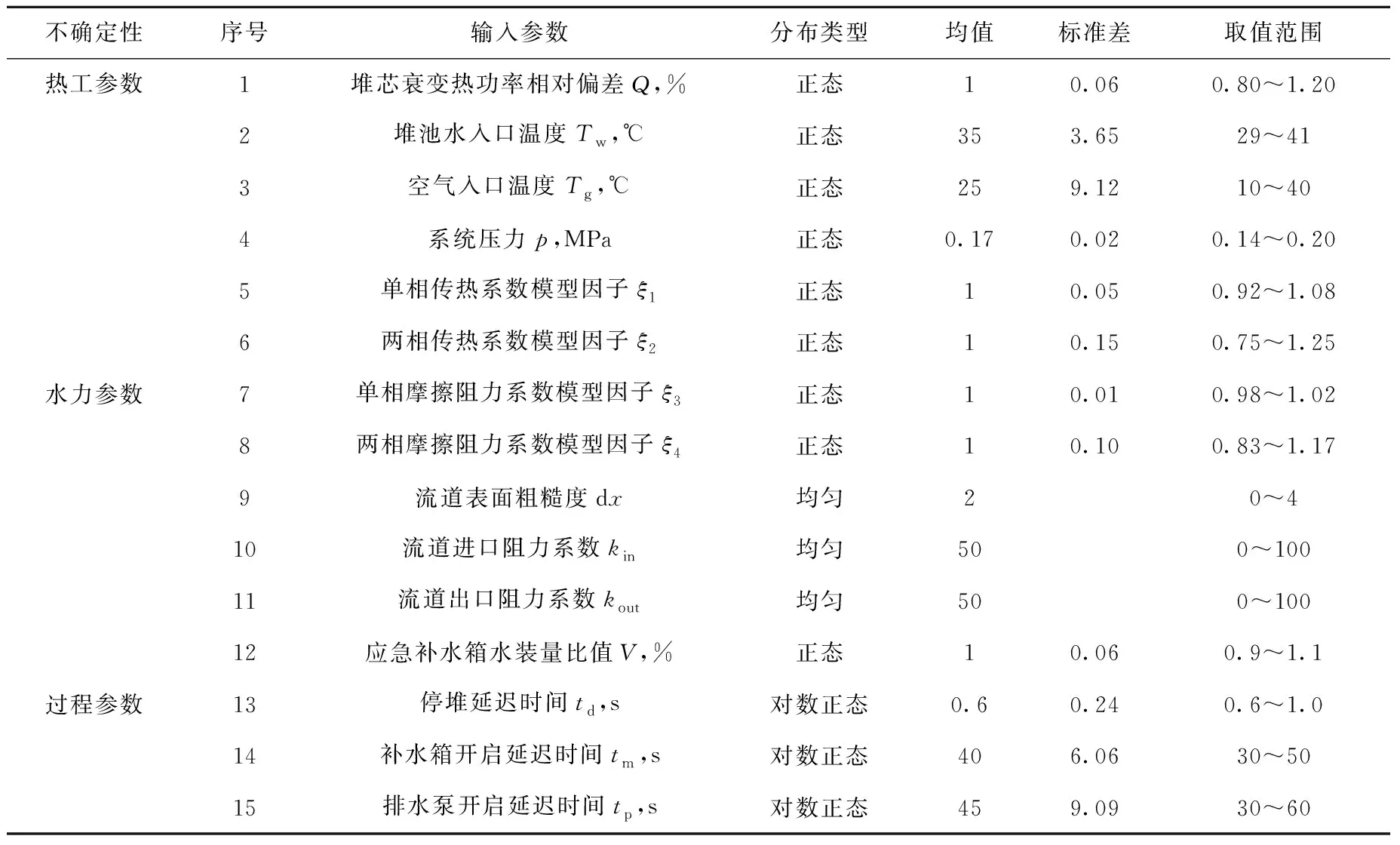
表1 输入参数的概率分布类型及特征参数Table 1 Probability distribution and characteristic parameter of input parameter

3.4 功能失效概率评估与结果分析

为便于比较，本文同时采用了DMCS、OLS、AMCS和AIS等方法进行计算。图4示出不同方法的功能失效概率随样本数的变化。由图4可见，当OLS法样本数增大至5 000后，失效概率几乎不再随NT的增加而波动，且计算结果即可达到DMCS法样本数为105时的计算精度(对于概率为10-3数量级，抽样105次对于置信水平99%能获得满意结果，因此以105次抽样结果作为基准值)[6]。同时从图4还可看出，当样本数分别达到50 000及20 000时，AMCS法和AIS法也能达到较好的收敛效果。因此，本文分别选取105、5 000、50 000、20 000作为DMCS、OLS、AMCS及AIS等方法的样本数。

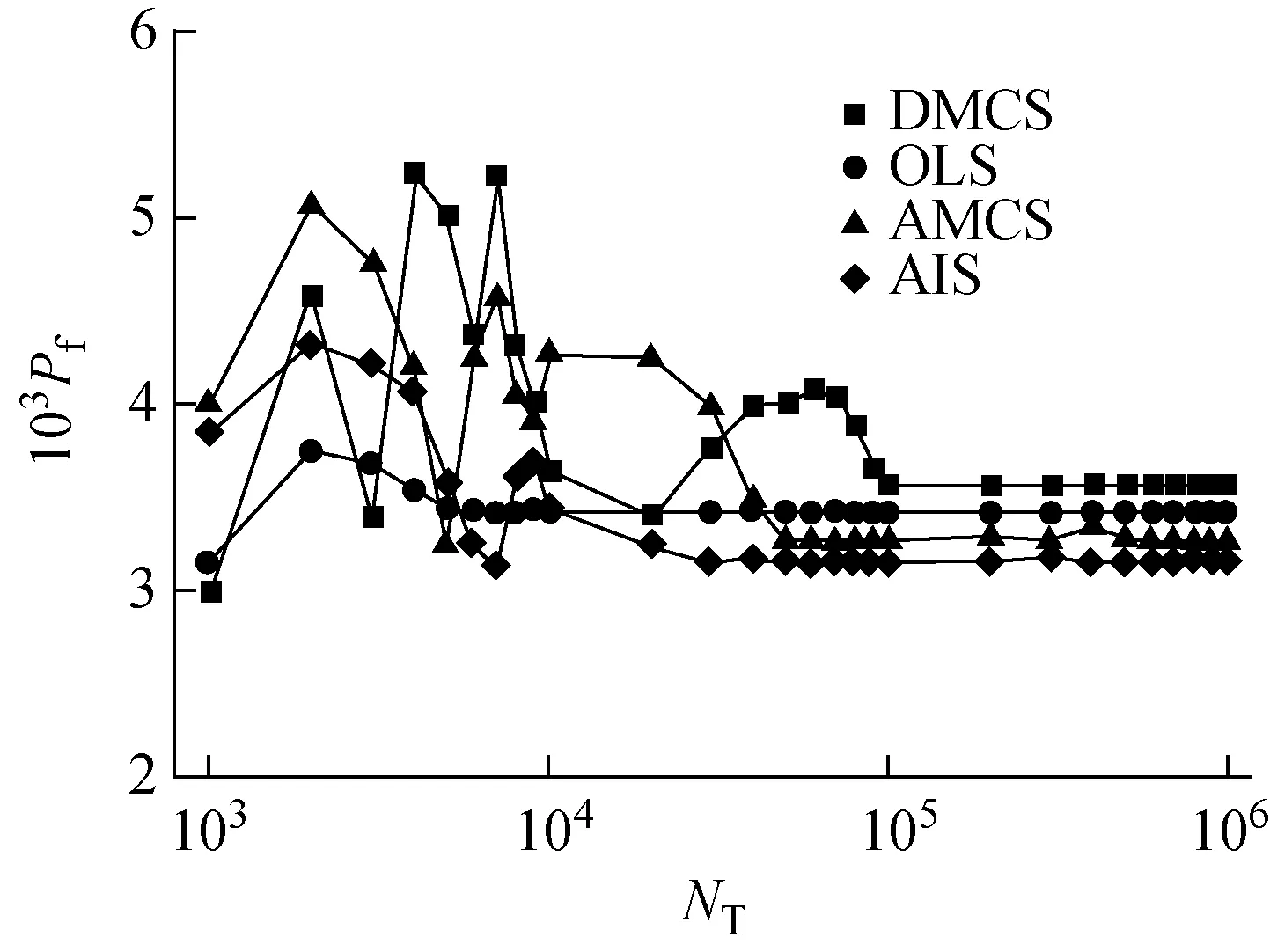
图4 失效概率随NT的变化Fig.4 Failure probability convergence with NT

图5示出4种不同方法得到的反映模型输出To,max不确定性的概率密度函数和累积分布函数。由图5可见：To,max近似服从正态分布；

OLS法抽样NT=5 000次的计算结果与DMCS法抽样NT=105次的基准值吻合较好，但样本数却少得多，约为DMCS法样本数的1/20。

为便于比较引入两个指标：相对误差ξ和单位变异系数Δ[8]：

(7)

(8)

式中，δ为变异系数。显然，单位变异系数Δ越小，计算效率越高；相对误差ξ越小，计算精度越高。不同方法计算得到的失效概率Pf、单位变异系数Δ、相对误差ξ和计算时间tcom分别列于表2。由表2可见：DMCS法存在抽样效率低、计算耗时的缺点，在抽样数NT=105时才能达到误差要求；RS法实质上是曲线拟合的近似方法，其计算精度依赖于功能函数的线性程度，对于功能函数非线性程度较高时计算结果偏差较大，本算例自然循环系统为非线性，所以结果欠佳；AMCS法和AIS法均属于重要抽样的蒙特卡罗方法，但对于隐式关系的热工水力过程，仍依赖RS法替代热工水力程序，无法避免RS法的缺点；OLS法的计算结果与基准值相近，具有较高计算效率的同时保持了良好的计算精度。更重要的是，该方法只需不确定性参数输入变量和对应热工水力程序的输出响应值，不依赖于功能函数的显式表达式。

3.5 参数灵敏度分析

灵敏度分析可反映输入参数的不确定性对系统功能可靠性的影响，并给出量化的重要度排序，从而为提高系统功能可靠性提供指导性建议，有效减小不确定性。由于非能动物理过程为隐式非线性关系，传统表征参数灵敏度的相关系数、标准回归系数、秩相关系数及标准秩回归系数等具有局限性[10]。本文将基本变量均值变化引起功能失效概率变化的比率表征为灵敏度，在数学上由失效概率Pf对基本变量均值μx的偏导数予以表达，即∂Pf/∂μx。为消除量纲影响，引入了无量纲灵敏度系数Sμxi=(∂Pf/∂μxi)×(σxi/Pf)[12]。灵敏度分析结果如图6所示。

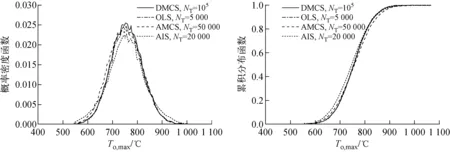
图5 To,max的不确定性Fig.5 Uncertainty of To,max

计算方法NT103PfΔξ/%tcom/hDMCS1053.48017.0901 002.8RS1573.1973.238.13159.8AMCS+RS50 0003.12510.1710.20687.4AIS+RS20 0003.0574.1312.16365.3OLS5 0003.4051.682.15127.8

由图6可见，衰变热功率相对偏差Q、空气入口温度Tg、流道进口阻力系数kin、流道出口阻力系数kout、排水泵开启延迟时间tp对系统输出有较大影响，其中Q、Tg和tp最为敏感。因为这些参数直接影响事故发生后自然循环的输热能力和建立的时间，对自然循环余热排出功能可靠性影响较大。因此，减小上述影响较大的输入参数的不确定性可有效降低自然循环的失效概率，提高系统的功能可靠性。

选取Q、Tw、Tg、ξ2、ξ4、kin、kout、tm及tp等9个参数作为关键参数，其余6个参数采用均值保持不变。这样15个输入参数的模型可变为9个输入参数，大幅简化了模型。对简化模型分别采用DMCS法和OLS法进行计算，与初始模型的结果进行比对，结果列于表3(50次计算的统计结果)。由表3可知，当考虑9个关键参数时，DMCS法和OLS法计算的失效概率均值分别为3.401×10-3及3.359×10-3，很接近初始模型的计算均值，但其计算效率更高、计算时间更少。

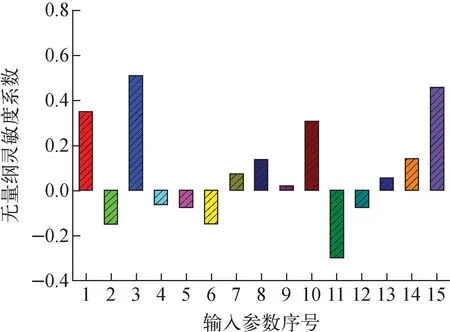
图6 输入参数归一化灵敏度系数Fig.6 Normalized sensitivity coeffcient of input parameter

计算方法NT初始模型简化模型1)失效概率均值标准差Δtcom/h失效概率均值标准差Δtcom/hDMCS1053.484×10-31.892×10-417.171 002.53.401×10-31.061×10-410.06701.9OLS5 0003.409×10-37.854×10-51.64127.93.359×10-35.117×10-51.2176.7OLS2)5 0001.042×10-42.076×10-61.1460.1

注：1) 9个关键参数模型

2) 忽略9个关键参数模型

4 结论

1) 本文采用遗传算法求解具有约束条件的优化模型，找出最优化重要方向，并将失效域的条件样本用作随机样本，使得计算效率大为提高。相比于其他方法，该方法具有较高的抽样效率和计算精度，且该方法只需基本变量和对应的功能函数输出值，不依赖功能函数的显式表达式，对于隐式关系具有较强的适应性。

2) XAPR破口失水事故时，不确定性导致的功能失效总是有非零的发生概率，其失效概率为3.480×10-3。在涉及XAPR自然循环的可靠性评估中，功能失效是重要的，其失效概率应基于热工水力计算和概率论方法进行全面评价。

3) 减小Q、Tg、kin、kout及tp等5个关键参数的不确定性，可更有效地降低自然循环的失效概率，提高XAPR自然循环冷却堆芯的能力。同时，通过灵敏度分析将模型简化后，计算量大幅减少，但计算结果仍很接近。