离散纵标六角形节块法及CMFD加速研究
李志勇
(中广核研究院有限公司,广东 深圳 518031)
中子输运方程的求解方法有很多,如碰撞概率方法、穿透概率方法、MOC方法以及离散纵标法[1-5],其中,离散纵标法得到了非常广泛的研究和应用。对于离散纵标法的求解大多采用差分方法[6],对于方形几何问题,Lawrence等[7]通过对堆芯扩散节块格林函数方法的扩展,提出了一种两维离散纵标节块法即离散节块输运法(DNTM)。李志勇[8]提出了一种基于中子平衡形式的离散纵标节块法及相应的粗网有限差分(CMFD)加速技术,并取得了很好的效果。DNTM相对于差分方法,在相同的精度要求下大幅减少了计算时间,因此DNTM是一种很有价值的方法。
对于六角形几何,Ikeda等[9]提出了一种离散纵标节块法并在快堆问题中得到了应用。本文基于该方法并结合方形几何下的中子平衡形式的离散纵标法,将中子平衡形式的离散纵标法推广到六角形几何,得到六角形几何下的中子平衡离散纵标节块法,使得离散纵标节块法更为简洁和有效,也使其易于采用在堆芯扩散节块方法上广泛应用的一些加速技术。
六角形几何下的中子平衡离散纵标节块法收敛速度较慢、计算较为耗时,因此本文同时提出六角形几何离散纵标节块法下的CMFD加速计算方法。
1 理论模型
1.1 基本方程[9]
微分形式的六角形中子输运方程可写为如下形式:
(1)
(2)

图1示出六角形节块横向积分示意图。通过类似于堆芯扩散节块法的横向积分技术在区间-ys(x) (3) (4) (5) 图1 六角形节块横向积分示意图Fig.1 Transverse integrate sketch of hexagonal node 横向积分角中子通量可直接求解如下。对于μm>0,有如下的关系: (6) 另外,还需对标量中子通量和中子源分布采用类似于节块法的多项式展开,有: (7) (8) 其中,hi(x)={1,x,x2-5/72},hi(x)的选取为了便于高阶角中子通量的求解需满足相对于权重函数ys(x)正交的要求,即: (9) 其中,δij为克罗内克函数。 对于横向泄漏,这里对左右半节块均采用平坦泄漏近似,这对于求解六角形组件栅元输运问题应该是合适的。根据横向积分节块面平均角中子通量以及节块标量中子通量,构造成一般的源迭代形式,即可完成离散纵标六角形节块法的求解,具体过程可参考文献[9]。 根据横向积分离散纵标方程(式(3)~(5))可求解出节块表面横向积分面平均角中子通量,这里采用文献[9]的方法,横向积分出射面平均角中子通量为: (10) (11) (12) 将对横向积分中子源和横向中子泄漏的近似代入式(10),可得到出射横向积分出射面平均角中子通量的具体形式: (13) (14) (15) (16) CL(-μm)=CR(μm),CR(-μm)=CL(μm) (17) 注意到对任意角度方向的离散纵标中子输运方程(式(1)、(2))进行面积积分(高斯积分),可得到两维笛卡尔坐标下的任意角度方向中子平衡方程,这与堆芯扩散节块法的过程类似。对于六角形中子输运离散纵标方程,其形式可表示为: (18) 离散纵标节块法可在较粗的网格下获得较高的计算精度,但由于中子输运方程需显式求解角中子通量,整个数值计算过程需更多的源迭代从而消耗较多计算时间,因此研究和采用有效的加速技术对于离散纵标节块法是很有必要的。CMFD加速技术在堆芯扩散程序中得到应用,且在方形离散纵标节块法中,CMFD技术的加速效果非常优良[8]。 CMFD加速中子输运方程求解的基本思想是基于扩散方程有限差分形式,根据输运求解得到面中子流和体积平均通量的关系,来修正在有限差分扩散方程中的等效扩散系数,最终使得输运方程中子流与CMFD中子流相同从而两者等价。在这一过程中利用CMFD的快速计算能力,计算得到等价问题的中子通量和本征值并修正输运方程中子通量以获得加速的效果。本文采用的中子离散纵标六角形节块法CMFD加速技术理论模型如下。 (19) (20) (21) s=x,u,v (22) 将式(21)、(22)代入到中子扩散平衡方程就可得到一般的CMFD迭代方程(式(23)),对其采用一般的源迭代求解就可得到本征值和中子通量,随后将其作为SN的初始本征值和标量中子通量重新进行SN外迭代以实现加速目的。 (23) 本文采用文献[10]中提出的1个组件问题作为参考问题。该组件问题由五环栅元构成,栅元栅距为1.732 05 cm(即六角形栅元边长为1 cm),组件外边界条件为镜面反射条件。该问题分为两种情况,一个是两群单区问题,即全部栅元均为燃料栅元;另一个是两群两区问题,组件最外圈全部为轻水栅元,其余位置处为燃料栅元。图2给出该基准问题的几何结构(1/6对称图),表1列出栅元材料中子截面。 图2 参考问题的1/6组件几何结构Fig.2 Reference problem 1/6 assembly layout 本文采用1个栅元作为1个节块进行计算,并对角中子通量采用36个对称方向进行计算。 表1 参考问题中子截面Table 1 Reference problem neutron cross section 两群单区问题的计算结果列于表2,本文计算的本征值为1.179 68,与MCNP参考解和TPHEX-A的计算结果很接近,另外快热中子通量比为7.05,也与参考解和TPHEX-A的一致。 表2 单区问题计算结果Table 2 One region benchmark problem result 两群两区问题的计算结果列于表3,本文计算的本征值为1.201 56,而MCNP参考解本征值为1.197 11,文献[10]中TPHEX-A计算的本征值为1.201 72,本文计算结果与TPHEX-A的基本一致。图3示出本文计算、TPHEX-A和MCNP参考解的各栅元快中子和热中子通量的分布,本文计算结果与MCNP和TPHEX-A的计算结果基本一致。图4示出MCNP计算的中子功率分布及本文方法和TPHEX-A计算的中子功率与参考解的相对偏差,可看出本文方法计算结果的平均相对偏差和最大相对偏差分别为1.0%和1.5%,本文方法计算的本征值和中子通量与MCNP结果符合良好,并与TPHEX-A计算结果的精度相当。 表3 两区问题计算结果Table 3 Two-region benchmark problem result 图3 参考问题快中子(a)和热中子(b)通量的分布Fig.3 Flux distribution of reference problem fast neutron (a) and thermal neutron (b) 离散纵标六角形节块法尽管相对差分格式离散纵标法有相当的计算效率优势,但由于输运方程的特点计算速度还是相对较慢。根据CMFD理论模型对离散纵标节块法采用了CMFD加速并进行了相应的数值模拟。 本文对上述两群两区参考问题进行计算,对于采用和不采用CMFD加速情况下离散纵标节块法的计算结果和外迭代次数进行了统计,结果列于表4。可看出,加速后的本征值和功率分布计算与不加速的结果是一致的,外迭代次数从不加速的近300次减少到不足20次,加速效果达到约16倍,离散纵标六角形CMFD加速取得了非常好的效果。 图4 参考问题栅元功率分布及其相对偏差Fig.4 Power distribution of reference problem and relative deviation 本文提出了一种中子平衡形式的离散纵标六角形节块法,数值结果表明,提出的模型是可行和正确的。此外,针对中子输运离散纵标法收敛较慢的问题,提出了针对六角形中子输运离散纵标法的CMFD方法,并取得了很好的效果。数值计算表明,对于参考问题CMFD可取得约16倍的加速效果。 为简便起见,本文采用栅元平源近似求解离散纵标六角形节块法来验证CMFD的加速性能,但为进一步提高计算精度,有必要在以后的研究中采用线性源甚至高阶源近似。 表4 CMFD加速效果Table 4 CMFD acceleration performance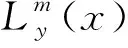



1.2 中子平衡方法

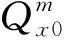

1.3 CMFD加速技术

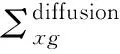
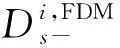
2 数值计算
2.1 参考问题
2.2 计算结果




2.3 CMFD加速性能

3 结论和展望


