层状TI介质中球面波的时域响应数值分析
张艳菊,巴振宁
(1.中国人民武装警察部队后勤学院后勤保障系,天津300309;2.天津大学 土木系,天津 300072;3.滨海土木工程结构与安全教育部重点实验室,天津 300072)
2002年朱传云等利用弹性球面波势函数进行了《爆炸应力波近似处理的分析与研究》[1]文中指出:爆炸时弹性球面波能否按平面波近似计算,其决定性影响因素是距离。一般当距离在2m~5m范围以外时,误差小于5%,弹性球面波即可近似按平面波处理,否则不能按平面波近似计算[1]。2004年国胜兵等基于有效应力动力分析法,对地下结构在竖向和水平爆炸地震波荷载作用下的动力响应进行数值分析[2];2005年朱波等利用波动有限元方法进行了钻地炸弹近爆地下工事动力响应数值分析,其本质仍然是利用波动方程,首先在空间域离散成各质点振动方程,然后将质点振动方程在时间域上离散成为代数方程求解[3]。2014年冯慧平等采用多物质流固耦合计算方法,对地下坑道对其临震塌爆距处钻地武器爆炸荷载的动力响应问题进行了研究[4]。但利用格林函数对爆炸波在TI介质中的动力响应规律的研究还较为少见。目前,Khojastech et al.(2008)[5,6]分别研究了TI全空间和半空间中的动力格林影响函数;Khojasteh et al.(2011)[7]采用传递矩阵方法研究了层状TI半空间的格林函数;Ai Zhiyong et.al(2014)[8]利用传递矩阵方法研究了对称荷载作用下二维层状TI半空间的动力响应问题;Chen(2015)[9]利用PIM方法研究了层状各向异性半空间中的三维格林影响函数。近年来,随着格林函数研究的不断完善,利用格林函数探索弹性波动力响应问题成为研究的热点,利用格林函数解决爆炸波在TI介质中的动力响应问题十分必要。目前,格林函数时域变化规律的研究还不够充分,因此,本文从格林函数时域数值结果入手,研究时域内格林函数在TI半空间和TI单一土层中随时间变化的规律,为研究爆炸波在层状TI介质中的动力响应问题奠定基础。本文利用频率-空间域内球面波在TI介质中的动力响应,通过傅里叶逆变换得到时域内的动力响应结果,并对时程结果进行计算分析得出有益结论。
1 模型与求解
本文的计算模型如图1所示,由N层TI土层和下卧基岩组成层状TI均匀半空间,每层土的材料特性由该层的质量密度、泊松比、模量等参数决定。各TI土层具体参数为:质量密度ρLj,竖向泊松比,水平泊松比,阻尼比ζLj,竖向弹性模量,水平弹性模量和竖向剪切模量,而水平剪切模量由土层水平弹性模量和泊松比即可确定为。复剪切模量、和每层土的厚度hj,(j=1…N );基岩参数包括质量密度ρR,竖向泊松比,水平泊松比,阻尼比ζR,竖向弹性模量,水平弹性模量,竖向剪切模量,水平剪切模量由基岩水平弹性模量和泊松比即可确定为。复剪切模量。图1中集中荷载作用位置为(0,0,zf),水平和竖向荷载大小分别为Fh和Fz。
在柱坐标系下,利用Lekhnistskii(1963)[10],Eskandari-Ghadi et al.(2005,2011)[11,12],Rahimian(2007)[13],Khojastech et al.(2008)[6]给出的柱坐标系下的解,建立反轴对称和轴对称刚度矩阵。推导出TI层状半空间的刚度矩阵,进而求解格林影响函数。而时域格林影响函数则可通过对频域结果的傅里叶逆变换求得。因此参照文献[6]的方法,求得空间域球面波作用下的位移和应力如公式(1)和(2)所示:
将公式(1)和(2)中球面波作用下的位移和应力动力响应,对时间进行傅里叶逆变换可得到时域内的计算结果,其逆变换具体形式如下:
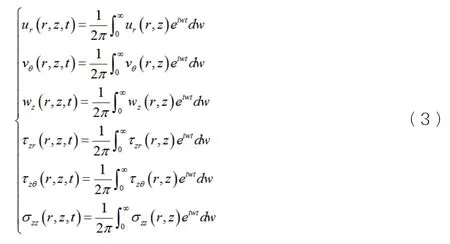
2 数值结果
以集中荷载分别作用于3种TI均匀半空间和基岩上3种单一TI土层为例进行数值计算分析。基岩和土层的计算参数如表1所示,基岩参数包括:质量密度ρR,水平泊松比,竖向泊松比,水平阻尼比,竖向阻尼比,水平弹性模量,竖向弹性模量,水平剪切模量和竖向剪切模量;表中土层参数包括:质量密度ρL,水平泊松比,竖向泊松比,水平阻尼比,竖向阻尼比,水平弹性模量,竖向弹性模量,水平剪切模量和竖向剪切模量,当所取土层与基岩参数相同时即为均匀半空间。zf为集中荷载埋置深度,土层厚度为h。频域计算中定义无量纲频率为η=ωd/c*,时域计算中定义无量纲频率为η=ωd/ 2πc*,为土层的竖向剪切波速。以下计算中:定义无量纲位移和应力为,其中d为无量纲单位长度。
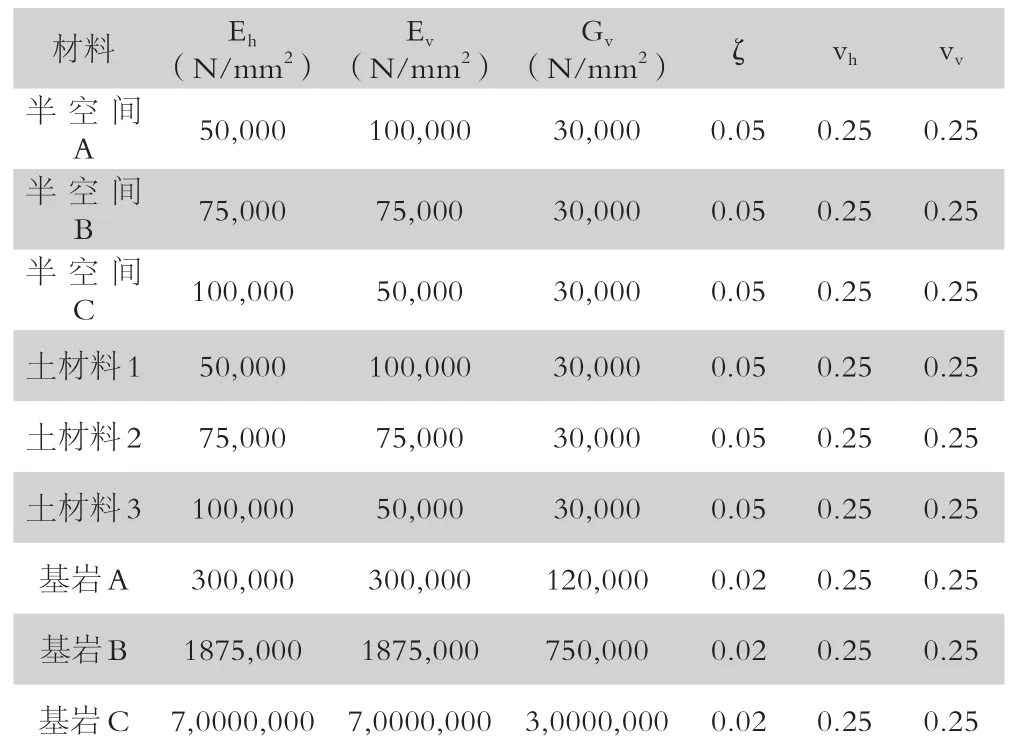
表1 模型的计算参数
2.1 格林影响函数时程曲线
图2首先给出了埋置荷载和计算面和计算点的位置图。模型参数如表1所示,以集中荷载分别作用于3种TI均匀半空间和基岩上3种单一TI土层为例,求解了水平和竖向简谐集中荷载分别作用时,4个不同位置观测点的动力格林影响函数。输入Ricker时程为特征频率定义为为土层的竖向剪切波速(均匀半空间情况为均匀半空间竖向剪切波速),土层厚度h=5d,集中荷载埋深zf=3d。时域动力响应通过对频域内动力响应的积分求得,计算时半空间情况采用表1中3种TI均匀半空间的参数,基岩上3种单一TI土层情况采用表1中基岩B和3种TI土层的参数,计算中无量纲频率计算范围为η=ωd/ 2πc*=0.0-6.0,采用分段高斯积分完成,共取积分频率点200个,无量纲时间τ=tc*/d=0-12。4个不同位置的观测点取自荷载下方zp=4d的水平面内,具体分布位置如图2(b)所示,其坐标分别为:A(d,d,4 d),B(3 d,d,4 d),C(d,3 d,4 d),D(3 d,3 d,4d)。无量纲位移无量纲应力。

图2 荷载和计算点布置图
图3和4首先给出了均匀半空间中分别作用水平和竖向简谐集中荷载时对应不同观测点的位移幅值时程和以及应力幅值时程,图中τ为无量纲时间。
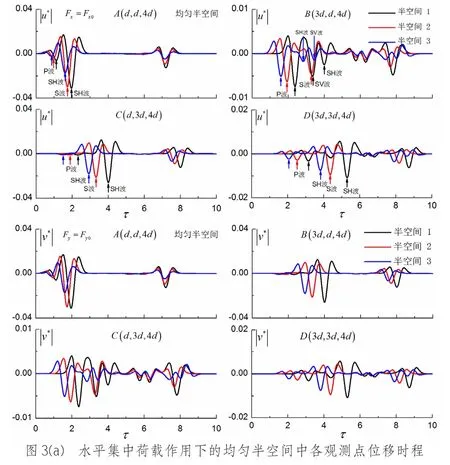

图3 集中荷载作用下的均匀半空间中各观测点位移时程
从图3中半空间的位移时程结果可以看出,各向同性介质(半空间2)与TI介质的位移时程有明显差别,且同一材料对应的各观测点位移时程也有显著差别。首先,从文献[14]的波速计算公式中可以看出,各向同性介质(半空间2)中P波和S波沿任意方向的传播速度是相同的,而TI介质中P波和S波的传播速度沿不同方向是不一样的,同时SV波与SH波的传播波速也不再相同,因此横波出现了分裂现象,即S波分裂成SV波与SH波,这一现象在B点的水平向位移的时程曲线和C点水平向位移的时程曲线图中表现的十分明显。其次,TI性质对位移时程有显著影响,随水平向模量(主要是Eh)的增大,水平激励产生的P、SV和SH波的传播速度增大,位移时程不断提前(波到的越早),位移幅值逐渐减小,且水平位移时程的差异较竖向位移的差异更显著。最后,TI介质具有对称性,对比同一介质的不同观测点位移时程发现,两观测点A和D的水平向位移与时程曲线相同;观测点B和C的竖向位移时程曲线相同;观测点B的水平位移与观测点C的水平位移时程曲线相同,反之亦然。
再者,比较图3(a)与图3(b)的结果发现,水平荷载激励产生波的传播速度与竖荷载激励产生波的传播速度不相同,随着水平模量(主要是Eh)的增大,水平荷载激励产生的横波的速度不断增大,横波到时逐渐提前,而竖向荷载激励产生的横波的速度略减小,横波到时略延迟。
最后,对水平荷载激励下直达波的到时进行计算并统计于表2中,我们发现:随水平向模量(主要是Eh)的增大,P、SV和SH波的传播速度逐渐增大,对应P、SV和SH波的到时也不断提前;且直接计算的结果(表2)与对频率进行傅里叶逆变换的结果(图3)十分吻合,进一步验证本文的正确性。


图4 集中荷载作用下的均匀半空间中各观测点应力时程
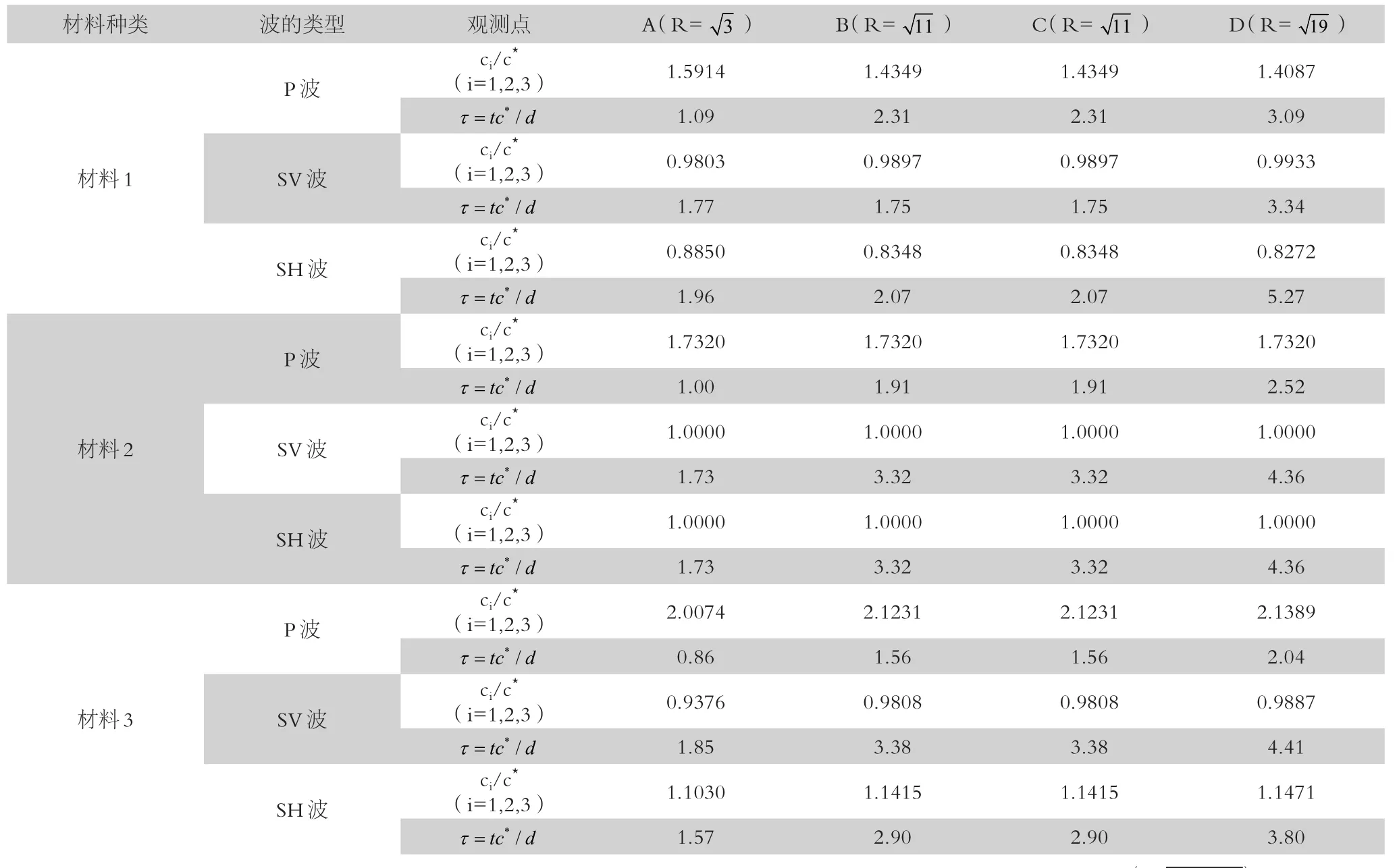
表2 三种Tl介质中波速与波的到时统计
从图4中半空间的应力时程结果可以看出与位移时程相类似的规律。各向同性介质(半空间2)与TI介质的应力时程有明显差别,且同一材料对应的各观测点应力时程也有显著差别。
TI性质对位移时程有显著影响。首先,在TI介质中波速受传播方向的影响,横波亦是出现了分裂现象,即S波分裂成SV波与SH波,这一现象在B点应力时程曲线和C点应力时程曲线图中表现的十分明显。其次,随水平向模量(主要是Eh)的增大,水平激励产生的P、SV和SH波的传播速度增大,波的到时不断提前(波到得越早),应力幅值逐渐减小,且剪应力时程的差异较正应力的差异更显著。另外,TI介质具有对称性,对比同一介质的不同观测点应力时程发现位与移时程类似的规律,观测点A和D的剪应力时程曲线相同;观测点B和C得正应力 时程曲线相同;观测点B的剪应力与观测点C的剪应力的时程曲线相同,反之亦然。


图5 集中荷载作用的基岩上单一TI土层中各观测点位移时程
图5给出了基岩上单一土层中分别作用水平和竖向简谐集中荷载时对应不同观测点的位移幅值时程u*、v*和。w*图5与均匀半空间图3的结果相比较,除了具有与半空间类似的规律外(①波速值随传播方向改变,②横波分裂,③TI介质对称性),TI土层的存在使位移和应力幅值都减小了。另外,由于基岩的存在,使得图5的位移时程曲线较均匀半空间情况更为复杂。不仅有荷载激励直接产生的P、SV和SH波,还有从土层与基岩交界面反射回来的反射P、SV和SH波,直达波与反射波的叠加使得结果更加复杂。
2.2 格林影响函数时域云图
仍以集中荷载分别作用于3种TI均匀半空间为例,求解水平和竖向简谐集中荷载分别作用时,在荷载下方zp=4d的水平面内,以原点(0,0,0)为圆心,r=5d为半径的圆盘内均匀取2601个计算点,图6和图7给出了集中荷载作用时,该圆盘内计算点在某些时刻τ的位移云图。输入Ricker时程为,特征频率定义为为半空间的竖向剪切波速,时域动力响应通过对频域内动力响应的积分求得。计算时采用表1中3种TI均匀半空间的参数,计算中无量纲频率计算范围为η=ωd/ 2πc*=0.0-6.0,共取积分频率点200个,采用分段高斯积分完成。
其次,位移幅值时域云图表现出了对称和反对称性质。比如,图6(a)水平荷载作用时的水平位移云图与7(b)竖向荷载作用时的竖向位移云图关于水平坐标轴(x、y轴)对称;图6(b)水平荷载作用时的竖向位移云图与图7(a)竖向荷载作用时的水平位移云图关于x坐标轴对称,关于y坐标轴反对称。

图6 水平集中荷载作用下位移云图

图7 竖向集中荷载作用下位移云图
最后,比较图6(a)与7(b)的云图发现,TI介质中水平荷载激励产生的波的速度与竖向荷载情况不同,随着水平模量的增大,水平荷载激励产生的波的速度不断增大,而竖向荷载激励产生的波的速度略减小,这正好解释了2.1节中,水平荷载作用下水平位移与竖向荷载作用下竖向位移时程中波的到时为何是不同[15]。
3 结论
本文根据TI介质中的波动方程利用Hankel积分变换和傅里叶级数展开求解出位移势函数,进而推导出TI层状场地反轴对称(SH)和轴对称(P-SV)精确动力刚度矩阵,然后利用直接刚度法进一步推导出TI层状介质中埋置集中荷载的动力格林影响函数公式,最后对频率进行傅里叶逆变换推导出时域的计算公式。文中以3种TI均匀半空间和基岩上3种TI单一土层中集中荷载作用下的格林函数为例,分别在频域和时域内进行了数值计算分析,得到了一下主要结论。
(1)TI均匀半空间中位移和应力的时程结果表明:首先,各向同性介质中P波和S波沿任意方向的传播速度是相同的,而TI介质中P波和S波的传播速度沿不同方向是同的,SV波与SH波的传播波速也不再相同,且横波出现了分裂现象,即S波分裂成SV波与SH波。其次,TI性质对位移时程有显著影响,随水平向模量(主要是Eh)的增大,水平激励产生的P、SV和SH波的传播速度增大,位移时程不断提前(波到的越早)。最后,TI介质具有对称性,对比同一介质的不同观测点位移时程发现,两观测点A和D的水平向位移和应力时程曲线相同;观测点B和C的竖向位移和应力时程曲线相同;观测点B的水平位移应力分别与观测点C的水平位移和应力时程曲线相同,反之亦然[16]。此外,水平荷载激励产生的波的传播速度与竖荷载激励产生的波的传播速度有差别,随着水平模量(主要是Eh)的增大,水平荷载激励产生的横波的速度不断增大,横波到时逐渐提前,而竖向荷载激励产生的横波的速度略减小,横波到时略延迟。
(2)TI土层的存在使基岩上单一TI土层情况的时程结果表明:除了具有与半空间类似的规律外(①波速值随传播方向改变,②横波分裂,③TI介质对称性),TI土层的存在使位移和应力幅值都减小,也使得位移和应力时程曲线较均匀半空间情况更为复杂。不仅有荷载激励直接产生的P、SV和SH波,还有从土层与基岩交界面反射回来的反射P、SV和SH波,直达波与反射波的叠加使得结果更加复杂[17]。
(3)时域内的位移幅值云图结果表明:首先,不同TI材料的介质中波的传播速度不同,各向同性介质中波沿各个方向的传播速度相同,在某一水平面上表现为波的传播是圆形扩散;同一TI半空间中(半空间2和3),波沿各个方向的传播速度不再相同,在某一水平面上表现为波的传播是圆形扩散。其次,TI半空间1在3.0时刻以及TI半空间3在2.0时刻的水平位移幅值云图均体现了S波分裂成SV波和SH波的现象。
其次,由于TI介质中SV波与SH波的传播速度不再相同,横波S波在TI半空间中分裂成了SV波和SH波,TI半空间1在3.0时刻以及TI半空间3在2.0时刻的水平位移幅值云图均体现了横波分裂现象,这也是与各向同性介质完全不同的一种特性[18]。以上这些规律与上2.1节位移时程规律一致。
最后,位移幅值时域云图表现出了对称和反对称性质。比如,图6(a)水平荷载作用时的水平位移云图与7(b)竖向荷载作用时的竖向位移云图关于水平坐标轴(x、y轴)对称;图6(b)水平荷载作用时的竖向位移云图与图7(a)竖向荷载作用时的水平位移云图关于x坐标轴对称,关于y坐标轴反对称。

